5.4二次函数的图像与性质(第3课时)课件
文档属性
| 名称 | 5.4二次函数的图像与性质(第3课时)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1023.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-25 00:00:00 | ||
图片预览






文档简介
课件20张PPT。5.4 二次函数的图象和性质
第3课时1.会画y=a(x-h)2+k的图象;
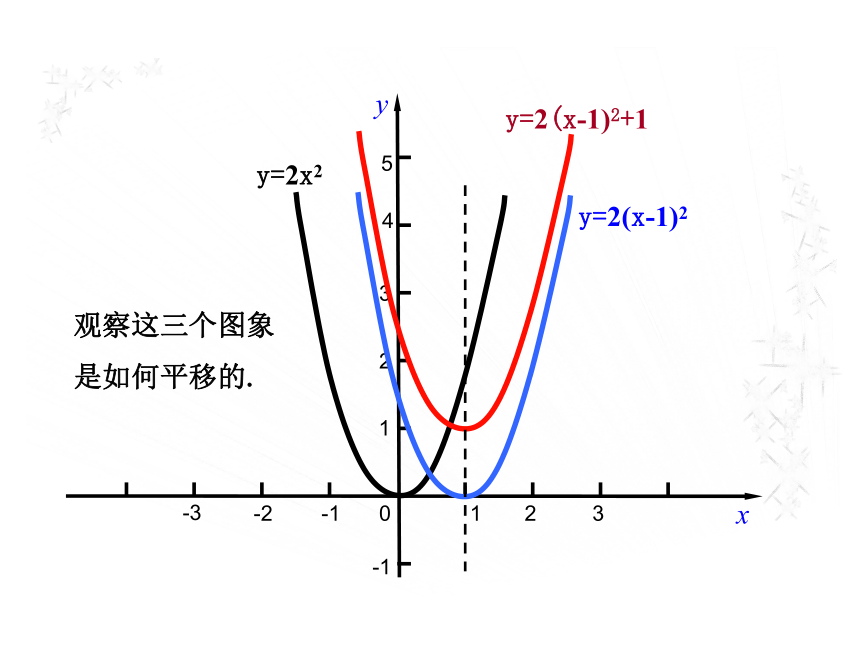
2.了解y=a(x-h)2+k的图象与y=ax2的关系,能结合图象理解 y=a(x-h)2+k的性质.观察图象,回答问题函数y=3(x-1)2的图象与y=3x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么? 在同一坐标系中作出二次函数y=3x2和 y=3(x-1)2的图象. 123-1-2-301234-1xy5y=2(x-1)2+1y=2(x-1)2 y=2x2观察这三个图象是如何平移的.二次函数y = ? x2,y = ? (x+1)2和y = ? (x+1)2?1的图
象有什么关系?它们的开口方向、对称轴和顶点坐标分别是
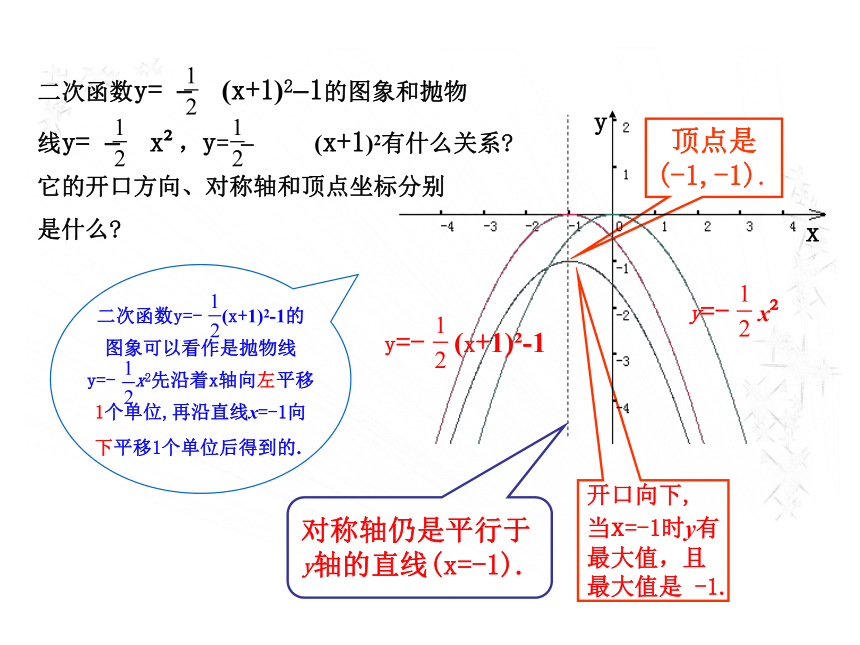
什么? 【例1】画出函数y=? (x+1)2?1的图象,指出它的开口方向、对称轴及顶点,抛物线y= ? x2经过怎样的变换可以得到抛物线y=- (x+1)2-1?思考:二次函数y=- (x+1)2-1的
图象可以看作是抛物线
y=- x2先沿着x轴向左平移
1个单位,再沿直线x=-1向
下平移1个单位后得到的.二次函数y= ? (x+1)2?1的图象和抛物
线y= ? x2,y= ? (x+1)2有什么关系?
它的开口方向、对称轴和顶点坐标分别
是什么?对称轴仍是平行于
y轴的直线(x=-1). 顶点是
(-1,-1).开口向下,
当x=-1时y有
最大值,且
最大值是 -1.y=- x2y=- (x+1)2-11.在同一坐标系中作出二次函数y=-3(x-1)2+2, y=-3(x-1)2-2,
y=-3x2和y=-3(x-1)2的图象.
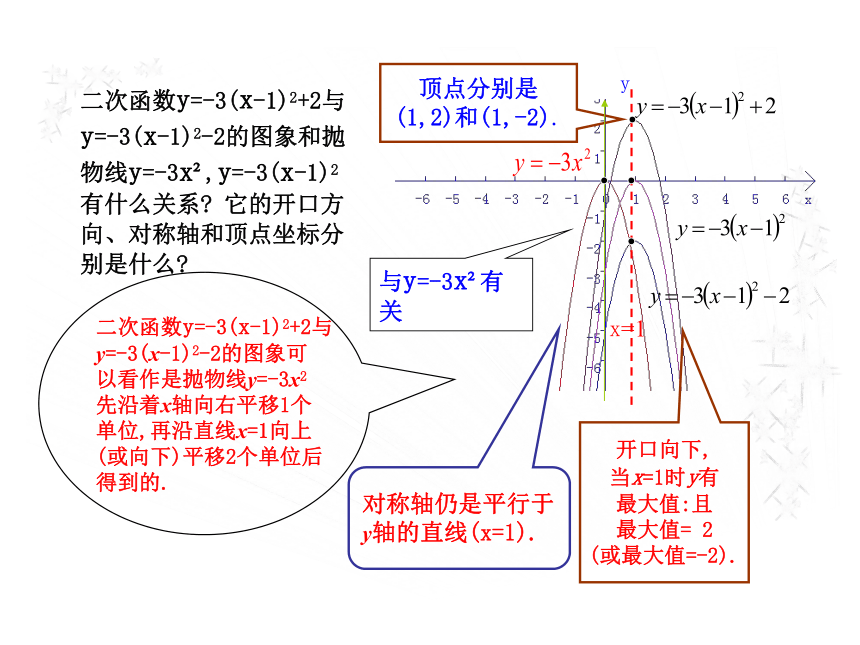
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2和y=-3x2,y=-3(x-1)2的图象有什么关系? 它是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小? 对称轴仍是平行于
y轴的直线(x=1). 顶点分别是
(1,2)和(1,-2).二次函数y=-3(x-1)2+2与
y=-3(x-1)2-2的图象可
以看作是抛物线y=-3x2
先沿着x轴向右平移1个
单位,再沿直线x=1向上
(或向下)平移2个单位后
得到的.开口向下,
当x=1时y有
最大值:且
最大值= 2
(或最大值=-2).yx=1与y=-3x2有关二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物线y=-3x2,y=-3(x-1)2有什么关系? 它的开口方向、对称轴和顶点坐标分别是什么?【规律方法】二次函数y=a(x-h)2+k与y=ax2的关系一般地,由y=ax2的图象便可得到二次函数y=a(x-h)2+k的图象.y=a(x-h)2+k(a≠0) 的图象可以看成y=ax2的图象先沿x轴整体向左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体向上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.
因此,二次函数y=a(x-h)2+k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标与a,h,k的值有关.
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时,开口向上;当a<0时,开口向下;
(2)对称轴是直线x=h;
(3)顶点坐标是(h,k).点(1,3)是顶点,知道h=1,k=3,求出a就可以了!yx【例 2】要修建一个圆形喷水池,在池中心竖立安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线型水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?点(3,0)在抛物线上,求a没问题.解析:如图建立直角坐标系,点(1,3)
是顶点,设抛物线的解析式为
y=a(x-1)2 +3(0≤x≤3),
∵点(3,0)在抛物线上,
∴0=a(3-1)2 +3,
∴a=-0.75,
∴y=-0.75(x-1)2 +3(0≤x≤3),
当x=0时,y=2.25,
即水管应长2.25m.1.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2?bx+c(a≠0).若此炮弹在第7秒与第14秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒B2.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅行团每增加一人,每人的单价就降低10元.当一个旅行团的人数是多少时,旅行社可以获得最大营业额?解析:设一个旅行团有x人时,旅行社营业额为y元.则
y=[800-10(x-30)]·x
=-10x2+1 100x=-10(x-55)2+30 250∴当x=55时,y最大=30 250答:一个旅行团有55人时,旅行社可获最大营业额30 250元1.如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为( )A.-3 B.1 C.5 D.8 【解析】选D.当C点横坐标最小时,抛物线顶点必为
A(1,4),根据此时抛物线的对称轴,可判断出
CD间的距离;当D点横坐标最大时,抛物线顶点为
B(4,4),再根据此时抛物线的对称轴及CD的长,
可判断出D点横坐标的最大值. 2.如图,两条抛物线y1= - x2+1、y2=- x2-1 与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为( )
A.8 B.6 C.10 D.4A3.某广场有一喷水池,水从地面喷出.如图,以水平地面为轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-(x-2)2+4(单位:米)的一部分,则水喷出的最大高度是( )
A.4米 B.3米 C.2米 D.1米【解析】选A. 抛物线的顶点坐标(2,4),
所以水喷出的最大高度
是4米.4.已知二次函数的图象如图所示,关于该函数在所给自变量取值范围内,下列说法正确的是( )
A.有最小值0,有最大值3
B.有最小值-1,有最大值0
C.有最小值-1,有最大值3
D.有最小值-1,无最大值
【解析】选C.因为图象顶点的纵
坐标为-1,最高值为3.故选C.5.把抛物线y=-x2先向上平移2个单位,再向右平移100个单位,那么所得抛物线与x轴的两个交点之间的距离是______【解析】先由平移规律求出新抛物线的解析式为y= -(x-100)2+2,然后求出抛物线与x轴的两个交点的横坐标,利用坐标轴上两点间距离公式即可求得距离. 答案:二次函数y=a(x-h)2+k的图象和性质再见
第3课时1.会画y=a(x-h)2+k的图象;
2.了解y=a(x-h)2+k的图象与y=ax2的关系,能结合图象理解 y=a(x-h)2+k的性质.观察图象,回答问题函数y=3(x-1)2的图象与y=3x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么? 在同一坐标系中作出二次函数y=3x2和 y=3(x-1)2的图象. 123-1-2-301234-1xy5y=2(x-1)2+1y=2(x-1)2 y=2x2观察这三个图象是如何平移的.二次函数y = ? x2,y = ? (x+1)2和y = ? (x+1)2?1的图
象有什么关系?它们的开口方向、对称轴和顶点坐标分别是
什么? 【例1】画出函数y=? (x+1)2?1的图象,指出它的开口方向、对称轴及顶点,抛物线y= ? x2经过怎样的变换可以得到抛物线y=- (x+1)2-1?思考:二次函数y=- (x+1)2-1的
图象可以看作是抛物线
y=- x2先沿着x轴向左平移
1个单位,再沿直线x=-1向
下平移1个单位后得到的.二次函数y= ? (x+1)2?1的图象和抛物
线y= ? x2,y= ? (x+1)2有什么关系?
它的开口方向、对称轴和顶点坐标分别
是什么?对称轴仍是平行于
y轴的直线(x=-1). 顶点是
(-1,-1).开口向下,
当x=-1时y有
最大值,且
最大值是 -1.y=- x2y=- (x+1)2-11.在同一坐标系中作出二次函数y=-3(x-1)2+2, y=-3(x-1)2-2,
y=-3x2和y=-3(x-1)2的图象.
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2和y=-3x2,y=-3(x-1)2的图象有什么关系? 它是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小? 对称轴仍是平行于
y轴的直线(x=1). 顶点分别是
(1,2)和(1,-2).二次函数y=-3(x-1)2+2与
y=-3(x-1)2-2的图象可
以看作是抛物线y=-3x2
先沿着x轴向右平移1个
单位,再沿直线x=1向上
(或向下)平移2个单位后
得到的.开口向下,
当x=1时y有
最大值:且
最大值= 2
(或最大值=-2).yx=1与y=-3x2有关二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物线y=-3x2,y=-3(x-1)2有什么关系? 它的开口方向、对称轴和顶点坐标分别是什么?【规律方法】二次函数y=a(x-h)2+k与y=ax2的关系一般地,由y=ax2的图象便可得到二次函数y=a(x-h)2+k的图象.y=a(x-h)2+k(a≠0) 的图象可以看成y=ax2的图象先沿x轴整体向左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体向上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.
因此,二次函数y=a(x-h)2+k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标与a,h,k的值有关.
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时,开口向上;当a<0时,开口向下;
(2)对称轴是直线x=h;
(3)顶点坐标是(h,k).点(1,3)是顶点,知道h=1,k=3,求出a就可以了!yx【例 2】要修建一个圆形喷水池,在池中心竖立安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线型水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?点(3,0)在抛物线上,求a没问题.解析:如图建立直角坐标系,点(1,3)
是顶点,设抛物线的解析式为
y=a(x-1)2 +3(0≤x≤3),
∵点(3,0)在抛物线上,
∴0=a(3-1)2 +3,
∴a=-0.75,
∴y=-0.75(x-1)2 +3(0≤x≤3),
当x=0时,y=2.25,
即水管应长2.25m.1.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2?bx+c(a≠0).若此炮弹在第7秒与第14秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒B2.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅行团每增加一人,每人的单价就降低10元.当一个旅行团的人数是多少时,旅行社可以获得最大营业额?解析:设一个旅行团有x人时,旅行社营业额为y元.则
y=[800-10(x-30)]·x
=-10x2+1 100x=-10(x-55)2+30 250∴当x=55时,y最大=30 250答:一个旅行团有55人时,旅行社可获最大营业额30 250元1.如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为( )A.-3 B.1 C.5 D.8 【解析】选D.当C点横坐标最小时,抛物线顶点必为
A(1,4),根据此时抛物线的对称轴,可判断出
CD间的距离;当D点横坐标最大时,抛物线顶点为
B(4,4),再根据此时抛物线的对称轴及CD的长,
可判断出D点横坐标的最大值. 2.如图,两条抛物线y1= - x2+1、y2=- x2-1 与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为( )
A.8 B.6 C.10 D.4A3.某广场有一喷水池,水从地面喷出.如图,以水平地面为轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-(x-2)2+4(单位:米)的一部分,则水喷出的最大高度是( )
A.4米 B.3米 C.2米 D.1米【解析】选A. 抛物线的顶点坐标(2,4),
所以水喷出的最大高度
是4米.4.已知二次函数的图象如图所示,关于该函数在所给自变量取值范围内,下列说法正确的是( )
A.有最小值0,有最大值3
B.有最小值-1,有最大值0
C.有最小值-1,有最大值3
D.有最小值-1,无最大值
【解析】选C.因为图象顶点的纵
坐标为-1,最高值为3.故选C.5.把抛物线y=-x2先向上平移2个单位,再向右平移100个单位,那么所得抛物线与x轴的两个交点之间的距离是______【解析】先由平移规律求出新抛物线的解析式为y= -(x-100)2+2,然后求出抛物线与x轴的两个交点的横坐标,利用坐标轴上两点间距离公式即可求得距离. 答案:二次函数y=a(x-h)2+k的图象和性质再见
