第4章 等可能条件下的概率 单元训练2023-2024学年苏科版数学九年级上册(含解析)
文档属性
| 名称 | 第4章 等可能条件下的概率 单元训练2023-2024学年苏科版数学九年级上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 327.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 21:47:26 | ||
图片预览



文档简介
第4章 等可能条件下的概率 单元训练——苏科版数学九年级上
一、选择题
1.抛一枚均匀的骰子,下列事件中,发生可能性最大的是( )
A.点数是奇数 B.点数是3的倍数
C.点数大于5 D.点数小于5
2.下列事件中,属于必然事件的是( )
A.射击运动员射击一次,命中10 环
B.有一匹马奔跑的速度是70米/秒
C.任意抛掷一只纸杯,杯口朝下
D.在地面上向空中抛掷一石块,石块终将落下
3.在四张完全相同的卡片上,分别画有圆、菱形、等边三角形、等腰梯形,现从中随机抽取一张,卡片上的图形恰好是中心对称图形的概率是( )
A. B. C. D.1
4.对于两个事件:
事件:任意掷一枚质地均匀的正方体骰子,掷出的点数是小于;
事件:口袋中有除颜色外其他都完全相同的个红球和个白球,从中摸出个球,其中至少一个是红球:
有如下说法,其中正确的是( )
A.事件、均为必然事件
B.事件、均为随机事件
C.事件是随机事件,事件是必然事件
D.事件是必然事件,事件是随机事件
5.按小王、小李、小马三位同学的顺序从一个不透明的盒子中随机抽取一张标注“主持人”和两张空白的纸条,确定一位同学主持班级“交通安全教有”主题班会.下列说法中正确的是( )
A.小王的可能性最大 B.小李的可能性最大
C.小马的可能性最大 D.三人的可能性一样大
6.一个不透明布袋里有四个完全相同的小球,把它们分别标号为1,2,3,5,从中任意摸出一个球,记下编号后放回,搅匀,再任意摸出一个球,则两次摸出的球的编号之和为偶数的概率是( )
A. B. C. D.
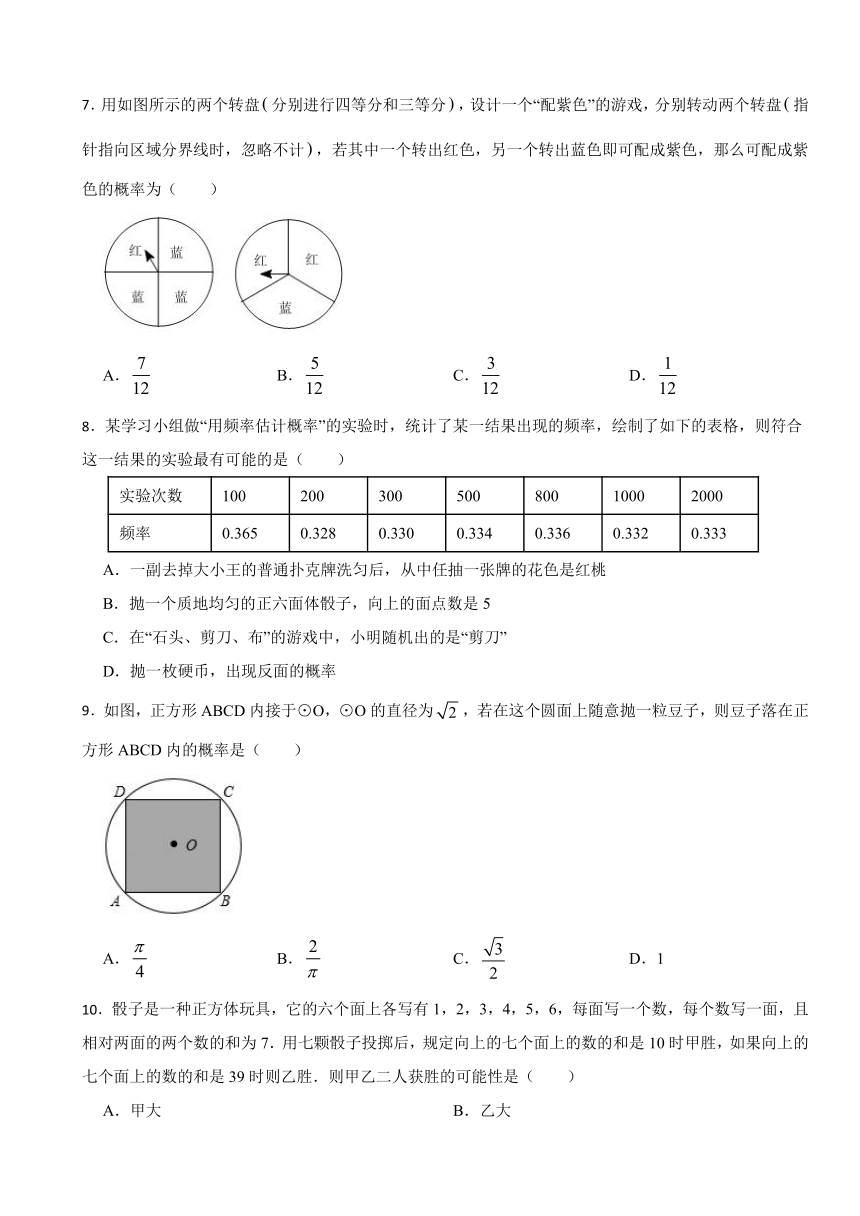
7.用如图所示的两个转盘分别进行四等分和三等分,设计一个“配紫色”的游戏,分别转动两个转盘指针指向区域分界线时,忽略不计,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率为( )
A. B. C. D.
8.某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 100 200 300 500 800 1000 2000
频率 0.365 0.328 0.330 0.334 0.336 0.332 0.333
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.抛一个质地均匀的正六面体骰子,向上的面点数是5
C.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
D.抛一枚硬币,出现反面的概率
9.如图,正方形ABCD内接于⊙O,⊙O的直径为,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
A. B. C. D.1
10.骰子是一种正方体玩具,它的六个面上各写有1,2,3,4,5,6,每面写一个数,每个数写一面,且相对两面的两个数的和为7.用七颗骰子投掷后,规定向上的七个面上的数的和是10时甲胜,如果向上的七个面上的数的和是39时则乙胜.则甲乙二人获胜的可能性是( )
A.甲大 B.乙大
C.同样大 D.无法确定谁大
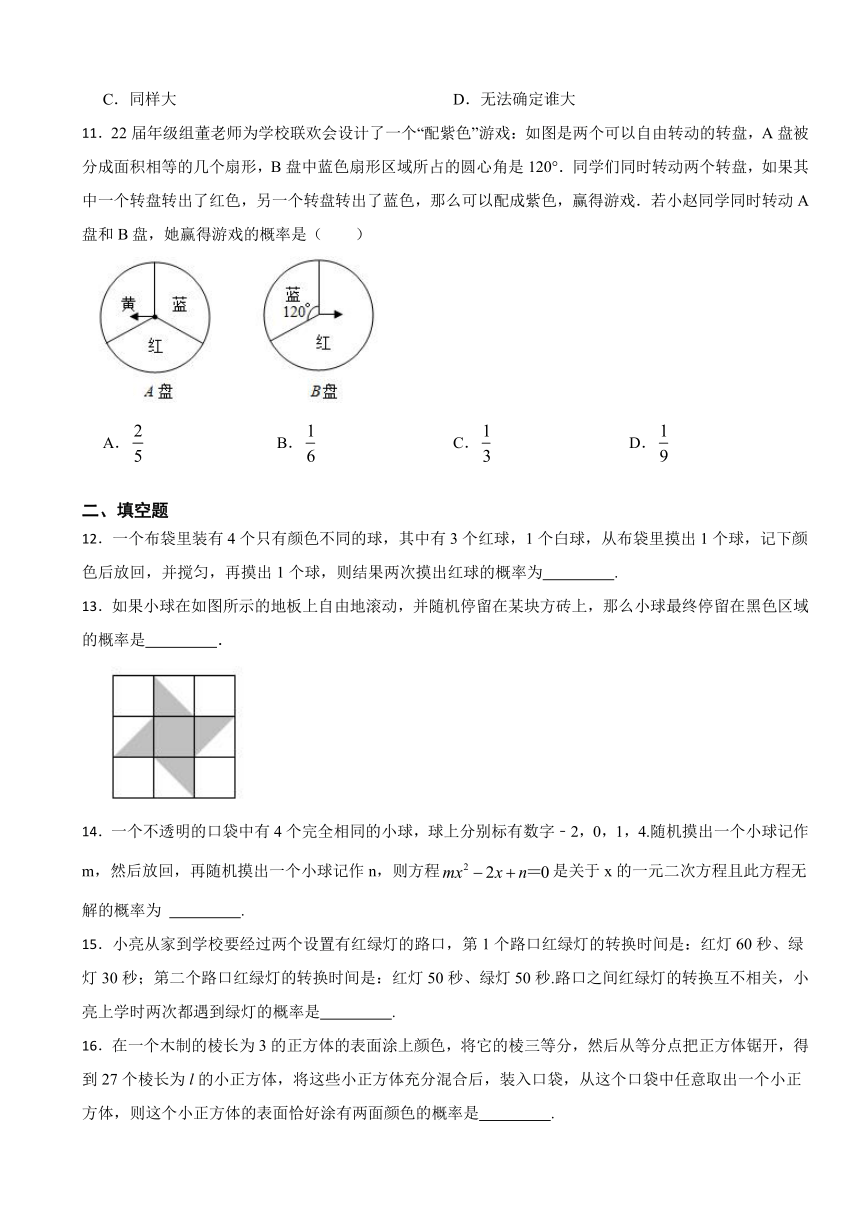
11.22届年级组董老师为学校联欢会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,A盘被分成面积相等的几个扇形,B盘中蓝色扇形区域所占的圆心角是120°.同学们同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色,赢得游戏.若小赵同学同时转动A盘和B盘,她赢得游戏的概率是( )
A. B. C. D.
二、填空题
12.一个布袋里装有4个只有颜色不同的球,其中有3个红球,1个白球,从布袋里摸出1个球,记下颜色后放回,并搅匀,再摸出1个球,则结果两次摸出红球的概率为 .
13.如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,那么小球最终停留在黑色区域的概率是 .
14.一个不透明的口袋中有4个完全相同的小球,球上分别标有数字﹣2,0,1,4.随机摸出一个小球记作m,然后放回,再随机摸出一个小球记作n,则方程是关于x的一元二次方程且此方程无解的概率为 .
15.小亮从家到学校要经过两个设置有红绿灯的路口,第1个路口红绿灯的转换时间是:红灯60秒、绿灯30秒;第二个路口红绿灯的转换时间是:红灯50秒、绿灯50秒.路口之间红绿灯的转换互不相关,小亮上学时两次都遇到绿灯的概率是 .
16.在一个木制的棱长为3的正方体的表面涂上颜色,将它的棱三等分,然后从等分点把正方体锯开,得到27个棱长为l的小正方体,将这些小正方体充分混合后,装入口袋,从这个口袋中任意取出一个小正方体,则这个小正方体的表面恰好涂有两面颜色的概率是 .
三、解答题
17.在一不透明的袋子中装有四张标有数字2,3,4,5的卡片,这些卡片除数字外其余均相同.小明同学按照一定的规则抽出两张卡片,并把卡片上的数字相加,下图是他所画的树状图的一部分.
(1)由上图分析,该游戏规则是:第一次从袋子中随机抽出一张卡片后 (填“放回”或“不放回”),第二次随机再抽出一张卡片;
(2)帮小明同学补全树状图,并求小明同学两次抽到卡片上的数字之和为偶数的概率.
18.某商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定:顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准打折区域顾客就可以获得此项待遇(转盘等分成8份,指针停在每个区域的机会相等).
(1)甲顾客消费150元,求获得打折待遇的概率;
(2)乙顾客消费120元,求获得五折待遇的概率.
19.一个不透明的袋中装有个白球,个黑球,个红球,每个球除颜色外都相同.
(1)从中任意摸出一个球,摸到红球是 事件;摸到黄球是事件 ;填“不可能”或“必然”或“随机”
(2)从中任意摸出一个球,摸到黑球的概率;
(3)现在再将若干个同样的黑球放入袋中、与原来个球均匀混合在一起,使从袋中任意摸出一个球为黑球的概率为,请求出后来放入袋中的黑球个数.
20.如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).
(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD面上的概率为 ,若存在,指出其中的一种平移方式;若不存在,请说明理?
答案解析部分
1.【答案】D
【解析】解:掷一枚质地均匀的骰子,骰子停止后共有6种等可能的情况,
即:点数为1,2,3,4,5,6;其中点数是奇数的有3种,点数是3的倍数的有2种,点数大于5的有1种,点数小于5的有4种,
故点数小于5的可能性较大.
故答案为:D.
2.【答案】D
【解析】解:A、射击运动员射击一次,可能命中10环,也可能不会命中10环,故是随机事件,不符合题意;
B、有一匹马奔跑的速度是70米每秒,是不可能事件,不符合题意;
C、任意抛掷一只纸杯,杯口朝下,是随机事件,不符合题意;
D、在地面上向空中抛掷一石块,石块受地球引力的作用,石块终将落下,是必然事件,符合题意.
故答案为:D.
3.【答案】A
【解析】解:∵圆、菱形是中心对称图形,
∴从中随机抽取一张,卡片上的图形恰好是中心对称图形的概率为=;
故答案为:A.
4.【答案】C
【解析】解:事件1:任意掷一枚质地均匀的正方体骰子,掷出的点数是小于6,属于随机事件;
事件2:口袋中有除颜色外其他都完全相同的2个红球和1个白球,从中摸出2个球,其中至少一个是红球,属于必然事件.
故答案为:C.
5.【答案】D
【解析】解:小王先抽,小王可能抽到“主持人”,也可能抽到空白纸条,则分为两种情况:
小王抽到“主持人”可能性为,
小王抽到空白纸条的可能性为:,在此基础上,小李抽取情况分为抽到“主持人”或抽到空白纸条,
抽取“主持人”可能性为:,
抽取空白纸条可能性为:(当此种情况出现时,则小李必抽到“主持人”),
故小李抽到“主持人”的可能性为:,
小马抽到“主持人”的可能性为:,
故答案为:D.
6.【答案】D
【解析】解:画树状图如下:
共有16种等情况数,其中两次摸出的球的编号之和为偶数的情况有10种,
∴两次摸出的球的编号之和为偶数的概率是=.
故答案为:D.
7.【答案】A
【解析】解:第一个转盘转出红色的概率为,转出蓝色的概率为,第二个转盘转出红色的概率为,转出蓝色的概率为,然后根据红色与蓝色可配成紫色可得:配成紫色的概率为×+×=.
故答案为:A.
8.【答案】C
【解析】解:A、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率为,不符合题意;
B、抛一个质地均匀的正六面体骰子,向上的面点数是5的概率为,不符合题意;
C、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率是,符合题意;
D、抛一枚硬币,出现反面的概率为,不符合题意,
故答案为:C.
9.【答案】B
【解析】解:由题得 ,
如上图,由勾股定理可得,
豆子落在正方形ABCD内的概率 .
故答案为:B.
10.【答案】C
【解析】解:向上的七个面上的数的和是10的情况有:
1,1,1,1,1,1,4
1,1,1,1,1,2,3
1,1,1,1,2,2,2
向上的七个面上的数的和是39的情况有:
6,6,6,6,6,6,3
6,6,6,6,6,5,4
6,6,6,6,5,5,5
∴共有6种情况,其中和为10的有3中情况,和为39的有3中情况.
∴P(向上的七个面上的数的和是10)=P(向上的七个面上的数的和是39)= ,
∴P(向上的七个面上的数的和是10)=P(向上的七个面上的数的和是39).
故选C.
11.【答案】C
【解析】解:∵B盘中蓝色扇形区域所占的圆心角为120°,
∴B盘红色扇形区域所占的圆心角为240°,
∴B盘中:S红色扇形=2S蓝色扇形,
画树状图如下:
∴一共有9种等可能的结果,其中一个转盘转出了红色、另一个转盘转出了蓝色的有3种情况,
∴小赵同学同时转动A盘和B盘,她赢得游戏的概率是=.
故答案为:C.
12.【答案】
【解析】解:画树状图如图:
共有16种等可能的情况,其中两次摸到的球都是红球的有9种情况,
∴两次摸到的球都是红球的概率为.
故答案为:.
13.【答案】
【解析】解:∵由图可知,黑色方砖有块,共有块方砖,
∴黑色方砖在整个地板中所占的比值,
∴小球最终停留在黑色区域的概率是,
故答案为:.
14.【答案】
【解析】解:∵一元二次方程无实数根,
,且,
即,且,
,且,
画树状图如下:
由此知,共有16种等可能结果,其中且的有4种结果,
所以方程是关于x的一元二次方程且此方程无解的概率为.
故答案为:.
15.【答案】
【解析】解:∵第1个路口红灯60秒、绿灯30秒,
∴第1个路口可以看作2红1绿,
∵第2个路口红灯50秒、绿灯50秒,
∴第2个路口看作1红1绿,
画出树状图,如图所示:
∵共有6种等可能的情况,两个路口都遇到绿灯的情况数为1种,
∴小亮上学时两次都遇到绿灯的概率为.
16.【答案】
【解析】解:∵在27个小正方体中,恰好有三个面都涂色有颜色的共有8个,恰好有两个都涂有颜色的共12个,恰好有一个面都涂有颜色的共6个,表面没涂颜色的1个.
∴恰好涂有两面颜色的概率是 .
故答案为:
17.【答案】(1)不放回
(2)解:如图:
由树状图可知,共有 种可能出现的结果,并且它们是等可能的.
事件“甲同学两次抽到的数字之和为偶数”的发生有 种可能,
所以它的概率 .
18.【答案】(1)解:∵转盘等分成8份,有5个打折的区域,
∴甲顾客消费150元,获得打折待遇的概率为;
(2)解:∵转盘等分成8份,有2个打五折的区域,
∴乙顾客消费120元,获得五折待遇的概率为.
19.【答案】(1)随机;不可能
(2)解:,
故摸到黑球的概率是;
(3)解:设后来放入袋中的黑球的个数是个,依题意有:
,
解得.
答:后来放入袋中的黑球的个数为个.
【解析】解:(1)∵在一个不透明的袋中装有2个白球、3个黑球和5个红球,每个球除颜色外都相同,
∴任意摸出一球,摸到红球是随机事件,摸到黄球是不可能事件;
故答案为:随机,不可能;
20.【答案】(1)解:依题可得,
由表格可知构成点P的坐标共有16种等可能性的结果,其中(1,1),(1,2),(2,1),(2,2),这4种情况落在正方形ABCD面上,
∴ P点落在正方形ABCD面上(含正方形内部和边界)的概率P=.
答: P点落在正方形ABCD面上(含正方形内部和边界)的概率为.
(2)解:∵使点P落在正方形ABCD面上的概率为=>,
∴只能将正方形ABCD向上或向右整数个单位平移,且使点P落在正方形面上的数目为12,
∴存在这样的平移:先将正方形ABCD向上平移2个单位,再向右平移1个单位.
一、选择题
1.抛一枚均匀的骰子,下列事件中,发生可能性最大的是( )
A.点数是奇数 B.点数是3的倍数
C.点数大于5 D.点数小于5
2.下列事件中,属于必然事件的是( )
A.射击运动员射击一次,命中10 环
B.有一匹马奔跑的速度是70米/秒
C.任意抛掷一只纸杯,杯口朝下
D.在地面上向空中抛掷一石块,石块终将落下
3.在四张完全相同的卡片上,分别画有圆、菱形、等边三角形、等腰梯形,现从中随机抽取一张,卡片上的图形恰好是中心对称图形的概率是( )
A. B. C. D.1
4.对于两个事件:
事件:任意掷一枚质地均匀的正方体骰子,掷出的点数是小于;
事件:口袋中有除颜色外其他都完全相同的个红球和个白球,从中摸出个球,其中至少一个是红球:
有如下说法,其中正确的是( )
A.事件、均为必然事件
B.事件、均为随机事件
C.事件是随机事件,事件是必然事件
D.事件是必然事件,事件是随机事件
5.按小王、小李、小马三位同学的顺序从一个不透明的盒子中随机抽取一张标注“主持人”和两张空白的纸条,确定一位同学主持班级“交通安全教有”主题班会.下列说法中正确的是( )
A.小王的可能性最大 B.小李的可能性最大
C.小马的可能性最大 D.三人的可能性一样大
6.一个不透明布袋里有四个完全相同的小球,把它们分别标号为1,2,3,5,从中任意摸出一个球,记下编号后放回,搅匀,再任意摸出一个球,则两次摸出的球的编号之和为偶数的概率是( )
A. B. C. D.
7.用如图所示的两个转盘分别进行四等分和三等分,设计一个“配紫色”的游戏,分别转动两个转盘指针指向区域分界线时,忽略不计,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率为( )
A. B. C. D.
8.某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 100 200 300 500 800 1000 2000
频率 0.365 0.328 0.330 0.334 0.336 0.332 0.333
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.抛一个质地均匀的正六面体骰子,向上的面点数是5
C.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
D.抛一枚硬币,出现反面的概率
9.如图,正方形ABCD内接于⊙O,⊙O的直径为,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
A. B. C. D.1
10.骰子是一种正方体玩具,它的六个面上各写有1,2,3,4,5,6,每面写一个数,每个数写一面,且相对两面的两个数的和为7.用七颗骰子投掷后,规定向上的七个面上的数的和是10时甲胜,如果向上的七个面上的数的和是39时则乙胜.则甲乙二人获胜的可能性是( )
A.甲大 B.乙大
C.同样大 D.无法确定谁大
11.22届年级组董老师为学校联欢会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,A盘被分成面积相等的几个扇形,B盘中蓝色扇形区域所占的圆心角是120°.同学们同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色,赢得游戏.若小赵同学同时转动A盘和B盘,她赢得游戏的概率是( )
A. B. C. D.
二、填空题
12.一个布袋里装有4个只有颜色不同的球,其中有3个红球,1个白球,从布袋里摸出1个球,记下颜色后放回,并搅匀,再摸出1个球,则结果两次摸出红球的概率为 .
13.如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,那么小球最终停留在黑色区域的概率是 .
14.一个不透明的口袋中有4个完全相同的小球,球上分别标有数字﹣2,0,1,4.随机摸出一个小球记作m,然后放回,再随机摸出一个小球记作n,则方程是关于x的一元二次方程且此方程无解的概率为 .
15.小亮从家到学校要经过两个设置有红绿灯的路口,第1个路口红绿灯的转换时间是:红灯60秒、绿灯30秒;第二个路口红绿灯的转换时间是:红灯50秒、绿灯50秒.路口之间红绿灯的转换互不相关,小亮上学时两次都遇到绿灯的概率是 .
16.在一个木制的棱长为3的正方体的表面涂上颜色,将它的棱三等分,然后从等分点把正方体锯开,得到27个棱长为l的小正方体,将这些小正方体充分混合后,装入口袋,从这个口袋中任意取出一个小正方体,则这个小正方体的表面恰好涂有两面颜色的概率是 .
三、解答题
17.在一不透明的袋子中装有四张标有数字2,3,4,5的卡片,这些卡片除数字外其余均相同.小明同学按照一定的规则抽出两张卡片,并把卡片上的数字相加,下图是他所画的树状图的一部分.
(1)由上图分析,该游戏规则是:第一次从袋子中随机抽出一张卡片后 (填“放回”或“不放回”),第二次随机再抽出一张卡片;
(2)帮小明同学补全树状图,并求小明同学两次抽到卡片上的数字之和为偶数的概率.
18.某商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定:顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准打折区域顾客就可以获得此项待遇(转盘等分成8份,指针停在每个区域的机会相等).
(1)甲顾客消费150元,求获得打折待遇的概率;
(2)乙顾客消费120元,求获得五折待遇的概率.
19.一个不透明的袋中装有个白球,个黑球,个红球,每个球除颜色外都相同.
(1)从中任意摸出一个球,摸到红球是 事件;摸到黄球是事件 ;填“不可能”或“必然”或“随机”
(2)从中任意摸出一个球,摸到黑球的概率;
(3)现在再将若干个同样的黑球放入袋中、与原来个球均匀混合在一起,使从袋中任意摸出一个球为黑球的概率为,请求出后来放入袋中的黑球个数.
20.如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).
(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD面上的概率为 ,若存在,指出其中的一种平移方式;若不存在,请说明理?
答案解析部分
1.【答案】D
【解析】解:掷一枚质地均匀的骰子,骰子停止后共有6种等可能的情况,
即:点数为1,2,3,4,5,6;其中点数是奇数的有3种,点数是3的倍数的有2种,点数大于5的有1种,点数小于5的有4种,
故点数小于5的可能性较大.
故答案为:D.
2.【答案】D
【解析】解:A、射击运动员射击一次,可能命中10环,也可能不会命中10环,故是随机事件,不符合题意;
B、有一匹马奔跑的速度是70米每秒,是不可能事件,不符合题意;
C、任意抛掷一只纸杯,杯口朝下,是随机事件,不符合题意;
D、在地面上向空中抛掷一石块,石块受地球引力的作用,石块终将落下,是必然事件,符合题意.
故答案为:D.
3.【答案】A
【解析】解:∵圆、菱形是中心对称图形,
∴从中随机抽取一张,卡片上的图形恰好是中心对称图形的概率为=;
故答案为:A.
4.【答案】C
【解析】解:事件1:任意掷一枚质地均匀的正方体骰子,掷出的点数是小于6,属于随机事件;
事件2:口袋中有除颜色外其他都完全相同的2个红球和1个白球,从中摸出2个球,其中至少一个是红球,属于必然事件.
故答案为:C.
5.【答案】D
【解析】解:小王先抽,小王可能抽到“主持人”,也可能抽到空白纸条,则分为两种情况:
小王抽到“主持人”可能性为,
小王抽到空白纸条的可能性为:,在此基础上,小李抽取情况分为抽到“主持人”或抽到空白纸条,
抽取“主持人”可能性为:,
抽取空白纸条可能性为:(当此种情况出现时,则小李必抽到“主持人”),
故小李抽到“主持人”的可能性为:,
小马抽到“主持人”的可能性为:,
故答案为:D.
6.【答案】D
【解析】解:画树状图如下:
共有16种等情况数,其中两次摸出的球的编号之和为偶数的情况有10种,
∴两次摸出的球的编号之和为偶数的概率是=.
故答案为:D.
7.【答案】A
【解析】解:第一个转盘转出红色的概率为,转出蓝色的概率为,第二个转盘转出红色的概率为,转出蓝色的概率为,然后根据红色与蓝色可配成紫色可得:配成紫色的概率为×+×=.
故答案为:A.
8.【答案】C
【解析】解:A、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃的概率为,不符合题意;
B、抛一个质地均匀的正六面体骰子,向上的面点数是5的概率为,不符合题意;
C、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率是,符合题意;
D、抛一枚硬币,出现反面的概率为,不符合题意,
故答案为:C.
9.【答案】B
【解析】解:由题得 ,
如上图,由勾股定理可得,
豆子落在正方形ABCD内的概率 .
故答案为:B.
10.【答案】C
【解析】解:向上的七个面上的数的和是10的情况有:
1,1,1,1,1,1,4
1,1,1,1,1,2,3
1,1,1,1,2,2,2
向上的七个面上的数的和是39的情况有:
6,6,6,6,6,6,3
6,6,6,6,6,5,4
6,6,6,6,5,5,5
∴共有6种情况,其中和为10的有3中情况,和为39的有3中情况.
∴P(向上的七个面上的数的和是10)=P(向上的七个面上的数的和是39)= ,
∴P(向上的七个面上的数的和是10)=P(向上的七个面上的数的和是39).
故选C.
11.【答案】C
【解析】解:∵B盘中蓝色扇形区域所占的圆心角为120°,
∴B盘红色扇形区域所占的圆心角为240°,
∴B盘中:S红色扇形=2S蓝色扇形,
画树状图如下:
∴一共有9种等可能的结果,其中一个转盘转出了红色、另一个转盘转出了蓝色的有3种情况,
∴小赵同学同时转动A盘和B盘,她赢得游戏的概率是=.
故答案为:C.
12.【答案】
【解析】解:画树状图如图:
共有16种等可能的情况,其中两次摸到的球都是红球的有9种情况,
∴两次摸到的球都是红球的概率为.
故答案为:.
13.【答案】
【解析】解:∵由图可知,黑色方砖有块,共有块方砖,
∴黑色方砖在整个地板中所占的比值,
∴小球最终停留在黑色区域的概率是,
故答案为:.
14.【答案】
【解析】解:∵一元二次方程无实数根,
,且,
即,且,
,且,
画树状图如下:
由此知,共有16种等可能结果,其中且的有4种结果,
所以方程是关于x的一元二次方程且此方程无解的概率为.
故答案为:.
15.【答案】
【解析】解:∵第1个路口红灯60秒、绿灯30秒,
∴第1个路口可以看作2红1绿,
∵第2个路口红灯50秒、绿灯50秒,
∴第2个路口看作1红1绿,
画出树状图,如图所示:
∵共有6种等可能的情况,两个路口都遇到绿灯的情况数为1种,
∴小亮上学时两次都遇到绿灯的概率为.
16.【答案】
【解析】解:∵在27个小正方体中,恰好有三个面都涂色有颜色的共有8个,恰好有两个都涂有颜色的共12个,恰好有一个面都涂有颜色的共6个,表面没涂颜色的1个.
∴恰好涂有两面颜色的概率是 .
故答案为:
17.【答案】(1)不放回
(2)解:如图:
由树状图可知,共有 种可能出现的结果,并且它们是等可能的.
事件“甲同学两次抽到的数字之和为偶数”的发生有 种可能,
所以它的概率 .
18.【答案】(1)解:∵转盘等分成8份,有5个打折的区域,
∴甲顾客消费150元,获得打折待遇的概率为;
(2)解:∵转盘等分成8份,有2个打五折的区域,
∴乙顾客消费120元,获得五折待遇的概率为.
19.【答案】(1)随机;不可能
(2)解:,
故摸到黑球的概率是;
(3)解:设后来放入袋中的黑球的个数是个,依题意有:
,
解得.
答:后来放入袋中的黑球的个数为个.
【解析】解:(1)∵在一个不透明的袋中装有2个白球、3个黑球和5个红球,每个球除颜色外都相同,
∴任意摸出一球,摸到红球是随机事件,摸到黄球是不可能事件;
故答案为:随机,不可能;
20.【答案】(1)解:依题可得,
由表格可知构成点P的坐标共有16种等可能性的结果,其中(1,1),(1,2),(2,1),(2,2),这4种情况落在正方形ABCD面上,
∴ P点落在正方形ABCD面上(含正方形内部和边界)的概率P=.
答: P点落在正方形ABCD面上(含正方形内部和边界)的概率为.
(2)解:∵使点P落在正方形ABCD面上的概率为=>,
∴只能将正方形ABCD向上或向右整数个单位平移,且使点P落在正方形面上的数目为12,
∴存在这样的平移:先将正方形ABCD向上平移2个单位,再向右平移1个单位.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
