第2章 对称图形—圆 单元训练2023-2024学年苏科版数学九年级上册(含解析)
文档属性
| 名称 | 第2章 对称图形—圆 单元训练2023-2024学年苏科版数学九年级上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 21:48:59 | ||
图片预览




文档简介
第2章 对称图形—圆 单元训练——苏科版数学九年级上
一、选择题
1.下列图形为圆的是( )
A. B. C. D.
2.已知是半径为2的圆的一条弦,则的长可能是( )
A.4 B.5 C.6 D.7
3.下列说法:(1)长度相等的弧是等弧,(2)相等的圆心角所对的弧相等,(3)劣弧一定比优弧短,(4)直径是圆中最长的弦.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.若的半径为,点P到圆心O的距离,则点P的位置是( )
A.在内 B.在上 C.在外 D.不能确定
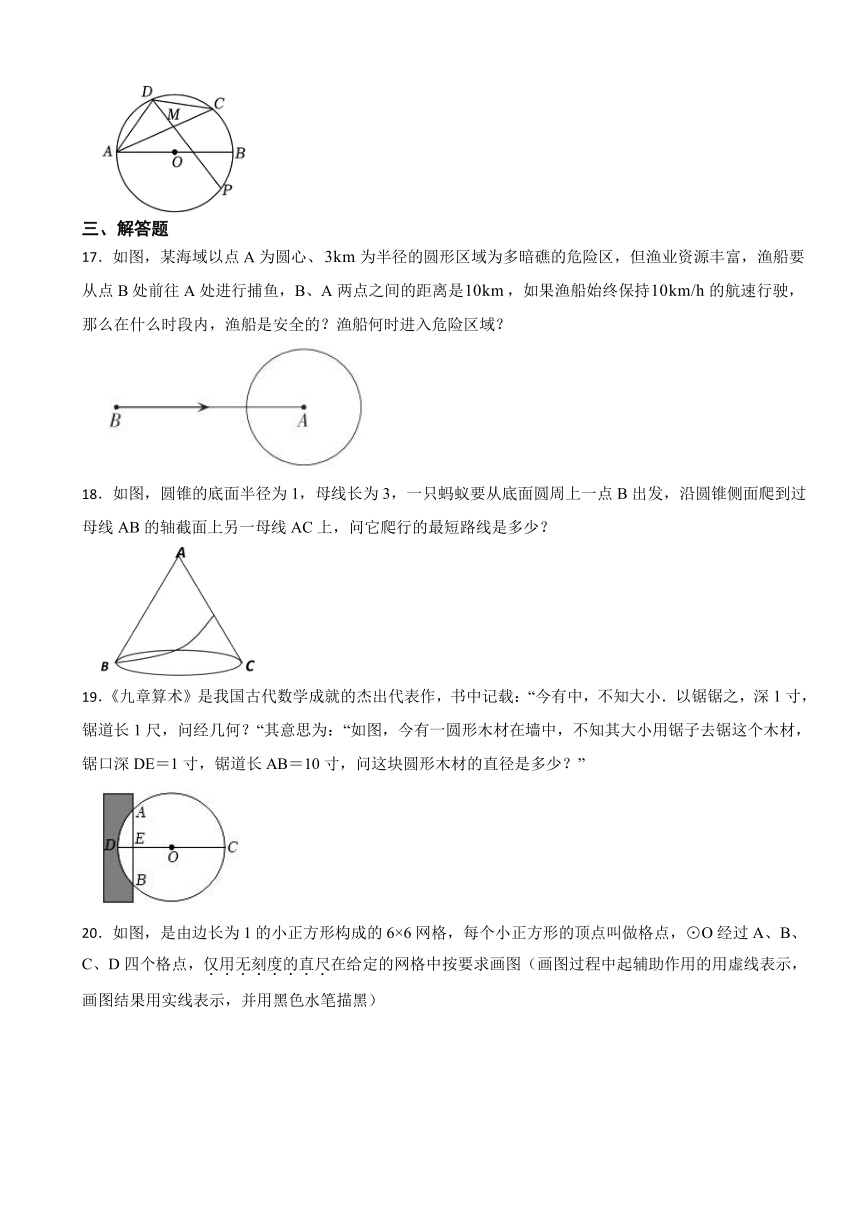
5.如图,已知是的一条弦,,点M在上,且,若,则⊙O的半径为( )
A.4 B.5 C.6 D.
6.直角三角形的外心在( )
A.直角顶点 B.直角三角形内
C.直角三角形外 D.斜边中点
7.如图,在中,,,,点D在边上,,以点D为圆心作,其半径长为r,要使点A恰在外,点B在内,则r的取值范围是( )
A. B. C. D.
8.如图,,为的两条弦,、分别为,的中点,的半径为若,则的长为( )
A. B. C. D.
9.如图,PA、PC是⊙O的两条切线,点A、C为切点,点B为⊙O上任意一点,连接AB、BC,若∠B=52°,则∠P的度数为( ).
A.68° B.104° C.70° D.76°
10.如图,五边形是⊙O的内接正五边形,则的度数为( )
A. B. C. D.
11.如图,点A,B,C在上,,连接,.若的半径为3,则扇形(阴影部分)的面积为( )
A. B. C. D.
12.如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=5,CD=2.以A为圆心,AD为半径的圆与BC边相切于点M,与AB交于点E,将扇形A﹣DME剪下围成一个圆锥,则圆锥的高为( )
A.1 B.4 C. D.
二、填空题
13.⊙O中,弦AB的长恰等于半径,则弧的度数是 度.
14.如图1,我国是世界上最早制造使用水车的国家.1556年兰州人段续的第一架水车创制成功后,黄河两岸人民纷纷仿制,车水灌田,水渠纵横,沃土繁丰.而今,兰州水车博览园是百里黄河风情线上的标志性景观,是兰州“水车之都”的象征.如图2是水车舀水灌溉示意图,水车轮的辐条(圆的半径)长约为6米,辐条尽头装有刮板,刮板间安装有等距斜挂的长方体形状的水斗,当水流冲动水车轮刮板时,驱使水车徐徐转动,水斗依次舀满河水在点处离开水面,逆时针旋转上升至轮子上方处,斗口开始翻转向下,将水倾入木槽,由木槽导入水渠,进而灌溉,那么水斗从处(舀水)转动到处(倒水)所经过的路程是 米.(结果保留)
15.如图,是半径为2的的弦,将沿着弦折叠,正好经过圆心O,点C是折叠后的上一动点,连接并延长交于点D,点E是的中点,连接,.则的最小值为 .
16.如图,是的直径,,两点在圆上,连接,,且,,为上一动点,在运动过程中,与相交于点,当为等腰三角形时,的度数为 .
三、解答题
17.如图,某海域以点A为圆心、为半径的圆形区域为多暗礁的危险区,但渔业资源丰富,渔船要从点B处前往A处进行捕鱼,B、A两点之间的距离是,如果渔船始终保持的航速行驶,那么在什么时段内,渔船是安全的?渔船何时进入危险区域?
18.如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?
19.《九章算术》是我国古代数学成就的杰出代表作,书中记载:“今有中,不知大小.以锯锯之,深1寸,锯道长1尺,问经几何?“其意思为:“如图,今有一圆形木材在墙中,不知其大小用锯子去锯这个木材,锯口深DE=1寸,锯道长AB=10寸,问这块圆形木材的直径是多少?”
20.如图,是由边长为1的小正方形构成的6×6网格,每个小正方形的顶点叫做格点,⊙O经过A、B、C、D四个格点,仅用无刻度的直尺在给定的网格中按要求画图(画图过程中起辅助作用的用虚线表示,画图结果用实线表示,并用黑色水笔描黑)
(1)如图1,判断圆心O (填“是”或“不是”)在格点上,并在图1中标出格点O;
(2)在图1中画出⊙O的切线CG(G为格点);
(3)在图2中画出的中点E;
21.如图,是⊙O的直径,点A在⊙O上且平分弧,于点,分别交,于,.
(1)求证:;
(2)若,求阴影部分面积.
答案解析部分
1.【答案】A
【解析】解:A,此图形是圆,故A符合题意;
B、此图形不是圆,故B不符合题意;
C、此图形不是圆,故C不符合题意;
D、此图形是扇形,故D不符合题意;
故答案为:A.
2.【答案】A
【解析】解:∵圆的半径为2,
∴圆的直径为4,
∵是半径为2的圆的一条弦,
∴,
故答案为:A.
3.【答案】A
【解析】解:(1) 长度相等的弧不一定是等弧,长度相等且度数也相同的弧才是等弧,故(1)错误;
(2)同圆或等圆中相等的圆心角所对的弧相等,故(2)错误;
(3)同圆或等圆中劣弧一定比优弧短,故(3)错误;
(4)直径是圆中最长的弦,故(4)正确,
综上正确的只有1个.
故答案为:A.
4.【答案】C
【解析】解:∵圆O的半径为6cm,点P到圆心O的距离PO=8cm,6<8,
∴点P在圆O外,
故答案为:C.
5.【答案】B
【解析】解:如图,过点O作OH⊥AB于点H,连接OB,
∵OH⊥AB,AB=6,
∴AH=BH=3,
∵AM=2,
∴MH=AH-AM=1,
在Rt△HMO中,由勾股定理得OH=4,
在Rt△HBO中,利用勾股定理可得OB=5,即⊙O的半径为5.
故答案为:B.
6.【答案】D
【解析】解:∵三角形的外心为三角形三边垂直平分线的交点,
∴直角三角形的外心在斜边中点.
故答案为:D.
7.【答案】A
【解析】解:在中,,,,
则,,
点A恰在外,点B在内,
故答案为:A.
8.【答案】D
【解析】解:如图,连接AB、OA、OB,
∵∠C=45°,
∴∠AOB=2∠C=90°,
在Rt△AOB中,∠AOB=90°,OA=OB=2,
∴AB=,
∵点D、G分别是AC与BC的中点,
∴DG=AB=.
故答案为:D.
9.【答案】D
【解析】解:如图,连接OA,OC,
∵PA、PB 是⊙O的两条切线,点A、C为切点,
∴∠PAO=∠PCO=90°,
∵∠B=52°,
∴∠AOC=2∠B=104°,
∴∠P=360°-90°-90°-104°=76°.
故答案为:D.
10.【答案】D
【解析】解:∵五边形是⊙O的内接正五边形,
∴∠A=∠ABC=,AB=AE,
∴∠ABE=∠AEB,
∴∠ABE=,
∴.
故答案为:D.
11.【答案】D
【解析】解:∵∠ABC=40°,
∴∠AOC=2∠ABC=80°,
∴S扇形AOC=.
故答案为:D.
12.【答案】C
【解析】解:如图,作CF⊥AB于F,连接AM.
∵AD∥CF,CD∥AF,
∴四边形ADCF是平行四边形,
∴∠A=90°,
∴四边形ADCF是矩形,
∴AD=CF=AM,CD=AF=2,
∵AB=5,∴BF=3,
在△AMB和△CFB中,
,
∴△AMB≌△CFB,
∴BM=BF=3,
在Rt△AMB中,AM= = =4,
设圆锥的高为h,底面半径为r,
由题意2π r= 2π 4,
∴r=1,
∴h= = ,
故选C.
13.【答案】60
【解析】解:如图,连接OA,OB,
∵OA=OB=AB,∴△ABC是等边三角形,∴∠AOB=60°,∴的度数为60°;
故答案为:60.
14.【答案】
【解析】解:由题意得:弧AB的长为=5π(米);
故答案为:5π.
15.【答案】
【解析】 如图,连接AE和EF,
∵△ACD是等边三角形,E是CD中点
∴AE⊥BD(三线合一)
又∵OF⊥AB
∴F是AB中点
即,EF是△ABE斜边中线
∴AF=EF=BF
即,E点在以AB为直径的圆上运动.
所以,当E、O、F在同一直线时,OE长度最小
此时,AE=EF,AE⊥EF
∵圆O的半径是2,即OA=2,OF=1
∴AF=(勾股定理)
∴OE=EF-OF=AF-OF=.
16.【答案】40°或70°或100°
【解析】解:连接,
,,
,
,
是的直径,
,
,
,
,
,
当为等腰三角形时,
①当时,,
②当时,,
③当时,,
故答案为:40°或70°或100°
17.【答案】解:如图,
∵,
∴,
由,
知到之间,渔船是安全的;渔船进入危险区域
18.【答案】解:如图,沿过母线AB的轴截面展开得扇形 ,
此时弧 的长为底面圆周长的一半,故 ,
由 , ,则 ,
作 ,此时 即为蚂蚁爬行的最短路径,
在 中, .
19.【答案】解:如图,连接OA,由题意可知,DE=1寸,AB=10寸,
∵AB⊥CD,CD是直径,AB=10寸,
∴AE=BE= AB=5(寸),
设圆O的半径OA的长为x寸,则OC=OD=x寸,
∵DE=1寸,
∴OE=(x﹣1)寸,
在Rt△AOE中,根据勾股定理得,
OA2﹣OE2=AE2,
即x2﹣(x﹣1)2=52,
解得:x=13(寸)
所以CD=26(寸).
答:这块圆形木材的直径为26寸.
20.【答案】(1)解:是.
(2)解:如图,即为所求.
(3)解:如图,即为所求.
【解析】解:(1)点O为圆心,且在格点上,理由如下:
如图, ⊙O经过A、B、C、D四个格点,
∵OC=OD=
∴点O为圆心,此时点O在格点上.
故答案为:是.
21.【答案】(1)证明:∵A点平分弧
弧=弧,
.
∵是⊙O的直径,
.
,
.
(2)解:连接AO、EO、EC,作EH⊥BC于H ,
.
又
是等边三角形,
.
∵弧=弧,
.
∵OE=OC
是等边三角形,
一、选择题
1.下列图形为圆的是( )
A. B. C. D.
2.已知是半径为2的圆的一条弦,则的长可能是( )
A.4 B.5 C.6 D.7
3.下列说法:(1)长度相等的弧是等弧,(2)相等的圆心角所对的弧相等,(3)劣弧一定比优弧短,(4)直径是圆中最长的弦.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.若的半径为,点P到圆心O的距离,则点P的位置是( )
A.在内 B.在上 C.在外 D.不能确定
5.如图,已知是的一条弦,,点M在上,且,若,则⊙O的半径为( )
A.4 B.5 C.6 D.
6.直角三角形的外心在( )
A.直角顶点 B.直角三角形内
C.直角三角形外 D.斜边中点
7.如图,在中,,,,点D在边上,,以点D为圆心作,其半径长为r,要使点A恰在外,点B在内,则r的取值范围是( )
A. B. C. D.
8.如图,,为的两条弦,、分别为,的中点,的半径为若,则的长为( )
A. B. C. D.
9.如图,PA、PC是⊙O的两条切线,点A、C为切点,点B为⊙O上任意一点,连接AB、BC,若∠B=52°,则∠P的度数为( ).
A.68° B.104° C.70° D.76°
10.如图,五边形是⊙O的内接正五边形,则的度数为( )
A. B. C. D.
11.如图,点A,B,C在上,,连接,.若的半径为3,则扇形(阴影部分)的面积为( )
A. B. C. D.
12.如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=5,CD=2.以A为圆心,AD为半径的圆与BC边相切于点M,与AB交于点E,将扇形A﹣DME剪下围成一个圆锥,则圆锥的高为( )
A.1 B.4 C. D.
二、填空题
13.⊙O中,弦AB的长恰等于半径,则弧的度数是 度.
14.如图1,我国是世界上最早制造使用水车的国家.1556年兰州人段续的第一架水车创制成功后,黄河两岸人民纷纷仿制,车水灌田,水渠纵横,沃土繁丰.而今,兰州水车博览园是百里黄河风情线上的标志性景观,是兰州“水车之都”的象征.如图2是水车舀水灌溉示意图,水车轮的辐条(圆的半径)长约为6米,辐条尽头装有刮板,刮板间安装有等距斜挂的长方体形状的水斗,当水流冲动水车轮刮板时,驱使水车徐徐转动,水斗依次舀满河水在点处离开水面,逆时针旋转上升至轮子上方处,斗口开始翻转向下,将水倾入木槽,由木槽导入水渠,进而灌溉,那么水斗从处(舀水)转动到处(倒水)所经过的路程是 米.(结果保留)
15.如图,是半径为2的的弦,将沿着弦折叠,正好经过圆心O,点C是折叠后的上一动点,连接并延长交于点D,点E是的中点,连接,.则的最小值为 .
16.如图,是的直径,,两点在圆上,连接,,且,,为上一动点,在运动过程中,与相交于点,当为等腰三角形时,的度数为 .
三、解答题
17.如图,某海域以点A为圆心、为半径的圆形区域为多暗礁的危险区,但渔业资源丰富,渔船要从点B处前往A处进行捕鱼,B、A两点之间的距离是,如果渔船始终保持的航速行驶,那么在什么时段内,渔船是安全的?渔船何时进入危险区域?
18.如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?
19.《九章算术》是我国古代数学成就的杰出代表作,书中记载:“今有中,不知大小.以锯锯之,深1寸,锯道长1尺,问经几何?“其意思为:“如图,今有一圆形木材在墙中,不知其大小用锯子去锯这个木材,锯口深DE=1寸,锯道长AB=10寸,问这块圆形木材的直径是多少?”
20.如图,是由边长为1的小正方形构成的6×6网格,每个小正方形的顶点叫做格点,⊙O经过A、B、C、D四个格点,仅用无刻度的直尺在给定的网格中按要求画图(画图过程中起辅助作用的用虚线表示,画图结果用实线表示,并用黑色水笔描黑)
(1)如图1,判断圆心O (填“是”或“不是”)在格点上,并在图1中标出格点O;
(2)在图1中画出⊙O的切线CG(G为格点);
(3)在图2中画出的中点E;
21.如图,是⊙O的直径,点A在⊙O上且平分弧,于点,分别交,于,.
(1)求证:;
(2)若,求阴影部分面积.
答案解析部分
1.【答案】A
【解析】解:A,此图形是圆,故A符合题意;
B、此图形不是圆,故B不符合题意;
C、此图形不是圆,故C不符合题意;
D、此图形是扇形,故D不符合题意;
故答案为:A.
2.【答案】A
【解析】解:∵圆的半径为2,
∴圆的直径为4,
∵是半径为2的圆的一条弦,
∴,
故答案为:A.
3.【答案】A
【解析】解:(1) 长度相等的弧不一定是等弧,长度相等且度数也相同的弧才是等弧,故(1)错误;
(2)同圆或等圆中相等的圆心角所对的弧相等,故(2)错误;
(3)同圆或等圆中劣弧一定比优弧短,故(3)错误;
(4)直径是圆中最长的弦,故(4)正确,
综上正确的只有1个.
故答案为:A.
4.【答案】C
【解析】解:∵圆O的半径为6cm,点P到圆心O的距离PO=8cm,6<8,
∴点P在圆O外,
故答案为:C.
5.【答案】B
【解析】解:如图,过点O作OH⊥AB于点H,连接OB,
∵OH⊥AB,AB=6,
∴AH=BH=3,
∵AM=2,
∴MH=AH-AM=1,
在Rt△HMO中,由勾股定理得OH=4,
在Rt△HBO中,利用勾股定理可得OB=5,即⊙O的半径为5.
故答案为:B.
6.【答案】D
【解析】解:∵三角形的外心为三角形三边垂直平分线的交点,
∴直角三角形的外心在斜边中点.
故答案为:D.
7.【答案】A
【解析】解:在中,,,,
则,,
点A恰在外,点B在内,
故答案为:A.
8.【答案】D
【解析】解:如图,连接AB、OA、OB,
∵∠C=45°,
∴∠AOB=2∠C=90°,
在Rt△AOB中,∠AOB=90°,OA=OB=2,
∴AB=,
∵点D、G分别是AC与BC的中点,
∴DG=AB=.
故答案为:D.
9.【答案】D
【解析】解:如图,连接OA,OC,
∵PA、PB 是⊙O的两条切线,点A、C为切点,
∴∠PAO=∠PCO=90°,
∵∠B=52°,
∴∠AOC=2∠B=104°,
∴∠P=360°-90°-90°-104°=76°.
故答案为:D.
10.【答案】D
【解析】解:∵五边形是⊙O的内接正五边形,
∴∠A=∠ABC=,AB=AE,
∴∠ABE=∠AEB,
∴∠ABE=,
∴.
故答案为:D.
11.【答案】D
【解析】解:∵∠ABC=40°,
∴∠AOC=2∠ABC=80°,
∴S扇形AOC=.
故答案为:D.
12.【答案】C
【解析】解:如图,作CF⊥AB于F,连接AM.
∵AD∥CF,CD∥AF,
∴四边形ADCF是平行四边形,
∴∠A=90°,
∴四边形ADCF是矩形,
∴AD=CF=AM,CD=AF=2,
∵AB=5,∴BF=3,
在△AMB和△CFB中,
,
∴△AMB≌△CFB,
∴BM=BF=3,
在Rt△AMB中,AM= = =4,
设圆锥的高为h,底面半径为r,
由题意2π r= 2π 4,
∴r=1,
∴h= = ,
故选C.
13.【答案】60
【解析】解:如图,连接OA,OB,
∵OA=OB=AB,∴△ABC是等边三角形,∴∠AOB=60°,∴的度数为60°;
故答案为:60.
14.【答案】
【解析】解:由题意得:弧AB的长为=5π(米);
故答案为:5π.
15.【答案】
【解析】 如图,连接AE和EF,
∵△ACD是等边三角形,E是CD中点
∴AE⊥BD(三线合一)
又∵OF⊥AB
∴F是AB中点
即,EF是△ABE斜边中线
∴AF=EF=BF
即,E点在以AB为直径的圆上运动.
所以,当E、O、F在同一直线时,OE长度最小
此时,AE=EF,AE⊥EF
∵圆O的半径是2,即OA=2,OF=1
∴AF=(勾股定理)
∴OE=EF-OF=AF-OF=.
16.【答案】40°或70°或100°
【解析】解:连接,
,,
,
,
是的直径,
,
,
,
,
,
当为等腰三角形时,
①当时,,
②当时,,
③当时,,
故答案为:40°或70°或100°
17.【答案】解:如图,
∵,
∴,
由,
知到之间,渔船是安全的;渔船进入危险区域
18.【答案】解:如图,沿过母线AB的轴截面展开得扇形 ,
此时弧 的长为底面圆周长的一半,故 ,
由 , ,则 ,
作 ,此时 即为蚂蚁爬行的最短路径,
在 中, .
19.【答案】解:如图,连接OA,由题意可知,DE=1寸,AB=10寸,
∵AB⊥CD,CD是直径,AB=10寸,
∴AE=BE= AB=5(寸),
设圆O的半径OA的长为x寸,则OC=OD=x寸,
∵DE=1寸,
∴OE=(x﹣1)寸,
在Rt△AOE中,根据勾股定理得,
OA2﹣OE2=AE2,
即x2﹣(x﹣1)2=52,
解得:x=13(寸)
所以CD=26(寸).
答:这块圆形木材的直径为26寸.
20.【答案】(1)解:是.
(2)解:如图,即为所求.
(3)解:如图,即为所求.
【解析】解:(1)点O为圆心,且在格点上,理由如下:
如图, ⊙O经过A、B、C、D四个格点,
∵OC=OD=
∴点O为圆心,此时点O在格点上.
故答案为:是.
21.【答案】(1)证明:∵A点平分弧
弧=弧,
.
∵是⊙O的直径,
.
,
.
(2)解:连接AO、EO、EC,作EH⊥BC于H ,
.
又
是等边三角形,
.
∵弧=弧,
.
∵OE=OC
是等边三角形,
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
