11.1.1 三角形的边 教案 2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 11.1.1 三角形的边 教案 2023-2024学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 00:00:00 | ||
图片预览


文档简介
课题11.1.1 三角形的边
素养目标:
1.结合具体的实例,进一步认识三角形的概念及其基本要素.
2.会用符号、字母表示三角形,并能按边的相等关系对三角形进行分类.
3.理解三角形两边之和大于第三边与两边之差小于第三边的性质,并会初步运用这些性质解决问题.
4.会用数学的语言描述三角形的三边关系.
一.教学目标:
1.知识与技能:(1)认识三角形并会用几何语言表示三角形,了解三角形分类.
(2)掌握三角形的三边关系. (3)运用三角形三边关系解决有关的问题
2.过程与方法:通过回顾小学已学过的知识,以学生为中心进一步学习三角形的相关知识,体现学生的主体地位;
3.情感与态度:在利用所学知识进行解题的过程中,培养学生学习数学的兴趣和探究的能力。
二.教学重、难点:
重点:认识三角形的边,内角,顶点,能用符号语言表示三角形。
难点:运用三角形三边的不等关系解决生活实际问题。
教学方法:指导---自主学习
教学准备:课件,三角尺
教学过程设计
1.温故知新
问题1:我们一起来回顾:一条线可以成为哪些几何图形?
问题2:增加一条线,两条线可以组成哪些已学过的几何图形
问题3:老师再增加一条线,三条线又可以组成哪些几何图形
2.情境引入
出示著名建筑、金字塔、战机、大桥等图片,让学生感受生活中的三角形,体会生活中处处有数学.教师利用多媒体演示三角形的形成过程,让学生观察.
思考:(1)从古埃及的金字塔到现代的飞机,从宏伟的建筑物到微小的分子结构,都有什么样的形象?(2)在我们的生活中有没有这样的形象呢?试举例.
3.新知学习
问题1:在小学我们已经初步学习了三角形的有关知识,请同学们根据小学所学的知识,说一说你对三角形有哪些认识?学生小组交流并展示汇报。
问题2:从各组汇报展示结果来看,大家主要从哪些方面来研究三角形?
师归纳:从定义、分类、性质三方面研究三角形,也是我们研究几何图形的一般思路。
1.定义:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
线段AB,BC,CA是三角形的边. 点A,B,C是三角形的顶点. ∠A,∠B,∠C是相邻两边组成的角,叫做三角形的内角,简称三角形的角.
顶点是A,B,C的三角形,记作△ABC,读作“三角形ABC”.
△ABC的三边,有时也用a,b,c来表示. 顶点A所对的边BC用a表示,顶点B所对的边AC用b表示,顶点C所对的边AB用c表示.
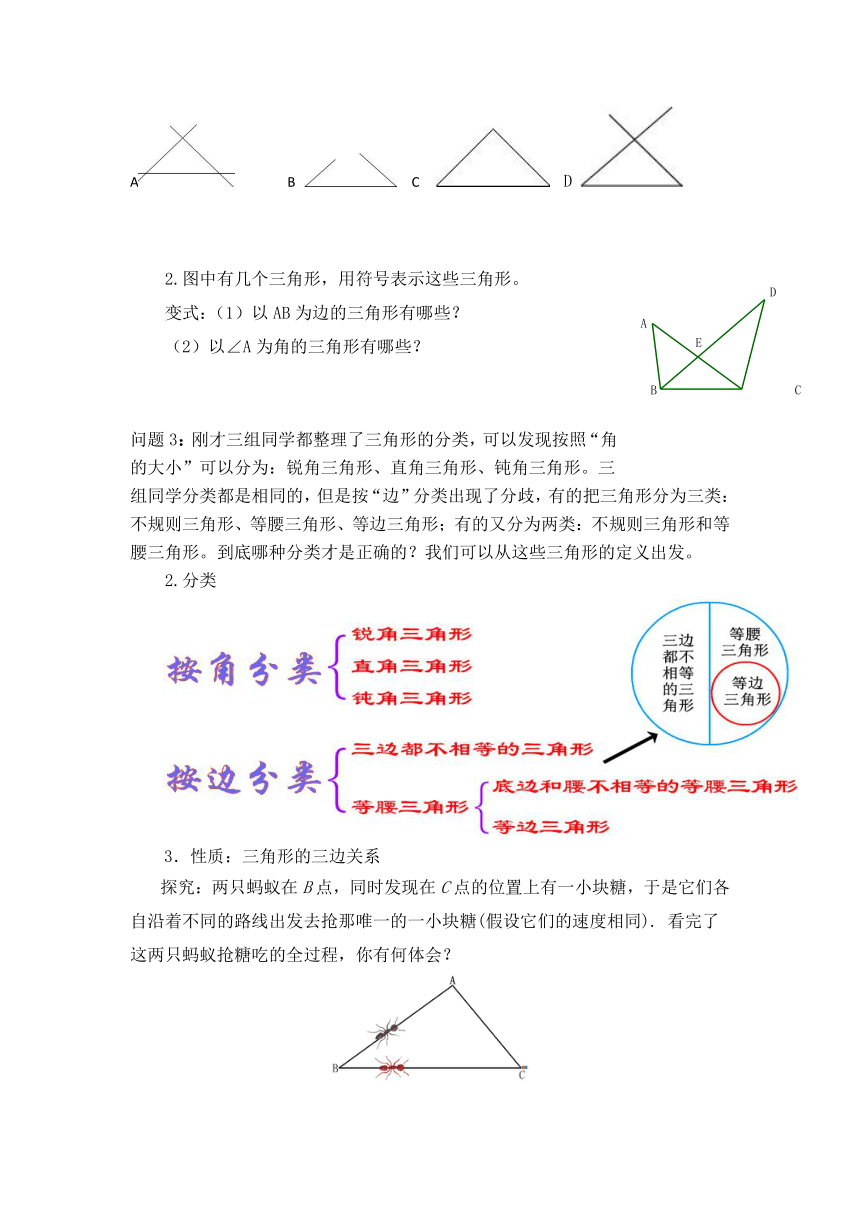
练习:1.观察下列图形,是三角形的是( )
A B C D
(
A
D
C
B
E
)2.图中有几个三角形,用符号表示这些三角形。
变式:(1)以AB为边的三角形有哪些?
(2)以∠A为角的三角形有哪些?
问题3:刚才三组同学都整理了三角形的分类,可以发现按照“角的大小”可以分为:锐角三角形、直角三角形、钝角三角形。三组同学分类都是相同的,但是按“边”分类出现了分歧,有的把三角形分为三类:不规则三角形、等腰三角形、等边三角形;有的又分为两类:不规则三角形和等腰三角形。到底哪种分类才是正确的?我们可以从这些三角形的定义出发。
2.分类
3.性质:三角形的三边关系
探究:两只蚂蚁在B点,同时发现在C点的位置上有一小块糖,于是它们各自沿着不同的路线出发去抢那唯一的一小块糖(假设它们的速度相同). 看完了这两只蚂蚁抢糖吃的全过程,你有何体会?
对于任意一个△ABC,如果把其中任意两个顶点(例如B,C)看成定点,由“两点之间,线段最短”可得 AB+AC>BC ①
同理有 AC+BC>AB ②
AB+BC>AC ③
一般地,我们有
三角形两边的和大于第三边.
由不等式②③移项可得BC>AB-AC,BC>AC-AB. 这就是说,
三角形两边的差小于第三边.
典例解析
例1.判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm、8cm、4cm; (2)5cm、6cm、11cm;(3)5cm、6cm、10cm.
【针对练习】
请在下列横线上填一个数字,使得这三个长度的线段能构成三角形 7 ,4, ______.
例2.用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长是4cm的等腰三角形吗?为什么?
【针对练习】
1.如果等腰三角形的一边长是4cm,另一边长是9cm,则这个等腰三角形的周长为__22___cm.
2.如果等腰三角形的一边长是5cm, 另一边长是8cm, 则这个等腰三角形的周长为_18或21__cm.
例3. △ABC中,AB=3,BC=4,则AC边的长满足( )
A. AC=5 B. AC>1 C. AC<7 D.1【针对练习】
已知三角形的三边长分别为2,a-1,4,则化简|a-3|+|a-7|的结果为A.
A.2a-10 B.10-2a C.4 D.-4
例4.已知a,b,c是△ABC的三边长.
(1)若a,b,c满足,(a-b)2+试判断△ABC的形状;
(2)化简:+-.
【针对练习】
若a、b、c是△ABC的三边,化简:|a﹣b+c|﹣2|c﹣a﹣b|+3|a+b+c|的值.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
达标检测
1.下图中一共有_____个三角形,它们分别是__________________________.
2.下列各图中各有几个三角形
3.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个图中,能正确表示它们之间关系的是( )
A. B. C. D.
4.已知三角形的两边长分别是4cm和9cm,如果第三边长是奇数,求第三边的长_______________________________.
5.定义:若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有( )
A.1对 B.2对 C.3对 D.4对
6.如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数是( )
A.2 B.3 C.4 D.5
7.判断下列所给的三条线段是否能围成三角形
(1)5cm,5cm,a cm(0<a<10);(2)a+1,a+2,a+3;(3)三条线段之比为2:3:5.
8.若a、b、c是△ABC的三边,化简:|a﹣b+c|﹣2|c﹣a﹣b|+3|a+b+c|的值.
9.已知的三边长分别为a,b,c.
(1)若a,b,c满足(a-b)2+(b-c)2=0,试判断△ABC的形状:
(2)若a=5,b=2,且c为整数,求△ABC的周长的最大值及最小值.
作业布置:
(1)必做题:作业本
(2)选做题:如图,若△ABC的三边长为a,b,c,
试化简:|a-b-c|+|b-c-a|+|c-a-b|
五、教学反思:
本节课让学生经历一个探究解决问题的过程,抓住“任意的三条线段能不能围成一个三角形”引发学生探究的欲望,围绕这个问题让学生自己动手操作,发现有的能围成,有的不能围成,由学生自己找出原因,为什么能?为什么不能?初步感知三条边之间的关系,重点研究“能围成三角形的三条边之间到底有什么关系”.通过观察、验证、再操作,最终发现三角形任意两边之和大于第三边这一结论.这样教学符合学生的认知特点,既提高了学生学习的兴趣,又增强了学生的动手能力
素养目标:
1.结合具体的实例,进一步认识三角形的概念及其基本要素.
2.会用符号、字母表示三角形,并能按边的相等关系对三角形进行分类.
3.理解三角形两边之和大于第三边与两边之差小于第三边的性质,并会初步运用这些性质解决问题.
4.会用数学的语言描述三角形的三边关系.
一.教学目标:
1.知识与技能:(1)认识三角形并会用几何语言表示三角形,了解三角形分类.
(2)掌握三角形的三边关系. (3)运用三角形三边关系解决有关的问题
2.过程与方法:通过回顾小学已学过的知识,以学生为中心进一步学习三角形的相关知识,体现学生的主体地位;
3.情感与态度:在利用所学知识进行解题的过程中,培养学生学习数学的兴趣和探究的能力。
二.教学重、难点:
重点:认识三角形的边,内角,顶点,能用符号语言表示三角形。
难点:运用三角形三边的不等关系解决生活实际问题。
教学方法:指导---自主学习
教学准备:课件,三角尺
教学过程设计
1.温故知新
问题1:我们一起来回顾:一条线可以成为哪些几何图形?
问题2:增加一条线,两条线可以组成哪些已学过的几何图形
问题3:老师再增加一条线,三条线又可以组成哪些几何图形
2.情境引入
出示著名建筑、金字塔、战机、大桥等图片,让学生感受生活中的三角形,体会生活中处处有数学.教师利用多媒体演示三角形的形成过程,让学生观察.
思考:(1)从古埃及的金字塔到现代的飞机,从宏伟的建筑物到微小的分子结构,都有什么样的形象?(2)在我们的生活中有没有这样的形象呢?试举例.
3.新知学习
问题1:在小学我们已经初步学习了三角形的有关知识,请同学们根据小学所学的知识,说一说你对三角形有哪些认识?学生小组交流并展示汇报。
问题2:从各组汇报展示结果来看,大家主要从哪些方面来研究三角形?
师归纳:从定义、分类、性质三方面研究三角形,也是我们研究几何图形的一般思路。
1.定义:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
线段AB,BC,CA是三角形的边. 点A,B,C是三角形的顶点. ∠A,∠B,∠C是相邻两边组成的角,叫做三角形的内角,简称三角形的角.
顶点是A,B,C的三角形,记作△ABC,读作“三角形ABC”.
△ABC的三边,有时也用a,b,c来表示. 顶点A所对的边BC用a表示,顶点B所对的边AC用b表示,顶点C所对的边AB用c表示.
练习:1.观察下列图形,是三角形的是( )
A B C D
(
A
D
C
B
E
)2.图中有几个三角形,用符号表示这些三角形。
变式:(1)以AB为边的三角形有哪些?
(2)以∠A为角的三角形有哪些?
问题3:刚才三组同学都整理了三角形的分类,可以发现按照“角的大小”可以分为:锐角三角形、直角三角形、钝角三角形。三组同学分类都是相同的,但是按“边”分类出现了分歧,有的把三角形分为三类:不规则三角形、等腰三角形、等边三角形;有的又分为两类:不规则三角形和等腰三角形。到底哪种分类才是正确的?我们可以从这些三角形的定义出发。
2.分类
3.性质:三角形的三边关系
探究:两只蚂蚁在B点,同时发现在C点的位置上有一小块糖,于是它们各自沿着不同的路线出发去抢那唯一的一小块糖(假设它们的速度相同). 看完了这两只蚂蚁抢糖吃的全过程,你有何体会?
对于任意一个△ABC,如果把其中任意两个顶点(例如B,C)看成定点,由“两点之间,线段最短”可得 AB+AC>BC ①
同理有 AC+BC>AB ②
AB+BC>AC ③
一般地,我们有
三角形两边的和大于第三边.
由不等式②③移项可得BC>AB-AC,BC>AC-AB. 这就是说,
三角形两边的差小于第三边.
典例解析
例1.判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm、8cm、4cm; (2)5cm、6cm、11cm;(3)5cm、6cm、10cm.
【针对练习】
请在下列横线上填一个数字,使得这三个长度的线段能构成三角形 7 ,4, ______.
例2.用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长是4cm的等腰三角形吗?为什么?
【针对练习】
1.如果等腰三角形的一边长是4cm,另一边长是9cm,则这个等腰三角形的周长为__22___cm.
2.如果等腰三角形的一边长是5cm, 另一边长是8cm, 则这个等腰三角形的周长为_18或21__cm.
例3. △ABC中,AB=3,BC=4,则AC边的长满足( )
A. AC=5 B. AC>1 C. AC<7 D.1
已知三角形的三边长分别为2,a-1,4,则化简|a-3|+|a-7|的结果为A.
A.2a-10 B.10-2a C.4 D.-4
例4.已知a,b,c是△ABC的三边长.
(1)若a,b,c满足,(a-b)2+试判断△ABC的形状;
(2)化简:+-.
【针对练习】
若a、b、c是△ABC的三边,化简:|a﹣b+c|﹣2|c﹣a﹣b|+3|a+b+c|的值.
课堂小结
1.本节课你有哪些收获?2.还有没解决的问题吗?
达标检测
1.下图中一共有_____个三角形,它们分别是__________________________.
2.下列各图中各有几个三角形
3.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个图中,能正确表示它们之间关系的是( )
A. B. C. D.
4.已知三角形的两边长分别是4cm和9cm,如果第三边长是奇数,求第三边的长_______________________________.
5.定义:若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有( )
A.1对 B.2对 C.3对 D.4对
6.如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数是( )
A.2 B.3 C.4 D.5
7.判断下列所给的三条线段是否能围成三角形
(1)5cm,5cm,a cm(0<a<10);(2)a+1,a+2,a+3;(3)三条线段之比为2:3:5.
8.若a、b、c是△ABC的三边,化简:|a﹣b+c|﹣2|c﹣a﹣b|+3|a+b+c|的值.
9.已知的三边长分别为a,b,c.
(1)若a,b,c满足(a-b)2+(b-c)2=0,试判断△ABC的形状:
(2)若a=5,b=2,且c为整数,求△ABC的周长的最大值及最小值.
作业布置:
(1)必做题:作业本
(2)选做题:如图,若△ABC的三边长为a,b,c,
试化简:|a-b-c|+|b-c-a|+|c-a-b|
五、教学反思:
本节课让学生经历一个探究解决问题的过程,抓住“任意的三条线段能不能围成一个三角形”引发学生探究的欲望,围绕这个问题让学生自己动手操作,发现有的能围成,有的不能围成,由学生自己找出原因,为什么能?为什么不能?初步感知三条边之间的关系,重点研究“能围成三角形的三条边之间到底有什么关系”.通过观察、验证、再操作,最终发现三角形任意两边之和大于第三边这一结论.这样教学符合学生的认知特点,既提高了学生学习的兴趣,又增强了学生的动手能力
