4.5牛顿运动定律的应用 导学案 高一上学期物理人教版(2019)必修第一册
文档属性
| 名称 | 4.5牛顿运动定律的应用 导学案 高一上学期物理人教版(2019)必修第一册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-10 00:00:00 | ||
图片预览


文档简介
4.5牛顿运动定律的应用
一、学习目标
1、进一步学习物体的受力情况,并能结合物体的运动情况进行受力分析。(重点)
2、知道动力学的两类问题:从受力确定运动情况和从运动情况确定受力.理解加速度是解决两类动力学问题的桥梁。(重点) 3、掌握解决动力学问题的基本思路和方法,会用牛顿运动定律和运动学公式解决有关问题。(难点)
二、复习回顾
1、运动学公式
2、牛顿运动定律
第一定律:一切物体总保持匀速直线运动状态或静止状态,除非作用在它上面的力迫使它改变这种状态。
第二定律:物体加速度的大小跟所受到的作用力成正比,跟它的质量成反比; 加速度方向跟作用力方向相同。公式: F=ma
第三定律:两个物体之间的作用力和反作用力总是大小相等,方向相反,作用在一条直线上。
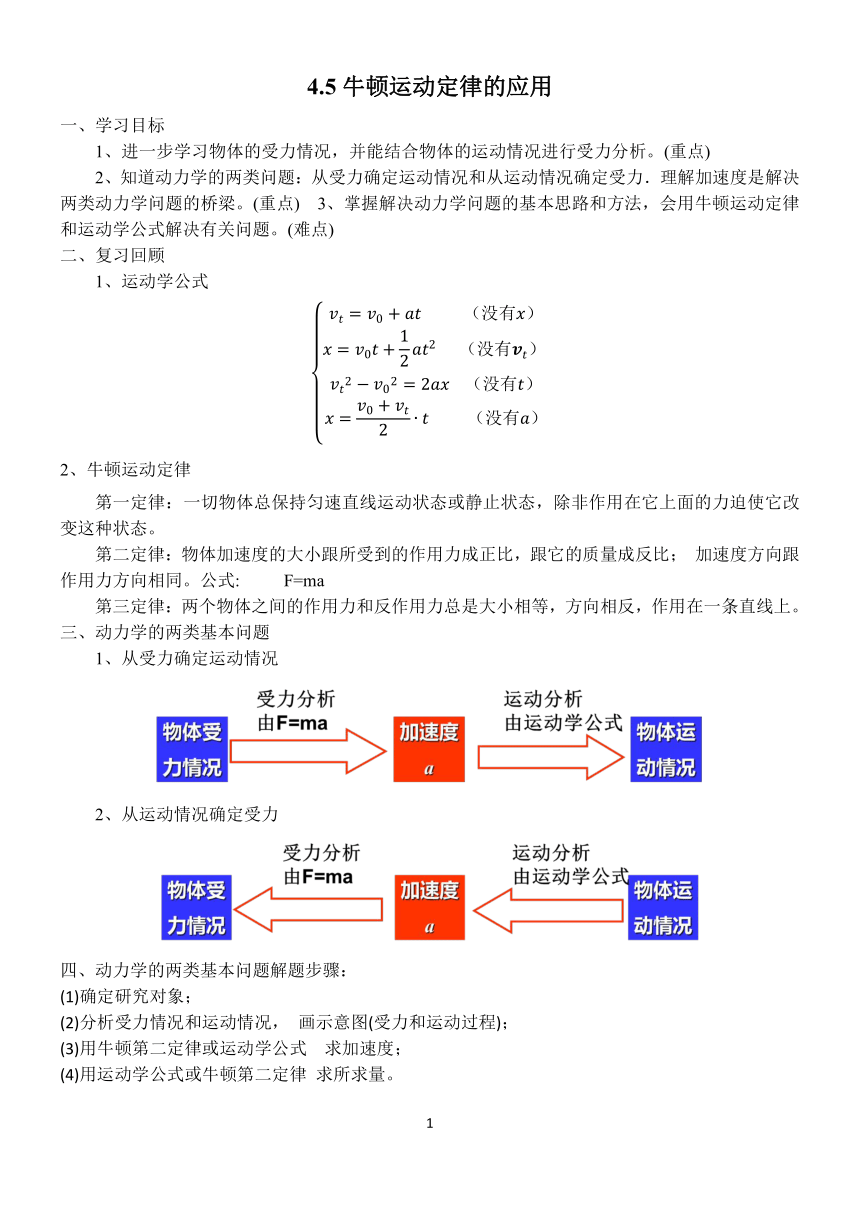
三、动力学的两类基本问题
1、从受力确定运动情况
2、从运动情况确定受力
四、动力学的两类基本问题解题步骤:
(1)确定研究对象;
(2)分析受力情况和运动情况, 画示意图(受力和运动过程);
(3)用牛顿第二定律或运动学公式 求加速度;
(4)用运动学公式或牛顿第二定律 求所求量。
例题1.运动员把冰壶沿水平冰面投出,让冰壶在冰面上自由滑行,在不与其他冰壶碰撞的情况下,最终停在远处的某个位置。按比赛规则,投掷冰壶运动员的队友,可以用毛刷在冰壶滑行前方来回摩擦冰面,减小冰面的动摩擦因数以调节冰壶的运动。
(1)运动员以 3.4 m/s 的速度投掷冰壶,若冰壶和冰面的动摩擦因数为 0.02,冰壶能在冰面上滑行多远?g 取 10 m/s2。
(2)若运动员仍以 3.4 m/s 的速度将冰壶投出,其队友在冰壶自由滑行 10 m 后开始在其滑行前方摩擦冰面,冰壶和冰面的动摩擦因数变为原来的 90%,冰壶多滑行了多少距离?
例题2.一位滑雪者,人与装备的总质量为75kg,以2m/s的初速度沿山坡匀加速直线滑下,山坡的倾角为30°,在5s的时间内滑下的路程为60m,求滑雪者对雪面的压力及滑雪者受到的阻力(包括摩擦和空气阻力),g取10m/s2。
巩固练习
1.质量为1 kg的质点,受水平恒力作用,由静止开始做匀加速直线运动,它在t s内的位移为x m,则F的大小为(单位为N)( ).
A. B. C. D.
2.如图所示,水平恒力F=20 N,把质量m=0.6 kg的木块压在竖直墙上,木块离地面的高度H=6 m.木块从静止开始向下做匀加速运动,经过2 s到达地面.
(取g=10 m/s2) 求:
(1)木块下滑的加速度a的大小;
(2)木块与墙壁之间的动摩擦因数.
3.如图所示,楼梯口一倾斜的天花板与水平面成θ=37°,一装潢工人手持木杆绑着刷子粉刷天花板,工人所持木杆对刷子的作用力始终保持竖直向上,大小为F=10 N,刷子的质量为m=0.5 kg,刷子可视为质点,刷子与天花板间的动摩擦因数为0.5,天花板长为L=4 m,取sin 37°=0.6,试求:(1)刷子沿天花板向上运动的加速度大小;
(2)工人把刷子从天花板底端推到顶端所用的时间.
4.如图所示,在倾角θ=37°的足够长的固定的斜面底端有一质量m=1.0kg的物体.物体与斜面间动摩擦因数 =0.25,现用轻细绳将物体由静止沿斜面向上拉动.拉力F=10N,方向平行斜面向上.经时间t=4s绳子突然断了,求:
(1)绳断时物体的速度大小.
(2)从绳子断了开始到物体再返回到斜面底端的运动时间.(sin37°=0.60, cos37°=0.80,g=10m/s2)
5.如图所示,木块质量m=0.78kg,在与水平方向成37°角、斜向右上方的恒定拉力F作用下,从静止开始做匀加速直线运动,在3s时间内运动了9m的位移.已知木块与地面间的动摩擦因数μ=0.4,取重力加速度g=10m/s2,sin37°=0.60,cos37°=0.80.
(1)求拉力F的大小
(2)若在3s末时撤去拉力F,求物体还能运动多长时间
以及物体还能滑行的最大位移.
6.如图所示,质量m=2 kg的物体静止于水平地面的A处,A、B间距L=20 m,用大小为30 N,沿水平方向的外力拉此物体,经t0=2 s拉至B处。(已知cos37°=0.8,sin37°=0.6,取g=10 m/s2)
(1)求物体与地面间的动摩擦因数μ;
(2)用大小为30 N,与水平方向成37°的力斜向上拉此物体,使物体从A处由静止开始运动并能到达B处,求该力作用的最短时间t。
7.如图所示,质量M=0.1 kg的有孔小球穿在固定的足够长的斜杆上,斜杆与水平方向的夹角θ=37°,球与杆间的动摩擦因数μ=0.5.小球受到竖直向上的恒定拉力F=1.2 N后,由静止开始沿杆斜向上做匀加速直线运动.求(sin37°=0.6,cos37°=0.8,重力加速度g取10 m/s2):
(1)斜杆对小球的滑动摩擦力的大小;
(2)小球的加速度;
(3)最初2 s内小球的位移.
一、学习目标
1、进一步学习物体的受力情况,并能结合物体的运动情况进行受力分析。(重点)
2、知道动力学的两类问题:从受力确定运动情况和从运动情况确定受力.理解加速度是解决两类动力学问题的桥梁。(重点) 3、掌握解决动力学问题的基本思路和方法,会用牛顿运动定律和运动学公式解决有关问题。(难点)
二、复习回顾
1、运动学公式
2、牛顿运动定律
第一定律:一切物体总保持匀速直线运动状态或静止状态,除非作用在它上面的力迫使它改变这种状态。
第二定律:物体加速度的大小跟所受到的作用力成正比,跟它的质量成反比; 加速度方向跟作用力方向相同。公式: F=ma
第三定律:两个物体之间的作用力和反作用力总是大小相等,方向相反,作用在一条直线上。
三、动力学的两类基本问题
1、从受力确定运动情况
2、从运动情况确定受力
四、动力学的两类基本问题解题步骤:
(1)确定研究对象;
(2)分析受力情况和运动情况, 画示意图(受力和运动过程);
(3)用牛顿第二定律或运动学公式 求加速度;
(4)用运动学公式或牛顿第二定律 求所求量。
例题1.运动员把冰壶沿水平冰面投出,让冰壶在冰面上自由滑行,在不与其他冰壶碰撞的情况下,最终停在远处的某个位置。按比赛规则,投掷冰壶运动员的队友,可以用毛刷在冰壶滑行前方来回摩擦冰面,减小冰面的动摩擦因数以调节冰壶的运动。
(1)运动员以 3.4 m/s 的速度投掷冰壶,若冰壶和冰面的动摩擦因数为 0.02,冰壶能在冰面上滑行多远?g 取 10 m/s2。
(2)若运动员仍以 3.4 m/s 的速度将冰壶投出,其队友在冰壶自由滑行 10 m 后开始在其滑行前方摩擦冰面,冰壶和冰面的动摩擦因数变为原来的 90%,冰壶多滑行了多少距离?
例题2.一位滑雪者,人与装备的总质量为75kg,以2m/s的初速度沿山坡匀加速直线滑下,山坡的倾角为30°,在5s的时间内滑下的路程为60m,求滑雪者对雪面的压力及滑雪者受到的阻力(包括摩擦和空气阻力),g取10m/s2。
巩固练习
1.质量为1 kg的质点,受水平恒力作用,由静止开始做匀加速直线运动,它在t s内的位移为x m,则F的大小为(单位为N)( ).
A. B. C. D.
2.如图所示,水平恒力F=20 N,把质量m=0.6 kg的木块压在竖直墙上,木块离地面的高度H=6 m.木块从静止开始向下做匀加速运动,经过2 s到达地面.
(取g=10 m/s2) 求:
(1)木块下滑的加速度a的大小;
(2)木块与墙壁之间的动摩擦因数.
3.如图所示,楼梯口一倾斜的天花板与水平面成θ=37°,一装潢工人手持木杆绑着刷子粉刷天花板,工人所持木杆对刷子的作用力始终保持竖直向上,大小为F=10 N,刷子的质量为m=0.5 kg,刷子可视为质点,刷子与天花板间的动摩擦因数为0.5,天花板长为L=4 m,取sin 37°=0.6,试求:(1)刷子沿天花板向上运动的加速度大小;
(2)工人把刷子从天花板底端推到顶端所用的时间.
4.如图所示,在倾角θ=37°的足够长的固定的斜面底端有一质量m=1.0kg的物体.物体与斜面间动摩擦因数 =0.25,现用轻细绳将物体由静止沿斜面向上拉动.拉力F=10N,方向平行斜面向上.经时间t=4s绳子突然断了,求:
(1)绳断时物体的速度大小.
(2)从绳子断了开始到物体再返回到斜面底端的运动时间.(sin37°=0.60, cos37°=0.80,g=10m/s2)
5.如图所示,木块质量m=0.78kg,在与水平方向成37°角、斜向右上方的恒定拉力F作用下,从静止开始做匀加速直线运动,在3s时间内运动了9m的位移.已知木块与地面间的动摩擦因数μ=0.4,取重力加速度g=10m/s2,sin37°=0.60,cos37°=0.80.
(1)求拉力F的大小
(2)若在3s末时撤去拉力F,求物体还能运动多长时间
以及物体还能滑行的最大位移.
6.如图所示,质量m=2 kg的物体静止于水平地面的A处,A、B间距L=20 m,用大小为30 N,沿水平方向的外力拉此物体,经t0=2 s拉至B处。(已知cos37°=0.8,sin37°=0.6,取g=10 m/s2)
(1)求物体与地面间的动摩擦因数μ;
(2)用大小为30 N,与水平方向成37°的力斜向上拉此物体,使物体从A处由静止开始运动并能到达B处,求该力作用的最短时间t。
7.如图所示,质量M=0.1 kg的有孔小球穿在固定的足够长的斜杆上,斜杆与水平方向的夹角θ=37°,球与杆间的动摩擦因数μ=0.5.小球受到竖直向上的恒定拉力F=1.2 N后,由静止开始沿杆斜向上做匀加速直线运动.求(sin37°=0.6,cos37°=0.8,重力加速度g取10 m/s2):
(1)斜杆对小球的滑动摩擦力的大小;
(2)小球的加速度;
(3)最初2 s内小球的位移.
