3.1勾股定理(2)学案(无答案)2023-2024学年苏科版八年级数学 上册
文档属性
| 名称 | 3.1勾股定理(2)学案(无答案)2023-2024学年苏科版八年级数学 上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 87.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 00:00:00 | ||
图片预览

文档简介
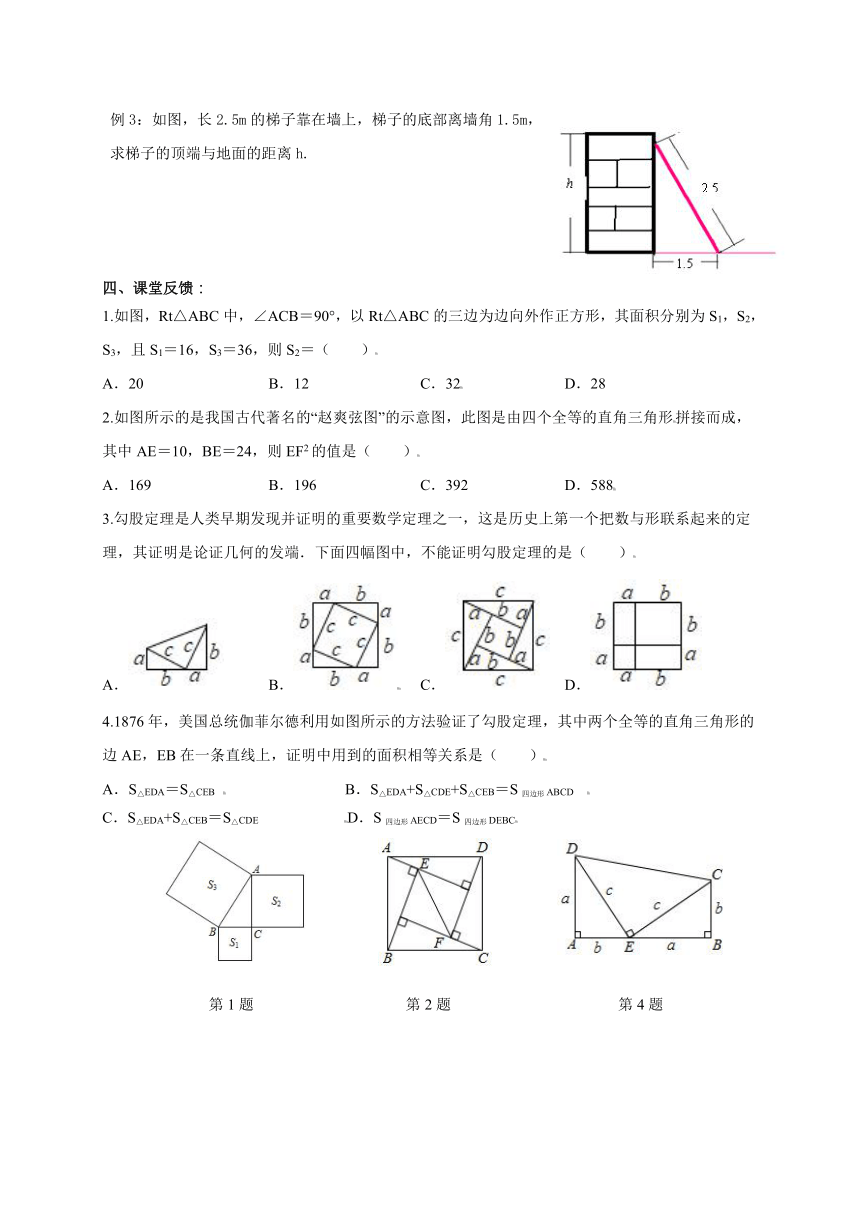
2023年秋学期八年级数学学案
课题: 3.1勾股定理(2) 班级: 姓名: 学号:
〖自学自测展素养〗
学习目标:
1、通过拼图,用面积的方法说明勾股定理的正确性.
2、通过实例应用勾股定理,培养学生的知识应用技能.
〖研学随练展收获〗
一、复习回顾:
勾股定理:
如图:如果直角三角形两直角边分别为a,b,斜边为c,则有: 。
二、活动探究:
活动一:
1、准备4张全等的直角三角形纸片。
2、把这4张纸片拼成一个以c为边长的正方形吗?
3、你能利用该图形验证勾股定理吗?
活动二:如图,把火柴盒放倒,在这个过程中,也能验证勾股定理,你会利用这个图验证勾股定理吗?把你的想法与大家交流一下.
三、例题分析:
例1:在Rt△ABC中,∠C=90°.
(1) 已知:BC=9,AC=12,则AB =______; (2) 已知:BC=8,AB=10,则AC=______;
(3) 已知:a=40,c=41,则b =______; (4) 已知:c=39,b=15,a =______;
(5) 已知: a:b=3:4, c=15,则a=______,b=______.
例2:如图,是由四个全等的直角三角形与中间一个小正方形拼成的个大正方形,若大正方形的面积是17,小正方形的面积是1,直角三角形的两直角边分别为a,b,则(a+b)2的值是______
例3:如图,长2.5m的梯子靠在墙上,梯子的底部离墙角1.5m,求梯子的顶端与地面的距离h.
四、课堂反馈:
1.如图,Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=16,S3=36,则S2=( )
A.20 B.12 C.32 D.28
2.如图所示的是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=10,BE=24,则EF2的值是( )
A.169 B.196 C.392 D.588
3.勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
4.1876年,美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边AE,EB在一条直线上,证明中用到的面积相等关系是( )
A.S△EDA=S△CEB B.S△EDA+S△CDE+S△CEB=S四边形ABCD
C.S△EDA+S△CEB=S△CDE D.S四边形AECD=S四边形DEBC
第1题 第2题 第4题
【校本作业】
一、必做题
1.一个直角三角形,两直角边长分别为3和4,下列说法正确的是 ( )
A.斜边长为25 B.三角形的周长为25 C.斜边长为5 D.三角形面积为20
2.如图,如果将△ABC的顶点A先向下平移3格,再向左平移1格到达A'点,连接A'B,则线段A'B与线段AC的关系是 ( )
A.垂直 B.相等 C.平分 D.平分且垂直
3.如图,已知1号,4号两个正方形的面积和为7,2号,3号两个正方形的而积和为4,则a,b,c三个方形的面积和为 ( )
A.10 B.13
C.15 D.22
如图,在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为 ( )
A.2 B.2.6 C.3 D.4
5.如图,在长方形纸片ABCD中,AB=12,BC= 5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A'处,则AE的长为 .
6.如图,在一个长方形木板上截下△ABC,使AC=6 cm,BC=8 cm,则截线AB= ;点C到AB的距离= .
7.若AC=6,BC=5,将图①中的四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图②所示的“数学风车”,则这个风车的外围周长是 .
第5题 第6题 第7题
8.如图,在四边形.ABCD中,∠BAD=90°,∠DBC=90°,AD=3,AB=4,BC=12.求CD的长.
9.如图,直角三角形纸片的两直角边的长分别为AC=6 cm,BC=8 cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合.求CD的长.
二、选做题
10. 如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE丄DF,交AB于E,交BC于F,若AE=4,FC=3,求EF长.
三、拓展题
11.学习勾股定理时,我们学会运用图1验证它的正确性.图中大正方形的面积可表示为(a+b)2,也可表示为c2+4×ab,即(a+b)2=c2+4×ab.由此推出勾股定理a2+b2=c2这种方法可以极简单地直观推论或验证出数学规律和公式.
(1)请你用图(Ⅱ)的面积表达式验证勾股定理(其中四个全等的直角三角形围成一个大正方形ABCD,中间的部分是一个小正方形EFGH,AE=a,BE=b,AB=c);
(2)请你用图(Ⅲ)提供的图形进行组合,用组合图形的面积表达式验证:(x+y)2=x2+2xy +y2.
课题: 3.1勾股定理(2) 班级: 姓名: 学号:
〖自学自测展素养〗
学习目标:
1、通过拼图,用面积的方法说明勾股定理的正确性.
2、通过实例应用勾股定理,培养学生的知识应用技能.
〖研学随练展收获〗
一、复习回顾:
勾股定理:
如图:如果直角三角形两直角边分别为a,b,斜边为c,则有: 。
二、活动探究:
活动一:
1、准备4张全等的直角三角形纸片。
2、把这4张纸片拼成一个以c为边长的正方形吗?
3、你能利用该图形验证勾股定理吗?
活动二:如图,把火柴盒放倒,在这个过程中,也能验证勾股定理,你会利用这个图验证勾股定理吗?把你的想法与大家交流一下.
三、例题分析:
例1:在Rt△ABC中,∠C=90°.
(1) 已知:BC=9,AC=12,则AB =______; (2) 已知:BC=8,AB=10,则AC=______;
(3) 已知:a=40,c=41,则b =______; (4) 已知:c=39,b=15,a =______;
(5) 已知: a:b=3:4, c=15,则a=______,b=______.
例2:如图,是由四个全等的直角三角形与中间一个小正方形拼成的个大正方形,若大正方形的面积是17,小正方形的面积是1,直角三角形的两直角边分别为a,b,则(a+b)2的值是______
例3:如图,长2.5m的梯子靠在墙上,梯子的底部离墙角1.5m,求梯子的顶端与地面的距离h.
四、课堂反馈:
1.如图,Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=16,S3=36,则S2=( )
A.20 B.12 C.32 D.28
2.如图所示的是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=10,BE=24,则EF2的值是( )
A.169 B.196 C.392 D.588
3.勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
4.1876年,美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边AE,EB在一条直线上,证明中用到的面积相等关系是( )
A.S△EDA=S△CEB B.S△EDA+S△CDE+S△CEB=S四边形ABCD
C.S△EDA+S△CEB=S△CDE D.S四边形AECD=S四边形DEBC
第1题 第2题 第4题
【校本作业】
一、必做题
1.一个直角三角形,两直角边长分别为3和4,下列说法正确的是 ( )
A.斜边长为25 B.三角形的周长为25 C.斜边长为5 D.三角形面积为20
2.如图,如果将△ABC的顶点A先向下平移3格,再向左平移1格到达A'点,连接A'B,则线段A'B与线段AC的关系是 ( )
A.垂直 B.相等 C.平分 D.平分且垂直
3.如图,已知1号,4号两个正方形的面积和为7,2号,3号两个正方形的而积和为4,则a,b,c三个方形的面积和为 ( )
A.10 B.13
C.15 D.22
如图,在△ABC中,∠ACB=90°,AC=12,BC=5,AM=AC,BN=BC,则MN的长为 ( )
A.2 B.2.6 C.3 D.4
5.如图,在长方形纸片ABCD中,AB=12,BC= 5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A'处,则AE的长为 .
6.如图,在一个长方形木板上截下△ABC,使AC=6 cm,BC=8 cm,则截线AB= ;点C到AB的距离= .
7.若AC=6,BC=5,将图①中的四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图②所示的“数学风车”,则这个风车的外围周长是 .
第5题 第6题 第7题
8.如图,在四边形.ABCD中,∠BAD=90°,∠DBC=90°,AD=3,AB=4,BC=12.求CD的长.
9.如图,直角三角形纸片的两直角边的长分别为AC=6 cm,BC=8 cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合.求CD的长.
二、选做题
10. 如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE丄DF,交AB于E,交BC于F,若AE=4,FC=3,求EF长.
三、拓展题
11.学习勾股定理时,我们学会运用图1验证它的正确性.图中大正方形的面积可表示为(a+b)2,也可表示为c2+4×ab,即(a+b)2=c2+4×ab.由此推出勾股定理a2+b2=c2这种方法可以极简单地直观推论或验证出数学规律和公式.
(1)请你用图(Ⅱ)的面积表达式验证勾股定理(其中四个全等的直角三角形围成一个大正方形ABCD,中间的部分是一个小正方形EFGH,AE=a,BE=b,AB=c);
(2)请你用图(Ⅲ)提供的图形进行组合,用组合图形的面积表达式验证:(x+y)2=x2+2xy +y2.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
