3.1勾股定理(1)学案(无答案)2023-2024学年苏科版八年级数学上册
文档属性
| 名称 | 3.1勾股定理(1)学案(无答案)2023-2024学年苏科版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 203.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 00:00:00 | ||
图片预览

文档简介
2023年秋学期八年级数学学案
课题:3.1勾股定理(1) 班级: 姓名: 学号:
〖自学自测展素养〗
1.知道直角三角形的三边之间的数量关系.
2.会用割补法计算图形面积.
3.经历“观察—猜想—归纳—验证”的数学思想,并体会数形结合和从特殊到一般的思想方法.
〖研学随练展收获〗
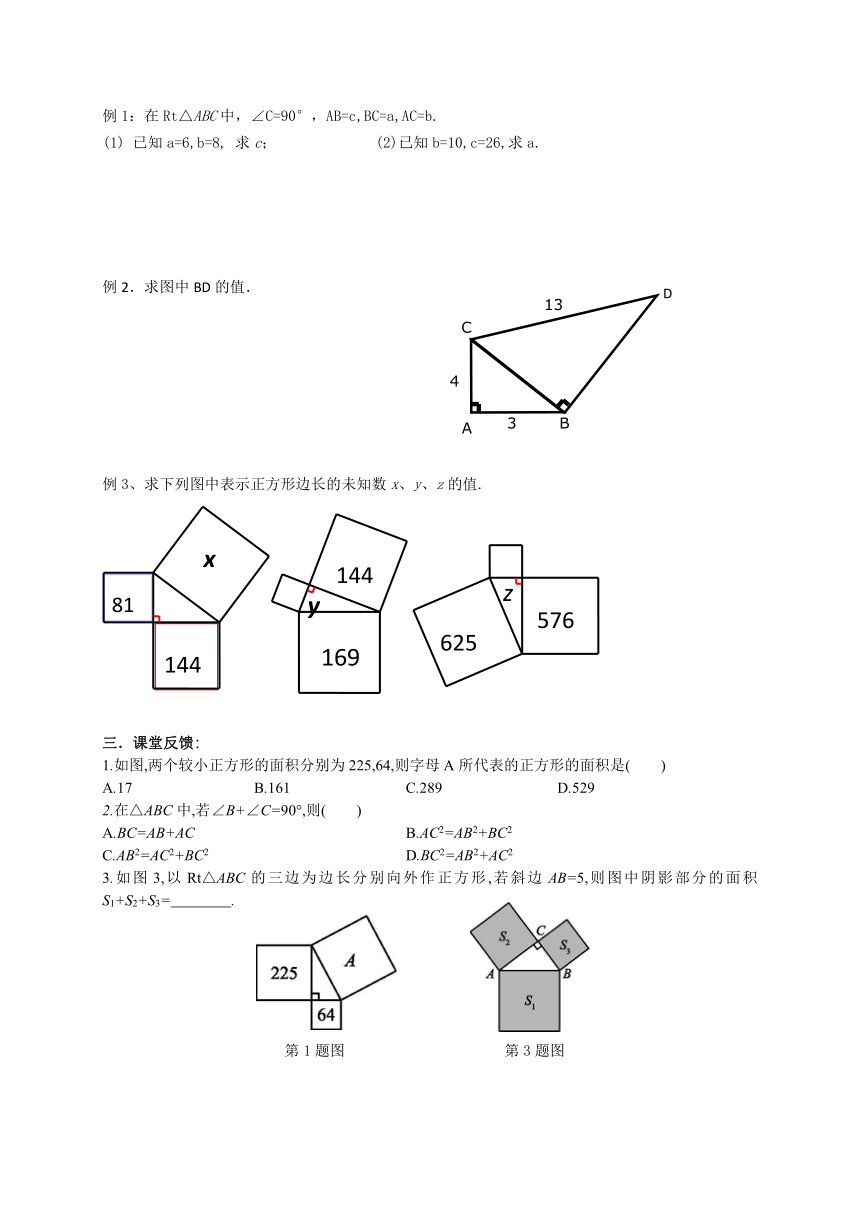
自学课本78至79页,并完成以下问题:
(1)如何求正方形R的面积?与同伴交流你的做法.
(2)分析3个正方形面积,你有什么发现?
(3)直角三角形三边有怎样的数量关系?
【活动探究】
是否所有的直角三角形都有这个性质呢?请动手验证。
【小组成员在方格纸上任意作出一个直角三角形,,注意:三角形各顶点都必须在格点上,再分别以AB、AC、BC为边向外作正方形,计算,探究3个正方形面积之间的数量关系
勾股定理:
如图所示:在直角三角形中,三边分别为a、b、c,则
例1:在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.
已知a=6,b=8, 求c; (2)已知b=10,c=26,求a.
(
A
4
B
C
3
13
D
)
例2.求图中BD的值.
例3、求下列图中表示正方形边长的未知数x、y、z的值.
(
x
y
z
576
625
144
169
144
81
)
三.课堂反馈:
1.如图,两个较小正方形的面积分别为225,64,则字母A所代表的正方形的面积是( )
A.17 B.161 C.289 D.529
2.在△ABC中,若∠B+∠C=90°,则( )
A.BC=AB+AC B.AC2=AB2+BC2
C.AB2=AC2+BC2 D.BC2=AB2+AC2
3.如图3,以Rt△ABC的三边为边长分别向外作正方形,若斜边AB=5,则图中阴影部分的面积S1+S2+S3= .
第1题图 第3题图
【校本作业】
一、必做题
判断题
(1)若a、b、c是三角形的三边,则。 ( )
(2)直角三角形中,两边的平方和等于第三边的平方。 ( )
(3)直角三角形中,∠A=90°,则 。 ( )
2、求下列直角三角形中未知边的长.
3、如图,△ABC的顶点A,B,C均在边长为1的小正方形组成的网格的格点上,BD⊥AC于点D,则BD的长为( )
A.0.8 B.1.6
C.3.2 D.4.8
4.一直角三角形的三边分别为2、3、x,那么以x为边长的正方形的面积为( )
A.13 B.5 C.13或5 D.4
5.下列各数组中,不能作为直角三角形三边长的是 ( )
A. 9,12,15 B. 7,24,25 C. 6,8,10 D. 3,5,7
6、在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.
(1)若a=7,b=24,求c (2)若c=15,b=12,求a (3)若a∶b=3∶4,c=10,求a,b
7、如图8,某人划船横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B 5 m,结果他在水中实际划了13 m,求该河流的宽度.
8、如图12,在△ABC中,AC⊥BC,AE平分∠BAC交BC于点E,DE⊥AB于点D,BC=12 cm,AC=5 cm,求BE的长.
9.如图,在△ABC中,∠ACB=90°,BC=6,AC=8,CD是高.
(1)求AB的长;
(2)求△ABC的面积;
(3)求CD的长.
二、选做题
10.一等腰三角形底边长为10cm,腰长为13cm,则腰上的高为 ( )
A. 12cm B. C. D.
11.如图所示,,,,求正方形的面积.
三、拓展题
12. 如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE丄DF,交AB于E,交BC于F,若AE=4,FC=3,求EF长.
课题:3.1勾股定理(1) 班级: 姓名: 学号:
〖自学自测展素养〗
1.知道直角三角形的三边之间的数量关系.
2.会用割补法计算图形面积.
3.经历“观察—猜想—归纳—验证”的数学思想,并体会数形结合和从特殊到一般的思想方法.
〖研学随练展收获〗
自学课本78至79页,并完成以下问题:
(1)如何求正方形R的面积?与同伴交流你的做法.
(2)分析3个正方形面积,你有什么发现?
(3)直角三角形三边有怎样的数量关系?
【活动探究】
是否所有的直角三角形都有这个性质呢?请动手验证。
【小组成员在方格纸上任意作出一个直角三角形,,注意:三角形各顶点都必须在格点上,再分别以AB、AC、BC为边向外作正方形,计算,探究3个正方形面积之间的数量关系
勾股定理:
如图所示:在直角三角形中,三边分别为a、b、c,则
例1:在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.
已知a=6,b=8, 求c; (2)已知b=10,c=26,求a.
(
A
4
B
C
3
13
D
)
例2.求图中BD的值.
例3、求下列图中表示正方形边长的未知数x、y、z的值.
(
x
y
z
576
625
144
169
144
81
)
三.课堂反馈:
1.如图,两个较小正方形的面积分别为225,64,则字母A所代表的正方形的面积是( )
A.17 B.161 C.289 D.529
2.在△ABC中,若∠B+∠C=90°,则( )
A.BC=AB+AC B.AC2=AB2+BC2
C.AB2=AC2+BC2 D.BC2=AB2+AC2
3.如图3,以Rt△ABC的三边为边长分别向外作正方形,若斜边AB=5,则图中阴影部分的面积S1+S2+S3= .
第1题图 第3题图
【校本作业】
一、必做题
判断题
(1)若a、b、c是三角形的三边,则。 ( )
(2)直角三角形中,两边的平方和等于第三边的平方。 ( )
(3)直角三角形中,∠A=90°,则 。 ( )
2、求下列直角三角形中未知边的长.
3、如图,△ABC的顶点A,B,C均在边长为1的小正方形组成的网格的格点上,BD⊥AC于点D,则BD的长为( )
A.0.8 B.1.6
C.3.2 D.4.8
4.一直角三角形的三边分别为2、3、x,那么以x为边长的正方形的面积为( )
A.13 B.5 C.13或5 D.4
5.下列各数组中,不能作为直角三角形三边长的是 ( )
A. 9,12,15 B. 7,24,25 C. 6,8,10 D. 3,5,7
6、在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.
(1)若a=7,b=24,求c (2)若c=15,b=12,求a (3)若a∶b=3∶4,c=10,求a,b
7、如图8,某人划船横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B 5 m,结果他在水中实际划了13 m,求该河流的宽度.
8、如图12,在△ABC中,AC⊥BC,AE平分∠BAC交BC于点E,DE⊥AB于点D,BC=12 cm,AC=5 cm,求BE的长.
9.如图,在△ABC中,∠ACB=90°,BC=6,AC=8,CD是高.
(1)求AB的长;
(2)求△ABC的面积;
(3)求CD的长.
二、选做题
10.一等腰三角形底边长为10cm,腰长为13cm,则腰上的高为 ( )
A. 12cm B. C. D.
11.如图所示,,,,求正方形的面积.
三、拓展题
12. 如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE丄DF,交AB于E,交BC于F,若AE=4,FC=3,求EF长.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
