2024人教版高中数学必修第二册同步练习题--8.1 基本立体图形-第1课时(含解析)
文档属性
| 名称 | 2024人教版高中数学必修第二册同步练习题--8.1 基本立体图形-第1课时(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024人教版高中数学必修第二册同步练习题
第八章 立体几何初步
8.1 基本立体图形
第1课时 棱柱、棱锥、棱台
基础过关练
题组一 棱柱
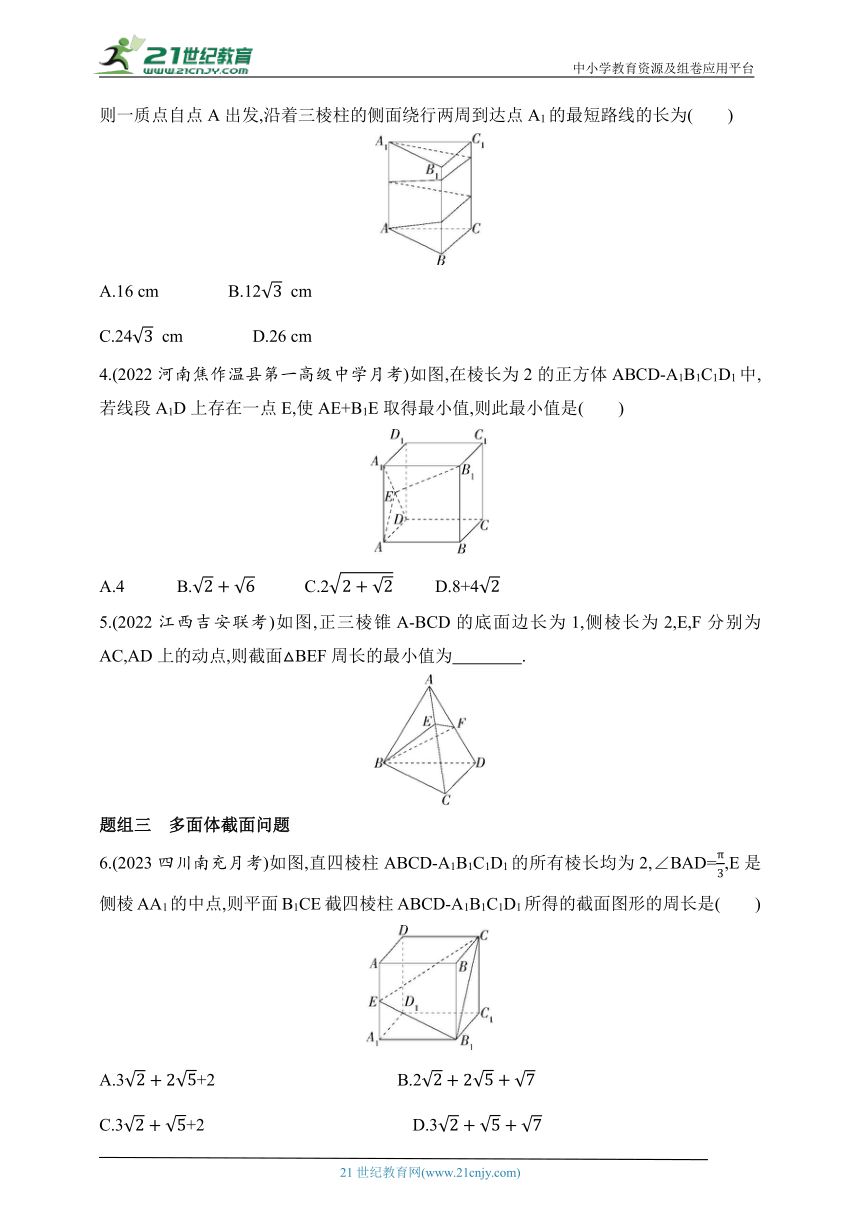
1.下列几何体中棱柱有( )
A.3个 B.4个 C.5个 D.6个
2.(2022浙江杭州西湖高级中学期中)如图,将装有水的长方体水槽固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形成的几何体是( )
A.棱柱
B.棱台
C.棱柱与棱锥的组合体
D.不能确定
题组二 棱锥
3.下列几何体中不是棱锥的为( )
4.(2023福建三明一中月考)如图所示,在三棱台ABC-A'B'C'中,沿平面A'BC截去三棱锥A'-ABC,则剩余的部分是( )
A.三棱锥 B.四棱锥 C.三棱柱 D.组合体
5.(多选题)(2023河南安阳林州一中期末)某人用如图所示的纸片沿折痕折后粘成一个四棱锥形的“走马灯”,正方形作灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则①②③处的字可能为( )
A.乐、新、快 B.快、新、乐
C.新、快、乐 D.乐、快、新
题组三 棱台
6.棱台不具备的特点是( )
A.两底面相似 B.侧面都是梯形
C.侧棱都相等 D.侧棱所在直线都交于一点
7.(2022山西运城期中)如图,在三棱柱ABC-A1B1C1中,E,F分别是A1B1,A1C1的中点,连接BE,EF,FC,试判断几何体A1EF-ABC是什么几何体,并指出它的底面与侧面.
能力提升练
题组一 多面体中的计算问题
1.一个棱锥被平行于底面的平面所截,如果截面面积与底面面积之比为1∶2,则截面把棱锥的一条侧棱分成的两段之比是( )
A.1∶4 B.1∶2
C.1∶(-1) D.1∶(+1)
2.已知正四棱锥S-ABCD的高为,侧棱长为.
(1)求正四棱锥S-ABCD的斜高;
(2)求一个侧面的面积;
(3)求底面的面积.
题组二 与多面体表面展开图有关的问题
3.(2023上海晋元高级中学期末)已知正三棱柱ABC-A1B1C1的底面边长为4 cm,高为10 cm,则一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为( )
A.16 cm B.12 cm
C.24 cm D.26 cm
4.(2022河南焦作温县第一高级中学月考)如图,在棱长为2的正方体ABCD-A1B1C1D1中,若线段A1D上存在一点E,使AE+B1E取得最小值,则此最小值是( )
A.4 B.C.2D.8+4
5.(2022江西吉安联考)如图,正三棱锥A-BCD的底面边长为1,侧棱长为2,E,F分别为AC,AD上的动点,则截面△BEF周长的最小值为 .
题组三 多面体截面问题
6.(2023四川南充月考)如图,直四棱柱ABCD-A1B1C1D1的所有棱长均为2,∠BAD=,E是侧棱AA1的中点,则平面B1CE截四棱柱ABCD-A1B1C1D1所得的截面图形的周长是( )
A.3+2 B.2
C.3+2 D.3
7.(2022湖南株洲一检)已知三棱锥D-ABC的各棱长均为1,且其四个顶点都在球O的球面上.若过球心O的一个截面如图所示,则该截面中三角形(阴影部分)的面积为 .
答案与分层梯度式解析
基础过关练
1.C 2.A 3.A 4.B 5.BC 6.C
1.C 根据棱柱的定义,知①②③④⑤中的几何体是棱柱,共5个.
方法归纳 判断一个几何体是不是棱柱,关键是看这个几何体是否满足棱柱的定义:①看“面”,即观察这个多面体是否有两个互相平行的面,且其余各面都是四边形;②看“线”,即观察相邻两个四边形的公共边是否都互相平行.
2.A 因为有水的部分前后两个面平行,其余各面都是平行四边形,所以水形成的几何体是棱柱.
3.A
4.B 剩余的部分是四棱锥A'-BCC'B'.故选B.
5.BC 题图中四个三角形为四棱锥的侧面,由四棱锥的结构特征知,正好看到“新年快乐”的字样的顺序可以是①年②③,②年①③,即①②③处可依次为新、快、乐或快、新、乐.
故选BC.
6.C 因为棱锥的侧棱不一定相等,所以截得棱台的侧棱也不一定相等.
7.解析 ∵E,F分别是A1B1,A1C1的中点,且A1B1=AB,A1C1=AC,B1C1=BC,
∴.
∴△A1EF∽△ABC,且AA1,BE,CF延长后交于一点.
又面A1EF与面ABC平行,
∴几何体A1EF-ABC是三棱台,面ABC是下底面,面A1EF是上底面,面ABEA1,面BCFE和面ACFA1是侧面.
能力提升练
1.C 3.D 4.C 6.D
1.C 设截后所得小棱锥的侧棱长为l,原棱锥的侧棱长为L,
一个棱锥被平行于底面的平面所截,则截面与底面相似,若截面面积与底面面积之比为1∶2,
则,故.
∴截面把棱锥的一条侧棱分成的两段之比是1∶(-1).故选C.
2.解析 (1)如图,连接AC,BD,交于点O,连接SO,则SO是正四棱锥的高.取BC的中点M,连接OM,SM,则SM为正四棱锥的斜高.
在Rt△SBO中,OB==2,
∴AB=2,故OM=,则SM=.
(2)∵BC=AB=2,∴S△SBC=BC·SM=,即一个侧面的面积为.
(3)底面ABCD的面积为AB2=(2)2=8.
导师点睛 在正棱锥的计算问题中要善于应用由高、斜高、斜高在底面上的射影构成的直角三角形和由高、侧棱、侧棱在底面上的射影构成的直角三角形.
3.D 将正三棱柱ABC-A1B1C1沿侧棱AA1展开,再拼接一次(因为绕行两周,所以需要再拼接一次),如图所示,
所求最短路线的长即为六个小矩形拼成的矩形的对角线的长度,易得拼成的矩形的长为6×4=24 cm,宽为10 cm,
所以最短路线的长为=26 cm.
4.C 连接B1C(动线段B1E始终在四边形A1B1CD内),将△AA1D沿A1D所在直线翻折,使点A与四边形A1B1CD构成如图所示的平面图形,(将立体问题转化为平面问题)
连接AB1,因为E是线段A1D上任意一点,所以AE+B1E≥AB1,当且仅当A,E,B1三点共线时,等号成立,故所求最小值为|AB1|,
在△AA1B1中,由余弦定理得A-2AA1 · A1B1cos(45°+90°)=8+4,所以AB1=.
故选C.
5.答案
解析 正三棱锥A-BCD的侧面展开图如图所示:
若截面△BEF的周长最小,则B,E,F,B'共线,即周长的最小值为|BB'|.
易知BB'∥CD,∴∠B'FD=∠ADC=∠ADB',
∴B'F=B'D=1,
同理可得BE=BC=1.
∵∠B'FD=∠ADB'=∠AB'D,∠ADB'=∠B'DF,
∴△ADB'∽△B'DF,
∴,∴DF=,∴AF=,
∵EF∥CD,∴,∴EF=,
∴BB'=BE+EF+B'F=1+.
6.D 延长B1E,交BA的延长线于点F, 连接CF,交AD于点G,连接EG,如图.
因为AE=BB1,AE∥BB1 ,所以A为BF的中点,
则G为CF,AD的中点,故GE∥B1C,
所以截面为梯形B1CGE.
易得B1C=,
由∠BAD=,可得∠CDG=,
故CG=
=,
故梯形B1CGE的周长为3.
故选D.
主编点评 作截面的步骤:
(1)确定截面与多面体的哪些棱相交;
(2)找到截面与多面体相交棱的公共点;
(3)将所得的公共点依次连接起来,即得截面.
7.答案
解析 根据题意,过该球球心的一个截面经过正三棱锥的一条棱,
由球的对称性可得球心在该正三棱锥的高上,
所以截面是三棱锥的一条棱与高线所在的平面,故截面中三角形即为这条棱和与其相对棱的中点构成的三角形,
如图,在正三棱锥D-ABC中,设截面中的三角形为△BDF,其中F为棱AC的中点,
因为三棱锥D-ABC的各棱长均为1,
所以BF=DF=,
取BD的中点E,连接EF,则EF为等腰三角形BDF底边BD上的高,
EF=,
所以S△BDF=,
即该截面中三角形(阴影部分)的面积为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版高中数学必修第二册同步练习题
第八章 立体几何初步
8.1 基本立体图形
第1课时 棱柱、棱锥、棱台
基础过关练
题组一 棱柱
1.下列几何体中棱柱有( )
A.3个 B.4个 C.5个 D.6个
2.(2022浙江杭州西湖高级中学期中)如图,将装有水的长方体水槽固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形成的几何体是( )
A.棱柱
B.棱台
C.棱柱与棱锥的组合体
D.不能确定
题组二 棱锥
3.下列几何体中不是棱锥的为( )
4.(2023福建三明一中月考)如图所示,在三棱台ABC-A'B'C'中,沿平面A'BC截去三棱锥A'-ABC,则剩余的部分是( )
A.三棱锥 B.四棱锥 C.三棱柱 D.组合体
5.(多选题)(2023河南安阳林州一中期末)某人用如图所示的纸片沿折痕折后粘成一个四棱锥形的“走马灯”,正方形作灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则①②③处的字可能为( )
A.乐、新、快 B.快、新、乐
C.新、快、乐 D.乐、快、新
题组三 棱台
6.棱台不具备的特点是( )
A.两底面相似 B.侧面都是梯形
C.侧棱都相等 D.侧棱所在直线都交于一点
7.(2022山西运城期中)如图,在三棱柱ABC-A1B1C1中,E,F分别是A1B1,A1C1的中点,连接BE,EF,FC,试判断几何体A1EF-ABC是什么几何体,并指出它的底面与侧面.
能力提升练
题组一 多面体中的计算问题
1.一个棱锥被平行于底面的平面所截,如果截面面积与底面面积之比为1∶2,则截面把棱锥的一条侧棱分成的两段之比是( )
A.1∶4 B.1∶2
C.1∶(-1) D.1∶(+1)
2.已知正四棱锥S-ABCD的高为,侧棱长为.
(1)求正四棱锥S-ABCD的斜高;
(2)求一个侧面的面积;
(3)求底面的面积.
题组二 与多面体表面展开图有关的问题
3.(2023上海晋元高级中学期末)已知正三棱柱ABC-A1B1C1的底面边长为4 cm,高为10 cm,则一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为( )
A.16 cm B.12 cm
C.24 cm D.26 cm
4.(2022河南焦作温县第一高级中学月考)如图,在棱长为2的正方体ABCD-A1B1C1D1中,若线段A1D上存在一点E,使AE+B1E取得最小值,则此最小值是( )
A.4 B.C.2D.8+4
5.(2022江西吉安联考)如图,正三棱锥A-BCD的底面边长为1,侧棱长为2,E,F分别为AC,AD上的动点,则截面△BEF周长的最小值为 .
题组三 多面体截面问题
6.(2023四川南充月考)如图,直四棱柱ABCD-A1B1C1D1的所有棱长均为2,∠BAD=,E是侧棱AA1的中点,则平面B1CE截四棱柱ABCD-A1B1C1D1所得的截面图形的周长是( )
A.3+2 B.2
C.3+2 D.3
7.(2022湖南株洲一检)已知三棱锥D-ABC的各棱长均为1,且其四个顶点都在球O的球面上.若过球心O的一个截面如图所示,则该截面中三角形(阴影部分)的面积为 .
答案与分层梯度式解析
基础过关练
1.C 2.A 3.A 4.B 5.BC 6.C
1.C 根据棱柱的定义,知①②③④⑤中的几何体是棱柱,共5个.
方法归纳 判断一个几何体是不是棱柱,关键是看这个几何体是否满足棱柱的定义:①看“面”,即观察这个多面体是否有两个互相平行的面,且其余各面都是四边形;②看“线”,即观察相邻两个四边形的公共边是否都互相平行.
2.A 因为有水的部分前后两个面平行,其余各面都是平行四边形,所以水形成的几何体是棱柱.
3.A
4.B 剩余的部分是四棱锥A'-BCC'B'.故选B.
5.BC 题图中四个三角形为四棱锥的侧面,由四棱锥的结构特征知,正好看到“新年快乐”的字样的顺序可以是①年②③,②年①③,即①②③处可依次为新、快、乐或快、新、乐.
故选BC.
6.C 因为棱锥的侧棱不一定相等,所以截得棱台的侧棱也不一定相等.
7.解析 ∵E,F分别是A1B1,A1C1的中点,且A1B1=AB,A1C1=AC,B1C1=BC,
∴.
∴△A1EF∽△ABC,且AA1,BE,CF延长后交于一点.
又面A1EF与面ABC平行,
∴几何体A1EF-ABC是三棱台,面ABC是下底面,面A1EF是上底面,面ABEA1,面BCFE和面ACFA1是侧面.
能力提升练
1.C 3.D 4.C 6.D
1.C 设截后所得小棱锥的侧棱长为l,原棱锥的侧棱长为L,
一个棱锥被平行于底面的平面所截,则截面与底面相似,若截面面积与底面面积之比为1∶2,
则,故.
∴截面把棱锥的一条侧棱分成的两段之比是1∶(-1).故选C.
2.解析 (1)如图,连接AC,BD,交于点O,连接SO,则SO是正四棱锥的高.取BC的中点M,连接OM,SM,则SM为正四棱锥的斜高.
在Rt△SBO中,OB==2,
∴AB=2,故OM=,则SM=.
(2)∵BC=AB=2,∴S△SBC=BC·SM=,即一个侧面的面积为.
(3)底面ABCD的面积为AB2=(2)2=8.
导师点睛 在正棱锥的计算问题中要善于应用由高、斜高、斜高在底面上的射影构成的直角三角形和由高、侧棱、侧棱在底面上的射影构成的直角三角形.
3.D 将正三棱柱ABC-A1B1C1沿侧棱AA1展开,再拼接一次(因为绕行两周,所以需要再拼接一次),如图所示,
所求最短路线的长即为六个小矩形拼成的矩形的对角线的长度,易得拼成的矩形的长为6×4=24 cm,宽为10 cm,
所以最短路线的长为=26 cm.
4.C 连接B1C(动线段B1E始终在四边形A1B1CD内),将△AA1D沿A1D所在直线翻折,使点A与四边形A1B1CD构成如图所示的平面图形,(将立体问题转化为平面问题)
连接AB1,因为E是线段A1D上任意一点,所以AE+B1E≥AB1,当且仅当A,E,B1三点共线时,等号成立,故所求最小值为|AB1|,
在△AA1B1中,由余弦定理得A-2AA1 · A1B1cos(45°+90°)=8+4,所以AB1=.
故选C.
5.答案
解析 正三棱锥A-BCD的侧面展开图如图所示:
若截面△BEF的周长最小,则B,E,F,B'共线,即周长的最小值为|BB'|.
易知BB'∥CD,∴∠B'FD=∠ADC=∠ADB',
∴B'F=B'D=1,
同理可得BE=BC=1.
∵∠B'FD=∠ADB'=∠AB'D,∠ADB'=∠B'DF,
∴△ADB'∽△B'DF,
∴,∴DF=,∴AF=,
∵EF∥CD,∴,∴EF=,
∴BB'=BE+EF+B'F=1+.
6.D 延长B1E,交BA的延长线于点F, 连接CF,交AD于点G,连接EG,如图.
因为AE=BB1,AE∥BB1 ,所以A为BF的中点,
则G为CF,AD的中点,故GE∥B1C,
所以截面为梯形B1CGE.
易得B1C=,
由∠BAD=,可得∠CDG=,
故CG=
=,
故梯形B1CGE的周长为3.
故选D.
主编点评 作截面的步骤:
(1)确定截面与多面体的哪些棱相交;
(2)找到截面与多面体相交棱的公共点;
(3)将所得的公共点依次连接起来,即得截面.
7.答案
解析 根据题意,过该球球心的一个截面经过正三棱锥的一条棱,
由球的对称性可得球心在该正三棱锥的高上,
所以截面是三棱锥的一条棱与高线所在的平面,故截面中三角形即为这条棱和与其相对棱的中点构成的三角形,
如图,在正三棱锥D-ABC中,设截面中的三角形为△BDF,其中F为棱AC的中点,
因为三棱锥D-ABC的各棱长均为1,
所以BF=DF=,
取BD的中点E,连接EF,则EF为等腰三角形BDF底边BD上的高,
EF=,
所以S△BDF=,
即该截面中三角形(阴影部分)的面积为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
