2024人教版高中数学必修第二册同步练习题--8.1 基本立体图形-第2课时(含解析)
文档属性
| 名称 | 2024人教版高中数学必修第二册同步练习题--8.1 基本立体图形-第2课时(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024人教版高中数学必修第二册同步练习题
第2课时 圆柱、圆锥、圆台与球
基础过关练
题组一 圆柱、圆锥、圆台
1.(2022山东泰安期中)在直角梯形ABCD中,,∠BAD=,以AD所在的直线为轴,其余三边旋转一周形成的面所围成的几何体为 ( )
A.棱台 B.圆台 C.圆柱 D.四棱柱
2.用一个平面去截圆锥,则截面不可能是( )
A.椭圆 B.圆 C.三角形 D.矩形
3.(2023上海静安期末)把一个圆锥截成圆台,已知圆台的上、下底面半径的比为1∶4,母线长为9,则原圆锥的母线长为 .
4.圆柱的母线长为5,底面半径为2,则该圆柱的轴截面的面积为 .
题组二 球
5.截一个几何体,各个截面都是圆面,则这个几何体一定是( )
A.圆柱 B.圆锥 C.球 D.圆台
6.下列说法正确的是( )
A.到定点的距离等于定长的点的集合是球
B.球面上不同的三点可能在同一条直线上
C.球的直径可以是球面上任意两点所连的线段
D.球心与截面圆心(截面不过球心)的连线垂直于该截面
7.(2022北京海淀实验中学期末)已知球O的半径为2,球心到平面α的距离为,则球O被平面α截得的截面面积为( )
A.π B.π C.3π D.2π
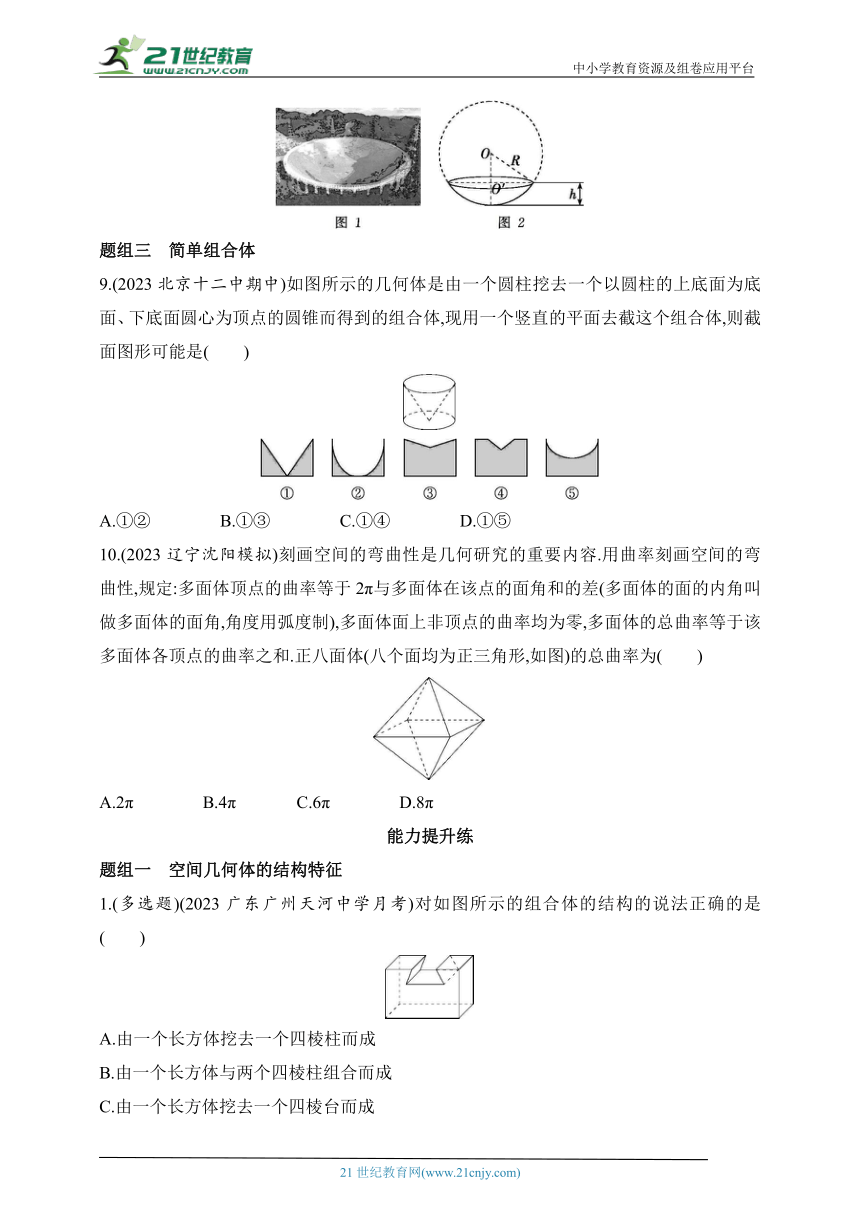
8.(2023山东滨州期末)“中国天眼”(如图1)是目前世界上最大、最灵敏的单口径射电望远镜,其形状可近似地看成一个球冠,球冠是球面被平面所截的一部分,如图2所示,截得的圆面叫做球冠的底,垂直于截面的直径被截得的线段叫做球冠的高.若球面的半径是R,球冠的高度是h,则球冠的面积S=2πRh.已知“中国天眼”的底的半径约为250米,反射面面积(球冠面积)约为25万平方米,则“中国天眼”的高度约为
米.参考数据:≈0.52
题组三 简单组合体
9.(2023北京十二中期中)如图所示的几何体是由一个圆柱挖去一个以圆柱的上底面为底面、下底面圆心为顶点的圆锥而得到的组合体,现用一个竖直的平面去截这个组合体,则截面图形可能是( )
A.①② B.①③ C.①④ D.①⑤
10.(2023辽宁沈阳模拟)刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间的弯曲性,规定:多面体顶点的曲率等于2π与多面体在该点的面角和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.正八面体(八个面均为正三角形,如图)的总曲率为( )
A.2π B.4π C.6π D.8π
能力提升练
题组一 空间几何体的结构特征
1.(多选题)(2023广东广州天河中学月考)对如图所示的组合体的结构的说法正确的是( )
A.由一个长方体挖去一个四棱柱而成
B.由一个长方体与两个四棱柱组合而成
C.由一个长方体挖去一个四棱台而成
D.由一个长方体与两个四棱台组合而成
2.(2022上海华东师范大学第一附属中学期末)半正多面体是由两种或两种以上的正多边形围成的多面体.下图是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1,则该半正多面体共有面的个数及棱长分别为( )
A.26,-1 B.24,2-
C.26,2-D.24,-1
题组二 与旋转体表面展开图有关的问题
3.(2022河北张家口月考)如图,圆锥的母线AB的长为2,底面圆的半径为r,若一只蚂蚁从圆锥上的点B出发,沿表面爬到母线AC的中点D处,爬行的最短路线长为,则r=( )
A.1 B.2 C.3 D.
4.(2022河北沧州开学考试)如图所示,圆柱的高为2,底面半径为1,则在圆柱侧面上从A出发经过母线BB1到达A1的最短距离为 .
题组三 旋转体中的计算问题
5.(2022云南师大附中期中)在直角三角形ABC中,已知AC=2,BC=2,C=90°,以AC所在直线为旋转轴将△ABC旋转一周,AB、BC边形成的面所围成的旋转体是一个圆锥,则经过该圆锥任意两条母线的截面三角形的面积的最大值为( )
A.4 D.8
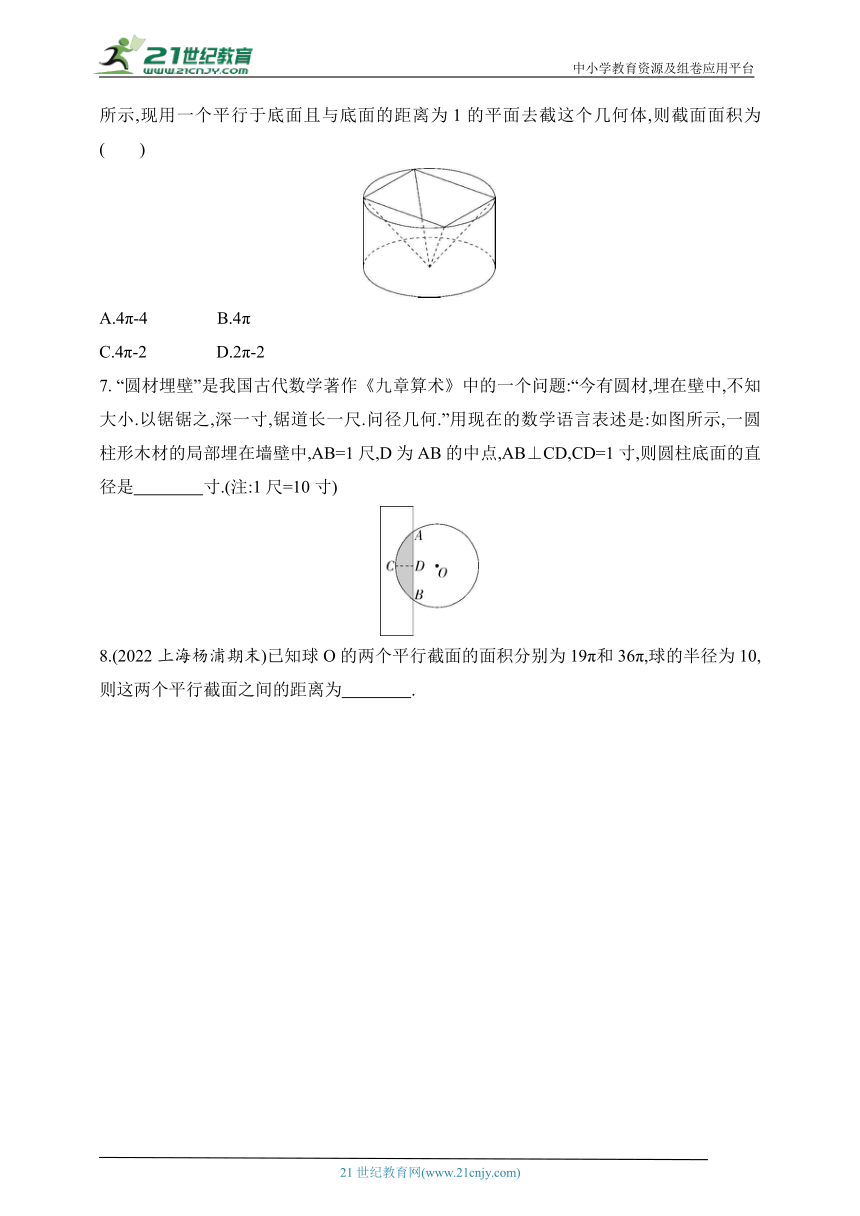
6.(2022湖湘教育三新探索协作体期中)从一个底面半径与高均为2的圆柱中挖去一个正四棱锥(以圆柱的上底面为正四棱锥底面的外接圆,下底面圆心为顶点)得到的几何体如图所示,现用一个平行于底面且与底面的距离为1的平面去截这个几何体,则截面面积为( )
A.4π-4 B.4π
C.4π-2 D.2π-2
7. “圆材埋壁”是我国古代数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何.”用现在的数学语言表述是:如图所示,一圆柱形木材的局部埋在墙壁中,AB=1尺,D为AB的中点,AB⊥CD,CD=1寸,则圆柱底面的直径是 寸.(注:1尺=10寸)
8.(2022上海杨浦期末)已知球O的两个平行截面的面积分别为19π和36π,球的半径为10,则这两个平行截面之间的距离为 .
答案与分层梯度式解析
基础过关练
1.B 2.D 5.C 6.D 7.A 9.D 10.B
1.B
2.D 用一个不平行于圆锥底面的平面去截圆锥,截面可能为椭圆;
用一个平行于圆锥底面的平面去截圆锥,截面为圆;
用一个过圆锥的轴的平面去截圆锥,截面为等腰三角形.故选D.
3.答案 12
解析 如图,由题意可知,,BD=9,
设原圆锥的母线长为l,根据相似三角形的性质可得,即,解得l=12,故原圆锥的母线长为12.
4.答案 20
解析 易知该圆柱的轴截面为矩形,矩形的两邻边长分别为5和4,故轴截面的面积为5×4=20.
5.C 圆柱的截面可能是矩形,圆锥的截面可能是三角形,圆台的截面可能是梯形,故选C.
6.D 对于A,球是球体的简称,球体的外表面称为球面,球面是一个曲面,是空心的,而球是几何体,是实心的,故A错;对于B,球面上不同的三点一定不共线,故B错;对于C,球的直径必过球心,故C错.故选D.
7.A 设截面圆的半径为r,则r==1,
所以球O被平面α截得的截面面积为πr2=π.
故选A.
8.答案 130
解析 由题意得(R-h)2+2502=R2,
则2Rh=h2+2502,
故2πRh=πh2+2502π=250 000,
所以h2=,
所以h=250≈250×0.52=130.
9.D 当截面过底面直径时,截面如题图①;当截面不过底面直径时,截面如题图⑤.故选D.
10.B 正八面体共有6个顶点,每个面均为等边三角形,且每个面的面角和为π,
因此,该正八面体的总曲率为6×2π-8π=4π.
故选B.
能力提升练
1.AB 2.A 3.A 5.D 6.C
1.AB 该组合体可由一个长方体挖去一个四棱柱而成,也可以由一个长方体与两个四棱柱组合而成.故选AB.
2.A 半正多面体面数从上至下依次为1,8,8,8,1,故共有1+8+8+8+1=26个面.如图1,正方体被半正多面体顶点A,B,C所在平面所截,截得的图形如图2,八边形ABCDEFGH为正八边形.
设AB=a,则1=2×a+a,
解得a=-1,
即该半正多面体的棱长为-1.
故选A.
3.A 半圆锥的侧面展开图如图,
易知BD的长为蚂蚁爬行的最短路线长,
由题意得BD=,AD=1,AB=2,
在△ABD中,AB2+AD2=BD2,
所以∠DAB=,
所以l×2=π,
所以圆锥底面圆的周长为2l =2π,故2πr=2π,解得r=1.故选A.
4.答案 2
解析 将圆柱侧面沿母线AA1展开,如图,连接AA'1,则所求最短距离为AA'1的长.
易得AA'=2π×1=2π,
故AA'1=.
5.D 如图,
若AB和AD为圆锥的两条母线,则截面为等腰三角形ABD,
∴截面面积为S△ABD=AB·AD·sin∠BAD.
∵AD=AB==4,是定值,
∴当sin∠BAD最大时截面面积最大.
由图可知,当截面为圆锥的轴截面时,∠BAD最大,为120°,
∴0°<∠BAD≤120°,∴sin∠BAD的最大值为1.
故截面面积最大为×42×1=8.故选D.
6.C 截面应为圆面中挖去一个正方形,且圆的半径是2,面积为4π.
设正四棱锥的底面正方形的边长为a,易知a=2,
故正四棱锥的底面正方形的面积为(2)2=8,
由棱锥中截面的性质,可得圆面中挖去的正方形与正四棱锥的底面正方形相似,设圆面中挖去的正方形的面积为S',正四棱锥的底面正方形的面积为S,
则,从而S'=2,
所以截面的面积为4π-2.
故选C.
7.答案 26
解析 连接OA,OD,
∵D为AB的中点,∴OD⊥AB,
又AB⊥CD,∴C,D,O三点共线,
∵AB=10寸,∴AD=5寸,
在Rt△AOD中,
∵OA2=OD2+AD2,
∴OA2=(OA-1)2+52,
∴OA=13寸,
∴圆柱底面的直径是2OA=26寸.
8.答案 1或17
解析 因为球O的两个平行截面的面积分别为19π和36π,
所以这两个平行截面的半径分别为和6,
则球心到两个平行截面的距离分别为=8.
当两个平行截面在球心O的同侧时,如图所示:
则这两个平行截面之间的距离为|O1O2|=9-8=1;
当两个平行截面在球心O的两侧时,如图所示:
则这两个平行截面之间的距离为|O1O2|=9+8=17.
故答案为1或17.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版高中数学必修第二册同步练习题
第2课时 圆柱、圆锥、圆台与球
基础过关练
题组一 圆柱、圆锥、圆台
1.(2022山东泰安期中)在直角梯形ABCD中,,∠BAD=,以AD所在的直线为轴,其余三边旋转一周形成的面所围成的几何体为 ( )
A.棱台 B.圆台 C.圆柱 D.四棱柱
2.用一个平面去截圆锥,则截面不可能是( )
A.椭圆 B.圆 C.三角形 D.矩形
3.(2023上海静安期末)把一个圆锥截成圆台,已知圆台的上、下底面半径的比为1∶4,母线长为9,则原圆锥的母线长为 .
4.圆柱的母线长为5,底面半径为2,则该圆柱的轴截面的面积为 .
题组二 球
5.截一个几何体,各个截面都是圆面,则这个几何体一定是( )
A.圆柱 B.圆锥 C.球 D.圆台
6.下列说法正确的是( )
A.到定点的距离等于定长的点的集合是球
B.球面上不同的三点可能在同一条直线上
C.球的直径可以是球面上任意两点所连的线段
D.球心与截面圆心(截面不过球心)的连线垂直于该截面
7.(2022北京海淀实验中学期末)已知球O的半径为2,球心到平面α的距离为,则球O被平面α截得的截面面积为( )
A.π B.π C.3π D.2π
8.(2023山东滨州期末)“中国天眼”(如图1)是目前世界上最大、最灵敏的单口径射电望远镜,其形状可近似地看成一个球冠,球冠是球面被平面所截的一部分,如图2所示,截得的圆面叫做球冠的底,垂直于截面的直径被截得的线段叫做球冠的高.若球面的半径是R,球冠的高度是h,则球冠的面积S=2πRh.已知“中国天眼”的底的半径约为250米,反射面面积(球冠面积)约为25万平方米,则“中国天眼”的高度约为
米.参考数据:≈0.52
题组三 简单组合体
9.(2023北京十二中期中)如图所示的几何体是由一个圆柱挖去一个以圆柱的上底面为底面、下底面圆心为顶点的圆锥而得到的组合体,现用一个竖直的平面去截这个组合体,则截面图形可能是( )
A.①② B.①③ C.①④ D.①⑤
10.(2023辽宁沈阳模拟)刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间的弯曲性,规定:多面体顶点的曲率等于2π与多面体在该点的面角和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.正八面体(八个面均为正三角形,如图)的总曲率为( )
A.2π B.4π C.6π D.8π
能力提升练
题组一 空间几何体的结构特征
1.(多选题)(2023广东广州天河中学月考)对如图所示的组合体的结构的说法正确的是( )
A.由一个长方体挖去一个四棱柱而成
B.由一个长方体与两个四棱柱组合而成
C.由一个长方体挖去一个四棱台而成
D.由一个长方体与两个四棱台组合而成
2.(2022上海华东师范大学第一附属中学期末)半正多面体是由两种或两种以上的正多边形围成的多面体.下图是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1,则该半正多面体共有面的个数及棱长分别为( )
A.26,-1 B.24,2-
C.26,2-D.24,-1
题组二 与旋转体表面展开图有关的问题
3.(2022河北张家口月考)如图,圆锥的母线AB的长为2,底面圆的半径为r,若一只蚂蚁从圆锥上的点B出发,沿表面爬到母线AC的中点D处,爬行的最短路线长为,则r=( )
A.1 B.2 C.3 D.
4.(2022河北沧州开学考试)如图所示,圆柱的高为2,底面半径为1,则在圆柱侧面上从A出发经过母线BB1到达A1的最短距离为 .
题组三 旋转体中的计算问题
5.(2022云南师大附中期中)在直角三角形ABC中,已知AC=2,BC=2,C=90°,以AC所在直线为旋转轴将△ABC旋转一周,AB、BC边形成的面所围成的旋转体是一个圆锥,则经过该圆锥任意两条母线的截面三角形的面积的最大值为( )
A.4 D.8
6.(2022湖湘教育三新探索协作体期中)从一个底面半径与高均为2的圆柱中挖去一个正四棱锥(以圆柱的上底面为正四棱锥底面的外接圆,下底面圆心为顶点)得到的几何体如图所示,现用一个平行于底面且与底面的距离为1的平面去截这个几何体,则截面面积为( )
A.4π-4 B.4π
C.4π-2 D.2π-2
7. “圆材埋壁”是我国古代数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何.”用现在的数学语言表述是:如图所示,一圆柱形木材的局部埋在墙壁中,AB=1尺,D为AB的中点,AB⊥CD,CD=1寸,则圆柱底面的直径是 寸.(注:1尺=10寸)
8.(2022上海杨浦期末)已知球O的两个平行截面的面积分别为19π和36π,球的半径为10,则这两个平行截面之间的距离为 .
答案与分层梯度式解析
基础过关练
1.B 2.D 5.C 6.D 7.A 9.D 10.B
1.B
2.D 用一个不平行于圆锥底面的平面去截圆锥,截面可能为椭圆;
用一个平行于圆锥底面的平面去截圆锥,截面为圆;
用一个过圆锥的轴的平面去截圆锥,截面为等腰三角形.故选D.
3.答案 12
解析 如图,由题意可知,,BD=9,
设原圆锥的母线长为l,根据相似三角形的性质可得,即,解得l=12,故原圆锥的母线长为12.
4.答案 20
解析 易知该圆柱的轴截面为矩形,矩形的两邻边长分别为5和4,故轴截面的面积为5×4=20.
5.C 圆柱的截面可能是矩形,圆锥的截面可能是三角形,圆台的截面可能是梯形,故选C.
6.D 对于A,球是球体的简称,球体的外表面称为球面,球面是一个曲面,是空心的,而球是几何体,是实心的,故A错;对于B,球面上不同的三点一定不共线,故B错;对于C,球的直径必过球心,故C错.故选D.
7.A 设截面圆的半径为r,则r==1,
所以球O被平面α截得的截面面积为πr2=π.
故选A.
8.答案 130
解析 由题意得(R-h)2+2502=R2,
则2Rh=h2+2502,
故2πRh=πh2+2502π=250 000,
所以h2=,
所以h=250≈250×0.52=130.
9.D 当截面过底面直径时,截面如题图①;当截面不过底面直径时,截面如题图⑤.故选D.
10.B 正八面体共有6个顶点,每个面均为等边三角形,且每个面的面角和为π,
因此,该正八面体的总曲率为6×2π-8π=4π.
故选B.
能力提升练
1.AB 2.A 3.A 5.D 6.C
1.AB 该组合体可由一个长方体挖去一个四棱柱而成,也可以由一个长方体与两个四棱柱组合而成.故选AB.
2.A 半正多面体面数从上至下依次为1,8,8,8,1,故共有1+8+8+8+1=26个面.如图1,正方体被半正多面体顶点A,B,C所在平面所截,截得的图形如图2,八边形ABCDEFGH为正八边形.
设AB=a,则1=2×a+a,
解得a=-1,
即该半正多面体的棱长为-1.
故选A.
3.A 半圆锥的侧面展开图如图,
易知BD的长为蚂蚁爬行的最短路线长,
由题意得BD=,AD=1,AB=2,
在△ABD中,AB2+AD2=BD2,
所以∠DAB=,
所以l×2=π,
所以圆锥底面圆的周长为2l =2π,故2πr=2π,解得r=1.故选A.
4.答案 2
解析 将圆柱侧面沿母线AA1展开,如图,连接AA'1,则所求最短距离为AA'1的长.
易得AA'=2π×1=2π,
故AA'1=.
5.D 如图,
若AB和AD为圆锥的两条母线,则截面为等腰三角形ABD,
∴截面面积为S△ABD=AB·AD·sin∠BAD.
∵AD=AB==4,是定值,
∴当sin∠BAD最大时截面面积最大.
由图可知,当截面为圆锥的轴截面时,∠BAD最大,为120°,
∴0°<∠BAD≤120°,∴sin∠BAD的最大值为1.
故截面面积最大为×42×1=8.故选D.
6.C 截面应为圆面中挖去一个正方形,且圆的半径是2,面积为4π.
设正四棱锥的底面正方形的边长为a,易知a=2,
故正四棱锥的底面正方形的面积为(2)2=8,
由棱锥中截面的性质,可得圆面中挖去的正方形与正四棱锥的底面正方形相似,设圆面中挖去的正方形的面积为S',正四棱锥的底面正方形的面积为S,
则,从而S'=2,
所以截面的面积为4π-2.
故选C.
7.答案 26
解析 连接OA,OD,
∵D为AB的中点,∴OD⊥AB,
又AB⊥CD,∴C,D,O三点共线,
∵AB=10寸,∴AD=5寸,
在Rt△AOD中,
∵OA2=OD2+AD2,
∴OA2=(OA-1)2+52,
∴OA=13寸,
∴圆柱底面的直径是2OA=26寸.
8.答案 1或17
解析 因为球O的两个平行截面的面积分别为19π和36π,
所以这两个平行截面的半径分别为和6,
则球心到两个平行截面的距离分别为=8.
当两个平行截面在球心O的同侧时,如图所示:
则这两个平行截面之间的距离为|O1O2|=9-8=1;
当两个平行截面在球心O的两侧时,如图所示:
则这两个平行截面之间的距离为|O1O2|=9+8=17.
故答案为1或17.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
