2024人教版高中数学必修第二册同步练习题--9.2.3 总体集中趋势的估计 9.2.4 总体离散程度的估计(含解析)
文档属性
| 名称 | 2024人教版高中数学必修第二册同步练习题--9.2.3 总体集中趋势的估计 9.2.4 总体离散程度的估计(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024人教版高中数学必修第二册同步练习题
9.2.3 总体集中趋势的估计
9.2.4 总体离散程度的估计
基础过关练
题组一 平均数、中位数、众数
1.(2023安徽九师联盟模拟)在一些比赛中,对评委打分的处理方法一般是去掉一个最高分,去掉一个最低分,然后计算余下评分的平均数作为参赛者的得分.在一次有9位评委参加的赛事中,评委对一名参赛者所打的9个分数,去掉一个最高分,去掉一个最低分后,一定不变的数字特征为( )
A.平均数 B.中位数 C.众数 D.方差
2.(2023上海实验学校月考)某学校艺术节举行弹钢琴比赛,现有21名同学报名参赛,初赛成绩各不相同,取前10名参加决赛,小明同学已经知道了自己的成绩,为了判断自己是否能进入决赛,他还需要知道21名同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
3.(2022河北保定部分学校联考)某商家2021年4月至7月的商品计划销售额和实际销售额(单位:万元)如图所示,则下列说法正确的是( )
A.4月至7月的月平均计划销售额为22万元
B.4月至7月的月平均实际销售额为27万元
C.4月至7月的月实际销售额的中位数为25万元
D.这4个月内,总的计划销售额没有完成
4.(2023山东济南模拟)某射击运动员连续射击5次,命中的环数(环数为整数)形成的一组数据中,中位数为8,唯一的众数为9,极差为3,则该组数据的平均数为( )
A.7.6 B.7.8 C.8 D.8.2
5.(多选题)(2023湖北荆门联考)某单位为了解该单位党员开展学习党史知识活动的情况,随机抽取了30名党员,对他们一周的党史学习时间进行了统计,统计数据如下表.则下列对该单位党员一周的党史学习时间的叙述正确的有( )
党史学习时间 (小时) 7 8 9 10 11
党员人数 4 8 7 6 5
A.众数是8小时
B.第40百分位数为8小时
C.平均数是9小时
D.上四分位数是10小时
6.某工厂生产并销售了30双皮鞋,其中各尺码的销售量如表所示:
皮鞋尺码 (cm) 22 22.5 23 23.5 24 24.5 25
销售量 (双) 1 2 4 14 5 3 1
(1)计算这30双皮鞋尺码的平均数、中位数、众数;
(2)从实际出发,问题(1)中的三种统计量的特征对指导工厂生产有无意义
题组二 频率分布直方图与平均数、中位数、众数
7.(2023四川成都联考)某公司为了解用户对其产品的满意度,从使用该产品的用户中随机调查了100位用户,根据用户对产品的满意度评分,得到如图所示的用户满意度评分的频率分布直方图(同一组中数据用该组区间的中点值作代表).若用户满意度评分的中位数、众数、平均数分别为a分,b分,c分,则( )
A.a8.(多选题)(2023河北承德统考)某水果店为了解本店香蕉的日销售情况,依据过去100天香蕉的日销售量(单位:kg)绘制了如图所示的频率分布直方图,若同一组数据用该组区间的中点值作代表,则下列选项正确的有( )
A.直方图中的a=0.025
B.过去100天香蕉的日销售量的平均数的估计值为52 kg
C.过去100天香蕉的日销售量的众数的估计值为50 kg
D.过去100天香蕉的日销售量的中位数的估计值为55 kg
9.(2022江西临川一中期末)某市共有居民60万人,为了制订合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求图中a的值,并估计该市居民月均用水量不少于3吨的人数;
(2)估计该市居民月均用水量的众数和中位数.
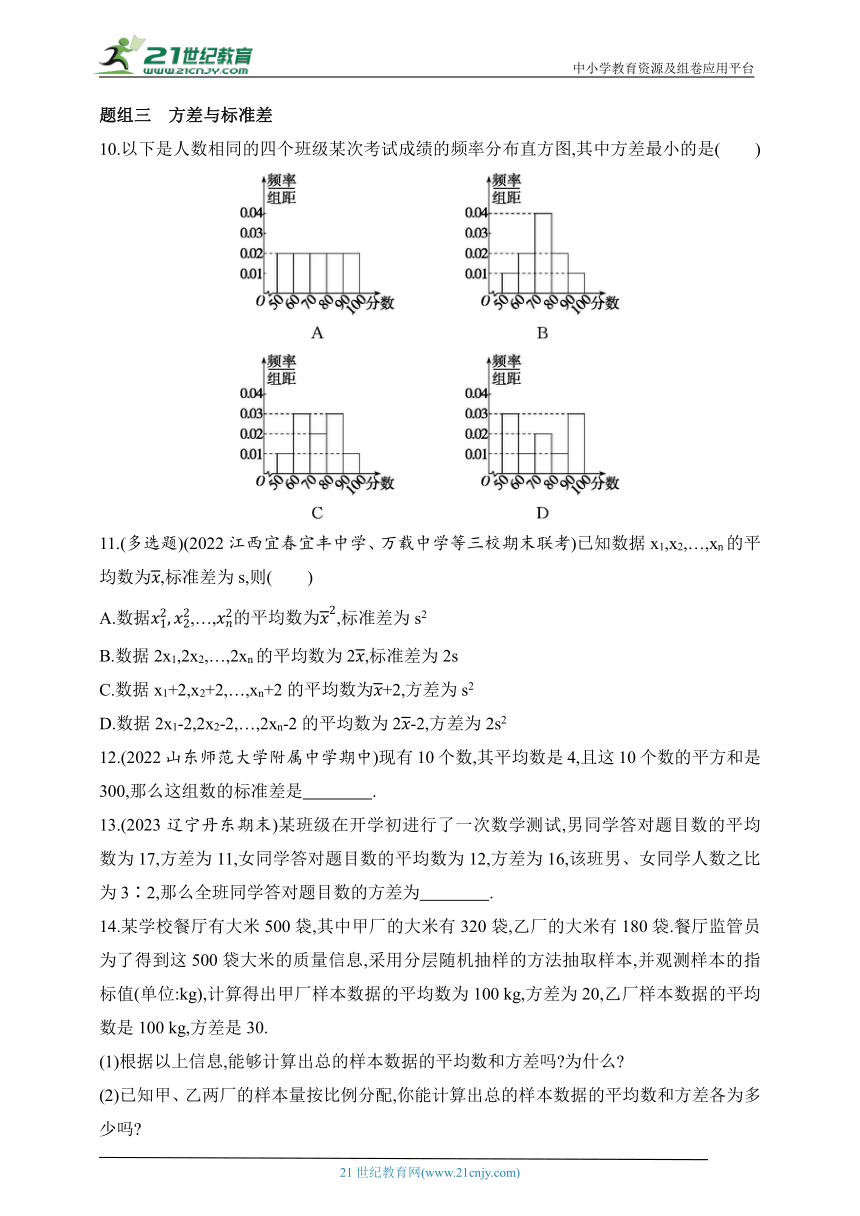
题组三 方差与标准差
10.以下是人数相同的四个班级某次考试成绩的频率分布直方图,其中方差最小的是( )
11.(多选题)(2022江西宜春宜丰中学、万载中学等三校期末联考)已知数据x1,x2,…,xn的平均数为,标准差为s,则( )
A.数据,…,,标准差为s2
B.数据2x1,2x2,…,2xn的平均数为2,标准差为2s
C.数据x1+2,x2+2,…,xn+2的平均数为+2,方差为s2
D.数据2x1-2,2x2-2,…,2xn-2的平均数为2-2,方差为2s2
12.(2022山东师范大学附属中学期中)现有10个数,其平均数是4,且这10个数的平方和是300,那么这组数的标准差是 .
13.(2023辽宁丹东期末)某班级在开学初进行了一次数学测试,男同学答对题目数的平均数为17,方差为11,女同学答对题目数的平均数为12,方差为16,该班男、女同学人数之比为3∶2,那么全班同学答对题目数的方差为 .
14.某学校餐厅有大米500袋,其中甲厂的大米有320袋,乙厂的大米有180袋.餐厅监管员为了得到这500袋大米的质量信息,采用分层随机抽样的方法抽取样本,并观测样本的指标值(单位:kg),计算得出甲厂样本数据的平均数为100 kg,方差为20,乙厂样本数据的平均数是100 kg,方差是30.
(1)根据以上信息,能够计算出总的样本数据的平均数和方差吗 为什么
(2)已知甲、乙两厂的样本量按比例分配,你能计算出总的样本数据的平均数和方差各为多少吗
(3)已知甲、乙两厂的样本量都是30,你能计算出总的样本数据的平均数和方差各为多少吗 将它们分别作为总体的平均数和方差的估计值合适吗 为什么
能力提升练
题组一 数据集中趋势的估计
1.(多选题)(2022广东普宁华侨中学期中)在疫情防护知识竞赛中,对某校的2 000名考生的分数进行统计,得到如图所示的频率分布直方图,其中分组的区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],60分以下视为不及格,若同一组中的数据用该组区间的中点值作代表,则下列说法中正确的是( )
A.分数在[70,80)内的考生人数最多
B.不及格的考生人数为500
C.考生分数的众数为75
D.考生分数的中位数约为75
2.(2023河南南阳月考)一段时间内没有发生大规模集体流感的标志为“连续10天,每天新增病例不超过7人”.过去10天,甲、乙、丙、丁四地新增病例数据如下,则一定符合该标志的是( )
A.甲地:平均数为3,中位数为4
B.乙地:平均数为1,方差大于0
C.丙地:中位数为2,众数为3
D.丁地:平均数为2,方差为3
3.(2022山西长治第二中学期末)四名同学各掷骰子7次,分别记录每次骰子出现的点数,根据四名同学的统计结果,可以判断出一定没有出现点数6的是( )
A.平均数为4,中位数为4
B.中位数为4,众数为3
C.平均数为3,方差为1
D.中位数为3,方差为
4.(2022四川成都期末)某学校举办了一场党史知识竞赛活动,共有500名学生参加.为了解本次知识竞赛活动的成绩,从中抽取了50名学生的分数(分数均为整数,满分为100分)进行统计,所有学生的分数都不低于60,将这50名学生的分数进行分组,第一组[60,70),第二组[70,80),第三组[80,90),第四组[90,100],得到如下频率分布直方图.
(1)求图中m的值,并估计此次知识竞赛活动学生分数的中位数;
(2)根据频率分布直方图,估计此次知识竞赛活动学生分数的平均数(同一组中的数据用该组区间的中点值作代表).若对分数不低于平均数的同学进行奖励,请估计参赛的500名学生中获奖的人数.
题组二 数据离散程度的估计
5.(2023湖北武汉月考)某校采用分层随机抽样的方法收集了高一、高二、高三年级学生的身高(单位:cm)情况,将数据整理后得到下表:
样本量 样本平均数 样本方差
高一 100 167 120
高二 100 170 150
高三 100 173 150
则总的样本方差为 .
6.(2022山东济南期末)为了调查某中学高一年级学生的身高情况,在高一年级中随机抽取100名学生测量其身高,把他们的身高(单位:cm)按照区间[160,165),[165,170),[170,175),[175,180),[180,185]分组,得到如图所示的频率分布直方图.
(1)求频率分布直方图中x的值以及样本中身高不低于175 cm的学生人数;
(2)若在统计过程中,小明与小张两名同学因事缺席,测得其余98名同学的平均身高为172 cm,方差为29,之后补测得到小明与小张的身高分别为171 cm与173 cm.试求这100个样本数据的方差.
7.为满足广大市民的日常生活所需,某快递公司以优厚的条件招聘派送员,现给出了两种日薪方案:
甲方案:底薪100元,每派送一单奖励1元;
乙方案:底薪150元,每日前55单没有奖励,超过55单的部分每单奖励10元.
(1)请分别求出这两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
(2)根据该公司所有派送员10天的派送记录,得到派送员的日均派送单数与天数如下表:
日均派送单数 50 54 56 58 60
频数(天) 2 3 2 2 1
回答下列问题:
①根据以上数据,设每名派送员的日薪为X(单位:元),试分别求出这10天中甲、乙两种方案的日薪X的平均数及方差;
②结合①中的数据,根据统计学的思想,若你去应聘派送员,选择哪种薪酬方案比较合适 并说明你的理由.
答案与分层梯度式解析
基础过关练
1.B 2.B 3.C 4.B 5.ACD 7.B 8.AB 10.B
11.BC
1.B 设9个分数从小到大排列后分别为a1,a2,a3,a4,a5,a6,a7,a8,a9,则a5为中位数,
去掉最高分a9和最低分a1后,共有7个数据,其中位数仍然是a5,故中位数一定不变.其余数字特征可能改变.故选B.
2.B 易得21名同学成绩的中位数是第11名同学的成绩,取前10名参加决赛,小明同学已经知道了自己的成绩,为了判断自己是否能进入决赛,他还需要知道第11名同学的成绩.
故选B.
3.C 对于A,4月至7月的月平均计划销售额为(万元),故A错误;
对于B,4月至7月的月平均实际销售额为(万元),故B错误;
对于C,4月至7月的月实际销售额的中位数为×(20+30)=25(万元),故C正确;
对于D,∵,∴这4个月内,总的计划销售额已经完成,故D错误.
故选C.
4.B 依题意知这组数据一共有5个数,中位数为8,则将数据从小到大排列,8是第3个数,
又唯一的众数为9,所以有两个9,其余数字均只出现一次,且这5个数中的最大数为9,
因为极差为3,所以最小的数为6,
所以这组数据为6,7,8,9,9,
所以平均数为=7.8.
故选B.
5.ACD 由题表可知,党史学习时间为8小时的人最多,为8人,故众数是8小时,A正确;
∵30×40%=12,∴第40百分位数为=8.5(小时),故B错误;
平均数为×(7×4+8×8+9×7+10×6+11×5)=9(小时),故C正确;
∵30×75%=22.5,∴上四分位数为10小时,故D正确.
故选ACD.
6.解析 (1)这30双皮鞋尺码的平均数为×(1×22+2×22.5+4×23+14×23.5+5×24+3×24.5+1×25)=23.55(cm).
共30个数据,把这30个数据按从小到大的顺序排列,中位数是第15,16个数据的平均数,为23.5,故中位数为23.5 cm.
因为23.5共出现14次,出现次数最多,
所以众数为23.5 cm.
(2)平均数、中位数对指导工厂生产没有实际意义,众数有实际意义,尺码为23.5 cm的皮鞋销量最好,工厂应多生产.
7.B 由题中频率分布直方图可知众数为65,即b=65,
平均数为45×0.15+55×0.2+65×0.25+75×0.2+85×0.1+95×0.1=67,即c=67,
因为10×(0.015+0.020)=0.35<0.5,0.35+0.025×10=0.6>0.5,所以中位数位于区间[60,70),
则有0.35+(a-60)×0.025=0.5,
解得a=66,所以b8.AB 对于A,由10×(0.015+a+0.04+0.015+0.005)=1,得a=0.025,故A正确;
对于B,平均数的估计值为35×0.15+45×0.25+55×0.4+65×0.15+75×0.05=52(kg),故B正确;
对于C,根据题中频率分布直方图可知众数的估计值为55 kg,故C错误;
对于D,因为0.15+0.25=0.4<0.5,0.15+0.25+0.4=0.8>0.5,
所以中位数位于区间[50,60),设中位数为x kg,
则0.4+(x-50)×0.04=0.5,解得x=52.5,故D错误.
故选AB.
9.解析 (1)由题中频率分布直方图,可得(0.04+0.08×2+0.12+0.16+2a+0.42+0.50)×0.5=1,解得a=0.3.
估计该市居民月均用水量不少于3吨的人数为(0.12+0.08+0.04)×0.5×60×104=72 000.
(2)由题图可估计该市居民月均用水量的众数为(2+2.5)÷2=2.25(吨).
设中位数为x吨,
因为(0.08+0.16+0.3+0.42)×0.5=0.48<0.5,0.48+0.50×0.5=0.73>0.5,所以2由0.50×(x-2)=0.5-0.48,解得x=2.04,
故估计该市居民月均用水量的中位数为2.04吨.
10.B 方差表示数据波动性的大小、稳定程度.数据越均数,方差越小,结合题图可知,B中数据主要集中在70~80内,且波动性小,故方差最小.
11.BC 对于A,由题知(x1+x2+…+xn)÷n=,而数据,…,的平均数为(+…+)÷n,不一定等于,故错误;
对于B,(2x1+2x2+…+2xn)÷n=2)2+…+(2xn-2)2]÷n=4s2,所以数据2x1,2x2,…,2xn的标准差为2s,故正确;
对于C,(x1+x2+…+xn+2n)÷n=-2)2+…+(xn+2--2)2]÷n=s2,故正确;
对于D,数据2x1-2,2x2-2,…,2xn-2的平均数为2-2,方差为[(2x1-2-2+2)2+…+(2xn-2-2+2)2]÷n=4s2,故错误.
故选BC.
规律总结 一组数据的平均数为,方差为s2,将这组数据分别加上(减去)同一个常数a,所得数据的平均数为-a),方差不变;将这组数据分别乘同一个常数b,所得数据的平均数为b,方差为b2s2.
12.答案
解析 设这10个数为xi,i=1,2,3,…,10,
则+…+(x1+x2+…+x10)=4,
所以x1+x2+…+x10=40,
则这组数的标准差是.
解后反思 方差的计算公式有两种形式,即s2=)2和s2=,可以根据题目条件灵活选择.
13.答案 19
解析 依题意,设该班男同学的人数为3a,女同学的人数为2a,a>0,
则全班同学答对题目数的平均数为=15,
所以全班同学答对题目数的方差为×[16+(12-15)2]=19.
14.解析 (1)根据题设条件可以得到总的样本数据的平均数是100 kg.不能得出总的样本数据的方差,因为不知道甲、乙两厂的大米各抽取了多少袋.
(2)能.总的样本数据的平均数为100 kg,总的样本数据的方差为×(320×20+180×30)=23.6.
(3)总的样本数据的平均数为100 kg.
总的样本数据的方差为×(20×30+30×30)=25.
甲、乙两厂样本数据的平均数都是100 kg,总的样本数据的平均数也是100 kg,所以将100 kg作为总体的平均数合适.但将25作为总体的方差不合适.因为分层随机抽样中,未按照比例抽样,总体中每个个体被抽到的可能性不完全相同,因而样本的代表性差,所以作为总体的方差的估计值不合适.
能力提升练
1.AC 2.D 3.C
1.AC 频率分布直方图中区间[70,80)对应的矩形最高,则对应的频率最大,∴分数在此区间的考生人数最多,考生分数的众数为75,故A,C正确;
分数在[40,60)内的频率为(0.005+0.015)×10=0.2,∴不及格的人数为
2 000×0.2=400,故B错误;
分数在[40,70)内的频率为(0.005+0.015+0.020)×10=0.4,设中位数为x,则0.4+(x-70)×0.030=0.5,解得x=73≈73,∴考生分数的中位数约为73,D错误.故选AC.
2.D 对于A,当甲地过去10天每天新增病例人数分别为0,0,0,2,4,4,4,4,4,8时,满足平均数为3,中位数为4,但不满足每天新增病例不超过7人,故A错误;
对于B,当乙地过去10天每天新增病例人数分别为0,0,0,0,0,0,0,0,1,9时,满足平均数为1,方差大于0,但不满足每天新增病例不超过7人,故B错误;
对于C,当丙地过去10天每天新增病例人数分别为0,0,1,1,2,2,3,3,3,8时,满足中位数为2,众数为3,但不满足每天新增病例不超过7人,故C错误;
对于D,若至少有一天新增病例超过7人,则方差大于×(8-2)2=3.6,与题意矛盾,故丁地连续10天每天新增病例不超过7人,故D正确.
故选D.
3.C 对于A,当投掷骰子出现的结果为1,2,3,4,6,6,6时,满足平均数为4,中位数为4,可以出现点数6,故A错误;
对于B,当投掷骰子出现的结果为3,3,3,4,4,5,6时,满足中位数为4,众数为3,可以出现点数6,故B错误;
对于C,若平均数为3,且出现点数6,则方差大于,又>1,与题意矛盾,故平均数为3,方差为1时,一定没有出现点数6,故C正确;
对于D,当投掷骰子出现的结果为2,2,3,3,6,6,6时,中位数为3,平均数为×(2+2+3+3+6+6+6)=4,
方差为,可以出现点数6,故D错误.
故选C.
4.解析 (1)由题中频率分布直方图知(0.01+m+0.04+0.02)×10=1,解得m=0.03.
设此次知识竞赛活动学生分数的中位数为x0,
因为数据落在[60,80)内的频率为0.4,落在[60,90)内的频率为0.8,所以80由(x0-80)×0.04=0.5-0.4,得x0=82.5,
故估计此次知识竞赛活动学生分数的中位数为82.5.
(2)由题中频率分布直方图及(1)知数据落在[60,70),[70,80),[80,90),[90,100]内的频率分别为0.1,0.3,0.4,0.2,则估计此次知识竞赛活动学生分数的平均数为65×0.1+75×0.3+85×0.4+95×0.2=82.
此次知识竞赛活动学生分数不低于82的频率为0.2+×0.4=0.52,
故估计参赛的500名学生中获奖的人数为500×0.52=260.
5.答案 146
解析 由题意知,总的样本平均数为×173=170,
∴总的样本方差为×(150+9)=146.
6.解析 (1)由题中频率分布直方图知,(0.01+0.02+x+0.06+0.07)×5=1,所以x=0.04.
易得样本中身高不低于175 cm的学生的频率为(0.04+0.02)×5=0.3,
所以样本中身高不低于175 cm的学生人数为100×0.3=30.
(2)设除小张与小明外其他98名同学的身高(单位:cm)分别为x1,x2,x3,…,x98,小张与小明的身高分别为x99,x100,这100个样本数据的平均数为,方差为s2.
由题意得(x1+x2+…+x98+x99+x100)=×(172×98+171+173)=172(cm),
又(x1-172)2+(x2-172)2+…+(x98-172)2=98×29=2 842,
所以s2==28.44.
7.解析 (1)由题意可知,甲方案日薪y与送货单数n的函数关系式为y=n×1+100=n+100,n∈N.
对于乙方案,当n≤55,n∈N时,y=150;
当n>55,n∈N时,y=150+(n-55)×10=10n-400.
故乙方案日薪y与送货单数n的函数关系式为
y=
(2)①甲方案日薪X的平均数=155(元),
方差×[2×(150-155)2+3×(154-155)2+2×(156-155)2+2×(158-155)2+(160-155)2]
=×(50+3+2+18+25)=9.8.
乙方案日薪X的平均数=163(元),
方差×[2×(150-163)2+3×(150-163)2+2×(160-163)2+2×(180-163)2+(200-163)2]
=×(338+507+18+578+1 369)=281.
②答案一:由①可知,则选择乙方案比较合适.
答案二:由①可知,,但二者相差不大,且,二者相差较大,即甲方案日薪波动情况比乙小得多,则选择甲方案比较合适.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版高中数学必修第二册同步练习题
9.2.3 总体集中趋势的估计
9.2.4 总体离散程度的估计
基础过关练
题组一 平均数、中位数、众数
1.(2023安徽九师联盟模拟)在一些比赛中,对评委打分的处理方法一般是去掉一个最高分,去掉一个最低分,然后计算余下评分的平均数作为参赛者的得分.在一次有9位评委参加的赛事中,评委对一名参赛者所打的9个分数,去掉一个最高分,去掉一个最低分后,一定不变的数字特征为( )
A.平均数 B.中位数 C.众数 D.方差
2.(2023上海实验学校月考)某学校艺术节举行弹钢琴比赛,现有21名同学报名参赛,初赛成绩各不相同,取前10名参加决赛,小明同学已经知道了自己的成绩,为了判断自己是否能进入决赛,他还需要知道21名同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
3.(2022河北保定部分学校联考)某商家2021年4月至7月的商品计划销售额和实际销售额(单位:万元)如图所示,则下列说法正确的是( )
A.4月至7月的月平均计划销售额为22万元
B.4月至7月的月平均实际销售额为27万元
C.4月至7月的月实际销售额的中位数为25万元
D.这4个月内,总的计划销售额没有完成
4.(2023山东济南模拟)某射击运动员连续射击5次,命中的环数(环数为整数)形成的一组数据中,中位数为8,唯一的众数为9,极差为3,则该组数据的平均数为( )
A.7.6 B.7.8 C.8 D.8.2
5.(多选题)(2023湖北荆门联考)某单位为了解该单位党员开展学习党史知识活动的情况,随机抽取了30名党员,对他们一周的党史学习时间进行了统计,统计数据如下表.则下列对该单位党员一周的党史学习时间的叙述正确的有( )
党史学习时间 (小时) 7 8 9 10 11
党员人数 4 8 7 6 5
A.众数是8小时
B.第40百分位数为8小时
C.平均数是9小时
D.上四分位数是10小时
6.某工厂生产并销售了30双皮鞋,其中各尺码的销售量如表所示:
皮鞋尺码 (cm) 22 22.5 23 23.5 24 24.5 25
销售量 (双) 1 2 4 14 5 3 1
(1)计算这30双皮鞋尺码的平均数、中位数、众数;
(2)从实际出发,问题(1)中的三种统计量的特征对指导工厂生产有无意义
题组二 频率分布直方图与平均数、中位数、众数
7.(2023四川成都联考)某公司为了解用户对其产品的满意度,从使用该产品的用户中随机调查了100位用户,根据用户对产品的满意度评分,得到如图所示的用户满意度评分的频率分布直方图(同一组中数据用该组区间的中点值作代表).若用户满意度评分的中位数、众数、平均数分别为a分,b分,c分,则( )
A.a
A.直方图中的a=0.025
B.过去100天香蕉的日销售量的平均数的估计值为52 kg
C.过去100天香蕉的日销售量的众数的估计值为50 kg
D.过去100天香蕉的日销售量的中位数的估计值为55 kg
9.(2022江西临川一中期末)某市共有居民60万人,为了制订合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求图中a的值,并估计该市居民月均用水量不少于3吨的人数;
(2)估计该市居民月均用水量的众数和中位数.
题组三 方差与标准差
10.以下是人数相同的四个班级某次考试成绩的频率分布直方图,其中方差最小的是( )
11.(多选题)(2022江西宜春宜丰中学、万载中学等三校期末联考)已知数据x1,x2,…,xn的平均数为,标准差为s,则( )
A.数据,…,,标准差为s2
B.数据2x1,2x2,…,2xn的平均数为2,标准差为2s
C.数据x1+2,x2+2,…,xn+2的平均数为+2,方差为s2
D.数据2x1-2,2x2-2,…,2xn-2的平均数为2-2,方差为2s2
12.(2022山东师范大学附属中学期中)现有10个数,其平均数是4,且这10个数的平方和是300,那么这组数的标准差是 .
13.(2023辽宁丹东期末)某班级在开学初进行了一次数学测试,男同学答对题目数的平均数为17,方差为11,女同学答对题目数的平均数为12,方差为16,该班男、女同学人数之比为3∶2,那么全班同学答对题目数的方差为 .
14.某学校餐厅有大米500袋,其中甲厂的大米有320袋,乙厂的大米有180袋.餐厅监管员为了得到这500袋大米的质量信息,采用分层随机抽样的方法抽取样本,并观测样本的指标值(单位:kg),计算得出甲厂样本数据的平均数为100 kg,方差为20,乙厂样本数据的平均数是100 kg,方差是30.
(1)根据以上信息,能够计算出总的样本数据的平均数和方差吗 为什么
(2)已知甲、乙两厂的样本量按比例分配,你能计算出总的样本数据的平均数和方差各为多少吗
(3)已知甲、乙两厂的样本量都是30,你能计算出总的样本数据的平均数和方差各为多少吗 将它们分别作为总体的平均数和方差的估计值合适吗 为什么
能力提升练
题组一 数据集中趋势的估计
1.(多选题)(2022广东普宁华侨中学期中)在疫情防护知识竞赛中,对某校的2 000名考生的分数进行统计,得到如图所示的频率分布直方图,其中分组的区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],60分以下视为不及格,若同一组中的数据用该组区间的中点值作代表,则下列说法中正确的是( )
A.分数在[70,80)内的考生人数最多
B.不及格的考生人数为500
C.考生分数的众数为75
D.考生分数的中位数约为75
2.(2023河南南阳月考)一段时间内没有发生大规模集体流感的标志为“连续10天,每天新增病例不超过7人”.过去10天,甲、乙、丙、丁四地新增病例数据如下,则一定符合该标志的是( )
A.甲地:平均数为3,中位数为4
B.乙地:平均数为1,方差大于0
C.丙地:中位数为2,众数为3
D.丁地:平均数为2,方差为3
3.(2022山西长治第二中学期末)四名同学各掷骰子7次,分别记录每次骰子出现的点数,根据四名同学的统计结果,可以判断出一定没有出现点数6的是( )
A.平均数为4,中位数为4
B.中位数为4,众数为3
C.平均数为3,方差为1
D.中位数为3,方差为
4.(2022四川成都期末)某学校举办了一场党史知识竞赛活动,共有500名学生参加.为了解本次知识竞赛活动的成绩,从中抽取了50名学生的分数(分数均为整数,满分为100分)进行统计,所有学生的分数都不低于60,将这50名学生的分数进行分组,第一组[60,70),第二组[70,80),第三组[80,90),第四组[90,100],得到如下频率分布直方图.
(1)求图中m的值,并估计此次知识竞赛活动学生分数的中位数;
(2)根据频率分布直方图,估计此次知识竞赛活动学生分数的平均数(同一组中的数据用该组区间的中点值作代表).若对分数不低于平均数的同学进行奖励,请估计参赛的500名学生中获奖的人数.
题组二 数据离散程度的估计
5.(2023湖北武汉月考)某校采用分层随机抽样的方法收集了高一、高二、高三年级学生的身高(单位:cm)情况,将数据整理后得到下表:
样本量 样本平均数 样本方差
高一 100 167 120
高二 100 170 150
高三 100 173 150
则总的样本方差为 .
6.(2022山东济南期末)为了调查某中学高一年级学生的身高情况,在高一年级中随机抽取100名学生测量其身高,把他们的身高(单位:cm)按照区间[160,165),[165,170),[170,175),[175,180),[180,185]分组,得到如图所示的频率分布直方图.
(1)求频率分布直方图中x的值以及样本中身高不低于175 cm的学生人数;
(2)若在统计过程中,小明与小张两名同学因事缺席,测得其余98名同学的平均身高为172 cm,方差为29,之后补测得到小明与小张的身高分别为171 cm与173 cm.试求这100个样本数据的方差.
7.为满足广大市民的日常生活所需,某快递公司以优厚的条件招聘派送员,现给出了两种日薪方案:
甲方案:底薪100元,每派送一单奖励1元;
乙方案:底薪150元,每日前55单没有奖励,超过55单的部分每单奖励10元.
(1)请分别求出这两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
(2)根据该公司所有派送员10天的派送记录,得到派送员的日均派送单数与天数如下表:
日均派送单数 50 54 56 58 60
频数(天) 2 3 2 2 1
回答下列问题:
①根据以上数据,设每名派送员的日薪为X(单位:元),试分别求出这10天中甲、乙两种方案的日薪X的平均数及方差;
②结合①中的数据,根据统计学的思想,若你去应聘派送员,选择哪种薪酬方案比较合适 并说明你的理由.
答案与分层梯度式解析
基础过关练
1.B 2.B 3.C 4.B 5.ACD 7.B 8.AB 10.B
11.BC
1.B 设9个分数从小到大排列后分别为a1,a2,a3,a4,a5,a6,a7,a8,a9,则a5为中位数,
去掉最高分a9和最低分a1后,共有7个数据,其中位数仍然是a5,故中位数一定不变.其余数字特征可能改变.故选B.
2.B 易得21名同学成绩的中位数是第11名同学的成绩,取前10名参加决赛,小明同学已经知道了自己的成绩,为了判断自己是否能进入决赛,他还需要知道第11名同学的成绩.
故选B.
3.C 对于A,4月至7月的月平均计划销售额为(万元),故A错误;
对于B,4月至7月的月平均实际销售额为(万元),故B错误;
对于C,4月至7月的月实际销售额的中位数为×(20+30)=25(万元),故C正确;
对于D,∵,∴这4个月内,总的计划销售额已经完成,故D错误.
故选C.
4.B 依题意知这组数据一共有5个数,中位数为8,则将数据从小到大排列,8是第3个数,
又唯一的众数为9,所以有两个9,其余数字均只出现一次,且这5个数中的最大数为9,
因为极差为3,所以最小的数为6,
所以这组数据为6,7,8,9,9,
所以平均数为=7.8.
故选B.
5.ACD 由题表可知,党史学习时间为8小时的人最多,为8人,故众数是8小时,A正确;
∵30×40%=12,∴第40百分位数为=8.5(小时),故B错误;
平均数为×(7×4+8×8+9×7+10×6+11×5)=9(小时),故C正确;
∵30×75%=22.5,∴上四分位数为10小时,故D正确.
故选ACD.
6.解析 (1)这30双皮鞋尺码的平均数为×(1×22+2×22.5+4×23+14×23.5+5×24+3×24.5+1×25)=23.55(cm).
共30个数据,把这30个数据按从小到大的顺序排列,中位数是第15,16个数据的平均数,为23.5,故中位数为23.5 cm.
因为23.5共出现14次,出现次数最多,
所以众数为23.5 cm.
(2)平均数、中位数对指导工厂生产没有实际意义,众数有实际意义,尺码为23.5 cm的皮鞋销量最好,工厂应多生产.
7.B 由题中频率分布直方图可知众数为65,即b=65,
平均数为45×0.15+55×0.2+65×0.25+75×0.2+85×0.1+95×0.1=67,即c=67,
因为10×(0.015+0.020)=0.35<0.5,0.35+0.025×10=0.6>0.5,所以中位数位于区间[60,70),
则有0.35+(a-60)×0.025=0.5,
解得a=66,所以b
对于B,平均数的估计值为35×0.15+45×0.25+55×0.4+65×0.15+75×0.05=52(kg),故B正确;
对于C,根据题中频率分布直方图可知众数的估计值为55 kg,故C错误;
对于D,因为0.15+0.25=0.4<0.5,0.15+0.25+0.4=0.8>0.5,
所以中位数位于区间[50,60),设中位数为x kg,
则0.4+(x-50)×0.04=0.5,解得x=52.5,故D错误.
故选AB.
9.解析 (1)由题中频率分布直方图,可得(0.04+0.08×2+0.12+0.16+2a+0.42+0.50)×0.5=1,解得a=0.3.
估计该市居民月均用水量不少于3吨的人数为(0.12+0.08+0.04)×0.5×60×104=72 000.
(2)由题图可估计该市居民月均用水量的众数为(2+2.5)÷2=2.25(吨).
设中位数为x吨,
因为(0.08+0.16+0.3+0.42)×0.5=0.48<0.5,0.48+0.50×0.5=0.73>0.5,所以2
故估计该市居民月均用水量的中位数为2.04吨.
10.B 方差表示数据波动性的大小、稳定程度.数据越均数,方差越小,结合题图可知,B中数据主要集中在70~80内,且波动性小,故方差最小.
11.BC 对于A,由题知(x1+x2+…+xn)÷n=,而数据,…,的平均数为(+…+)÷n,不一定等于,故错误;
对于B,(2x1+2x2+…+2xn)÷n=2)2+…+(2xn-2)2]÷n=4s2,所以数据2x1,2x2,…,2xn的标准差为2s,故正确;
对于C,(x1+x2+…+xn+2n)÷n=-2)2+…+(xn+2--2)2]÷n=s2,故正确;
对于D,数据2x1-2,2x2-2,…,2xn-2的平均数为2-2,方差为[(2x1-2-2+2)2+…+(2xn-2-2+2)2]÷n=4s2,故错误.
故选BC.
规律总结 一组数据的平均数为,方差为s2,将这组数据分别加上(减去)同一个常数a,所得数据的平均数为-a),方差不变;将这组数据分别乘同一个常数b,所得数据的平均数为b,方差为b2s2.
12.答案
解析 设这10个数为xi,i=1,2,3,…,10,
则+…+(x1+x2+…+x10)=4,
所以x1+x2+…+x10=40,
则这组数的标准差是.
解后反思 方差的计算公式有两种形式,即s2=)2和s2=,可以根据题目条件灵活选择.
13.答案 19
解析 依题意,设该班男同学的人数为3a,女同学的人数为2a,a>0,
则全班同学答对题目数的平均数为=15,
所以全班同学答对题目数的方差为×[16+(12-15)2]=19.
14.解析 (1)根据题设条件可以得到总的样本数据的平均数是100 kg.不能得出总的样本数据的方差,因为不知道甲、乙两厂的大米各抽取了多少袋.
(2)能.总的样本数据的平均数为100 kg,总的样本数据的方差为×(320×20+180×30)=23.6.
(3)总的样本数据的平均数为100 kg.
总的样本数据的方差为×(20×30+30×30)=25.
甲、乙两厂样本数据的平均数都是100 kg,总的样本数据的平均数也是100 kg,所以将100 kg作为总体的平均数合适.但将25作为总体的方差不合适.因为分层随机抽样中,未按照比例抽样,总体中每个个体被抽到的可能性不完全相同,因而样本的代表性差,所以作为总体的方差的估计值不合适.
能力提升练
1.AC 2.D 3.C
1.AC 频率分布直方图中区间[70,80)对应的矩形最高,则对应的频率最大,∴分数在此区间的考生人数最多,考生分数的众数为75,故A,C正确;
分数在[40,60)内的频率为(0.005+0.015)×10=0.2,∴不及格的人数为
2 000×0.2=400,故B错误;
分数在[40,70)内的频率为(0.005+0.015+0.020)×10=0.4,设中位数为x,则0.4+(x-70)×0.030=0.5,解得x=73≈73,∴考生分数的中位数约为73,D错误.故选AC.
2.D 对于A,当甲地过去10天每天新增病例人数分别为0,0,0,2,4,4,4,4,4,8时,满足平均数为3,中位数为4,但不满足每天新增病例不超过7人,故A错误;
对于B,当乙地过去10天每天新增病例人数分别为0,0,0,0,0,0,0,0,1,9时,满足平均数为1,方差大于0,但不满足每天新增病例不超过7人,故B错误;
对于C,当丙地过去10天每天新增病例人数分别为0,0,1,1,2,2,3,3,3,8时,满足中位数为2,众数为3,但不满足每天新增病例不超过7人,故C错误;
对于D,若至少有一天新增病例超过7人,则方差大于×(8-2)2=3.6,与题意矛盾,故丁地连续10天每天新增病例不超过7人,故D正确.
故选D.
3.C 对于A,当投掷骰子出现的结果为1,2,3,4,6,6,6时,满足平均数为4,中位数为4,可以出现点数6,故A错误;
对于B,当投掷骰子出现的结果为3,3,3,4,4,5,6时,满足中位数为4,众数为3,可以出现点数6,故B错误;
对于C,若平均数为3,且出现点数6,则方差大于,又>1,与题意矛盾,故平均数为3,方差为1时,一定没有出现点数6,故C正确;
对于D,当投掷骰子出现的结果为2,2,3,3,6,6,6时,中位数为3,平均数为×(2+2+3+3+6+6+6)=4,
方差为,可以出现点数6,故D错误.
故选C.
4.解析 (1)由题中频率分布直方图知(0.01+m+0.04+0.02)×10=1,解得m=0.03.
设此次知识竞赛活动学生分数的中位数为x0,
因为数据落在[60,80)内的频率为0.4,落在[60,90)内的频率为0.8,所以80
故估计此次知识竞赛活动学生分数的中位数为82.5.
(2)由题中频率分布直方图及(1)知数据落在[60,70),[70,80),[80,90),[90,100]内的频率分别为0.1,0.3,0.4,0.2,则估计此次知识竞赛活动学生分数的平均数为65×0.1+75×0.3+85×0.4+95×0.2=82.
此次知识竞赛活动学生分数不低于82的频率为0.2+×0.4=0.52,
故估计参赛的500名学生中获奖的人数为500×0.52=260.
5.答案 146
解析 由题意知,总的样本平均数为×173=170,
∴总的样本方差为×(150+9)=146.
6.解析 (1)由题中频率分布直方图知,(0.01+0.02+x+0.06+0.07)×5=1,所以x=0.04.
易得样本中身高不低于175 cm的学生的频率为(0.04+0.02)×5=0.3,
所以样本中身高不低于175 cm的学生人数为100×0.3=30.
(2)设除小张与小明外其他98名同学的身高(单位:cm)分别为x1,x2,x3,…,x98,小张与小明的身高分别为x99,x100,这100个样本数据的平均数为,方差为s2.
由题意得(x1+x2+…+x98+x99+x100)=×(172×98+171+173)=172(cm),
又(x1-172)2+(x2-172)2+…+(x98-172)2=98×29=2 842,
所以s2==28.44.
7.解析 (1)由题意可知,甲方案日薪y与送货单数n的函数关系式为y=n×1+100=n+100,n∈N.
对于乙方案,当n≤55,n∈N时,y=150;
当n>55,n∈N时,y=150+(n-55)×10=10n-400.
故乙方案日薪y与送货单数n的函数关系式为
y=
(2)①甲方案日薪X的平均数=155(元),
方差×[2×(150-155)2+3×(154-155)2+2×(156-155)2+2×(158-155)2+(160-155)2]
=×(50+3+2+18+25)=9.8.
乙方案日薪X的平均数=163(元),
方差×[2×(150-163)2+3×(150-163)2+2×(160-163)2+2×(180-163)2+(200-163)2]
=×(338+507+18+578+1 369)=281.
②答案一:由①可知,则选择乙方案比较合适.
答案二:由①可知,,但二者相差不大,且,二者相差较大,即甲方案日薪波动情况比乙小得多,则选择甲方案比较合适.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
