2024人教版高中数学必修第二册同步练习题--第九章 统计拔高练(含解析)
文档属性
| 名称 | 2024人教版高中数学必修第二册同步练习题--第九章 统计拔高练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024人教版高中数学必修第二册同步练习题
综合拔高练
五年高考练
考点1 统计图表的应用
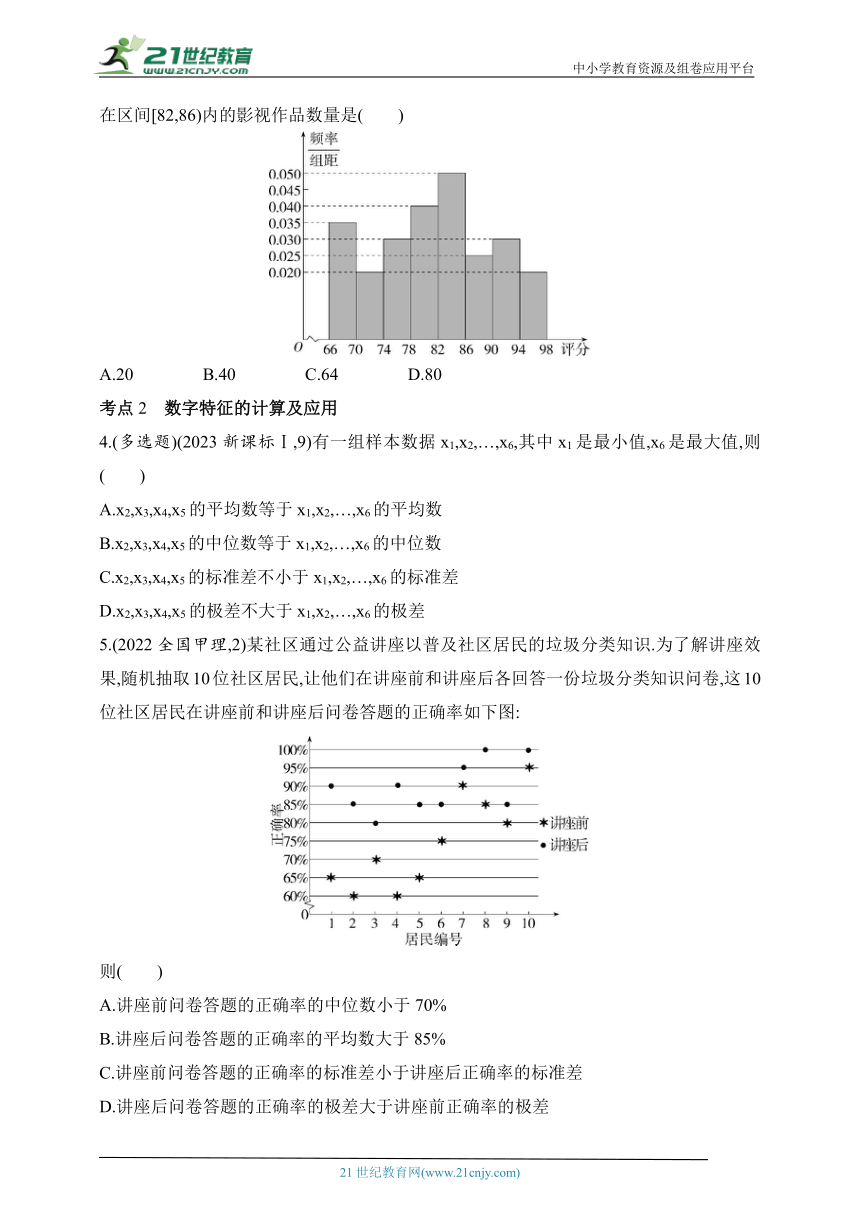
1.(2021全国甲理,2)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是 ( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
2.(多选题)(2020新高考Ⅱ,9)我国新冠肺炎疫情防控进入常态化,各地有序推动复工复产,下面是某地连续11天的复工、复产指数折线图.
根据该折线图,( )
A.这11天复工指数和复产指数均逐日增加
B.在这11天期间,复产指数的增量大于复工指数的增量
C.第3天至第11天,复工指数和复产指数都超过80%
D.第9天至第11天,复产指数的增量大于复工指数的增量
3.(2021天津,4)从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8组:[66,70),[70,74),…,[94,98],并整理得到如下的频率分布直方图,则评分在区间[82,86)内的影视作品数量是( )
A.20 B.40 C.64 D.80
考点2 数字特征的计算及应用
4.(多选题)(2023新课标Ⅰ,9)有一组样本数据x1,x2,…,x6,其中x1是最小值,x6是最大值,则( )
A.x2,x3,x4,x5的平均数等于x1,x2,…,x6的平均数
B.x2,x3,x4,x5的中位数等于x1,x2,…,x6的中位数
C.x2,x3,x4,x5的标准差不小于x1,x2,…,x6的标准差
D.x2,x3,x4,x5的极差不大于x1,x2,…,x6的极差
5.(2022全国甲理,2)某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如下图:
则( )
A.讲座前问卷答题的正确率的中位数小于70%
B.讲座后问卷答题的正确率的平均数大于85%
C.讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D.讲座后问卷答题的正确率的极差大于讲座前正确率的极差
6.(多选题)(2021新高考Ⅱ,9)下列统计量中可用于度量样本x1,x2,…,xn离散程度的有( )
A.x1,x2,…,xn的标准差
B.x1,x2,…,xn的中位数
C.x1,x2,…,xn的极差
D.x1,x2,…,xn的平均数
7.(2020全国Ⅲ文,3)设一组样本数据x1,x2,…,xn的方差为0.01,则数据10x1,10x2,…,10xn的方差为( )
A.0.01 B.0.1 C.1 D.10
8.(多选题)(2021新高考Ⅰ,9)有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据y1,y2,…,yn,其中yi=xi+c(i=1,2,…,n),c为非零常数,则( )
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同
D.两组样本数据的样本极差相同
9.(2020全国Ⅲ理,3)在一组样本数据中,1,2,3,4出现的频率分别为p1,p2,p3,p4,且则下面四种情形中,对应样本的标准差最大的一组是( )
A.p1=p4=0.1,p2=p3=0.4
B.p1=p4=0.4,p2=p3=0.1
C.p1=p4=0.2,p2=p3=0.3
D.p1=p4=0.3,p2=p3=0.2
10.(2023全国乙理,17)某厂为比较甲、乙两种工艺对橡胶产品伸缩率的处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后的橡胶产品的伸缩率.甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为xi,yi(i=1,2,…,10),试验结果如下:
试验 序号i 1 2 3 4 5 6 7 8 9 10
伸缩 率xi 545 533 551 522 575 544 541 568 596 548
伸缩 率yi 536 527 543 530 560 533 522 550 576 536
记zi=xi-yi(i=1,2,…,10),记z1,z2,…,z10的样本平均数为,样本方差为s2.
(1)求,s2;
(2)判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高如果≥2,则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高,否则不认为有显著提高.
11.(2021全国乙理,17)某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备 9.8 10.3 10.0 10.2 9.9
新设备 10.1 10.4 10.1 10.0 10.1
旧设备 9.8 10.0 10.1 10.2 9.7
新设备 10.3 10.6 10.5 10.4 10.5
旧设备和新设备生产产品的该项指标的样本平均数分别记为 ,样本方差分别记为.
(1)求;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高如果≥2,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高.
三年模拟练
应用实践
1.(2023山东泰安模拟)少年强则国强,少年智则国智.党和政府一直重视青少年的健康成长,出台了一系列政策和行动计划,旨在提高学生身体素质.为了加强对学生的营养健康监测,某校在3 000名学生中,抽查了100名学生的体重数据,根据所得数据绘制了样本的频率分布直方图如图所示,则下列结论正确的是(同一组中数据用该组区间中点值作代表)( )
A.样本的众数为65 kg
B.样本的第80百分位数为72.5 kg
C.样本的平均数为67.5 kg
D.该校学生中体重低于65 kg的大约有1 000人
2.(2023浙江绍兴模拟)已知一组样本数据共有9个数,其平均数为8,方差为12.将这组样本数据增加一个数据后,所得新的样本数据的平均数为9,则新的样本数据的方差为( )
A.18.2 B.19.6
C.19.8 D.21.4
3.(2023山东济南实验中学模拟)在高三某次模拟考试中,甲、乙两个班级的数学成绩统计如下表:
班级 人数 平均分 方差
甲 40 70 5
乙 60 80 8
则两个班所有学生的数学成绩的方差为( )
A.6.5 B.13
C.30.8 D.31.8
4.(多选题)(2022山西运城月考)第一组样本数据:x1,x2,…,xn,由这组数据得到第二组样本数据:y1,y2,…,yn,其中yi=axi+b(i=1,2,…,n),a,b为正数,则下列命题正确的是( )
A.当a=1时,两组样本数据的平均数不相同
B.第二组样本数据的极差是第一组的a倍
C.第二组样本数据的标准差是第一组的a倍
D.第二组样本数据的方差是第一组的a倍
5.(多选题)(2023广东潮州模拟)根据气象学上的标准,如果连续5天的日平均气温都低于10 ℃即为入冬.现将连续5天的日平均气温(单位:℃)的记录数据(记录数据都是自然数)作为一组样本,则下列样本中一定符合入冬指标的有( )
A.平均数小于4
B.平均数小于4且极差小于或等于3
C.平均数小于4且标准差小于或等于4
D.众数等于5且极差小于或等于4
6.(多选题)(2022湖南长沙期末)某市2022年经过招商引资后,经济收入较前一年增加了一倍,实现翻番,为更好地了解该市的经济收入变化情况,统计了该市招商引资前后的年经济收入构成比例,得到如下扇形图:
则下列结论中正确的是( )
A.招商引资后,工资净收入较前一年增加
B.招商引资后,转移净收入是前一年的1.25倍
C.招商引资后,转移净收入与财产净收入的总和超过了该年经济收入的
D.招商引资后,经营净收入较前一年增加了一倍
7.(2022安徽淮南模拟)近年来,我国肥胖人群的规模急速增长,肥胖人群有很大的心血管安全隐患.目前,国际上常用身体质量指数(BMI)来衡量人体胖瘦程度以及是否健康,其计算公式是BMI=.我国成人的BMI数值标准为:BMI<18.5为偏瘦,18.5≤BMI<24为正常,24≤BMI<28为偏胖,BMI≥28为肥胖.为了解某公司员工的身体肥胖情况,研究人员从公司员工体检数据中,利用分层随机抽样得到15名员工的BMI数据如下:23.5,21.6,30.6,22.1,23.7,20.6,25.5,23.9,20.8,21.5,21.8,18.2,25.2,21.5,19.1.则该组数据的第70百分位数为 .
8.(2023辽宁沈阳期末)为了解某企业员工对党史的学习情况,对该企业员工进行问卷调查,已知他们的得分都处在A,B,C,D四个区间内,根据调查结果得到下面的统计图.已知该企业男员工占,则下列结论中,正确结论的个数是 .
①男、女员工得分在A区间的占比相同;
②在各得分区间内,男员工的人数都多于女员工的人数;
③得分在C区间的员工最多;
④得分在D区间的员工占总人数的20%.
9.(2023江西五市九校协作体联考)江西省作为全国第四批启动高考综合改革的七个省份之一,从2021年秋季学期起启动实施高考综合改革,实行高考科目“3+1+2”模式.“3”指语文、数学、外语三门统考学科,以原始分计入高考成绩;“1”指考生从物理、历史两门学科中“首选”一门学科,以原始分计入高考成绩;“2”指考生从政治、地理、化学、生物四门学科中“再选”两门学科,以等级分计入高考成绩.按照方案,“再选”学科的等级分赋分规则如下:将考生原始成绩从高到低划分为A,B,C,D,E五个等级,各等级人数所占比例及赋分区间如表,
等级 A B C D E
人数 比例 15% 35% 35% 13% 2%
赋分 区间 [86,100] [71,85] [56,70] [41,55] [30,40]
将各等级内考生的原始分依照等比例转换法分别转换到赋分区间内,得到等级分,转换公式为,其中Y1,Y2分别表示原始分区间的最低分和最高分,T1,T2分别表示等级赋分区间的最低分和最高分,Y表示考生的原始分,T表示考生的等级分,规定原始分为Y1时,等级分为T1,计算结果四舍五入取整.某次化学考试的考生原始分最低分为50,最高分为98,呈连续整数分布,其频率分布直方图如下:
(1)同一组数据以该组区间的中点值作代表,求实数a的值并估计本次考试的平均分;
(2)按照等级分赋分规则,估计此次化学考试成绩中A等级的原始分区间;
(3)用估计的结果近似代替原始分区间,若某学生化学成绩的原始分为90分,试计算其等级分.
10.(2022山西朔州怀仁一中二模)某经销商采购了一批水果,根据某些评价指标进行打分,现从中随机抽取20筐(每筐1 kg),其分数如下:17,23,27,31,36,40,45,50,51,51,58,63,65,68,71,78,79,80,85,95.根据以往的数据认定分数在区间[0,25],(25,50],(50,75],(75,100]内的分别对应四级、三级、二级、一级.
(1)试求这20筐水果分数的平均数;
(2)经销商参考以下两种销售方案对这批水果进行销售:
方案一:按这批水果分数的平均数对应的等级出售;
方案二:按这批水果分数对应的等级出售.
不同等级水果的售价如表所示:
等级 一级 二级 三级 四级
售价 (万元/吨) 2 1.8 1.5 1.2
请从经销商的角度,根据售价分析采用哪种销售方案较好,并说明理由.
11.(2022福建福州期末)某市为了了解人们对“中国梦”的伟大构想的认知程度,针对本市不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(95分及以上为认知程度高),结果认知程度高的有m人,按年龄(单位:岁)分成5组,其中第一组:[20,25),第二组:[25,30),第三组:[30,35),第四组:[35,40),第五组:[40,45],得到如图所示的频率分布直方图.
(1)根据频率分布直方图,估计这些人年龄的平均数和第80百分位数;
(2)现从以上各组中用分层随机抽样的方法抽取20人,担任本市的“中国梦”宣传使者.若第四组宣传使者的年龄的平均数与方差分别为37岁和,第五组宣传使者的年龄的平均数与方差分别为43岁和1,求这20人中年龄在[35,45]内的所有人的年龄的方差.
答案与分层梯度式解析
综合拔高练
五年高考练
1.C 2.CD 3.D 4.BD 5.B 6.AC 7.C 8.CD
9.B
1.C 由题中频率分布直方图可得,该地农户家庭年收入低于4.5万元和不低于10.5万元的频率分别为0.06和0.1,则农户比率分别为6%和10%,故A,B中结论正确;家庭年收入介于4.5万元和8.5万元之间的频率为0.1+0.14+0.2+0.2=0.64,故D中结论正确;家庭年收入的平均值为0.02×3+0.04×4+0.1×5+0.14×6+0.2×7+0.2×8+0.1×9+0.1×10+0.04×11+
0.02×12+0.02×13+0.02×14=7.68(万元),因为7.68>6.5,所以估计该地农户家庭年收入的平均值超过6.5万元,故C中结论不正确.故选C.
2.CD 由题中折线图可知,第7天至第9天,复产指数与复工指数均减少,故选项A错误.在这11天期间,复产指数的增量小于复工指数的增量,故选项B错误.易知C,D正确.故选CD.
3.D 根据题意得,评分在区间[82,86)内的影视作品数量是400×0.05×4=80.故选D.
4.BD 对于A,如1,2,2,2,2,4的平均数不等于2,2,2,2的平均数,故A错误;
对于B,不妨设x2≤x3≤x4≤x5,x2,x3,x4,x5的中位数为,x1,x2,…,x6的中位数为,故B正确;
对于C,x1,x2,…,x6的数据波动性更大,故C错误;
对于D,不妨设x2≤x3≤x4≤x5,则x1≤x2≤x3≤x4≤x5≤x6,所以x5-x2≤x6-x1,故D正确.
故选BD.
5.B 对于A,将讲座前的10个数据从小到大排列依次为60%,60%,65%,65%,70%,75%,80%,85%,90%,95%,易知这10个数据的中位数是第5个与第6个数据的平均数,为=72.5%>70%,故A错误;
对于B,×(90%+85%+80%+90%+85%+85%+95%+100%+85%+100%)=89.5%>85%,故B正确;
对于C,由题图可知,讲座前的数据与讲座后的数据相比,较分散,因此标准差较大,故C错误;
对于D,讲座前问卷答题的正确率的极差为95%-60%=35%,讲座后问卷答题的正确率的极差为100%-80%=20%,20%<35%,故D错误.故选B.
6.AC 由标准差的定义可知,标准差考查的是数据的离散程度;
由中位数的定义可知,中位数考查的是数据的集中趋势;
由极差的定义可知,极差考查的是数据的离散程度;
由平均数的定义可知,平均数考查的是数据的集中趋势.
故选AC.
7.C 根据方差的性质,可得数据10x1,10x2,…,10xn的方差为100×0.01=1,故选C.
8.CD A项,设xi,则xi+c,所以+c,因为c≠0,所以,所以A选项错误.
B项,因为yi=xi+c(i=1,2,…,n),所以y1,y2,…,yn的中位数是x1,x2,…,xn的中位数加c,所以B选项错误.
C项,设)2,
则)2,
所以,所以两组数据的方差相同,从而这两组数据的标准差相同,所以C选项正确.
D项,不妨设x1≤x2≤…≤xn,则第一组数据的极差为xn-x1,另设y1≤y2≤…≤yn,则第二组数据的极差为yn-y1=(xn+c)-(x1+c)=xn-x1,所以两组数据的极差相同,所以D选项正确.故选CD.
9.B 根据平均数方差s2=(xi-)2pi以及方差与标准差的关系,得各选项对应样本的标准差如下表.
选项 平均数 方差s2 标准差s
A 2.5 0.65
B 2.5 1.85
C 2.5 1.05
D 2.5 1.45
由此可知选项B对应样本的标准差最大,故选B.
10.解析 (1)zi=xi-yi(i=1,2,…,10)的值依次为9,6,8,-8,15,11,19,18,20,12,则×(9+6+8-8+15+11+19+18+20+12)=11,
s2=×[(9-11)2+(6-11)2+(8-11)2+(-8-11)2+(15-11)2+(11-11)2+(19-11)2+(18-11)2+(20-11)2+(12-11)2]=61.
(2)由(1)知=11,s2=61,则>0,∴,即甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高.
11.解析 (1)×(9.8+10.3+10.0+10.2+9.9+9.8+10.0+10.1+10.2+9.7)=10.0.
×(10.1+10.4+10.1+10.0+10.1+10.3+10.6+10.5+10.4+10.5)=10.3.
×[(9.8-10.0)2+(10.3-10.0)2+(10.0-10.0)2+(10.2-10.0)2+(9.9-10.0)2+(9.8-10.0)2+(10.0-10.0)2+(10.1-10.0)2+(10.2-10.0)2+(9.7-10.0)2]=0.036.
×[(10.1-10.3)2+(10.4-10.3)2+(10.1-10.3)2+(10.0-10.3)2+(10.1-10.3)2+(10.3-10.3)2+(10.6-10.3)2+(10.5-10.3)2+(10.4-10.3)2+(10.5-10.3)2]=0.04.
(2)由(1)得=0.076,
从而()=0.030 4,所以(,又,故,因此新设备生产产品的该项指标的均值较旧设备有显著提高.
三年模拟练
1.B 2.C 3.C 4.ABC 5.BD 6.AD
1.B 由题中频率分布直方图可得样本的众数为67.5 kg,A错误;
平均数为57.5×0.15+62.5×0.25+67.5×0.3+72.5×0.2+77.5×0.1=66.75(kg),C错误;
因为体重位于[55,60),[60,65),[65,70),[70,75)的频率分别为0.15,0.25,0.3,0.2,0.15+0.25+0.3=0.7<0.8,0.15+0.25+0.3+0.2=0.9>0.8,
所以第80百分位数位于区间[70,75),设第80百分位数为x kg,
则0.7+(x-70)×0.04=0.8,解得x=72.5,
即样本的第80百分位数为72.5 kg,B正确;
样本中低于65 kg的学生的频率为0.15+0.25=0.4,
所以该校学生中体重低于65 kg的大约有3 000×0.4=1 200(人),D错误.
故选B.
2.C 设增加的数为k,原来的9个数分别为a1,a2,…,a9,
则a1+a2+…+a9=72,a1+a2+…+a9+k=90,
所以k=18,
又因为(ai-8)2=12,即(ai-8)2=108,
所以(ai-8)+9+81]=19.8.故选C.
3.C 因为甲班的平均分=70,乙班的平均分=80,
所以两个班所有学生的平均分=76,
所以两个班所有学生的数学成绩的方差s2=×[8+(80-76)2]=30.8.故选C.
4.ABC 设第一组样本数据x1,x2,…,xn的平均数为,方差为s2,
则第二组样本数据ax1+b,ax2+b,…,axn+b的平均数为a+b,方差为a2s2.
对于A选项,当a=1时,第二组样本数据的平均数为+b,因为b>0,所以+b≠,故A正确;
对于B选项,由极差的定义知,若第一组的极差为xmax-xmin,则第二组的极差为ymax-ymin=a(xmax+b)-a(xmin+b)=a(xmax-xmin),即第二组样本数据的极差是第一组的a倍,故B正确;
对于C,D选项,根据方差的性质得,第二组样本数据的方差是第一组的a2倍,则第二组样本数据的标准差是第一组的a倍,故C正确,D错误.
故选ABC.
5.BD 对于A,举反例:0,0,0,0,15,平均数为3,但不符合入冬指标,A错误;
对于B,假设有数据大于或等于10,则由极差小于或等于3知,此组数据中最小的数大于或等于7,与平均数小于4矛盾,故假设不成立,B正确;
对于C,举反例:1,1,1,1,11,平均数为3,且标准差为4,但不符合入冬指标,C错误;
对于D,众数等于5且极差小于或等于4时,最大的数不超过9,D正确.
故选BD.
6.AD 设招商引资前年经济收入为M,则招商引资后年经济收入为2M.
对于A,招商引资前工资净收入为M×60%=0.6M,而招商引资后工资净收入为2M×37%=0.74M,所以工资净收入增加了,故A正确;
对于B,招商引资前转移净收入为M×4%=0.04M,招商引资后转移净收入为2M×5%=0.1M,所以招商引资后,转移净收入是前一年的2.5倍,故B错误;
对于C,招商引资后,转移净收入与财产净收入的总和为0.1M+0.56M=0.66M<×2M=0.8M,所以招商引资后,转移净收入与财产净收入的总和低于该年经济收入的,故C错误;
对于D,招商引资前经营净收入为M×30%=0.3M,招商引资后经营净收入为2M×30%=0.6M,所以招商引资后,经营净收入较前一年增加了一倍,故D正确.
故选AD.
7.答案 23.7
解析 15名员工的BMI数据由小到大排列为18.2,19.1,20.6,20.8,21.5,21.5,21.6,21.8,22.1,23.5,23.7,23.9,25.2,25.5,30.6,
由15×70%=10.5,得该组数据的第70百分位数是第11个数,即23.7.
8.答案 1
解析 设员工总人数为n,
由题中条形图可得女员工人数为20+60+70+50=200,
所以,解得n=500,
所以男员工人数为500-200=300.
对于①,女员工得分在A区间的占比为=10%,男员工得分在A区间的占比为1-40%-35%-15%=10%,故①正确;
对于②,女员工得分在A区间的有20人,B区间的有60人,C区间的有70人,D区间的有50人,
男员工得分在A区间的有300×10%=30(人),B区间的有300×40%=120(人),C区间的有300×35%=105(人),D区间的有300×15%=45(人),
所以D区间男员工的人数少于女员工,故②错误;
对于③,得分在B区间的员工有60+120=180(人),C区间的有70+105=175(人),所以B区间人数比C区间多,故③错误;
对于④,得分在D区间的有50+45=95(人),所以得分在D区间的员工占总人数的×100%=19%,故④错误.
综上,正确结论的个数是1.
9.解析 (1)由题中频率分布直方图可知,(2a+0.04+0.03+0.02)×10=1,解得a=0.005.
估计本次考试的平均分为55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73(分).
(2)A等级所占的人数比例为15%,由题中频率分布直方图知,原始分位于区间[90,100]的占比为5%,位于区间[80,90)的占比为20%,所以最低原始分在[80,90)内,设最低原始分为x,则(90-x)×0.02=15%-5%,解得x=85,所以估计此次化学考试成绩中A等级的原始分区间为[85,98].
(3)由(2)知,化学成绩的原始分为90分是A等级,则T1=86,T2=100,Y1=85,Y2=98,Y=90,代入公式,得,解得T=≈91,故该学生的等级分为91分.
10.解析 (1)这20筐水果分数的平均数为×(17+23+27+31+36+40+45+50+51+51+58+63+65+68+71+78+79+80+85+95)=55.65.
(2)采用方案一较好.理由如下:
对于方案一,由于分数的平均数为55.65,对应二级,所以可以估计这批水果的售价为1.8万元/吨.
对于方案二,设这批水果的平均售价为万元/吨,
由已知数据得,分数在(0,25]内的有17,23,共2个,
所以估计四级水果所占的比例为,
分数在(25,50]内的有27,31,36,40,45,50,共6个,所以估计三级水果所占的比例为,
分数在(50,75]内的有51,51,58,63,65,68,71,共7个,所以估计二级水果所占的比例为,
分数在(75,100]内的有78,79,80,85,95,共5个,所以估计一级水果所占的比例为,
则=1.7.
因为1.8>1.7,所以从经销商的角度考虑,采用方案一较好.
11.解析 (1)设这些人的平均年龄为岁,
则=22.5×0.05+27.5×0.35+32.5×0.3+37.5×0.2+42.5×0.1=32.25.
设第80百分位数为a岁,
因为年龄在[20,25),[25,30),[30,35),[35,40)内的频率分别为0.05,0.35,0.3,0.2,0.05+0.35+0.3=0.7<0.8,0.7+0.2=0.9>0.8,
所以a在区间[35,40)内,
则0.7+(a-35)×0.04=0.8,解得a=37.5.
(2)由题中频率分布直方图可得各组人数之比为1∶7∶6∶4∶2,
故第四组和第五组应分别抽取4人和2人.
设第四组和第五组宣传使者的年龄的平均数分别为岁,岁,方差分别为,则=1.
设第四组和第五组所有宣传使者的年龄的平均数为岁,方差为s2,
则)2]=10.
故这20人中年龄在[35,45]内的所有人的年龄的方差为10.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版高中数学必修第二册同步练习题
综合拔高练
五年高考练
考点1 统计图表的应用
1.(2021全国甲理,2)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是 ( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
2.(多选题)(2020新高考Ⅱ,9)我国新冠肺炎疫情防控进入常态化,各地有序推动复工复产,下面是某地连续11天的复工、复产指数折线图.
根据该折线图,( )
A.这11天复工指数和复产指数均逐日增加
B.在这11天期间,复产指数的增量大于复工指数的增量
C.第3天至第11天,复工指数和复产指数都超过80%
D.第9天至第11天,复产指数的增量大于复工指数的增量
3.(2021天津,4)从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8组:[66,70),[70,74),…,[94,98],并整理得到如下的频率分布直方图,则评分在区间[82,86)内的影视作品数量是( )
A.20 B.40 C.64 D.80
考点2 数字特征的计算及应用
4.(多选题)(2023新课标Ⅰ,9)有一组样本数据x1,x2,…,x6,其中x1是最小值,x6是最大值,则( )
A.x2,x3,x4,x5的平均数等于x1,x2,…,x6的平均数
B.x2,x3,x4,x5的中位数等于x1,x2,…,x6的中位数
C.x2,x3,x4,x5的标准差不小于x1,x2,…,x6的标准差
D.x2,x3,x4,x5的极差不大于x1,x2,…,x6的极差
5.(2022全国甲理,2)某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如下图:
则( )
A.讲座前问卷答题的正确率的中位数小于70%
B.讲座后问卷答题的正确率的平均数大于85%
C.讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D.讲座后问卷答题的正确率的极差大于讲座前正确率的极差
6.(多选题)(2021新高考Ⅱ,9)下列统计量中可用于度量样本x1,x2,…,xn离散程度的有( )
A.x1,x2,…,xn的标准差
B.x1,x2,…,xn的中位数
C.x1,x2,…,xn的极差
D.x1,x2,…,xn的平均数
7.(2020全国Ⅲ文,3)设一组样本数据x1,x2,…,xn的方差为0.01,则数据10x1,10x2,…,10xn的方差为( )
A.0.01 B.0.1 C.1 D.10
8.(多选题)(2021新高考Ⅰ,9)有一组样本数据x1,x2,…,xn,由这组数据得到新样本数据y1,y2,…,yn,其中yi=xi+c(i=1,2,…,n),c为非零常数,则( )
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同
D.两组样本数据的样本极差相同
9.(2020全国Ⅲ理,3)在一组样本数据中,1,2,3,4出现的频率分别为p1,p2,p3,p4,且则下面四种情形中,对应样本的标准差最大的一组是( )
A.p1=p4=0.1,p2=p3=0.4
B.p1=p4=0.4,p2=p3=0.1
C.p1=p4=0.2,p2=p3=0.3
D.p1=p4=0.3,p2=p3=0.2
10.(2023全国乙理,17)某厂为比较甲、乙两种工艺对橡胶产品伸缩率的处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后的橡胶产品的伸缩率.甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为xi,yi(i=1,2,…,10),试验结果如下:
试验 序号i 1 2 3 4 5 6 7 8 9 10
伸缩 率xi 545 533 551 522 575 544 541 568 596 548
伸缩 率yi 536 527 543 530 560 533 522 550 576 536
记zi=xi-yi(i=1,2,…,10),记z1,z2,…,z10的样本平均数为,样本方差为s2.
(1)求,s2;
(2)判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高如果≥2,则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高,否则不认为有显著提高.
11.(2021全国乙理,17)某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备 9.8 10.3 10.0 10.2 9.9
新设备 10.1 10.4 10.1 10.0 10.1
旧设备 9.8 10.0 10.1 10.2 9.7
新设备 10.3 10.6 10.5 10.4 10.5
旧设备和新设备生产产品的该项指标的样本平均数分别记为 ,样本方差分别记为.
(1)求;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高如果≥2,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高.
三年模拟练
应用实践
1.(2023山东泰安模拟)少年强则国强,少年智则国智.党和政府一直重视青少年的健康成长,出台了一系列政策和行动计划,旨在提高学生身体素质.为了加强对学生的营养健康监测,某校在3 000名学生中,抽查了100名学生的体重数据,根据所得数据绘制了样本的频率分布直方图如图所示,则下列结论正确的是(同一组中数据用该组区间中点值作代表)( )
A.样本的众数为65 kg
B.样本的第80百分位数为72.5 kg
C.样本的平均数为67.5 kg
D.该校学生中体重低于65 kg的大约有1 000人
2.(2023浙江绍兴模拟)已知一组样本数据共有9个数,其平均数为8,方差为12.将这组样本数据增加一个数据后,所得新的样本数据的平均数为9,则新的样本数据的方差为( )
A.18.2 B.19.6
C.19.8 D.21.4
3.(2023山东济南实验中学模拟)在高三某次模拟考试中,甲、乙两个班级的数学成绩统计如下表:
班级 人数 平均分 方差
甲 40 70 5
乙 60 80 8
则两个班所有学生的数学成绩的方差为( )
A.6.5 B.13
C.30.8 D.31.8
4.(多选题)(2022山西运城月考)第一组样本数据:x1,x2,…,xn,由这组数据得到第二组样本数据:y1,y2,…,yn,其中yi=axi+b(i=1,2,…,n),a,b为正数,则下列命题正确的是( )
A.当a=1时,两组样本数据的平均数不相同
B.第二组样本数据的极差是第一组的a倍
C.第二组样本数据的标准差是第一组的a倍
D.第二组样本数据的方差是第一组的a倍
5.(多选题)(2023广东潮州模拟)根据气象学上的标准,如果连续5天的日平均气温都低于10 ℃即为入冬.现将连续5天的日平均气温(单位:℃)的记录数据(记录数据都是自然数)作为一组样本,则下列样本中一定符合入冬指标的有( )
A.平均数小于4
B.平均数小于4且极差小于或等于3
C.平均数小于4且标准差小于或等于4
D.众数等于5且极差小于或等于4
6.(多选题)(2022湖南长沙期末)某市2022年经过招商引资后,经济收入较前一年增加了一倍,实现翻番,为更好地了解该市的经济收入变化情况,统计了该市招商引资前后的年经济收入构成比例,得到如下扇形图:
则下列结论中正确的是( )
A.招商引资后,工资净收入较前一年增加
B.招商引资后,转移净收入是前一年的1.25倍
C.招商引资后,转移净收入与财产净收入的总和超过了该年经济收入的
D.招商引资后,经营净收入较前一年增加了一倍
7.(2022安徽淮南模拟)近年来,我国肥胖人群的规模急速增长,肥胖人群有很大的心血管安全隐患.目前,国际上常用身体质量指数(BMI)来衡量人体胖瘦程度以及是否健康,其计算公式是BMI=.我国成人的BMI数值标准为:BMI<18.5为偏瘦,18.5≤BMI<24为正常,24≤BMI<28为偏胖,BMI≥28为肥胖.为了解某公司员工的身体肥胖情况,研究人员从公司员工体检数据中,利用分层随机抽样得到15名员工的BMI数据如下:23.5,21.6,30.6,22.1,23.7,20.6,25.5,23.9,20.8,21.5,21.8,18.2,25.2,21.5,19.1.则该组数据的第70百分位数为 .
8.(2023辽宁沈阳期末)为了解某企业员工对党史的学习情况,对该企业员工进行问卷调查,已知他们的得分都处在A,B,C,D四个区间内,根据调查结果得到下面的统计图.已知该企业男员工占,则下列结论中,正确结论的个数是 .
①男、女员工得分在A区间的占比相同;
②在各得分区间内,男员工的人数都多于女员工的人数;
③得分在C区间的员工最多;
④得分在D区间的员工占总人数的20%.
9.(2023江西五市九校协作体联考)江西省作为全国第四批启动高考综合改革的七个省份之一,从2021年秋季学期起启动实施高考综合改革,实行高考科目“3+1+2”模式.“3”指语文、数学、外语三门统考学科,以原始分计入高考成绩;“1”指考生从物理、历史两门学科中“首选”一门学科,以原始分计入高考成绩;“2”指考生从政治、地理、化学、生物四门学科中“再选”两门学科,以等级分计入高考成绩.按照方案,“再选”学科的等级分赋分规则如下:将考生原始成绩从高到低划分为A,B,C,D,E五个等级,各等级人数所占比例及赋分区间如表,
等级 A B C D E
人数 比例 15% 35% 35% 13% 2%
赋分 区间 [86,100] [71,85] [56,70] [41,55] [30,40]
将各等级内考生的原始分依照等比例转换法分别转换到赋分区间内,得到等级分,转换公式为,其中Y1,Y2分别表示原始分区间的最低分和最高分,T1,T2分别表示等级赋分区间的最低分和最高分,Y表示考生的原始分,T表示考生的等级分,规定原始分为Y1时,等级分为T1,计算结果四舍五入取整.某次化学考试的考生原始分最低分为50,最高分为98,呈连续整数分布,其频率分布直方图如下:
(1)同一组数据以该组区间的中点值作代表,求实数a的值并估计本次考试的平均分;
(2)按照等级分赋分规则,估计此次化学考试成绩中A等级的原始分区间;
(3)用估计的结果近似代替原始分区间,若某学生化学成绩的原始分为90分,试计算其等级分.
10.(2022山西朔州怀仁一中二模)某经销商采购了一批水果,根据某些评价指标进行打分,现从中随机抽取20筐(每筐1 kg),其分数如下:17,23,27,31,36,40,45,50,51,51,58,63,65,68,71,78,79,80,85,95.根据以往的数据认定分数在区间[0,25],(25,50],(50,75],(75,100]内的分别对应四级、三级、二级、一级.
(1)试求这20筐水果分数的平均数;
(2)经销商参考以下两种销售方案对这批水果进行销售:
方案一:按这批水果分数的平均数对应的等级出售;
方案二:按这批水果分数对应的等级出售.
不同等级水果的售价如表所示:
等级 一级 二级 三级 四级
售价 (万元/吨) 2 1.8 1.5 1.2
请从经销商的角度,根据售价分析采用哪种销售方案较好,并说明理由.
11.(2022福建福州期末)某市为了了解人们对“中国梦”的伟大构想的认知程度,针对本市不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(95分及以上为认知程度高),结果认知程度高的有m人,按年龄(单位:岁)分成5组,其中第一组:[20,25),第二组:[25,30),第三组:[30,35),第四组:[35,40),第五组:[40,45],得到如图所示的频率分布直方图.
(1)根据频率分布直方图,估计这些人年龄的平均数和第80百分位数;
(2)现从以上各组中用分层随机抽样的方法抽取20人,担任本市的“中国梦”宣传使者.若第四组宣传使者的年龄的平均数与方差分别为37岁和,第五组宣传使者的年龄的平均数与方差分别为43岁和1,求这20人中年龄在[35,45]内的所有人的年龄的方差.
答案与分层梯度式解析
综合拔高练
五年高考练
1.C 2.CD 3.D 4.BD 5.B 6.AC 7.C 8.CD
9.B
1.C 由题中频率分布直方图可得,该地农户家庭年收入低于4.5万元和不低于10.5万元的频率分别为0.06和0.1,则农户比率分别为6%和10%,故A,B中结论正确;家庭年收入介于4.5万元和8.5万元之间的频率为0.1+0.14+0.2+0.2=0.64,故D中结论正确;家庭年收入的平均值为0.02×3+0.04×4+0.1×5+0.14×6+0.2×7+0.2×8+0.1×9+0.1×10+0.04×11+
0.02×12+0.02×13+0.02×14=7.68(万元),因为7.68>6.5,所以估计该地农户家庭年收入的平均值超过6.5万元,故C中结论不正确.故选C.
2.CD 由题中折线图可知,第7天至第9天,复产指数与复工指数均减少,故选项A错误.在这11天期间,复产指数的增量小于复工指数的增量,故选项B错误.易知C,D正确.故选CD.
3.D 根据题意得,评分在区间[82,86)内的影视作品数量是400×0.05×4=80.故选D.
4.BD 对于A,如1,2,2,2,2,4的平均数不等于2,2,2,2的平均数,故A错误;
对于B,不妨设x2≤x3≤x4≤x5,x2,x3,x4,x5的中位数为,x1,x2,…,x6的中位数为,故B正确;
对于C,x1,x2,…,x6的数据波动性更大,故C错误;
对于D,不妨设x2≤x3≤x4≤x5,则x1≤x2≤x3≤x4≤x5≤x6,所以x5-x2≤x6-x1,故D正确.
故选BD.
5.B 对于A,将讲座前的10个数据从小到大排列依次为60%,60%,65%,65%,70%,75%,80%,85%,90%,95%,易知这10个数据的中位数是第5个与第6个数据的平均数,为=72.5%>70%,故A错误;
对于B,×(90%+85%+80%+90%+85%+85%+95%+100%+85%+100%)=89.5%>85%,故B正确;
对于C,由题图可知,讲座前的数据与讲座后的数据相比,较分散,因此标准差较大,故C错误;
对于D,讲座前问卷答题的正确率的极差为95%-60%=35%,讲座后问卷答题的正确率的极差为100%-80%=20%,20%<35%,故D错误.故选B.
6.AC 由标准差的定义可知,标准差考查的是数据的离散程度;
由中位数的定义可知,中位数考查的是数据的集中趋势;
由极差的定义可知,极差考查的是数据的离散程度;
由平均数的定义可知,平均数考查的是数据的集中趋势.
故选AC.
7.C 根据方差的性质,可得数据10x1,10x2,…,10xn的方差为100×0.01=1,故选C.
8.CD A项,设xi,则xi+c,所以+c,因为c≠0,所以,所以A选项错误.
B项,因为yi=xi+c(i=1,2,…,n),所以y1,y2,…,yn的中位数是x1,x2,…,xn的中位数加c,所以B选项错误.
C项,设)2,
则)2,
所以,所以两组数据的方差相同,从而这两组数据的标准差相同,所以C选项正确.
D项,不妨设x1≤x2≤…≤xn,则第一组数据的极差为xn-x1,另设y1≤y2≤…≤yn,则第二组数据的极差为yn-y1=(xn+c)-(x1+c)=xn-x1,所以两组数据的极差相同,所以D选项正确.故选CD.
9.B 根据平均数方差s2=(xi-)2pi以及方差与标准差的关系,得各选项对应样本的标准差如下表.
选项 平均数 方差s2 标准差s
A 2.5 0.65
B 2.5 1.85
C 2.5 1.05
D 2.5 1.45
由此可知选项B对应样本的标准差最大,故选B.
10.解析 (1)zi=xi-yi(i=1,2,…,10)的值依次为9,6,8,-8,15,11,19,18,20,12,则×(9+6+8-8+15+11+19+18+20+12)=11,
s2=×[(9-11)2+(6-11)2+(8-11)2+(-8-11)2+(15-11)2+(11-11)2+(19-11)2+(18-11)2+(20-11)2+(12-11)2]=61.
(2)由(1)知=11,s2=61,则>0,∴,即甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高.
11.解析 (1)×(9.8+10.3+10.0+10.2+9.9+9.8+10.0+10.1+10.2+9.7)=10.0.
×(10.1+10.4+10.1+10.0+10.1+10.3+10.6+10.5+10.4+10.5)=10.3.
×[(9.8-10.0)2+(10.3-10.0)2+(10.0-10.0)2+(10.2-10.0)2+(9.9-10.0)2+(9.8-10.0)2+(10.0-10.0)2+(10.1-10.0)2+(10.2-10.0)2+(9.7-10.0)2]=0.036.
×[(10.1-10.3)2+(10.4-10.3)2+(10.1-10.3)2+(10.0-10.3)2+(10.1-10.3)2+(10.3-10.3)2+(10.6-10.3)2+(10.5-10.3)2+(10.4-10.3)2+(10.5-10.3)2]=0.04.
(2)由(1)得=0.076,
从而()=0.030 4,所以(,又,故,因此新设备生产产品的该项指标的均值较旧设备有显著提高.
三年模拟练
1.B 2.C 3.C 4.ABC 5.BD 6.AD
1.B 由题中频率分布直方图可得样本的众数为67.5 kg,A错误;
平均数为57.5×0.15+62.5×0.25+67.5×0.3+72.5×0.2+77.5×0.1=66.75(kg),C错误;
因为体重位于[55,60),[60,65),[65,70),[70,75)的频率分别为0.15,0.25,0.3,0.2,0.15+0.25+0.3=0.7<0.8,0.15+0.25+0.3+0.2=0.9>0.8,
所以第80百分位数位于区间[70,75),设第80百分位数为x kg,
则0.7+(x-70)×0.04=0.8,解得x=72.5,
即样本的第80百分位数为72.5 kg,B正确;
样本中低于65 kg的学生的频率为0.15+0.25=0.4,
所以该校学生中体重低于65 kg的大约有3 000×0.4=1 200(人),D错误.
故选B.
2.C 设增加的数为k,原来的9个数分别为a1,a2,…,a9,
则a1+a2+…+a9=72,a1+a2+…+a9+k=90,
所以k=18,
又因为(ai-8)2=12,即(ai-8)2=108,
所以(ai-8)+9+81]=19.8.故选C.
3.C 因为甲班的平均分=70,乙班的平均分=80,
所以两个班所有学生的平均分=76,
所以两个班所有学生的数学成绩的方差s2=×[8+(80-76)2]=30.8.故选C.
4.ABC 设第一组样本数据x1,x2,…,xn的平均数为,方差为s2,
则第二组样本数据ax1+b,ax2+b,…,axn+b的平均数为a+b,方差为a2s2.
对于A选项,当a=1时,第二组样本数据的平均数为+b,因为b>0,所以+b≠,故A正确;
对于B选项,由极差的定义知,若第一组的极差为xmax-xmin,则第二组的极差为ymax-ymin=a(xmax+b)-a(xmin+b)=a(xmax-xmin),即第二组样本数据的极差是第一组的a倍,故B正确;
对于C,D选项,根据方差的性质得,第二组样本数据的方差是第一组的a2倍,则第二组样本数据的标准差是第一组的a倍,故C正确,D错误.
故选ABC.
5.BD 对于A,举反例:0,0,0,0,15,平均数为3,但不符合入冬指标,A错误;
对于B,假设有数据大于或等于10,则由极差小于或等于3知,此组数据中最小的数大于或等于7,与平均数小于4矛盾,故假设不成立,B正确;
对于C,举反例:1,1,1,1,11,平均数为3,且标准差为4,但不符合入冬指标,C错误;
对于D,众数等于5且极差小于或等于4时,最大的数不超过9,D正确.
故选BD.
6.AD 设招商引资前年经济收入为M,则招商引资后年经济收入为2M.
对于A,招商引资前工资净收入为M×60%=0.6M,而招商引资后工资净收入为2M×37%=0.74M,所以工资净收入增加了,故A正确;
对于B,招商引资前转移净收入为M×4%=0.04M,招商引资后转移净收入为2M×5%=0.1M,所以招商引资后,转移净收入是前一年的2.5倍,故B错误;
对于C,招商引资后,转移净收入与财产净收入的总和为0.1M+0.56M=0.66M<×2M=0.8M,所以招商引资后,转移净收入与财产净收入的总和低于该年经济收入的,故C错误;
对于D,招商引资前经营净收入为M×30%=0.3M,招商引资后经营净收入为2M×30%=0.6M,所以招商引资后,经营净收入较前一年增加了一倍,故D正确.
故选AD.
7.答案 23.7
解析 15名员工的BMI数据由小到大排列为18.2,19.1,20.6,20.8,21.5,21.5,21.6,21.8,22.1,23.5,23.7,23.9,25.2,25.5,30.6,
由15×70%=10.5,得该组数据的第70百分位数是第11个数,即23.7.
8.答案 1
解析 设员工总人数为n,
由题中条形图可得女员工人数为20+60+70+50=200,
所以,解得n=500,
所以男员工人数为500-200=300.
对于①,女员工得分在A区间的占比为=10%,男员工得分在A区间的占比为1-40%-35%-15%=10%,故①正确;
对于②,女员工得分在A区间的有20人,B区间的有60人,C区间的有70人,D区间的有50人,
男员工得分在A区间的有300×10%=30(人),B区间的有300×40%=120(人),C区间的有300×35%=105(人),D区间的有300×15%=45(人),
所以D区间男员工的人数少于女员工,故②错误;
对于③,得分在B区间的员工有60+120=180(人),C区间的有70+105=175(人),所以B区间人数比C区间多,故③错误;
对于④,得分在D区间的有50+45=95(人),所以得分在D区间的员工占总人数的×100%=19%,故④错误.
综上,正确结论的个数是1.
9.解析 (1)由题中频率分布直方图可知,(2a+0.04+0.03+0.02)×10=1,解得a=0.005.
估计本次考试的平均分为55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73(分).
(2)A等级所占的人数比例为15%,由题中频率分布直方图知,原始分位于区间[90,100]的占比为5%,位于区间[80,90)的占比为20%,所以最低原始分在[80,90)内,设最低原始分为x,则(90-x)×0.02=15%-5%,解得x=85,所以估计此次化学考试成绩中A等级的原始分区间为[85,98].
(3)由(2)知,化学成绩的原始分为90分是A等级,则T1=86,T2=100,Y1=85,Y2=98,Y=90,代入公式,得,解得T=≈91,故该学生的等级分为91分.
10.解析 (1)这20筐水果分数的平均数为×(17+23+27+31+36+40+45+50+51+51+58+63+65+68+71+78+79+80+85+95)=55.65.
(2)采用方案一较好.理由如下:
对于方案一,由于分数的平均数为55.65,对应二级,所以可以估计这批水果的售价为1.8万元/吨.
对于方案二,设这批水果的平均售价为万元/吨,
由已知数据得,分数在(0,25]内的有17,23,共2个,
所以估计四级水果所占的比例为,
分数在(25,50]内的有27,31,36,40,45,50,共6个,所以估计三级水果所占的比例为,
分数在(50,75]内的有51,51,58,63,65,68,71,共7个,所以估计二级水果所占的比例为,
分数在(75,100]内的有78,79,80,85,95,共5个,所以估计一级水果所占的比例为,
则=1.7.
因为1.8>1.7,所以从经销商的角度考虑,采用方案一较好.
11.解析 (1)设这些人的平均年龄为岁,
则=22.5×0.05+27.5×0.35+32.5×0.3+37.5×0.2+42.5×0.1=32.25.
设第80百分位数为a岁,
因为年龄在[20,25),[25,30),[30,35),[35,40)内的频率分别为0.05,0.35,0.3,0.2,0.05+0.35+0.3=0.7<0.8,0.7+0.2=0.9>0.8,
所以a在区间[35,40)内,
则0.7+(a-35)×0.04=0.8,解得a=37.5.
(2)由题中频率分布直方图可得各组人数之比为1∶7∶6∶4∶2,
故第四组和第五组应分别抽取4人和2人.
设第四组和第五组宣传使者的年龄的平均数分别为岁,岁,方差分别为,则=1.
设第四组和第五组所有宣传使者的年龄的平均数为岁,方差为s2,
则)2]=10.
故这20人中年龄在[35,45]内的所有人的年龄的方差为10.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
