2024人教版高中数学必修第二册同步练习题--第九章 统计复习提升(含解析)
文档属性
| 名称 | 2024人教版高中数学必修第二册同步练习题--第九章 统计复习提升(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024人教版高中数学必修第二册同步练习题
本章复习提升
易混易错练
易错点1 在分层随机抽样中忽视抽样比或者权重致错
1.(2021天津河西期末)某中学高一、高二、高三年级的学生人数之比为6∶5∶7,防疫站欲对该校学生进行身体健康调查,用比例分配的分层随机抽样方法从该校三个年级的学生中抽取一个容量为n的样本,已知样本中高三年级的学生有21人,则n=( )
A.35 B.45 C.54 D.63
2.(2023湖南长沙长郡中学一模)为调查某地区中学生每天的睡眠时间,采用样本量按比例分配的分层随机抽样,现抽取初中生800人,其每天睡眠时间的均值为9小时,方差为1,抽取高中生1 200人,其每天睡眠时间的均值为8小时,方差为0.5,则估计该地区中学生每天睡眠时间的方差为( )
A.0.96 B.0.94 C.0.79 D.0.75
3.(2022山西一模)某校要求每名学生只参加一个兴趣小组,并对高一、高二年级的3个兴趣小组的学生人数进行了统计,结果如下表:
书法组 舞蹈组 乐器组
高一 x 20 30
高二 45 30 10
已知按兴趣小组类别用比例分配的分层随机抽样的方法从参加这3个兴趣小组的学生中抽取30人,其中书法组被抽取了12人,则x= .
易错点2 使用频率分布直方图解题时把纵坐标当成频率而致错
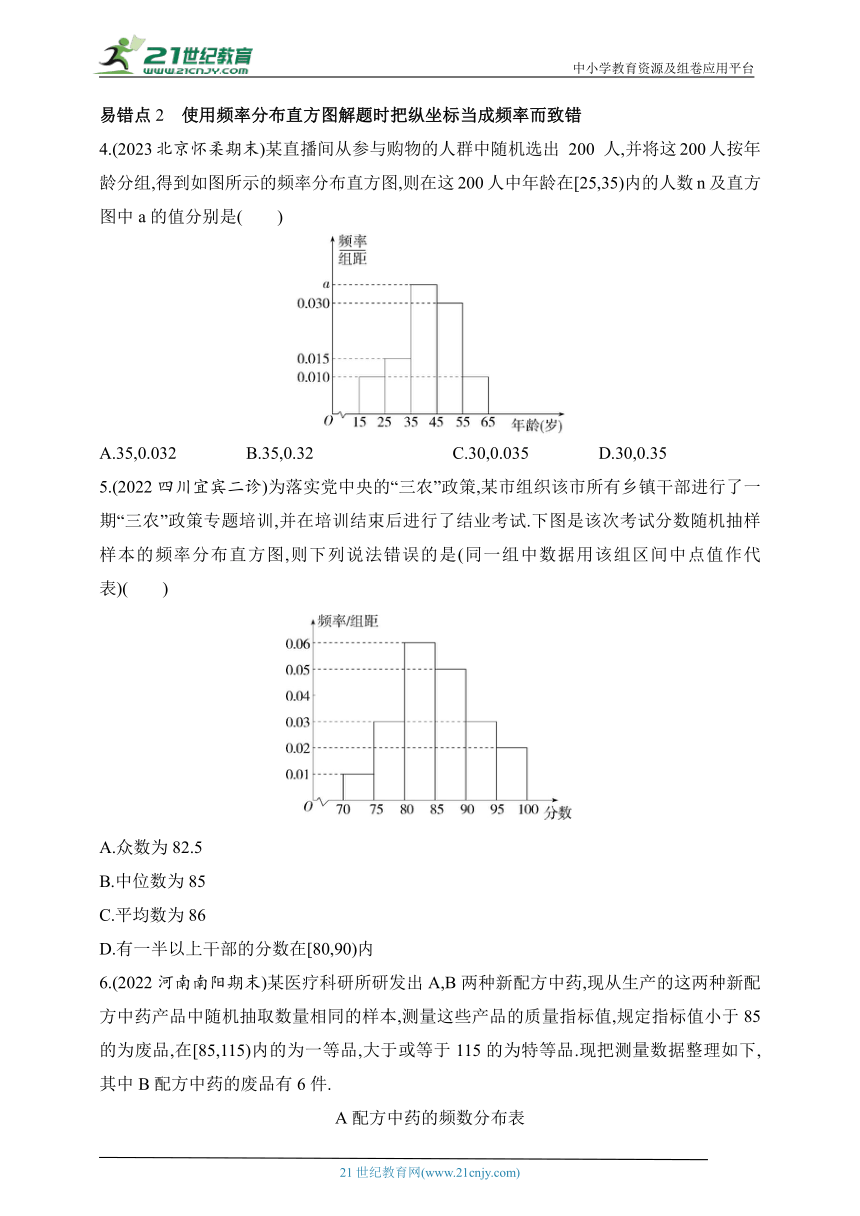
4.(2023北京怀柔期末)某直播间从参与购物的人群中随机选出 200 人,并将这200人按年龄分组,得到如图所示的频率分布直方图,则在这200人中年龄在[25,35)内的人数n及直方图中a的值分别是( )
A.35,0.032 B.35,0.32 C.30,0.035 D.30,0.35
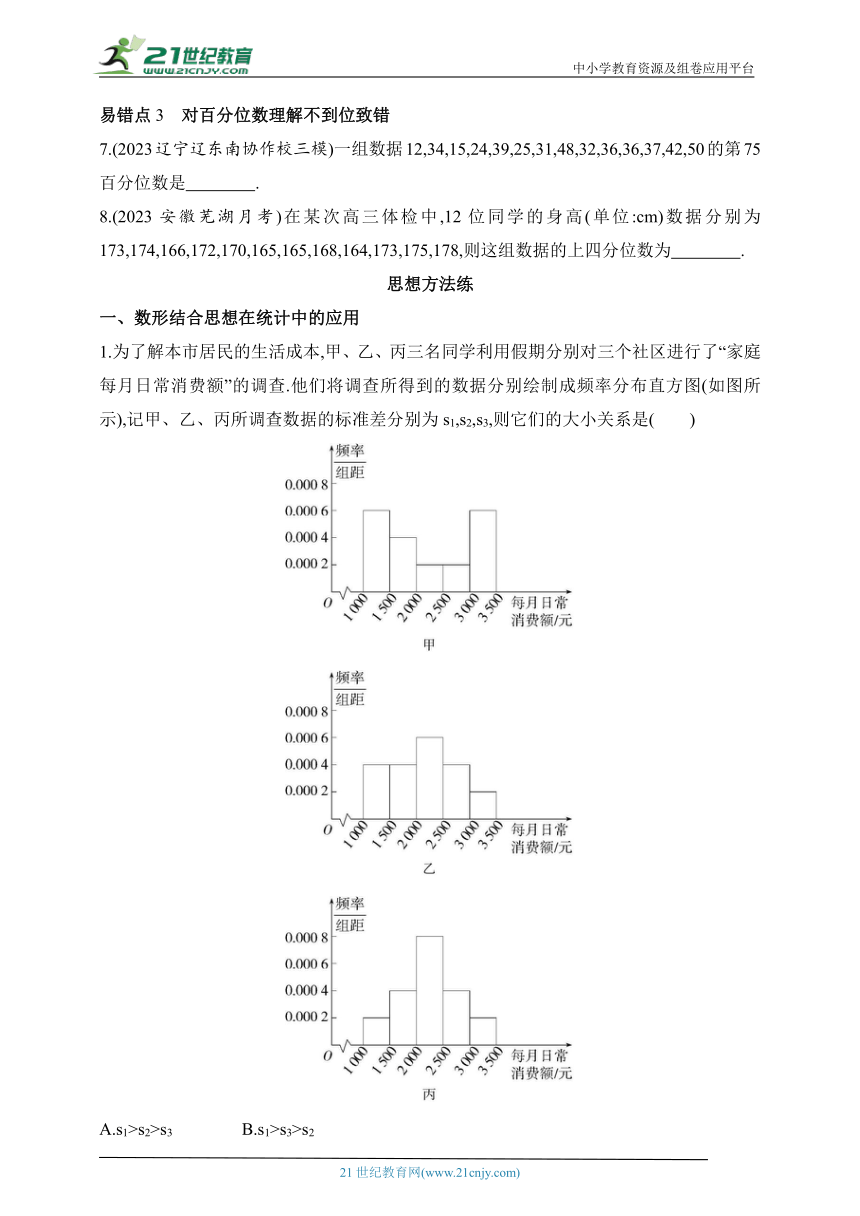
5.(2022四川宜宾二诊)为落实党中央的“三农”政策,某市组织该市所有乡镇干部进行了一期“三农”政策专题培训,并在培训结束后进行了结业考试.下图是该次考试分数随机抽样样本的频率分布直方图,则下列说法错误的是(同一组中数据用该组区间中点值作代表)( )
A.众数为82.5
B.中位数为85
C.平均数为86
D.有一半以上干部的分数在[80,90)内
6.(2022河南南阳期末)某医疗科研所研发出A,B两种新配方中药,现从生产的这两种新配方中药产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于85的为废品,在[85,115)内的为一等品,大于或等于115的为特等品.现把测量数据整理如下,其中B配方中药的废品有6件.
A配方中药的频数分布表
质量 指标值 [75, 85) [85, 95) [95, 105) [105, 115) [115, 125]
频数 8 a 36 24 8
(1)求a,b的值;
(2)若从A,B两种新配方中药中选择一种进行推广,试确定推广哪种比较好.(同一组中的数据用该组区间的中点值作代表)
易错点3 对百分位数理解不到位致错
7.(2023辽宁辽东南协作校三模)一组数据12,34,15,24,39,25,31,48,32,36,36,37,42,50的第75百分位数是 .
8.(2023安徽芜湖月考)在某次高三体检中,12位同学的身高(单位:cm)数据分别为173,174,166,172,170,165,165,168,164,173,175,178,则这组数据的上四分位数为 .
思想方法练
一、数形结合思想在统计中的应用
1.为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为s1,s2,s3,则它们的大小关系是( )
A.s1>s2>s3 B.s1>s3>s2
C.s3>s2>s1 D.s3>s1>s2
2.(多选题)(2023湖北孝感期中)某保险公司为客户制订了5个险种,甲:一年期短险;乙:两全保险;丙:理财类保险;丁:定期寿险;戊:重大疾病保险.各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得到的统计图如图所示,以下四个选项中正确的有( )
A.54周岁及以上的参保人数最少
B.18~29周岁参保客户的总费用最少
C.丁险种最受参保客户青睐
D.30周岁及以上的参保客户占参保客户的80%
二、函数与方程思想在统计中的应用
3.(2023广东河源期末)某校为了了解高三年级学生的身体素质状况,在开学初举行了一场身体素质体能测试,以便对体能不达标的学生进行针对性的训练,促进他们体能的提升,现从整个年级测试成绩中抽取100名学生的测试成绩,并把测试成绩分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组,绘制成频率分布直方图(如图所示),其中[90,100]这一组对应的纵坐标为a,则该次体能测试成绩的80%分位数约为 分.
4.(2022江苏南通金沙中学期末)设样本数据x1,x2,…,x2 022的平均数为,方差为s2,若数据2(x1+1),2(x2+1),…,2(x2 022+1)的平均数比方差大4,求s2-的最大值.
答案与分层梯度式解析
易混易错练
1.C 2.B 4.C 5.C
1.C ∵该中学高一、高二、高三年级的学生人数之比为6∶5∶7,∴高三年级学生人数占总人数的,
∵用比例分配的分层随机抽样方法从该校三个年级的学生中抽取一个容量为n的样本,且高三年级被抽取的人数为21,∴n=21÷=54.
故选C.
易错警示 解决有关分层随机抽样的问题时,先根据题目条件得出或计算出相应比例,或者各部分的权重,再列式求解.
2.B 该地区中学生每天睡眠时间的均值为×8=8.4(小时),
则该地区中学生每天睡眠时间的方差为×[0.5+(8-8.4)2]=0.94.
故选B.
3.答案 15
解析 由题意得×30=12,解得x=15.
4.C 由题中频率分布直方图知,年龄在[25,35)内的频率为0.015×10=0.15,
所以年龄在[25,35)内的人数n=0.15×200=30,
由频率分布直方图的小矩形的面积和为1,可得0.01×10+0.015×10+a×10+0.03×10+0.01×10=1,
解得a=0.035.故选C.
5.C 由题中频率分布直方图知众数为82.5,A中说法正确;
(0.01+0.03+0.06)×5=0.5,故中位数为85,B中说法正确;
平均数为(0.01×72.5+0.03×77.5+0.06×82.5+0.05×87.5+0.03×92.5+0.02×97.5)×5=85.5,C中说法错误;
由(0.06+0.05)×5=0.55>0.5,知有一半以上干部的分数在[80,90)内,D中说法正确.
故选C.
6.解析 (1)依题意,A,B两种新配方中药的样本容量相同,设为n,
因为B配方中药的废品有6件,
所以=0.006×10,解得n=100,
则a=100-(8+36+24+8)=24.
由(0.006+b+0.038+0.022+0.008)×10=1,解得b=0.026.
(2)A配方中药的质量指标值的平均数×(80×8+90×24+100×36+110×24+120×8)=100,
方差×[(-20)2×8+(-10)2×24+102×24+202×8]=112.
B配方中药的质量指标值的平均数=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100,
方差=(-20)2×0.06+(-10)2×0.26+102×0.22+202×0.08=104.
综上,,即两种配方中药的质量指标值的平均数相等,但B配方中药的质量指标值比A配方中药的稳定,所以选择B配方中药进行推广比较好.
易错警示 利用频率分布直方图解决相关问题时,要注意纵坐标并不是频率,而是,频率分布直方图中小矩形的面积才是频率.
7.答案 39
解析 将数据由小到大排列,得12,15,24,25,31,32,34,36,36,37,39,42,48,
50,共14个数据,
由14×75%=10.5,得第75百分位数是39.
易错警示 当计算n个数据的第p百分位数时,首先按从小到大排列原始数据;然后计算i=n×p%,若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据.
8.答案 173.5
解析 将12个数据从小到大排列,可得164,165,165,166,168,170,172,
173,173,174,175,178,而12×75%=9,
故这组数据的上四分位数为第9个和第10个数据的平均数,即=173.5.
思想方法练
1.A 观察题中三个频率分布直方图,可得
甲的数据绝大部分都处在两端,数据大多离平均数远,表现得最分散,所以其标准差最大;
乙的数据分布均匀,数据偏离平均数的程度比甲低,故其标准差比甲的标准差小;
丙的数据绝大部分都在平均数左右,数据最集中,所以其标准差最小.
所以s1>s2>s3,故选A.
2.ACD 由题中扇形图可知54周岁及以上的参保客户所占的比例最少,故参保人数最少,故A选项正确;
由题中折线图可知18~29周岁的参保客户人均参保费用最少,但这类人所占比例不是最少的,故总费用不一定最少,故B选项错误;
由题中条形图可知丁险种的参保比例最高,故最受参保客户青睐,故C选项正确;
由题中扇形图可知30周岁及以上的参保客户所占比例为1-20%=80%,故D选项正确.故选ACD.
由条形图得到参保各险种的比例,由扇形图得到各年龄段参保人数比例,由折线图可估计各年龄段的参保费用.利用所读取的数据解决相关问题.
思想方法 数形结合思想在统计问题中的应用:一方面用图形直观表示相关统计量,另一方面借助图形直观比较相关统计量的关系,要熟练运用条形图、扇形图、折线图、频率分布直方图解决相关统计问题.
3.答案 92
解析 根据频率分布直方图中小矩形的面积之和为1,列方程.
由(0.002+0.004+0.014+0.020+0.035+a)×10=1,解得a=0.025.
因为0.02+0.04+0.14+0.2+0.35=0.75,
所以该次体能测试成绩的80%分位数落在[90,100]内,设80%分位数为x分,
根据百分位数的定义,列方程.
则(x-90)×0.025=0.8-0.75,解得x=92.
4.解析 根据平均数和方差的性质,可得数据2(x1+1),2(x2+1),…,
2(x2 022+1)的平均数为2(+1),方差为22s2=4s2.
根据题意列式,将s2-的一元二次函数,利用二次函数的性质求最值.
由题意得,2(+1)-4s2=4,即s2=,
则s2-.
利用方差的性质求的取值范围.
因为s2≥0,所以≥0,即≥1,故当=1时,s2-取得最大值,最大值是-1.
思想方法 在统计中,利用相关计算公式列出方程(组),进而解决统计问题是一种最基本的方法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版高中数学必修第二册同步练习题
本章复习提升
易混易错练
易错点1 在分层随机抽样中忽视抽样比或者权重致错
1.(2021天津河西期末)某中学高一、高二、高三年级的学生人数之比为6∶5∶7,防疫站欲对该校学生进行身体健康调查,用比例分配的分层随机抽样方法从该校三个年级的学生中抽取一个容量为n的样本,已知样本中高三年级的学生有21人,则n=( )
A.35 B.45 C.54 D.63
2.(2023湖南长沙长郡中学一模)为调查某地区中学生每天的睡眠时间,采用样本量按比例分配的分层随机抽样,现抽取初中生800人,其每天睡眠时间的均值为9小时,方差为1,抽取高中生1 200人,其每天睡眠时间的均值为8小时,方差为0.5,则估计该地区中学生每天睡眠时间的方差为( )
A.0.96 B.0.94 C.0.79 D.0.75
3.(2022山西一模)某校要求每名学生只参加一个兴趣小组,并对高一、高二年级的3个兴趣小组的学生人数进行了统计,结果如下表:
书法组 舞蹈组 乐器组
高一 x 20 30
高二 45 30 10
已知按兴趣小组类别用比例分配的分层随机抽样的方法从参加这3个兴趣小组的学生中抽取30人,其中书法组被抽取了12人,则x= .
易错点2 使用频率分布直方图解题时把纵坐标当成频率而致错
4.(2023北京怀柔期末)某直播间从参与购物的人群中随机选出 200 人,并将这200人按年龄分组,得到如图所示的频率分布直方图,则在这200人中年龄在[25,35)内的人数n及直方图中a的值分别是( )
A.35,0.032 B.35,0.32 C.30,0.035 D.30,0.35
5.(2022四川宜宾二诊)为落实党中央的“三农”政策,某市组织该市所有乡镇干部进行了一期“三农”政策专题培训,并在培训结束后进行了结业考试.下图是该次考试分数随机抽样样本的频率分布直方图,则下列说法错误的是(同一组中数据用该组区间中点值作代表)( )
A.众数为82.5
B.中位数为85
C.平均数为86
D.有一半以上干部的分数在[80,90)内
6.(2022河南南阳期末)某医疗科研所研发出A,B两种新配方中药,现从生产的这两种新配方中药产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于85的为废品,在[85,115)内的为一等品,大于或等于115的为特等品.现把测量数据整理如下,其中B配方中药的废品有6件.
A配方中药的频数分布表
质量 指标值 [75, 85) [85, 95) [95, 105) [105, 115) [115, 125]
频数 8 a 36 24 8
(1)求a,b的值;
(2)若从A,B两种新配方中药中选择一种进行推广,试确定推广哪种比较好.(同一组中的数据用该组区间的中点值作代表)
易错点3 对百分位数理解不到位致错
7.(2023辽宁辽东南协作校三模)一组数据12,34,15,24,39,25,31,48,32,36,36,37,42,50的第75百分位数是 .
8.(2023安徽芜湖月考)在某次高三体检中,12位同学的身高(单位:cm)数据分别为173,174,166,172,170,165,165,168,164,173,175,178,则这组数据的上四分位数为 .
思想方法练
一、数形结合思想在统计中的应用
1.为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为s1,s2,s3,则它们的大小关系是( )
A.s1>s2>s3 B.s1>s3>s2
C.s3>s2>s1 D.s3>s1>s2
2.(多选题)(2023湖北孝感期中)某保险公司为客户制订了5个险种,甲:一年期短险;乙:两全保险;丙:理财类保险;丁:定期寿险;戊:重大疾病保险.各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得到的统计图如图所示,以下四个选项中正确的有( )
A.54周岁及以上的参保人数最少
B.18~29周岁参保客户的总费用最少
C.丁险种最受参保客户青睐
D.30周岁及以上的参保客户占参保客户的80%
二、函数与方程思想在统计中的应用
3.(2023广东河源期末)某校为了了解高三年级学生的身体素质状况,在开学初举行了一场身体素质体能测试,以便对体能不达标的学生进行针对性的训练,促进他们体能的提升,现从整个年级测试成绩中抽取100名学生的测试成绩,并把测试成绩分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组,绘制成频率分布直方图(如图所示),其中[90,100]这一组对应的纵坐标为a,则该次体能测试成绩的80%分位数约为 分.
4.(2022江苏南通金沙中学期末)设样本数据x1,x2,…,x2 022的平均数为,方差为s2,若数据2(x1+1),2(x2+1),…,2(x2 022+1)的平均数比方差大4,求s2-的最大值.
答案与分层梯度式解析
易混易错练
1.C 2.B 4.C 5.C
1.C ∵该中学高一、高二、高三年级的学生人数之比为6∶5∶7,∴高三年级学生人数占总人数的,
∵用比例分配的分层随机抽样方法从该校三个年级的学生中抽取一个容量为n的样本,且高三年级被抽取的人数为21,∴n=21÷=54.
故选C.
易错警示 解决有关分层随机抽样的问题时,先根据题目条件得出或计算出相应比例,或者各部分的权重,再列式求解.
2.B 该地区中学生每天睡眠时间的均值为×8=8.4(小时),
则该地区中学生每天睡眠时间的方差为×[0.5+(8-8.4)2]=0.94.
故选B.
3.答案 15
解析 由题意得×30=12,解得x=15.
4.C 由题中频率分布直方图知,年龄在[25,35)内的频率为0.015×10=0.15,
所以年龄在[25,35)内的人数n=0.15×200=30,
由频率分布直方图的小矩形的面积和为1,可得0.01×10+0.015×10+a×10+0.03×10+0.01×10=1,
解得a=0.035.故选C.
5.C 由题中频率分布直方图知众数为82.5,A中说法正确;
(0.01+0.03+0.06)×5=0.5,故中位数为85,B中说法正确;
平均数为(0.01×72.5+0.03×77.5+0.06×82.5+0.05×87.5+0.03×92.5+0.02×97.5)×5=85.5,C中说法错误;
由(0.06+0.05)×5=0.55>0.5,知有一半以上干部的分数在[80,90)内,D中说法正确.
故选C.
6.解析 (1)依题意,A,B两种新配方中药的样本容量相同,设为n,
因为B配方中药的废品有6件,
所以=0.006×10,解得n=100,
则a=100-(8+36+24+8)=24.
由(0.006+b+0.038+0.022+0.008)×10=1,解得b=0.026.
(2)A配方中药的质量指标值的平均数×(80×8+90×24+100×36+110×24+120×8)=100,
方差×[(-20)2×8+(-10)2×24+102×24+202×8]=112.
B配方中药的质量指标值的平均数=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100,
方差=(-20)2×0.06+(-10)2×0.26+102×0.22+202×0.08=104.
综上,,即两种配方中药的质量指标值的平均数相等,但B配方中药的质量指标值比A配方中药的稳定,所以选择B配方中药进行推广比较好.
易错警示 利用频率分布直方图解决相关问题时,要注意纵坐标并不是频率,而是,频率分布直方图中小矩形的面积才是频率.
7.答案 39
解析 将数据由小到大排列,得12,15,24,25,31,32,34,36,36,37,39,42,48,
50,共14个数据,
由14×75%=10.5,得第75百分位数是39.
易错警示 当计算n个数据的第p百分位数时,首先按从小到大排列原始数据;然后计算i=n×p%,若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据.
8.答案 173.5
解析 将12个数据从小到大排列,可得164,165,165,166,168,170,172,
173,173,174,175,178,而12×75%=9,
故这组数据的上四分位数为第9个和第10个数据的平均数,即=173.5.
思想方法练
1.A 观察题中三个频率分布直方图,可得
甲的数据绝大部分都处在两端,数据大多离平均数远,表现得最分散,所以其标准差最大;
乙的数据分布均匀,数据偏离平均数的程度比甲低,故其标准差比甲的标准差小;
丙的数据绝大部分都在平均数左右,数据最集中,所以其标准差最小.
所以s1>s2>s3,故选A.
2.ACD 由题中扇形图可知54周岁及以上的参保客户所占的比例最少,故参保人数最少,故A选项正确;
由题中折线图可知18~29周岁的参保客户人均参保费用最少,但这类人所占比例不是最少的,故总费用不一定最少,故B选项错误;
由题中条形图可知丁险种的参保比例最高,故最受参保客户青睐,故C选项正确;
由题中扇形图可知30周岁及以上的参保客户所占比例为1-20%=80%,故D选项正确.故选ACD.
由条形图得到参保各险种的比例,由扇形图得到各年龄段参保人数比例,由折线图可估计各年龄段的参保费用.利用所读取的数据解决相关问题.
思想方法 数形结合思想在统计问题中的应用:一方面用图形直观表示相关统计量,另一方面借助图形直观比较相关统计量的关系,要熟练运用条形图、扇形图、折线图、频率分布直方图解决相关统计问题.
3.答案 92
解析 根据频率分布直方图中小矩形的面积之和为1,列方程.
由(0.002+0.004+0.014+0.020+0.035+a)×10=1,解得a=0.025.
因为0.02+0.04+0.14+0.2+0.35=0.75,
所以该次体能测试成绩的80%分位数落在[90,100]内,设80%分位数为x分,
根据百分位数的定义,列方程.
则(x-90)×0.025=0.8-0.75,解得x=92.
4.解析 根据平均数和方差的性质,可得数据2(x1+1),2(x2+1),…,
2(x2 022+1)的平均数为2(+1),方差为22s2=4s2.
根据题意列式,将s2-的一元二次函数,利用二次函数的性质求最值.
由题意得,2(+1)-4s2=4,即s2=,
则s2-.
利用方差的性质求的取值范围.
因为s2≥0,所以≥0,即≥1,故当=1时,s2-取得最大值,最大值是-1.
思想方法 在统计中,利用相关计算公式列出方程(组),进而解决统计问题是一种最基本的方法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
