函数的图象
图片预览





文档简介
课件25张PPT。复习回顾:一、两种量:变量和常量
二、函数的定义:如果有两个变量X、Y, 对于X的每一个取值,Y都有唯一的值与之对应,则称X是自变量,Y是应变量,称Y是X的函数。
三、函数的表示方法:
1、图象法; 2、列表法;
3、解析法;(注意书写格式和要注明 自变量的取值范围)
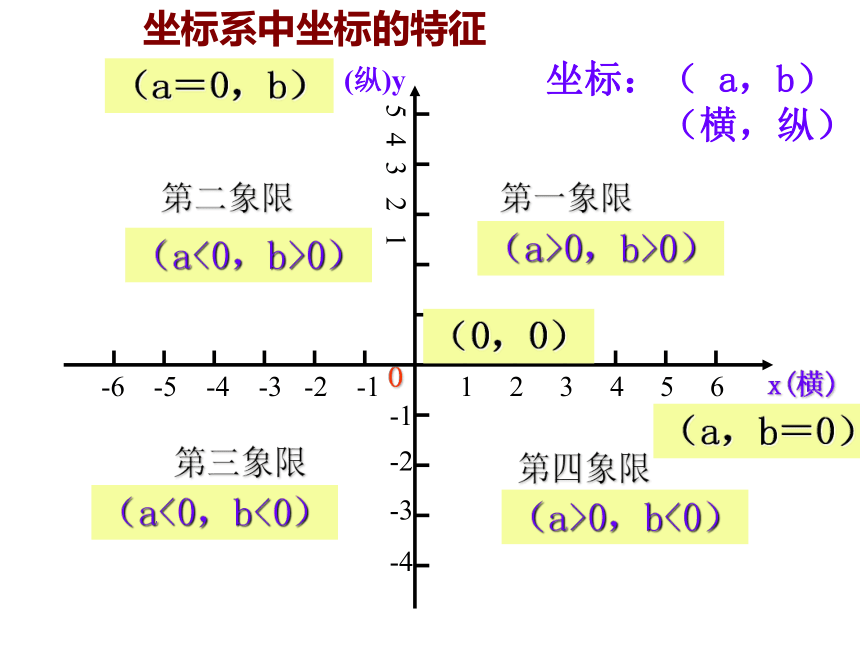
四、直角坐标系 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6x(横)(纵)yO第一象限第二象限第三象限第四象限坐标系中坐标的特征(a>0,b<0)(a<0,b<0)(a<0,b>0)(a>0,b>0)坐标:( a,b)
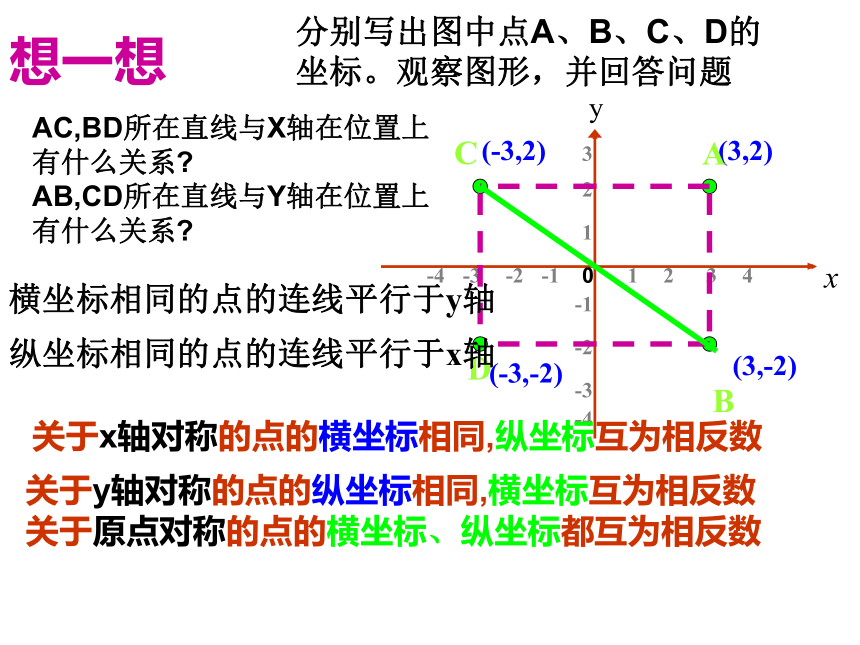
(横,纵)(a=0,b)(a,b=0)(0,0)想一想分别写出图中点A、B、C、D的坐标。观察图形,并回答问题(3,2)(3,-2)-2-14321-3-4-4y123-3-1-2(-3,2)(-3,-2)0关于x轴对称的点的横坐标相同,纵坐标互为相反数关于y轴对称的点的纵坐标相同,横坐标互为相反数关于原点对称的点的横坐标、纵坐标都互为相反数A BCD纵坐标相同的点的连线平行于x轴横坐标相同的点的连线平行于y轴AC,BD所在直线与X轴在位置上
有什么关系?
AB,CD所在直线与Y轴在位置上
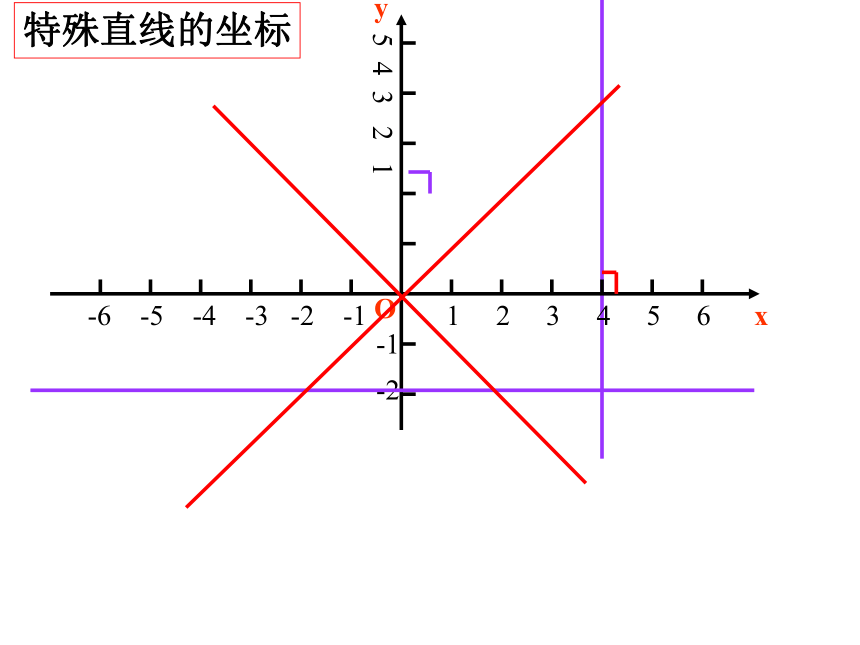
有什么关系? -6 -5 -4 -3 -2 -1 1 2 3 4 5 6xyO特殊直线的坐标八年级数学函数的图象(1)教学目标
1,了解函数图象的意义,学会用描点法画
出函数图象.
2,掌握解析法与图象法表示函数关系的相互转换,会从图形中分析变量的关系.
3,进一步体会数形结合思想在数学学习中的作用,通过实际操作,提高识
图和画图的能力,树立运动变化的观念
重点:了解函数图象的意义,用描点法画出函数图象.
难点:描点法画出函数图象这一气温曲线实际上给出了某日的气温T(℃)与时间t(时)的函数关系.气温曲线是用图象表示函数的一个实际例子.
那么,什么是函数的图象呢?
例如,上午10时的气温是2℃,表现在X气温曲线上,就是可以找到这样的对应点,它的坐标是(10, 2).实质上也就是说,当t=10时,对应的函数值T=2.气温曲线上每一个点的坐标(t,T),表示时间为t时的气温是T
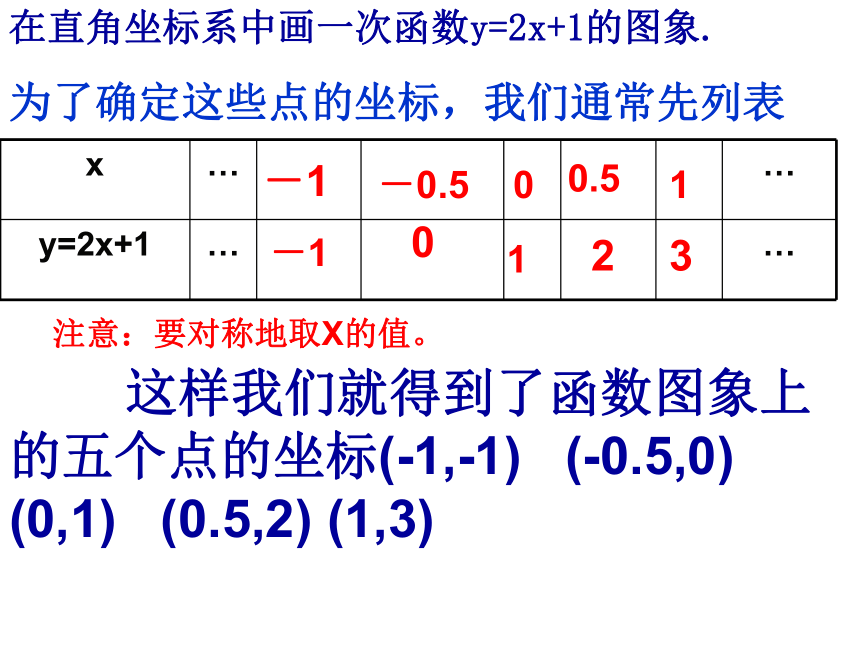
一般来说,函数的图象是由直角坐标系中的一系列点组成.图象上每一点的坐标(x,y)代表了函数的一对对应值,它的横坐标x表示自变量的某一个值,纵坐标y表示与它对应的函数值什么是函数图象?如何画出已知函数的图象?为了确定这些点的坐标,我们通常先列表 这样我们就得到了函数图象上的五个点的坐标(-1,-1) (-0.5,0) (0,1) (0.5,2) (1,3)在直角坐标系中画一次函数y=2x+1的图象.注意:要对称地取X的值。在直角坐标系中画一次函数y=2x+1的图象.?????y=2x+1⑴.列表:⑵.描点
在直角坐标系中,描出这些有序实数对(坐标)的对应点, :
(-1,-1) (-0.5,0) (0,1) (0.5,2) (1,3)
⑶.连线.为什么要“连线”?怎样连线?4注意:要对称地取X的值,这样有什么好处呢?画函数图象的这种方法,通常称为描点法.⑴列表; ⑵描点; ⑶连线.画 函数图象的一般步骤:练 习
在所给的直角坐标系中画出函数y= x的图象
(先填写下表,再描点、连线).-101y=2x+1 和y= x的图象
有什么共同点?都是一条直线结论:一次函数的图象是一条直线2.画出函数y= 的图象236-6-3-2问题1
王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图18.2.6中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时),看图回答下列问题:
小强让爷爷先上多少米?2,山顶高多少米?谁先爬上山顶.3,从图中,你还能看出什么问题? 60米300米练 习
1.下图为世界总人口数的变化图.根据该图回答:
从1830年到1998年,世界总人口数呈怎样的变化趋势?2,在图中,显示哪一段时间中世界总人口数变化最快?1976-19872.一枝蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则下列3幅图象中能大致刻画出这枝蜡烛点燃后剩下的长度h(厘米)与点燃时间t之间的函数关系的是( ).C3.小明从家里出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家.
下面的图描述了小明在散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系.
你能根据图象说出小明散步过程中的一些具体信息吗?练一练:函数y=2x+3的图象是( )
(A)过点(0,3),(0, )的直线(D)过点(0,3),( ,0)的直线(B)过点(0, ),(1,5)的直线(C)过点( ,0),( ,1)的直线CABCB(2)B4.甲、乙两人在一次赛跑中,路程与时间的关系如图所示,那么可以知道:①这是一次________米赛路;②甲、乙两人先到达终点的是_________;③在这次赛跑中甲的速度为________,乙的速度为________.
5.如图所示,表示的是某航空公司托运行李的费用y(元)与托运行李的质量x(千克)的关系,由图中可知行李的质量只要不超过_________千克,就可以免费托运.100甲米/秒8米/秒
20 例:已知有两人分别骑自行车和摩托车沿着相同的路线从甲地到乙地去,下图反映的是这两个人行驶过程中时间和路程的关系,请根据图象回答下列问题:
(1)甲地与乙地相距多少千米?两个人分别用了几小时才到达乙地?谁先到达了乙地?早到多长时间?(2)分别描述在这个过程中自行车和摩托车的行驶状态.解:(1)甲地与乙地相距100千米.两个人分别用了2小时(骑摩托车)、6小时(骑自行车)到达乙地.骑摩托车的先到乙地,早到了1小时.(2)骑自行车的先匀速行驶了2小时,行驶40千米后休息了1小时,然后用3小时到达乙地.骑摩托车的在自行车出发3小时后出发,行驶2小时后到达乙地.(3)摩托车行驶的平均速度是50千米/时.
(3)求摩托车行驶的平均速度.解:(1)从图象中观察得知:自变量X的取值范围是:0≤x≤5(2)从图象中观察得知:当 x = 3 时,y 有最小值,最小值 y = 2.5(3)从图象中观察得知:y 随着 x 的增大而增大。作业课外作业:完成课本
P.37 4,P38 5,6
同步作业:P20-21
二、函数的定义:如果有两个变量X、Y, 对于X的每一个取值,Y都有唯一的值与之对应,则称X是自变量,Y是应变量,称Y是X的函数。
三、函数的表示方法:
1、图象法; 2、列表法;
3、解析法;(注意书写格式和要注明 自变量的取值范围)
四、直角坐标系 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6x(横)(纵)yO第一象限第二象限第三象限第四象限坐标系中坐标的特征(a>0,b<0)(a<0,b<0)(a<0,b>0)(a>0,b>0)坐标:( a,b)
(横,纵)(a=0,b)(a,b=0)(0,0)想一想分别写出图中点A、B、C、D的坐标。观察图形,并回答问题(3,2)(3,-2)-2-14321-3-4-4y123-3-1-2(-3,2)(-3,-2)0关于x轴对称的点的横坐标相同,纵坐标互为相反数关于y轴对称的点的纵坐标相同,横坐标互为相反数关于原点对称的点的横坐标、纵坐标都互为相反数A BCD纵坐标相同的点的连线平行于x轴横坐标相同的点的连线平行于y轴AC,BD所在直线与X轴在位置上
有什么关系?
AB,CD所在直线与Y轴在位置上
有什么关系? -6 -5 -4 -3 -2 -1 1 2 3 4 5 6xyO特殊直线的坐标八年级数学函数的图象(1)教学目标
1,了解函数图象的意义,学会用描点法画
出函数图象.
2,掌握解析法与图象法表示函数关系的相互转换,会从图形中分析变量的关系.
3,进一步体会数形结合思想在数学学习中的作用,通过实际操作,提高识
图和画图的能力,树立运动变化的观念
重点:了解函数图象的意义,用描点法画出函数图象.
难点:描点法画出函数图象这一气温曲线实际上给出了某日的气温T(℃)与时间t(时)的函数关系.气温曲线是用图象表示函数的一个实际例子.
那么,什么是函数的图象呢?
例如,上午10时的气温是2℃,表现在X气温曲线上,就是可以找到这样的对应点,它的坐标是(10, 2).实质上也就是说,当t=10时,对应的函数值T=2.气温曲线上每一个点的坐标(t,T),表示时间为t时的气温是T
一般来说,函数的图象是由直角坐标系中的一系列点组成.图象上每一点的坐标(x,y)代表了函数的一对对应值,它的横坐标x表示自变量的某一个值,纵坐标y表示与它对应的函数值什么是函数图象?如何画出已知函数的图象?为了确定这些点的坐标,我们通常先列表 这样我们就得到了函数图象上的五个点的坐标(-1,-1) (-0.5,0) (0,1) (0.5,2) (1,3)在直角坐标系中画一次函数y=2x+1的图象.注意:要对称地取X的值。在直角坐标系中画一次函数y=2x+1的图象.?????y=2x+1⑴.列表:⑵.描点
在直角坐标系中,描出这些有序实数对(坐标)的对应点, :
(-1,-1) (-0.5,0) (0,1) (0.5,2) (1,3)
⑶.连线.为什么要“连线”?怎样连线?4注意:要对称地取X的值,这样有什么好处呢?画函数图象的这种方法,通常称为描点法.⑴列表; ⑵描点; ⑶连线.画 函数图象的一般步骤:练 习
在所给的直角坐标系中画出函数y= x的图象
(先填写下表,再描点、连线).-101y=2x+1 和y= x的图象
有什么共同点?都是一条直线结论:一次函数的图象是一条直线2.画出函数y= 的图象236-6-3-2问题1
王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图18.2.6中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时),看图回答下列问题:
小强让爷爷先上多少米?2,山顶高多少米?谁先爬上山顶.3,从图中,你还能看出什么问题? 60米300米练 习
1.下图为世界总人口数的变化图.根据该图回答:
从1830年到1998年,世界总人口数呈怎样的变化趋势?2,在图中,显示哪一段时间中世界总人口数变化最快?1976-19872.一枝蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则下列3幅图象中能大致刻画出这枝蜡烛点燃后剩下的长度h(厘米)与点燃时间t之间的函数关系的是( ).C3.小明从家里出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家.
下面的图描述了小明在散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系.
你能根据图象说出小明散步过程中的一些具体信息吗?练一练:函数y=2x+3的图象是( )
(A)过点(0,3),(0, )的直线(D)过点(0,3),( ,0)的直线(B)过点(0, ),(1,5)的直线(C)过点( ,0),( ,1)的直线CABCB(2)B4.甲、乙两人在一次赛跑中,路程与时间的关系如图所示,那么可以知道:①这是一次________米赛路;②甲、乙两人先到达终点的是_________;③在这次赛跑中甲的速度为________,乙的速度为________.
5.如图所示,表示的是某航空公司托运行李的费用y(元)与托运行李的质量x(千克)的关系,由图中可知行李的质量只要不超过_________千克,就可以免费托运.100甲米/秒8米/秒
20 例:已知有两人分别骑自行车和摩托车沿着相同的路线从甲地到乙地去,下图反映的是这两个人行驶过程中时间和路程的关系,请根据图象回答下列问题:
(1)甲地与乙地相距多少千米?两个人分别用了几小时才到达乙地?谁先到达了乙地?早到多长时间?(2)分别描述在这个过程中自行车和摩托车的行驶状态.解:(1)甲地与乙地相距100千米.两个人分别用了2小时(骑摩托车)、6小时(骑自行车)到达乙地.骑摩托车的先到乙地,早到了1小时.(2)骑自行车的先匀速行驶了2小时,行驶40千米后休息了1小时,然后用3小时到达乙地.骑摩托车的在自行车出发3小时后出发,行驶2小时后到达乙地.(3)摩托车行驶的平均速度是50千米/时.
(3)求摩托车行驶的平均速度.解:(1)从图象中观察得知:自变量X的取值范围是:0≤x≤5(2)从图象中观察得知:当 x = 3 时,y 有最小值,最小值 y = 2.5(3)从图象中观察得知:y 随着 x 的增大而增大。作业课外作业:完成课本
P.37 4,P38 5,6
同步作业:P20-21
