2.3匀变速直线运动的位移与时间的关系 (共29张PPT) 课件-高一上学期物理人教版(2019)必修第一册
文档属性
| 名称 | 2.3匀变速直线运动的位移与时间的关系 (共29张PPT) 课件-高一上学期物理人教版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 38.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-10 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
匀变速直线运动的位移与时间关系
导入新课
3世纪中期,魏晋时期的数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法,所谓割圆术,就是不断倍增圆内接正多边形的边数求出圆周率的方法。其基本原理是:越是把圆周分割得细,其内接正多边形的周长就越是接近圆周。如此不断地分割下去,一直到圆周无法再分割为止,也就是到了圆内接正多边形的边数无限多的时候,它的周长就与圆周"合体"而完全一致了。查阅相关材料(观看视频),说明其中蕴含的科学研究的思想。
观看视频:南沙永署礁新建机场飞机试飞:舰载机起飞、降落。思考:
1、在海岛上建飞机跑道为什么要吹砂填海?
2、舰载机起飞必须达到一定的速度,为什么舰载机起飞时要利用弹射装置,降落时要用拦阻索?
3、位移也是运动中重要的物理量,匀变速运动位移与哪些因素有关?
导入新课
匀速直线运动的位移与时间的关系
☆交流讨论
1. 图甲为匀速直线运动的速度-时间图像,根据匀速直线运动的位移公式讨论一下,它代表了哪个物理量?如图所示,阴影部分的面积在数值上与物体在2s内的位移是什么关系?
v(m/s)
t/s
10
2
t/s
2. 图乙为匀速直线运动的速度-时间图像,根据匀速直线运动的位移公式讨论一下,它与图甲的区别和联系。
甲
v(m/s)
乙
-10
2
☆梳理深化
1、在匀速直线运动中,v-t图象的面积可代表对应时间间隔内的位移。
2、时间轴上方速度、位移为正,表示速度、位移的方向与规定的正方向相同;时间轴下方速度、位移为负 ,表示速度、位移的方向与规定的正方向相反。
匀速直线运动的位移与时间的关系
☆巩固提升
例、一物体在水平面上沿直线运动,速度随时间的变化关系如图所示,请计算物体在3s内发生的位移。
解析:s=s1+s2+s3=4×1+8×1+12×1=24m
匀速直线运动的位移与时间的关系
t/s
v/(m/s)
0 1 2 3
12
8
4
探究用v-t图像能否表示匀变速直线运动的位移
粗略地表示位移
较精确地表示位移
匀变速直线运动的位移
无限分割,逐渐逼近的极限思想
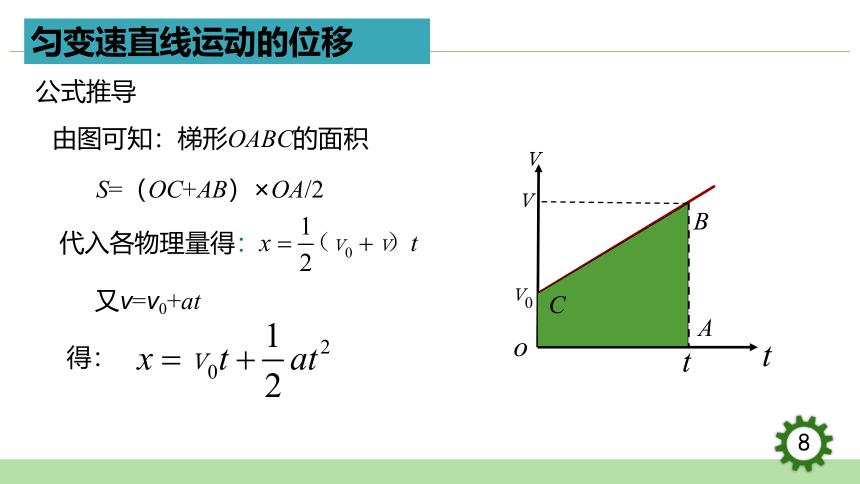
梯形OABC的面积就代表做匀变速直线运动物体在0(此时速度为v0)到t(此时速度为v)这段时间的位移。
由图可知:梯形OABC的面积
S=(OC+AB)×OA/2
又v=v0+at
匀变速直线运动的位移
公式推导
C
B
A
得:
代入各物理量得:
对位移公式 的理解:
⑴反映了位移随时间的变化规律。
⑵因为υ0、a、x均为矢量,使用公式时应先规定正方向。(一般以υ0的方向为正方向)若物体做匀加速运动,a取正值,若物体做匀减速运动,则a取负值。
(3)若v0=0,则x=
(4)特别提醒: t是指物体运动的实际时间,要将位移与发生这段位移的时间对应起来。
v0
v
0
t
v0
v
0
t
v0
v
0
t
v0
v
0
t
在每一小段内,可粗略认为物体做匀速直线运动。
各段位移可以用一个又窄又高的小矩形的面积代表。
小矩形的面积之和近似地代表物体在整个运动过程中的位移。
微元求和
t时间内位移等于图像中的梯形面积
这种分析问题的方法具有一般意义,原则上对于处理任意形状的v-t图像都适用。
【例】物体从静止开始做匀加速直线运动,加速度为1m/s2,求:
(1)物体在2s内的位移;
(2)物体在第2s内的位移;
(3)物体在第二个2s内的位移。
应用位移公式解题的一般步骤
(1)确定一个方向为正方向(一般以初速度的方向为正方向)。
(2)根据规定的正方向确定已知量的正、负,并用带有正、负的数值表示。
(3)根据位移—时间关系式或其变形式列式、求解。
(4)根据计算结果说明所求量的大小、方向。
【例】汽车沿平直公路匀减速刹车,初速度大小为7m/s,第1s内的位移大小为6m,求:
(1)汽车刹车的加速度大小;
(2)汽车刹车后4s内的位移大小。
☆交流讨论
由前面的学习我们知道,描述运动的五个物理量——初速度、末速度、位移、时间、加速度相互影响,相互制约,你能根据已掌握的匀变速运动位移公式和速度公式推导速度位移公式吗?
匀变速直线运动的速度与位移的关系
消去时间t
对速度位移公式 的理解
☆梳理深化
1. 公式优势:因公式v2-v02=2ax不涉及物体运动的时间,故在不要求计算时间时,应用该式分析匀变速直线运动较简便
2.适用条件:匀变速直线运动
3.矢量性:v2-v02=2ax为矢量式,x、v0、a都是矢量,应用时必须选取统一的正方向,一般选初速度v0的方向为正方向。
(1)匀加速直线运动,a取正值;匀减速直线运动,a取负值
(2)位移与正方向相同,取正值;位移与正方向相反,取负值
匀变速直线运动的速度与位移的关系
v
0
t
2T
v0
v2T
vT
T
x2-x1=aT .T=aT2
x3-x2=aT .T=aT2
x2-x1=x3-x2=x4-x3=…..=aT2
同理可证:
利用图象证明位移差公式
利用图象证明位移差公式
xm-xn=(m-n)aT2
【课堂反馈】在一事故现场,交警测量一汽车刹车后滑行的位移为32m,已知汽车的加速度为4m/s2,若此路段限速为36km/h,则该汽车是否超速?
x=16 m
V0?
a=-4m/s2
V=0
解析:取向右为正方向
根据题意可知:a=-4 m/s2
末速度为V=0 位移为x=16 m
V0=16m/s
36km/h
=10m/s
>
超速
注意!!
公式的矢量性:公式中v0、v、a、x都是矢量,应用时必须选取统一的正方向,一般选v0方向为正方向。
(1)物体做加速运动时,a取正值,做减速运动时,a取负值。
(2)x>0,说明物体通过的位移方向与初速度方向相同;x<0,说明位移的方向与初速度的方向相反。
实验次数 1 2
刹车前速度(km/h) 20 90
刹车痕迹长度(m) 2.0 40.0
【课堂反馈】下表是王芳同学探究车辆制动距离的试验,假设车辆刹车过程做匀减速直线运动,请根据表中的数据,求出每次实验刹车过程中的加速度。
解:
1、飞机在跑道上滑行,离地起飞时的速度是60 m/s,若飞机滑行时加速度大小为4 m/s2,则飞机从开始滑行至起飞需时间————s,起飞的跑道长至少为————m。
课堂练习
2、某物体的初速度为2 m/s,在4 s的时间内速度均匀增大到6m/s,那么该物体在这段时间内发生的位移x为————m。
15
450
16
课堂练习
3、某航母跑道长200m,飞机在航母上滑行的最大加速度为6m/s2,起飞需要的最低速度为50m/s,那么,飞机在滑行前,需要借助弹射系统获得的最小初速度为( )
A.5m/s
B.10m/s
C.15m/s
D.20m/s
B
课堂练习
4、汽车以20 m/s的速度做匀速直线运动,刹车后的加速度为5 m/s2,那么开始刹车后2 s与开始刹车后6s汽车通过的位移分别为多少?
课堂练习
5、汽车以20 m/s的速度做匀速直线运动,刹车后的加速度为5 m/s2,那么开始刹车后2 s与开始刹车后6s汽车通过的位移之比为( )
A.1︰4
B.3︰5
C.3︰4
D.5︰9
C
拓展提高
B
1、做匀变速直线运动的物体的速度v随位移x的变化规律v2-4=2x,v与x的单位分别为m/s和m,据此可知( )
A.初速度v0=4m/s
B.初速度v0=2m/s
C.加速度a=-1m/s2
D.加速度a=2m/s2
2、一质点沿一直线运动,t=0时,位于坐标原点,下图为质点做直线运动的速度时间图象.由图可知:
(1)该质点的位移随时间变化的关系式是:x=____________。
(2)在时刻t=____s时,质点距坐标原点最远。
(3)从t=0到t=20 s内质点的位移是______;
通过的路程是_______。
-4t+0.2t2
10
0 m
40 m
拓展提高
v/(m s-1)
t/s
匀变速直线运动的位移与时间关系
导入新课
3世纪中期,魏晋时期的数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法,所谓割圆术,就是不断倍增圆内接正多边形的边数求出圆周率的方法。其基本原理是:越是把圆周分割得细,其内接正多边形的周长就越是接近圆周。如此不断地分割下去,一直到圆周无法再分割为止,也就是到了圆内接正多边形的边数无限多的时候,它的周长就与圆周"合体"而完全一致了。查阅相关材料(观看视频),说明其中蕴含的科学研究的思想。
观看视频:南沙永署礁新建机场飞机试飞:舰载机起飞、降落。思考:
1、在海岛上建飞机跑道为什么要吹砂填海?
2、舰载机起飞必须达到一定的速度,为什么舰载机起飞时要利用弹射装置,降落时要用拦阻索?
3、位移也是运动中重要的物理量,匀变速运动位移与哪些因素有关?
导入新课
匀速直线运动的位移与时间的关系
☆交流讨论
1. 图甲为匀速直线运动的速度-时间图像,根据匀速直线运动的位移公式讨论一下,它代表了哪个物理量?如图所示,阴影部分的面积在数值上与物体在2s内的位移是什么关系?
v(m/s)
t/s
10
2
t/s
2. 图乙为匀速直线运动的速度-时间图像,根据匀速直线运动的位移公式讨论一下,它与图甲的区别和联系。
甲
v(m/s)
乙
-10
2
☆梳理深化
1、在匀速直线运动中,v-t图象的面积可代表对应时间间隔内的位移。
2、时间轴上方速度、位移为正,表示速度、位移的方向与规定的正方向相同;时间轴下方速度、位移为负 ,表示速度、位移的方向与规定的正方向相反。
匀速直线运动的位移与时间的关系
☆巩固提升
例、一物体在水平面上沿直线运动,速度随时间的变化关系如图所示,请计算物体在3s内发生的位移。
解析:s=s1+s2+s3=4×1+8×1+12×1=24m
匀速直线运动的位移与时间的关系
t/s
v/(m/s)
0 1 2 3
12
8
4
探究用v-t图像能否表示匀变速直线运动的位移
粗略地表示位移
较精确地表示位移
匀变速直线运动的位移
无限分割,逐渐逼近的极限思想
梯形OABC的面积就代表做匀变速直线运动物体在0(此时速度为v0)到t(此时速度为v)这段时间的位移。
由图可知:梯形OABC的面积
S=(OC+AB)×OA/2
又v=v0+at
匀变速直线运动的位移
公式推导
C
B
A
得:
代入各物理量得:
对位移公式 的理解:
⑴反映了位移随时间的变化规律。
⑵因为υ0、a、x均为矢量,使用公式时应先规定正方向。(一般以υ0的方向为正方向)若物体做匀加速运动,a取正值,若物体做匀减速运动,则a取负值。
(3)若v0=0,则x=
(4)特别提醒: t是指物体运动的实际时间,要将位移与发生这段位移的时间对应起来。
v0
v
0
t
v0
v
0
t
v0
v
0
t
v0
v
0
t
在每一小段内,可粗略认为物体做匀速直线运动。
各段位移可以用一个又窄又高的小矩形的面积代表。
小矩形的面积之和近似地代表物体在整个运动过程中的位移。
微元求和
t时间内位移等于图像中的梯形面积
这种分析问题的方法具有一般意义,原则上对于处理任意形状的v-t图像都适用。
【例】物体从静止开始做匀加速直线运动,加速度为1m/s2,求:
(1)物体在2s内的位移;
(2)物体在第2s内的位移;
(3)物体在第二个2s内的位移。
应用位移公式解题的一般步骤
(1)确定一个方向为正方向(一般以初速度的方向为正方向)。
(2)根据规定的正方向确定已知量的正、负,并用带有正、负的数值表示。
(3)根据位移—时间关系式或其变形式列式、求解。
(4)根据计算结果说明所求量的大小、方向。
【例】汽车沿平直公路匀减速刹车,初速度大小为7m/s,第1s内的位移大小为6m,求:
(1)汽车刹车的加速度大小;
(2)汽车刹车后4s内的位移大小。
☆交流讨论
由前面的学习我们知道,描述运动的五个物理量——初速度、末速度、位移、时间、加速度相互影响,相互制约,你能根据已掌握的匀变速运动位移公式和速度公式推导速度位移公式吗?
匀变速直线运动的速度与位移的关系
消去时间t
对速度位移公式 的理解
☆梳理深化
1. 公式优势:因公式v2-v02=2ax不涉及物体运动的时间,故在不要求计算时间时,应用该式分析匀变速直线运动较简便
2.适用条件:匀变速直线运动
3.矢量性:v2-v02=2ax为矢量式,x、v0、a都是矢量,应用时必须选取统一的正方向,一般选初速度v0的方向为正方向。
(1)匀加速直线运动,a取正值;匀减速直线运动,a取负值
(2)位移与正方向相同,取正值;位移与正方向相反,取负值
匀变速直线运动的速度与位移的关系
v
0
t
2T
v0
v2T
vT
T
x2-x1=aT .T=aT2
x3-x2=aT .T=aT2
x2-x1=x3-x2=x4-x3=…..=aT2
同理可证:
利用图象证明位移差公式
利用图象证明位移差公式
xm-xn=(m-n)aT2
【课堂反馈】在一事故现场,交警测量一汽车刹车后滑行的位移为32m,已知汽车的加速度为4m/s2,若此路段限速为36km/h,则该汽车是否超速?
x=16 m
V0?
a=-4m/s2
V=0
解析:取向右为正方向
根据题意可知:a=-4 m/s2
末速度为V=0 位移为x=16 m
V0=16m/s
36km/h
=10m/s
>
超速
注意!!
公式的矢量性:公式中v0、v、a、x都是矢量,应用时必须选取统一的正方向,一般选v0方向为正方向。
(1)物体做加速运动时,a取正值,做减速运动时,a取负值。
(2)x>0,说明物体通过的位移方向与初速度方向相同;x<0,说明位移的方向与初速度的方向相反。
实验次数 1 2
刹车前速度(km/h) 20 90
刹车痕迹长度(m) 2.0 40.0
【课堂反馈】下表是王芳同学探究车辆制动距离的试验,假设车辆刹车过程做匀减速直线运动,请根据表中的数据,求出每次实验刹车过程中的加速度。
解:
1、飞机在跑道上滑行,离地起飞时的速度是60 m/s,若飞机滑行时加速度大小为4 m/s2,则飞机从开始滑行至起飞需时间————s,起飞的跑道长至少为————m。
课堂练习
2、某物体的初速度为2 m/s,在4 s的时间内速度均匀增大到6m/s,那么该物体在这段时间内发生的位移x为————m。
15
450
16
课堂练习
3、某航母跑道长200m,飞机在航母上滑行的最大加速度为6m/s2,起飞需要的最低速度为50m/s,那么,飞机在滑行前,需要借助弹射系统获得的最小初速度为( )
A.5m/s
B.10m/s
C.15m/s
D.20m/s
B
课堂练习
4、汽车以20 m/s的速度做匀速直线运动,刹车后的加速度为5 m/s2,那么开始刹车后2 s与开始刹车后6s汽车通过的位移分别为多少?
课堂练习
5、汽车以20 m/s的速度做匀速直线运动,刹车后的加速度为5 m/s2,那么开始刹车后2 s与开始刹车后6s汽车通过的位移之比为( )
A.1︰4
B.3︰5
C.3︰4
D.5︰9
C
拓展提高
B
1、做匀变速直线运动的物体的速度v随位移x的变化规律v2-4=2x,v与x的单位分别为m/s和m,据此可知( )
A.初速度v0=4m/s
B.初速度v0=2m/s
C.加速度a=-1m/s2
D.加速度a=2m/s2
2、一质点沿一直线运动,t=0时,位于坐标原点,下图为质点做直线运动的速度时间图象.由图可知:
(1)该质点的位移随时间变化的关系式是:x=____________。
(2)在时刻t=____s时,质点距坐标原点最远。
(3)从t=0到t=20 s内质点的位移是______;
通过的路程是_______。
-4t+0.2t2
10
0 m
40 m
拓展提高
v/(m s-1)
t/s
