2023-2024学年人教A版数学选择性必修一同步测试1.1.1 空间向量及其线性运算(含答案)
文档属性
| 名称 | 2023-2024学年人教A版数学选择性必修一同步测试1.1.1 空间向量及其线性运算(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 362.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 00:00:00 | ||
图片预览




文档简介
第一章 空间向量与立体几何
1.1 空间向量及其运算
1.1.1 空间向量及其线性运算
一.选择题
1.下列说法中,错误的是( )
A.向量与的长度相等
B.两个相等的向量,若起点相同,则终点也相同
C.只有零向量的模等于0
D.共线的单位向量都相等
2.下列关于单位向量与零向量的叙述正确的是( )
A.零向量是没有方向的向量,两个单位向量的模相等
B.零向量的方向是任意的,所有单位向量都相等
C.零向量的长度为0,单位向量不一定是相等向量
D.零向量只有一个方向,模相等的单位向量的方向不一定相同
3.(多选)下列说法正确的有( )
A.若A,B,C,D是不共线的四点,则=是四边形ABCD是平行四边形的充要条件
B.若a=b,b=c,则a=c
C.向量a,b相等的充要条件是
D.=的充要条件是A与C重合,B与D重合
4.如图所示空间四边形ABCD,连接AC,BD,设M,G分别是BC,CD的中点,则-+等于( )
A. B.3
C.3 D.2
5.已知正方体ABCD-A1B1C1D1中,=,若=x+y(+),则( )
A.x=1,y= B.x=,y=1
C.x=1,y= D.x=1,y=
6.设空间四点O,A,B,P满足=m+n,其中m+n=1,则( )
A.点P一定在直线AB上
B.点P一定不在直线AB上
C.点P可能在直线AB上,也可能不在直线AB上
D.与的方向一定相同
7.以下说法正确的为( )
A.方向相反的两个向量是相反向量
B.若a,b满足|a|>|b|且a,b同向,则a>b
C.不相等的两个空间向量的模必不相等
D.对于任何向量a,b,必有|a+b|≤|a|+|b|
8.对于空间的任意三个向量a,b,2a-b,它们一定是( )
A.共面向量
B.共线向量
C.不共面向量
D.既不共线也不共面的向量
9.如图,已知平行六面体ABCD-A1B1C1D1,在下列选项中,与相等的向量是( )
A. B.
C. D.
10.在三棱柱ABC-A1B1C1中,D是CC1的中点,F是A1B的中点,且=α+β,则( )
A.α=,β=-1
B.α=-,β=1
C.α=1,β=-
D.α=-1,β=
11.(多选)设A,B,C是空间任意三点,下列结论正确的是( )
A.+= B.++=0
C.-= D.=-
二、填空题
12.在四边形ABCD中,若=+,则四边形ABCD的形状一定是________.
13. 已知M,N分别是四面体OABC的棱OA,BC的中点,点P在线段MN上,且MP=2PN,设向量=a,O=b,O=c,则O=________.
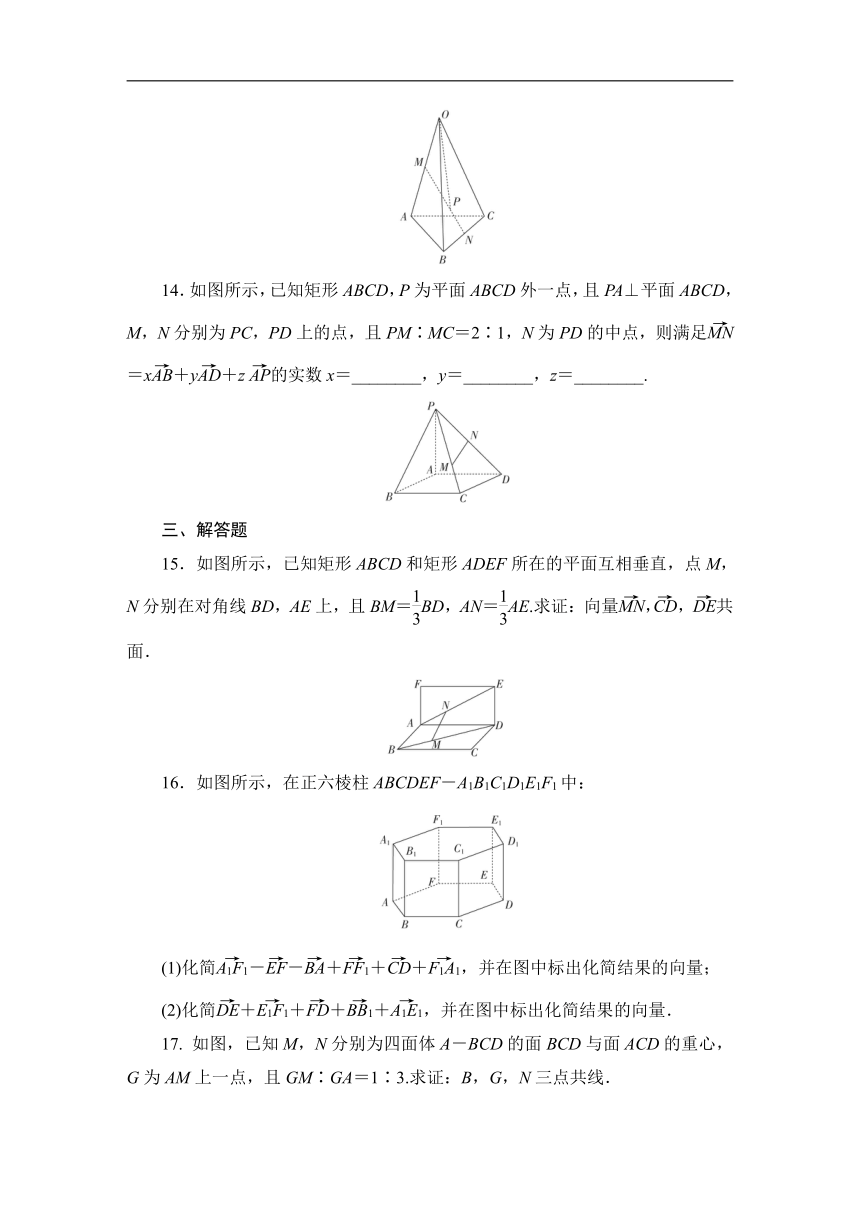
14.如图所示,已知矩形ABCD,P为平面ABCD外一点,且PA⊥平面ABCD,M,N分别为PC,PD上的点,且PM∶MC=2∶1,N为PD的中点,则满足=x+y+z的实数x=________,y=________,z=________.
三、解答题
15.如图所示,已知矩形ABCD和矩形ADEF所在的平面互相垂直,点M,N分别在对角线BD,AE上,且BM=BD,AN=AE.求证:向量,,共面.
16.如图所示,在正六棱柱ABCDEF-A1B1C1D1E1F1中:
(1)化简--+++,并在图中标出化简结果的向量;
(2)化简++++,并在图中标出化简结果的向量.
17. 如图,已知M,N分别为四面体A-BCD的面BCD与面ACD的重心,G为AM上一点,且GM∶GA=1∶3.求证:B,G,N三点共线.
第一章 空间向量与立体几何
1.1 空间向量及其运算
1.1.1 空间向量及其线性运算
一.选择题
1.下列说法中,错误的是( )
A.向量与的长度相等
B.两个相等的向量,若起点相同,则终点也相同
C.只有零向量的模等于0
D.共线的单位向量都相等
答案 D
解析 共线的单位向量是相等向量或相反向量.
2.下列关于单位向量与零向量的叙述正确的是( )
A.零向量是没有方向的向量,两个单位向量的模相等
B.零向量的方向是任意的,所有单位向量都相等
C.零向量的长度为0,单位向量不一定是相等向量
D.零向量只有一个方向,模相等的单位向量的方向不一定相同
答案 C
解析 因为零向量的方向是任意的,且长度为0,两个单位向量的模相等,但方向不一定相同.故选C.
3.(多选)下列说法正确的有( )
A.若A,B,C,D是不共线的四点,则=是四边形ABCD是平行四边形的充要条件
B.若a=b,b=c,则a=c
C.向量a,b相等的充要条件是
D.=的充要条件是A与C重合,B与D重合
答案 AB
解析 A正确,∵=,∴||=||且∥.又A,B,C,D不共线,∴四边形ABCD是平行四边形.反之,在 ABCD中,有=;B正确,∵a=b,∴a,b的长度相等且方向相同.∵b=c,∴b,c的长度相等且方向相同.故a=c;C不正确,由a∥b,知a与b的方向相同或相反;D显然不正确.故选AB.
4.如图所示空间四边形ABCD,连接AC,BD,设M,G分别是BC,CD的中点,则-+等于( )
A. B.3
C.3 D.2
答案 B
解析 -+=-(-)=-=+=+2=3.故选B.
5.已知正方体ABCD-A1B1C1D1中,=,若=x+y(+),则( )
A.x=1,y= B.x=,y=1
C.x=1,y= D.x=1,y=
答案 D
解析 因为=+=+=+(+),所以x=1,y=.
6.设空间四点O,A,B,P满足=m+n,其中m+n=1,则( )
A.点P一定在直线AB上
B.点P一定不在直线AB上
C.点P可能在直线AB上,也可能不在直线AB上
D.与的方向一定相同
答案 A
解析 已知m+n=1,则m=1-n,所以=(1-n)+n=-n+n -=n(-) =n.因为≠0,所以和共线,即点A,P,B共线.故选A.
7.以下说法正确的为( )
A.方向相反的两个向量是相反向量
B.若a,b满足|a|>|b|且a,b同向,则a>b
C.不相等的两个空间向量的模必不相等
D.对于任何向量a,b,必有|a+b|≤|a|+|b|
答案 D
解析 长度相等且方向相反的两个向量是相反向量,故A错误;向量是不能比较大小的,故B错误;不相等的两个空间向量的模也可以相等,故C错误;由向量加法的几何意义可知D正确.故选D.
8.对于空间的任意三个向量a,b,2a-b,它们一定是( )
A.共面向量
B.共线向量
C.不共面向量
D.既不共线也不共面的向量
答案 A
解析 记c=2a-b,由共面向量的判定方法易知,a,b,c三个向量是共面向量.故选A.
9.如图,已知平行六面体ABCD-A1B1C1D1,在下列选项中,与相等的向量是( )
A. B.
C. D.
答案 C
解析 由于ABCD-A1B1C1D1是平行六面体,所以||=||,且与方向相同,故=.故选C.
10.在三棱柱ABC-A1B1C1中,D是CC1的中点,F是A1B的中点,且=α+β,则( )
A.α=,β=-1
B.α=-,β=1
C.α=1,β=-
D.α=-1,β=
答案 A
解析 根据向量加法的多边形法则以及已知可得,=++=++=+-++=-,∴α=,β=-1.故选A.
11.(多选)设A,B,C是空间任意三点,下列结论正确的是( )
A.+= B.++=0
C.-= D.=-
答案 ACD
解析 B中向量的和应该是零向量,而不是数0,B错误;由空间向量的线性运算法则,知A,C,D正确.故选ACD.
二、填空题
12.在四边形ABCD中,若=+,则四边形ABCD的形状一定是________.
答案 平行四边形
解析 因为=+,所以四边形ABCD是以AB与AD为邻边,AC为对角线的平行四边形.
13. 已知M,N分别是四面体OABC的棱OA,BC的中点,点P在线段MN上,且MP=2PN,设向量=a,O=b,O=c,则O=________.
答案 a+b+c
解析 ∵MP=2PN,
∴M=2P,
即O-O=2(O-O),
3O=O+2O=a+b+c,
∴O=a+b+c.
14.如图所示,已知矩形ABCD,P为平面ABCD外一点,且PA⊥平面ABCD,M,N分别为PC,PD上的点,且PM∶MC=2∶1,N为PD的中点,则满足=x+y+z的实数x=________,y=________,z=________.
答案 - -
解析 如图所示,在PD上取一点F,使PF∶FD=2∶1,连接MF,则=+.
∵=-=-==(-),===-,
∴=--+,
∴x=-,y=-,z=.
三、解答题
15.如图所示,已知矩形ABCD和矩形ADEF所在的平面互相垂直,点M,N分别在对角线BD,AE上,且BM=BD,AN=AE.求证:向量,,共面.
证明 因为M在BD上,且BM=BD,
所以==+.
同理=+.
所以=++
=++
=+=+.
又与不共线,根据向量共面的充要条件可知,,共面.
16.如图所示,在正六棱柱ABCDEF-A1B1C1D1E1F1中:
(1)化简--+++,并在图中标出化简结果的向量;
(2)化简++++,并在图中标出化简结果的向量.
解 (1)--+++=+++++=++0=+=.
在图中所示如下:
(2)++++=++++=0+=.
在图中所示如下:
17. 如图,已知M,N分别为四面体A-BCD的面BCD与面ACD的重心,G为AM上一点,且GM∶GA=1∶3.求证:B,G,N三点共线.
证明 设=a,=b,=c,
则=+=+
=-a+(a+b+c)=-a+b+c,
=+=+(+)=-a+b+c
=,
∴∥.
又BN∩BG=B,∴B,G,N三点共线.
1.1 空间向量及其运算
1.1.1 空间向量及其线性运算
一.选择题
1.下列说法中,错误的是( )
A.向量与的长度相等
B.两个相等的向量,若起点相同,则终点也相同
C.只有零向量的模等于0
D.共线的单位向量都相等
2.下列关于单位向量与零向量的叙述正确的是( )
A.零向量是没有方向的向量,两个单位向量的模相等
B.零向量的方向是任意的,所有单位向量都相等
C.零向量的长度为0,单位向量不一定是相等向量
D.零向量只有一个方向,模相等的单位向量的方向不一定相同
3.(多选)下列说法正确的有( )
A.若A,B,C,D是不共线的四点,则=是四边形ABCD是平行四边形的充要条件
B.若a=b,b=c,则a=c
C.向量a,b相等的充要条件是
D.=的充要条件是A与C重合,B与D重合
4.如图所示空间四边形ABCD,连接AC,BD,设M,G分别是BC,CD的中点,则-+等于( )
A. B.3
C.3 D.2
5.已知正方体ABCD-A1B1C1D1中,=,若=x+y(+),则( )
A.x=1,y= B.x=,y=1
C.x=1,y= D.x=1,y=
6.设空间四点O,A,B,P满足=m+n,其中m+n=1,则( )
A.点P一定在直线AB上
B.点P一定不在直线AB上
C.点P可能在直线AB上,也可能不在直线AB上
D.与的方向一定相同
7.以下说法正确的为( )
A.方向相反的两个向量是相反向量
B.若a,b满足|a|>|b|且a,b同向,则a>b
C.不相等的两个空间向量的模必不相等
D.对于任何向量a,b,必有|a+b|≤|a|+|b|
8.对于空间的任意三个向量a,b,2a-b,它们一定是( )
A.共面向量
B.共线向量
C.不共面向量
D.既不共线也不共面的向量
9.如图,已知平行六面体ABCD-A1B1C1D1,在下列选项中,与相等的向量是( )
A. B.
C. D.
10.在三棱柱ABC-A1B1C1中,D是CC1的中点,F是A1B的中点,且=α+β,则( )
A.α=,β=-1
B.α=-,β=1
C.α=1,β=-
D.α=-1,β=
11.(多选)设A,B,C是空间任意三点,下列结论正确的是( )
A.+= B.++=0
C.-= D.=-
二、填空题
12.在四边形ABCD中,若=+,则四边形ABCD的形状一定是________.
13. 已知M,N分别是四面体OABC的棱OA,BC的中点,点P在线段MN上,且MP=2PN,设向量=a,O=b,O=c,则O=________.
14.如图所示,已知矩形ABCD,P为平面ABCD外一点,且PA⊥平面ABCD,M,N分别为PC,PD上的点,且PM∶MC=2∶1,N为PD的中点,则满足=x+y+z的实数x=________,y=________,z=________.
三、解答题
15.如图所示,已知矩形ABCD和矩形ADEF所在的平面互相垂直,点M,N分别在对角线BD,AE上,且BM=BD,AN=AE.求证:向量,,共面.
16.如图所示,在正六棱柱ABCDEF-A1B1C1D1E1F1中:
(1)化简--+++,并在图中标出化简结果的向量;
(2)化简++++,并在图中标出化简结果的向量.
17. 如图,已知M,N分别为四面体A-BCD的面BCD与面ACD的重心,G为AM上一点,且GM∶GA=1∶3.求证:B,G,N三点共线.
第一章 空间向量与立体几何
1.1 空间向量及其运算
1.1.1 空间向量及其线性运算
一.选择题
1.下列说法中,错误的是( )
A.向量与的长度相等
B.两个相等的向量,若起点相同,则终点也相同
C.只有零向量的模等于0
D.共线的单位向量都相等
答案 D
解析 共线的单位向量是相等向量或相反向量.
2.下列关于单位向量与零向量的叙述正确的是( )
A.零向量是没有方向的向量,两个单位向量的模相等
B.零向量的方向是任意的,所有单位向量都相等
C.零向量的长度为0,单位向量不一定是相等向量
D.零向量只有一个方向,模相等的单位向量的方向不一定相同
答案 C
解析 因为零向量的方向是任意的,且长度为0,两个单位向量的模相等,但方向不一定相同.故选C.
3.(多选)下列说法正确的有( )
A.若A,B,C,D是不共线的四点,则=是四边形ABCD是平行四边形的充要条件
B.若a=b,b=c,则a=c
C.向量a,b相等的充要条件是
D.=的充要条件是A与C重合,B与D重合
答案 AB
解析 A正确,∵=,∴||=||且∥.又A,B,C,D不共线,∴四边形ABCD是平行四边形.反之,在 ABCD中,有=;B正确,∵a=b,∴a,b的长度相等且方向相同.∵b=c,∴b,c的长度相等且方向相同.故a=c;C不正确,由a∥b,知a与b的方向相同或相反;D显然不正确.故选AB.
4.如图所示空间四边形ABCD,连接AC,BD,设M,G分别是BC,CD的中点,则-+等于( )
A. B.3
C.3 D.2
答案 B
解析 -+=-(-)=-=+=+2=3.故选B.
5.已知正方体ABCD-A1B1C1D1中,=,若=x+y(+),则( )
A.x=1,y= B.x=,y=1
C.x=1,y= D.x=1,y=
答案 D
解析 因为=+=+=+(+),所以x=1,y=.
6.设空间四点O,A,B,P满足=m+n,其中m+n=1,则( )
A.点P一定在直线AB上
B.点P一定不在直线AB上
C.点P可能在直线AB上,也可能不在直线AB上
D.与的方向一定相同
答案 A
解析 已知m+n=1,则m=1-n,所以=(1-n)+n=-n+n -=n(-) =n.因为≠0,所以和共线,即点A,P,B共线.故选A.
7.以下说法正确的为( )
A.方向相反的两个向量是相反向量
B.若a,b满足|a|>|b|且a,b同向,则a>b
C.不相等的两个空间向量的模必不相等
D.对于任何向量a,b,必有|a+b|≤|a|+|b|
答案 D
解析 长度相等且方向相反的两个向量是相反向量,故A错误;向量是不能比较大小的,故B错误;不相等的两个空间向量的模也可以相等,故C错误;由向量加法的几何意义可知D正确.故选D.
8.对于空间的任意三个向量a,b,2a-b,它们一定是( )
A.共面向量
B.共线向量
C.不共面向量
D.既不共线也不共面的向量
答案 A
解析 记c=2a-b,由共面向量的判定方法易知,a,b,c三个向量是共面向量.故选A.
9.如图,已知平行六面体ABCD-A1B1C1D1,在下列选项中,与相等的向量是( )
A. B.
C. D.
答案 C
解析 由于ABCD-A1B1C1D1是平行六面体,所以||=||,且与方向相同,故=.故选C.
10.在三棱柱ABC-A1B1C1中,D是CC1的中点,F是A1B的中点,且=α+β,则( )
A.α=,β=-1
B.α=-,β=1
C.α=1,β=-
D.α=-1,β=
答案 A
解析 根据向量加法的多边形法则以及已知可得,=++=++=+-++=-,∴α=,β=-1.故选A.
11.(多选)设A,B,C是空间任意三点,下列结论正确的是( )
A.+= B.++=0
C.-= D.=-
答案 ACD
解析 B中向量的和应该是零向量,而不是数0,B错误;由空间向量的线性运算法则,知A,C,D正确.故选ACD.
二、填空题
12.在四边形ABCD中,若=+,则四边形ABCD的形状一定是________.
答案 平行四边形
解析 因为=+,所以四边形ABCD是以AB与AD为邻边,AC为对角线的平行四边形.
13. 已知M,N分别是四面体OABC的棱OA,BC的中点,点P在线段MN上,且MP=2PN,设向量=a,O=b,O=c,则O=________.
答案 a+b+c
解析 ∵MP=2PN,
∴M=2P,
即O-O=2(O-O),
3O=O+2O=a+b+c,
∴O=a+b+c.
14.如图所示,已知矩形ABCD,P为平面ABCD外一点,且PA⊥平面ABCD,M,N分别为PC,PD上的点,且PM∶MC=2∶1,N为PD的中点,则满足=x+y+z的实数x=________,y=________,z=________.
答案 - -
解析 如图所示,在PD上取一点F,使PF∶FD=2∶1,连接MF,则=+.
∵=-=-==(-),===-,
∴=--+,
∴x=-,y=-,z=.
三、解答题
15.如图所示,已知矩形ABCD和矩形ADEF所在的平面互相垂直,点M,N分别在对角线BD,AE上,且BM=BD,AN=AE.求证:向量,,共面.
证明 因为M在BD上,且BM=BD,
所以==+.
同理=+.
所以=++
=++
=+=+.
又与不共线,根据向量共面的充要条件可知,,共面.
16.如图所示,在正六棱柱ABCDEF-A1B1C1D1E1F1中:
(1)化简--+++,并在图中标出化简结果的向量;
(2)化简++++,并在图中标出化简结果的向量.
解 (1)--+++=+++++=++0=+=.
在图中所示如下:
(2)++++=++++=0+=.
在图中所示如下:
17. 如图,已知M,N分别为四面体A-BCD的面BCD与面ACD的重心,G为AM上一点,且GM∶GA=1∶3.求证:B,G,N三点共线.
证明 设=a,=b,=c,
则=+=+
=-a+(a+b+c)=-a+b+c,
=+=+(+)=-a+b+c
=,
∴∥.
又BN∩BG=B,∴B,G,N三点共线.
