2023-2024学年人教A版数学选择性必修一同步测试1.4.1 用空间向量研究直线、平面的位置关系(含解析)
文档属性
| 名称 | 2023-2024学年人教A版数学选择性必修一同步测试1.4.1 用空间向量研究直线、平面的位置关系(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 414.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 00:00:00 | ||
图片预览




文档简介
第一章 空间向量与立体几何
1.4 空间向量的应用
1.4.1 用空间向量研究直线、平面的位置关系
一.选择题
1.如图所示,已知A,B,C三点不共线,P为平面ABC内一定点,O为平面ABC外任一点,且平面ABC中的小方格为单位正方形,则下列能正确表示向量的为( )
A.+2+2 B.-3-2
C.+3-2 D.+2-3
2.已知=(1,5,-2),=(3,1,z),若⊥,=(x-1,y,-3),且⊥平面ABC,则等于( )
A. B.
C. D.
3.(多选)已知平面α内有一点A(2,-1,2),α的一个法向量为n=,则下列四个点中在平面α内的是( )
A.P1(1,-1,1) B.P2
C.P3 D.P4
4.在正方体ABCD-A1B1C1D1中,若E为A1C1的中点,则直线CE垂直于( )
A.AC B.BD
C.A1D D.A1A
5.已知a=(2,4,5),b=(3,x,y)分别是直线l1,l2的方向向量.若l1∥l2,则( )
A.x=6,y=15 B.x=3,y=
C.x=3,y=15 D.x=6,y=
6.若a=(1,2,3)是平面γ的一个法向量,则下列向量中能作为平面γ的法向量的是( )
A.(0,1,2) B.(3,6,9)
C.(-1,-2,3) D.(3,6,8)
7.若直线l∥α,且l的方向向量为(2,m,1),平面α的法向量为,则m为( )
A.-4 B.-6
C.-8 D.8
8.如图所示,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰三角形,AC=2a,BB1=3a,D是A1C1的中点,点E在棱AA1上,要使CE⊥平面B1DE,则AE=( )
A.a B.2a
C.a或2a D.2a或4a
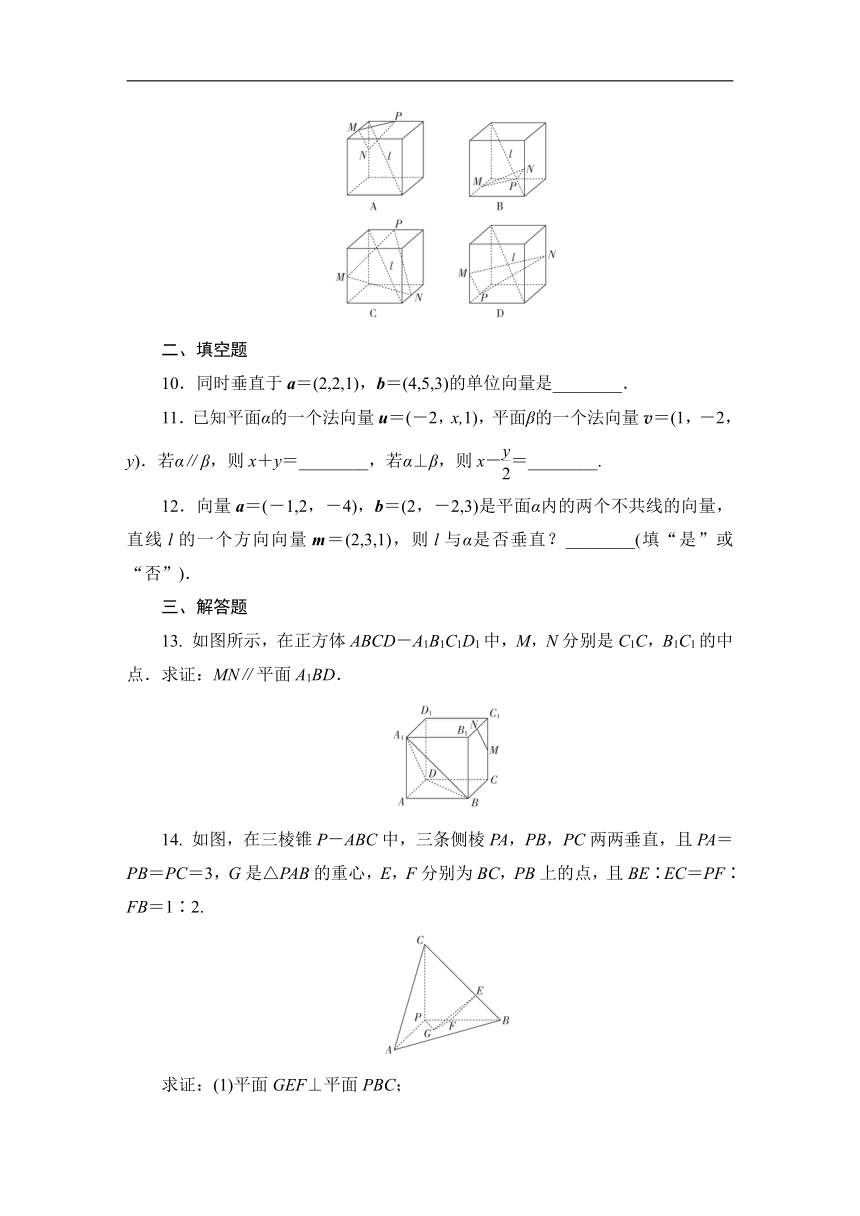
9.(多选)如图所示,在四个正方体中,l是正方体的一条体对角线,点M,N,P分别为其所在棱的中点,能得出l⊥平面MNP的图形为( )
二、填空题
10.同时垂直于a=(2,2,1),b=(4,5,3)的单位向量是________.
11.已知平面α的一个法向量u=(-2,x,1),平面β的一个法向量v=(1,-2,y).若α∥β,则x+y=________,若α⊥β,则x-=________.
12.向量a=(-1,2,-4),b=(2,-2,3)是平面α内的两个不共线的向量,直线l的一个方向向量m=(2,3,1),则l与α是否垂直?________(填“是”或“否”).
三、解答题
13. 如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD.
14. 如图,在三棱锥P-ABC中,三条侧棱PA,PB,PC两两垂直,且PA=PB=PC=3,G是△PAB的重心,E,F分别为BC,PB上的点,且BE∶EC=PF∶FB=1∶2.
求证:(1)平面GEF⊥平面PBC;
(2)EG与直线PG和BC都垂直.
15. 如图,已知P是正方形ABCD所在平面外一点,M,N分别是PA,BD上的点,且PM∶MA=BN∶ND=5∶8.求证:直线MN∥平面PBC.
第一章 空间向量与立体几何
1.4 空间向量的应用
1.4.1 用空间向量研究直线、平面的位置关系
一.选择题
1.如图所示,已知A,B,C三点不共线,P为平面ABC内一定点,O为平面ABC外任一点,且平面ABC中的小方格为单位正方形,则下列能正确表示向量的为( )
A.+2+2 B.-3-2
C.+3-2 D.+2-3
答案 C
解析 连接AP,∵A,B,C,P四点共面,∴可设=x+y,即=+x+y,由题图可知x=3,y=-2.
2.已知=(1,5,-2),=(3,1,z),若⊥,=(x-1,y,-3),且⊥平面ABC,则等于( )
A. B.
C. D.
答案 B
解析 由·=0,得3+5-2z=0,∴z=4.
又⊥平面ABC,∴
即解得
故=.
3.(多选)已知平面α内有一点A(2,-1,2),α的一个法向量为n=,则下列四个点中在平面α内的是( )
A.P1(1,-1,1) B.P2
C.P3 D.P4
答案 BC
解析 对于A中的点P1(1,-1,1),=(1,0,1),·n=≠0,排除A;同理可排除D;对于B中的点P2,=,∴·n=0;对于C中的点P3(2,1,1),=(0,-2,1),∴·n=0.故选BC.
4.在正方体ABCD-A1B1C1D1中,若E为A1C1的中点,则直线CE垂直于( )
A.AC B.BD
C.A1D D.A1A
答案 B
解析 建立如图所示的空间直角坐标系.设正方体的棱长为1,则A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,0),A1(1,0,1),C1(0,1,1),E,∴=,=(-1,1,0),=(-1,-1,0),=(-1,0,-1),=(0,0,-1).∵·=(-1)×+(-1)×+0×1=0,∴CE⊥BD.
5.已知a=(2,4,5),b=(3,x,y)分别是直线l1,l2的方向向量.若l1∥l2,则( )
A.x=6,y=15 B.x=3,y=
C.x=3,y=15 D.x=6,y=
答案 D
解析 因为l1∥l2,所以a∥b,所以== x=6,y=.
6.若a=(1,2,3)是平面γ的一个法向量,则下列向量中能作为平面γ的法向量的是( )
A.(0,1,2) B.(3,6,9)
C.(-1,-2,3) D.(3,6,8)
答案 B
解析 由题意知,与a共线的向量都能作为平面γ的法向量,由(3,6,9)=3(1,2,3)知,向量(3,6,9)与向量a=(1,2,3)共线.故选B.
7.若直线l∥α,且l的方向向量为(2,m,1),平面α的法向量为,则m为( )
A.-4 B.-6
C.-8 D.8
答案 C
解析 ∵l∥α,∴l与平面α的法向量垂直.故2×1+×m+1×2=0,解得m=-8.故选C.
8.如图所示,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰三角形,AC=2a,BB1=3a,D是A1C1的中点,点E在棱AA1上,要使CE⊥平面B1DE,则AE=( )
A.a B.2a
C.a或2a D.2a或4a
答案 C
解析 建立如图所示的空间直角坐标系,则点B1(0,0,3a),C(0,a,0),D.设E(a,0,z)(0≤z≤3a),则=(a,-a,z),=(a,0,z-3a),=.又·=a2-a2+0=0,C·=2a2+z2-3az=0,解得z=a或2a.故AE=a或2a.故选C.
9.(多选)如图所示,在四个正方体中,l是正方体的一条体对角线,点M,N,P分别为其所在棱的中点,能得出l⊥平面MNP的图形为( )
答案 AD
解析 如图所示,正方体ABCD-A′B′C′D′,连接AC,BD,∵M,P分别为其所在棱的中点,∴MP∥AC.∵四边形ABCD为正方形,∴AC⊥BD,
∵BB′⊥平面ABCD,AC 平面ABCD,∴BB′⊥AC,∵AC⊥BD,BD∩BB′=B,∴AC⊥平面DBB′,又DB′ 平面DBB′,∴AC⊥DB′.∵MP∥AC,∴DB′⊥MP,同理,可证DB′⊥NP,∵MP∩NP=P,MP 平面MNP,NP 平面MNP,∴DB′⊥平面MNP,即l⊥平面MNP,故A正确;在D中,与A中证明同理,可证l⊥MP,l⊥MN,又MP∩MN=M,∴l⊥平面MNP,故D正确;对于B,建立空间直角坐标系如图,设正方体的棱长为2,则M(1,0,0),N(2,2,1), =(1,2,1),直线l所在体对角线两个顶点坐标分别为(0,0,2),(2,2,0),
所以直线l的方向向量n=(2,2,-2),∵n·=4≠0,∴直线l不可能垂直于平面MNP,故B错误;同理,可在C中建立相同的空间直角坐标系,则M(2,0,1),N(1,2,0),=(-1,2,-1),∵n·=4≠0,∴直线l不可能垂直于平面MNP,故C错误.故选AD.
二、填空题
10.同时垂直于a=(2,2,1),b=(4,5,3)的单位向量是________.
答案 或
解析 设所求向量为c=(x,y,z),
则解得或
11.已知平面α的一个法向量u=(-2,x,1),平面β的一个法向量v=(1,-2,y).若α∥β,则x+y=________,若α⊥β,则x-=________.
答案 -1
解析 因为α∥β,所以u∥v,所以==,解得x=4,y=-,所以x+y=.因为α⊥β,所以u⊥v,所以-2×1+(-2)x+1×y=0,故x-=-1.
12.向量a=(-1,2,-4),b=(2,-2,3)是平面α内的两个不共线的向量,直线l的一个方向向量m=(2,3,1),则l与α是否垂直?________(填“是”或“否”).
答案 否
解析 m·a=(2,3,1)·(-1,2,-4)=-2+6-4=0,m·b=(2,3,1)·(2,-2,3)=4-6+3=1≠0.所以l与α不垂直.
三、解答题
13. 如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD.
证明 证法一:如图所示,以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
设正方体的棱长为1,则可求得
M,N,D(0,0,0),A1(1,0,1),B(1,1,0),
于是=,=(1,0,1),
=(1,1,0).
设平面A1BD的法向量是n=(x,y,z),
则n·=0,且n·=0,得
取x=1,得y=-1,z=-1,
所以n=(1,-1,-1).
又·n=·(1,-1,-1)=0,
所以⊥n.又MN 平面A1BD,
所以MN∥平面A1BD.
证法二:因为=-=-
=(-)=,
所以∥.
而MN 平面A1BD,DA1 平面A1BD,所以MN∥平面A1BD.
14. 如图,在三棱锥P-ABC中,三条侧棱PA,PB,PC两两垂直,且PA=PB=PC=3,G是△PAB的重心,E,F分别为BC,PB上的点,且BE∶EC=PF∶FB=1∶2.
求证:(1)平面GEF⊥平面PBC;
(2)EG与直线PG和BC都垂直.
证明 (1)如图,以三棱锥的顶点P为原点,PA,PB,PC所在的直线分别为x轴、y轴、z轴建立空间直角坐标系Pxyz.
则A(3,0,0),B(0,3,0),C(0,0,3),E(0,2,1),F(0,1,0),G(1,1,0),P(0,0,0).
于是=(0,-1,-1),
=(1,-1,-1).
设平面GEF的法向量是n=(x,y,z),
则即可取n=(0,1,-1).
显然=(3,0,0)是平面PBC的一个法向量.
又n·=0,∴n⊥,即平面PBC的法向量与平面GEF的法向量垂直,
∴平面GEF⊥平面PBC.
(2)由(1),知=(1,-1,-1),=(1,1,0),=(0,-3,3),
∴·=0,·=0,∴EG⊥PG,EG⊥BC,
∴EG与直线PG和BC都垂直.
15. 如图,已知P是正方形ABCD所在平面外一点,M,N分别是PA,BD上的点,且PM∶MA=BN∶ND=5∶8.求证:直线MN∥平面PBC.
证明 =++
=-++
=-++
=-(-)++(+)
=-+=-,
∴与,共面,
∵MN 平面PBC,∴MN∥平面PBC.
1.4 空间向量的应用
1.4.1 用空间向量研究直线、平面的位置关系
一.选择题
1.如图所示,已知A,B,C三点不共线,P为平面ABC内一定点,O为平面ABC外任一点,且平面ABC中的小方格为单位正方形,则下列能正确表示向量的为( )
A.+2+2 B.-3-2
C.+3-2 D.+2-3
2.已知=(1,5,-2),=(3,1,z),若⊥,=(x-1,y,-3),且⊥平面ABC,则等于( )
A. B.
C. D.
3.(多选)已知平面α内有一点A(2,-1,2),α的一个法向量为n=,则下列四个点中在平面α内的是( )
A.P1(1,-1,1) B.P2
C.P3 D.P4
4.在正方体ABCD-A1B1C1D1中,若E为A1C1的中点,则直线CE垂直于( )
A.AC B.BD
C.A1D D.A1A
5.已知a=(2,4,5),b=(3,x,y)分别是直线l1,l2的方向向量.若l1∥l2,则( )
A.x=6,y=15 B.x=3,y=
C.x=3,y=15 D.x=6,y=
6.若a=(1,2,3)是平面γ的一个法向量,则下列向量中能作为平面γ的法向量的是( )
A.(0,1,2) B.(3,6,9)
C.(-1,-2,3) D.(3,6,8)
7.若直线l∥α,且l的方向向量为(2,m,1),平面α的法向量为,则m为( )
A.-4 B.-6
C.-8 D.8
8.如图所示,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰三角形,AC=2a,BB1=3a,D是A1C1的中点,点E在棱AA1上,要使CE⊥平面B1DE,则AE=( )
A.a B.2a
C.a或2a D.2a或4a
9.(多选)如图所示,在四个正方体中,l是正方体的一条体对角线,点M,N,P分别为其所在棱的中点,能得出l⊥平面MNP的图形为( )
二、填空题
10.同时垂直于a=(2,2,1),b=(4,5,3)的单位向量是________.
11.已知平面α的一个法向量u=(-2,x,1),平面β的一个法向量v=(1,-2,y).若α∥β,则x+y=________,若α⊥β,则x-=________.
12.向量a=(-1,2,-4),b=(2,-2,3)是平面α内的两个不共线的向量,直线l的一个方向向量m=(2,3,1),则l与α是否垂直?________(填“是”或“否”).
三、解答题
13. 如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD.
14. 如图,在三棱锥P-ABC中,三条侧棱PA,PB,PC两两垂直,且PA=PB=PC=3,G是△PAB的重心,E,F分别为BC,PB上的点,且BE∶EC=PF∶FB=1∶2.
求证:(1)平面GEF⊥平面PBC;
(2)EG与直线PG和BC都垂直.
15. 如图,已知P是正方形ABCD所在平面外一点,M,N分别是PA,BD上的点,且PM∶MA=BN∶ND=5∶8.求证:直线MN∥平面PBC.
第一章 空间向量与立体几何
1.4 空间向量的应用
1.4.1 用空间向量研究直线、平面的位置关系
一.选择题
1.如图所示,已知A,B,C三点不共线,P为平面ABC内一定点,O为平面ABC外任一点,且平面ABC中的小方格为单位正方形,则下列能正确表示向量的为( )
A.+2+2 B.-3-2
C.+3-2 D.+2-3
答案 C
解析 连接AP,∵A,B,C,P四点共面,∴可设=x+y,即=+x+y,由题图可知x=3,y=-2.
2.已知=(1,5,-2),=(3,1,z),若⊥,=(x-1,y,-3),且⊥平面ABC,则等于( )
A. B.
C. D.
答案 B
解析 由·=0,得3+5-2z=0,∴z=4.
又⊥平面ABC,∴
即解得
故=.
3.(多选)已知平面α内有一点A(2,-1,2),α的一个法向量为n=,则下列四个点中在平面α内的是( )
A.P1(1,-1,1) B.P2
C.P3 D.P4
答案 BC
解析 对于A中的点P1(1,-1,1),=(1,0,1),·n=≠0,排除A;同理可排除D;对于B中的点P2,=,∴·n=0;对于C中的点P3(2,1,1),=(0,-2,1),∴·n=0.故选BC.
4.在正方体ABCD-A1B1C1D1中,若E为A1C1的中点,则直线CE垂直于( )
A.AC B.BD
C.A1D D.A1A
答案 B
解析 建立如图所示的空间直角坐标系.设正方体的棱长为1,则A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,0),A1(1,0,1),C1(0,1,1),E,∴=,=(-1,1,0),=(-1,-1,0),=(-1,0,-1),=(0,0,-1).∵·=(-1)×+(-1)×+0×1=0,∴CE⊥BD.
5.已知a=(2,4,5),b=(3,x,y)分别是直线l1,l2的方向向量.若l1∥l2,则( )
A.x=6,y=15 B.x=3,y=
C.x=3,y=15 D.x=6,y=
答案 D
解析 因为l1∥l2,所以a∥b,所以== x=6,y=.
6.若a=(1,2,3)是平面γ的一个法向量,则下列向量中能作为平面γ的法向量的是( )
A.(0,1,2) B.(3,6,9)
C.(-1,-2,3) D.(3,6,8)
答案 B
解析 由题意知,与a共线的向量都能作为平面γ的法向量,由(3,6,9)=3(1,2,3)知,向量(3,6,9)与向量a=(1,2,3)共线.故选B.
7.若直线l∥α,且l的方向向量为(2,m,1),平面α的法向量为,则m为( )
A.-4 B.-6
C.-8 D.8
答案 C
解析 ∵l∥α,∴l与平面α的法向量垂直.故2×1+×m+1×2=0,解得m=-8.故选C.
8.如图所示,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰三角形,AC=2a,BB1=3a,D是A1C1的中点,点E在棱AA1上,要使CE⊥平面B1DE,则AE=( )
A.a B.2a
C.a或2a D.2a或4a
答案 C
解析 建立如图所示的空间直角坐标系,则点B1(0,0,3a),C(0,a,0),D.设E(a,0,z)(0≤z≤3a),则=(a,-a,z),=(a,0,z-3a),=.又·=a2-a2+0=0,C·=2a2+z2-3az=0,解得z=a或2a.故AE=a或2a.故选C.
9.(多选)如图所示,在四个正方体中,l是正方体的一条体对角线,点M,N,P分别为其所在棱的中点,能得出l⊥平面MNP的图形为( )
答案 AD
解析 如图所示,正方体ABCD-A′B′C′D′,连接AC,BD,∵M,P分别为其所在棱的中点,∴MP∥AC.∵四边形ABCD为正方形,∴AC⊥BD,
∵BB′⊥平面ABCD,AC 平面ABCD,∴BB′⊥AC,∵AC⊥BD,BD∩BB′=B,∴AC⊥平面DBB′,又DB′ 平面DBB′,∴AC⊥DB′.∵MP∥AC,∴DB′⊥MP,同理,可证DB′⊥NP,∵MP∩NP=P,MP 平面MNP,NP 平面MNP,∴DB′⊥平面MNP,即l⊥平面MNP,故A正确;在D中,与A中证明同理,可证l⊥MP,l⊥MN,又MP∩MN=M,∴l⊥平面MNP,故D正确;对于B,建立空间直角坐标系如图,设正方体的棱长为2,则M(1,0,0),N(2,2,1), =(1,2,1),直线l所在体对角线两个顶点坐标分别为(0,0,2),(2,2,0),
所以直线l的方向向量n=(2,2,-2),∵n·=4≠0,∴直线l不可能垂直于平面MNP,故B错误;同理,可在C中建立相同的空间直角坐标系,则M(2,0,1),N(1,2,0),=(-1,2,-1),∵n·=4≠0,∴直线l不可能垂直于平面MNP,故C错误.故选AD.
二、填空题
10.同时垂直于a=(2,2,1),b=(4,5,3)的单位向量是________.
答案 或
解析 设所求向量为c=(x,y,z),
则解得或
11.已知平面α的一个法向量u=(-2,x,1),平面β的一个法向量v=(1,-2,y).若α∥β,则x+y=________,若α⊥β,则x-=________.
答案 -1
解析 因为α∥β,所以u∥v,所以==,解得x=4,y=-,所以x+y=.因为α⊥β,所以u⊥v,所以-2×1+(-2)x+1×y=0,故x-=-1.
12.向量a=(-1,2,-4),b=(2,-2,3)是平面α内的两个不共线的向量,直线l的一个方向向量m=(2,3,1),则l与α是否垂直?________(填“是”或“否”).
答案 否
解析 m·a=(2,3,1)·(-1,2,-4)=-2+6-4=0,m·b=(2,3,1)·(2,-2,3)=4-6+3=1≠0.所以l与α不垂直.
三、解答题
13. 如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是C1C,B1C1的中点.求证:MN∥平面A1BD.
证明 证法一:如图所示,以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
设正方体的棱长为1,则可求得
M,N,D(0,0,0),A1(1,0,1),B(1,1,0),
于是=,=(1,0,1),
=(1,1,0).
设平面A1BD的法向量是n=(x,y,z),
则n·=0,且n·=0,得
取x=1,得y=-1,z=-1,
所以n=(1,-1,-1).
又·n=·(1,-1,-1)=0,
所以⊥n.又MN 平面A1BD,
所以MN∥平面A1BD.
证法二:因为=-=-
=(-)=,
所以∥.
而MN 平面A1BD,DA1 平面A1BD,所以MN∥平面A1BD.
14. 如图,在三棱锥P-ABC中,三条侧棱PA,PB,PC两两垂直,且PA=PB=PC=3,G是△PAB的重心,E,F分别为BC,PB上的点,且BE∶EC=PF∶FB=1∶2.
求证:(1)平面GEF⊥平面PBC;
(2)EG与直线PG和BC都垂直.
证明 (1)如图,以三棱锥的顶点P为原点,PA,PB,PC所在的直线分别为x轴、y轴、z轴建立空间直角坐标系Pxyz.
则A(3,0,0),B(0,3,0),C(0,0,3),E(0,2,1),F(0,1,0),G(1,1,0),P(0,0,0).
于是=(0,-1,-1),
=(1,-1,-1).
设平面GEF的法向量是n=(x,y,z),
则即可取n=(0,1,-1).
显然=(3,0,0)是平面PBC的一个法向量.
又n·=0,∴n⊥,即平面PBC的法向量与平面GEF的法向量垂直,
∴平面GEF⊥平面PBC.
(2)由(1),知=(1,-1,-1),=(1,1,0),=(0,-3,3),
∴·=0,·=0,∴EG⊥PG,EG⊥BC,
∴EG与直线PG和BC都垂直.
15. 如图,已知P是正方形ABCD所在平面外一点,M,N分别是PA,BD上的点,且PM∶MA=BN∶ND=5∶8.求证:直线MN∥平面PBC.
证明 =++
=-++
=-++
=-(-)++(+)
=-+=-,
∴与,共面,
∵MN 平面PBC,∴MN∥平面PBC.
