2023-2024学年人教A版数学选择性必修一同步测试第一章空间向量与立体几何(含答案)
文档属性
| 名称 | 2023-2024学年人教A版数学选择性必修一同步测试第一章空间向量与立体几何(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 551.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 00:00:00 | ||
图片预览




文档简介
第一章空间向量与立体几何
时间:120分钟 满分:150分
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知空间三点O(0,0,0),A(-1,1,0),B(0,1,1),在直线OA上有一点H满足BH⊥OA,则点H的坐标为( )
A.(-2,2,0) B.(2,-2,0)
C. D.
2.已知向量a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),则下列结论正确的是( )
A.a∥c,b∥c B.a∥b,a⊥c
C.a∥c,a⊥b D.a∥b,b⊥c
3.已知A(1,0,0),B(0,1,0),C(0,0,1),则平面ABC的一个法向量是( )
A.(1,1,-1) B.(1,-1,1)
C.(-1,1,1) D.(-1,-1,-1)
4.已知a=3m-2n-4p≠0,b=(x+1)m+8n+2yp,且m,n,p不共面,若a∥b,则x,y的值为( )
A.x=-13,y=8 B.x=-13,y=5
C.x=7,y=5 D.x=7,y=8
5.已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).若|a|=,且a分别与,垂直,则向量a为( )
A.(1,1,1)
B.(-1,-1,-1)或(1,1,1)
C.(-1,-1,-1)
D.(1,-1,1)或(-1,1,-1)
6.如图,正方形ABCD与矩形ACEF所在平面互相垂直,AB=,AF=1,M在EF上,且AM∥平面BDE,则M点的坐标为( )
A.(1,1,1) B.
C. D.
7.在三棱锥P-ABC中,△ABC为等边三角形,PA⊥平面ABC,且PA=AB,则平面PBC与平面PAB夹角的正切值为( )
A. B.
C. D.
8.如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )
A. B.
C. D.2
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.若A,B,C,D为空间不同的四点,则下列各式为零向量的是( )
A.+2+2+
B.2+2+3+3+
C.++
D.-+-
10.设向量i,j,k是不共面的三个向量,则下列各组向量能作为空间向量基底的是( )
A.p=i-2j+k,q=-i+3j+2k,r=-3i+7j
B.p=i+j-k,q=2i+3j-5k,r=-7i+18j+22k
C.p=i+j,q=i+k,r=j+k
D.p=i+j,q=i-j,r=k
11.定义空间两个非零向量的一种运算a b=|a||b|sin〈a,b〉,则关于空间向量上述运算的以下结论中恒成立的有( )
A.a b=b a
B.λ(a b)=(λa) b
C.(a+b) c=(a c)+(b c)
D.若a=(x1,y1,0),b=(x2,y2,0),则a b=|x1y2-x2y1|
12.如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,M是棱AA1的中点,点P在侧面ABB1A1内.下列结论正确的是( )
A.直线CM与平面ABCD所成角的余弦值为
B.||的最大值为2
C.cos∠A1D1P的取值范围为
D.若D1P⊥CM,则△PBC的面积的最小值为
三、填空题(本题共4小题,每小题5分,共20分)
13.已知a=(3λ,6,λ+6),b=(λ+1,3,2λ)为两平行平面的法向量,则λ=________.
14.若A(x,5-x,2x-1),B(1,x+2,2-x),则当||取最小值时,x的值等于________.
15.如图,在空间四边形ABCD中,AC和BD为对角线,G为△ABC的重心,E是BD上一点,BE=3ED,以{,,}为基底,则=________.
16.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是棱CC1上的一点,CP=m,若直线AP与平面BDD1B1所成角的正弦值为,则m=________,此时异面直线AP与A1B1所成角的余弦值为________.
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)已知向量a=(1,-3,2),b=(-2,1,1),点A(-3,-1,4),B(-2,-2,2).
(1)求|2a+b|;
(2)在直线AB上是否存在一点E,使得⊥b(O为坐标原点)
18.(本小题满分12分) 如图所示,底面ABCD是正方形,AS⊥平面ABCD,且AS=AB,E是SC的中点.求证:平面BDE⊥平面ABCD.
19.(本小题满分12分)如图所示,平行六面体ABCD-A1B1C1D1中,E,F分别在B1B和D1D上,且BE=BB1,DF=DD1.
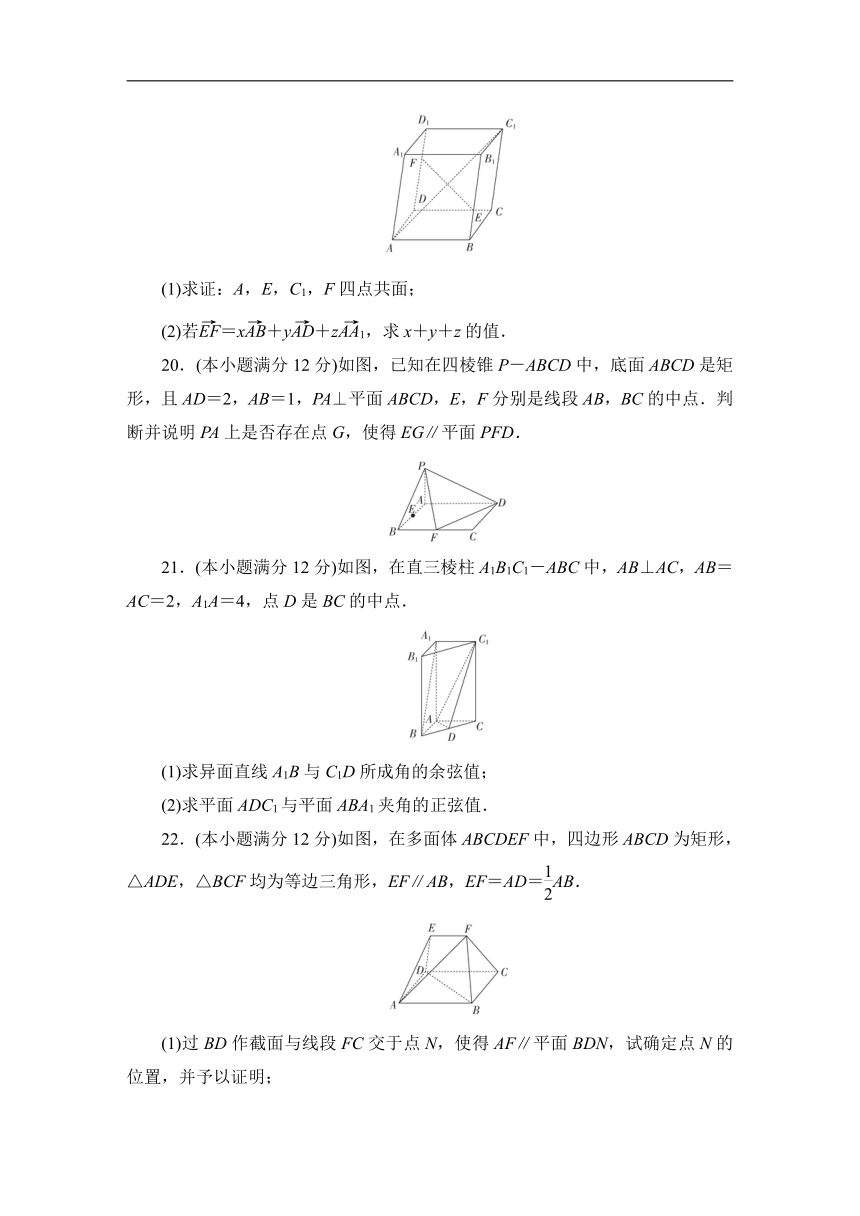
(1)求证:A,E,C1,F四点共面;
(2)若=x+y+z,求x+y+z的值.
20.(本小题满分12分)如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.判断并说明PA上是否存在点G,使得EG∥平面PFD.
21.(本小题满分12分)如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.
(1)求异面直线A1B与C1D所成角的余弦值;
(2)求平面ADC1与平面ABA1夹角的正弦值.
22.(本小题满分12分)如图,在多面体ABCDEF中,四边形ABCD为矩形,△ADE,△BCF均为等边三角形,EF∥AB,EF=AD=AB.
(1)过BD作截面与线段FC交于点N,使得AF∥平面BDN,试确定点N的位置,并予以证明;
(2)在(1)的条件下,求直线BN与平面ABF所成角的正弦值.
第一章空间向量与立体几何
时间:120分钟 满分:150分
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知空间三点O(0,0,0),A(-1,1,0),B(0,1,1),在直线OA上有一点H满足BH⊥OA,则点H的坐标为( )
A.(-2,2,0) B.(2,-2,0)
C. D.
答案 C
解析 由=(-1,1,0),且点H在直线OA上,可设H(-λ,λ,0),则=(-λ,λ-1,-1).又BH⊥OA,∴·=0,即(-λ,λ-1,-1)·(-1,1,0)=0,即λ+λ-1=0,解得λ=,∴H.故选C.
2.已知向量a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),则下列结论正确的是( )
A.a∥c,b∥c B.a∥b,a⊥c
C.a∥c,a⊥b D.a∥b,b⊥c
答案 C
解析 ∵a=(-2,-3,1),c=(-4,-6,2),∴c=2a,∴a∥c.又a·b=(-2,-3,1)·(2,0,4)=0,∴a⊥b.故选C.
3.已知A(1,0,0),B(0,1,0),C(0,0,1),则平面ABC的一个法向量是( )
A.(1,1,-1) B.(1,-1,1)
C.(-1,1,1) D.(-1,-1,-1)
答案 D
解析 =(-1,1,0),=(-1,0,1).设平面ABC的法向量为n=(x,y,z),则有取x=-1,则y=-1,z=-1.故平面ABC的一个法向量是(-1,-1,-1).故选D.
4.已知a=3m-2n-4p≠0,b=(x+1)m+8n+2yp,且m,n,p不共面,若a∥b,则x,y的值为( )
A.x=-13,y=8 B.x=-13,y=5
C.x=7,y=5 D.x=7,y=8
答案 A
解析 ∵a∥b且a≠0,∴b=λa,即(x+1)m+8n+2yp=3λm-2λn-4λp.又m,n,p不共面,∴==,∴x=-13,y=8.故选A.
5.已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).若|a|=,且a分别与,垂直,则向量a为( )
A.(1,1,1)
B.(-1,-1,-1)或(1,1,1)
C.(-1,-1,-1)
D.(1,-1,1)或(-1,1,-1)
答案 B
解析 设a=(x,y,z),因为=(-2,-1,3),=(1,-3,2),则解得a=(1,1,1)或(-1,-1,-1).
6.如图,正方形ABCD与矩形ACEF所在平面互相垂直,AB=,AF=1,M在EF上,且AM∥平面BDE,则M点的坐标为( )
A.(1,1,1) B.
C. D.
答案 C
解析 设M点的坐标为(x,y,1),因为AC∩BD=O,所以O,又E(0,0,1),A(,,0),所以=, =(x-,y-,1),因为AM∥平面BDE,所以∥,所以==,解得所以M点的坐标为.故选C.
7.在三棱锥P-ABC中,△ABC为等边三角形,PA⊥平面ABC,且PA=AB,则平面PBC与平面PAB夹角的正切值为( )
A. B.
C. D.
答案 A
解析 设PA=AB=2,建立如图所示的空间直角坐标系,则B(0,2,0),C(,1,0),P(0,0,2),∴=(0,-2,2),=(,-1,0).设n=(x,y,z)是平面PBC的法向量,则即令y=1,则x=,z=1,即n=.易知m=(1,0,0)是平面PAB的一个法向量,则|cos〈m,n〉|===.
∴tan〈m,n〉=.故选A.
8.如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )
A. B.
C. D.2
答案 B
解析 如图,作EO⊥AB于O,以OE所在直线为x轴,O为坐标原点,过O作平行于AD的直线为z轴,建立如图所示的空间直角坐标系,
则A(0,-1,0),E(1,0,0),D(0,-1,2),C(0,1,2).则=(0,0,2),=(1,1,0),=(0,2,2).设平面ACE的法向量n=(x,y,z),则即令y=1,∴n=(-1,1,-1).故点D到平面ACE的距离d===.故选B.
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.若A,B,C,D为空间不同的四点,则下列各式为零向量的是( )
A.+2+2+
B.2+2+3+3+
C.++
D.-+-
答案 BD
解析 A中,原式=+2+=+++=+,不符合题意;B中,原式=2(+++)+(++)=0;C中,原式=,不符合题意;D中,原式=(-)+(-)=0.故选BD.
10.设向量i,j,k是不共面的三个向量,则下列各组向量能作为空间向量基底的是( )
A.p=i-2j+k,q=-i+3j+2k,r=-3i+7j
B.p=i+j-k,q=2i+3j-5k,r=-7i+18j+22k
C.p=i+j,q=i+k,r=j+k
D.p=i+j,q=i-j,r=k
答案 BCD
解析 对于A,令r=mp+nq,则-3i+7j=m(i-2j+k)+n(-i+3j+2k)=(m-n)i+(3n-2m)j+(m+2n)k,故得m=-2,n=1,即r=-2p+q,也就是说向量p,q,r共面,从而不能作为空间向量的一个基底.同理可得其他选项对应的三个向量不共面,即可作为空间向量的一个基底.故选BCD.
11.定义空间两个非零向量的一种运算a b=|a||b|sin〈a,b〉,则关于空间向量上述运算的以下结论中恒成立的有( )
A.a b=b a
B.λ(a b)=(λa) b
C.(a+b) c=(a c)+(b c)
D.若a=(x1,y1,0),b=(x2,y2,0),则a b=|x1y2-x2y1|
答案 AD
解析 对于A,a b=|a||b|sin〈a,b〉,b a=|b||a|·sin〈b,a〉,故a b=b a恒成立;对于B,λ(a b)=λ(|a||b|sin〈a,b〉),(λa) b=|λ||a||b|sin〈λa,b〉,故λ(a b)=(λa) b不会恒成立;对于C,令a=λb,则(a+b) c=|1+λ||b||c|sin〈(1+λ)b,c〉,(a c)+(b c)=|λb||c|sin〈λb,c〉+|b||c|sin〈b,c〉.若λ≥0,等式成立;若λ<0,等式显然不成立.故(a+b) c=(a c)+(b c)不会恒成立;对于D,cos〈a,b〉=,
sin〈a,b〉=,
则有a b=|a||b|·
=|a|·
=·
=
==|x1y2-x2y1|.
则a b=|x1y2-x2y1|恒成立.故选AD.
12.如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,M是棱AA1的中点,点P在侧面ABB1A1内.下列结论正确的是( )
A.直线CM与平面ABCD所成角的余弦值为
B.||的最大值为2
C.cos∠A1D1P的取值范围为
D.若D1P⊥CM,则△PBC的面积的最小值为
答案 ABCD
解析 对于A,连接AC,易知∠MCA即为直线CM与平面ABCD所成的角,AC=2,CM=3,则cos∠MCA=,A正确;对于B,以A为坐标原点,AB,AD,AA1所在的直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则D1(0,2,2).
∵点P在侧面ABB1A1内,∴设P(a,0,b),a,b∈[0,2],则=(a,-2,b-2),∴||=∈[2,2],即||的最大值为2,B正确;对于C,cos∠A1D1P==∈,C正确;对于D,∵M(0,0,1),C(2,2,0),B(2,0,0),C=(-2,-2,1),P=(2-a,0,-b),D1P⊥CM,∴·=-2a+4+b-2=0,即b=2a-2,∴a∈[1,2].∵BC⊥平面ABB1A1,∴BC⊥PB,∴S△PBC=BC·PB=×2×PB= .将b=2a-2代入,可得S△PBC==,a∈[1,2],∴当a=时,S△PBC取得最小值,最小值为,D正确.故选ABCD.
三、填空题(本题共4小题,每小题5分,共20分)
13.已知a=(3λ,6,λ+6),b=(λ+1,3,2λ)为两平行平面的法向量,则λ=________.
答案 2
解析 由题意知a∥b,所以==,解得λ=2.
14.若A(x,5-x,2x-1),B(1,x+2,2-x),则当||取最小值时,x的值等于________.
答案
解析 =(1-x,2x-3,-3x+3),
则||=
==,
故当x=时,||取最小值.
15.如图,在空间四边形ABCD中,AC和BD为对角线,G为△ABC的重心,E是BD上一点,BE=3ED,以{,,}为基底,则=________.
答案 --+
解析 连接AE,则=-=+-
=+-(+)
=+---
=--+.
16.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是棱CC1上的一点,CP=m,若直线AP与平面BDD1B1所成角的正弦值为,则m=________,此时异面直线AP与A1B1所成角的余弦值为________.
答案
解析 如图,连接AC,以D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系Dxyz,则A(1,0,0),P(0,1,m),C(0,1,0),D(0,0,0),所以=(-1,1,m),=(-1,1,0),
又·=0,·=0,
所以是平面BDD1B1的一个法向量.
设AP与平面BDD1B1所成的角为θ,
则sinθ=|cos〈,〉|===,所以m=.
异面直线AP与A1B1所成角,即为AP与AB所成角,即∠PAB,由m=,得AP==,则cos∠PAB==,即异面直线AP与A1B1所成角的余弦值为.
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)已知向量a=(1,-3,2),b=(-2,1,1),点A(-3,-1,4),B(-2,-2,2).
(1)求|2a+b|;
(2)在直线AB上是否存在一点E,使得⊥b(O为坐标原点)
解 (1)因为a=(1,-3,2),b=(-2,1,1),所以2a+b=(0,-5,5),所以|2a+b|==5.
(2)假设存在点E,设其坐标为E(x,y,z),
则=λ,即(x+3,y+1,z-4)=λ(1,-1,-2),
所以
所以E(λ-3,-λ-1,-2λ+4),
所以=(λ-3,-λ-1,-2λ+4).
又因为b=(-2,1,1),⊥b,
所以·b=-2(λ-3)+(-λ-1)+(-2λ+4)=-5λ+9=0,
所以λ=,所以E,
所以在直线AB上存在点E,
使得⊥B.
18.(本小题满分12分) 如图所示,底面ABCD是正方形,AS⊥平面ABCD,且AS=AB,E是SC的中点.求证:平面BDE⊥平面ABCD.
证明 设AB=BC=CD=DA=AS=1,建立如图所示的空间直角坐标系,则A(0,0,0),B(1,0,0),D(0,1,0),S(0,0,1),E.
证法一:连接AC,设AC与BD相交于点O,连接OE,则点O的坐标为.
因为=(0,0,1),=,
所以=,所以OE∥AS.
又AS⊥平面ABCD,所以OE⊥平面ABCD.
又OE 平面BDE,所以平面BDE⊥平面ABCD.
证法二:设平面BDE的法向量为n1=(x,y,z),
因为=(-1,1,0),=,
所以即
令x=1,可得平面BDE的一个法向量n1=(1,1,0).
因为AS⊥平面ABCD,
所以平面ABCD的一个法向量n2==(0,0,1),
因为n1·n2=0,所以平面BDE⊥平面ABCD.
19.(本小题满分12分)如图所示,平行六面体ABCD-A1B1C1D1中,E,F分别在B1B和D1D上,且BE=BB1,DF=DD1.
(1)求证:A,E,C1,F四点共面;
(2)若=x+y+z,求x+y+z的值.
解 (1)证明:因为=++
=+++
=+
=(+)+(+)
=+,
所以A,E,C1,F四点共面.
(2)因为=-=+-(+)
=+--
=-++,
所以x=-1,y=1,z=,
所以x+y+z=.
20.(本小题满分12分)如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.判断并说明PA上是否存在点G,使得EG∥平面PFD.
解 ∵PA⊥平面ABCD,
∠BAD=90°,AB=1,AD=2,
如图,建立空间直角坐标系Axyz,
则A(0,0,0),B(1,0,0),F(1,1,0),D(0,2,0).
不妨令P(0,0,t),
∴=(1,1,-t),=(1,-1,0),
设平面PFD的法向量为n=(x,y,z),
由得
令z=1,解得x=y=,∴n=.
设点G的坐标为(0,0,m),
又E,则=.
要使EG∥平面PFD,只需·n=0,
即×+0×+m×1=0,即m-=0,
解得m=t,从而满足AG=AP的点G即为所求.
21.(本小题满分12分)如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.
(1)求异面直线A1B与C1D所成角的余弦值;
(2)求平面ADC1与平面ABA1夹角的正弦值.
解 (1)以A为坐标原点,建立如图所示的空间直角坐标系Axyz,
则A(0,0,0),B(2,0,0),C(0,2,0),D(1,1,0),A1(0,0,4),C1(0,2,4).
所以=(2,0,-4),=(1,-1,-4).
所以cos〈,〉=
==,
所以异面直线A1B与C1D所成角的余弦值为.
(2)设平面ADC1的法向量为n1=(x,y,z),
因为=(1,1,0),=(0,2,4),
所以n1·=0,n1·=0,
即x+y=0且y+2z=0.取z=1,得x=2,y=-2,
所以n1=(2,-2,1)是平面ADC1的一个法向量.
取平面ABA1的一个法向量为n2=(0,1,0),
设平面ADC1与平面ABA1的夹角为θ.
由cosθ===,得sinθ=.
因此,平面ADC1与平面ABA1夹角的正弦值为.
22.(本小题满分12分)如图,在多面体ABCDEF中,四边形ABCD为矩形,△ADE,△BCF均为等边三角形,EF∥AB,EF=AD=AB.
(1)过BD作截面与线段FC交于点N,使得AF∥平面BDN,试确定点N的位置,并予以证明;
(2)在(1)的条件下,求直线BN与平面ABF所成角的正弦值.
解 (1)当N为线段FC的中点时,AF∥平面BDN.
证明如下:如图所示,连接AC,且AC与BD的交点为O,连接ON.
∵四边形ABCD为矩形,
∴O为AC的中点.
又N为FC的中点,∴AF∥ON.
∵AF 平面BDN,ON 平面BDN,
∴AF∥平面BDN.
故当N为FC的中点时,AF∥平面BDN.
(2)过O作PQ∥AB分别与AD,BC交于P,Q.
∵O为AC的中点,
∴P,Q分别为AD,BC的中点.
∵△ADE与△BCF均为等边三角形且AD=BC,
∴△ADE≌△BCF.连接EP,FQ,则EP=FQ.
∵EF∥AB,AB綊PQ,EF=AB,
∴EF∥PQ,EF=PQ,
∴四边形EPQF为等腰梯形.
取EF的中点M,连接MO,则MO⊥PQ.
又AD⊥EP,AD⊥PQ,EP∩PQ=P,
∴AD⊥平面EPQF.过点O作OG⊥AB于点G,则OG∥AD,
∴OG⊥平面EPQF,∴OG⊥OM,OG⊥OQ.
分别以,,的方向为x轴、y轴、z轴的正方向,建立如图所示的空间直角坐标系Oxyz,
不妨设AB=4,则由条件可得
O(0,0,0),A(1,-2,0),B(1,2,0),F(0,1,),D(-1,-2,0),N,则=(0,4,0),=(-1,3,).
设n=(x,y,z)是平面ABF的法向量,则
即
∴可取n=(,0,1).
由=,
可得|cos〈,n〉|==,
∴直线BN与平面ABF所成角的正弦值为.
时间:120分钟 满分:150分
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知空间三点O(0,0,0),A(-1,1,0),B(0,1,1),在直线OA上有一点H满足BH⊥OA,则点H的坐标为( )
A.(-2,2,0) B.(2,-2,0)
C. D.
2.已知向量a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),则下列结论正确的是( )
A.a∥c,b∥c B.a∥b,a⊥c
C.a∥c,a⊥b D.a∥b,b⊥c
3.已知A(1,0,0),B(0,1,0),C(0,0,1),则平面ABC的一个法向量是( )
A.(1,1,-1) B.(1,-1,1)
C.(-1,1,1) D.(-1,-1,-1)
4.已知a=3m-2n-4p≠0,b=(x+1)m+8n+2yp,且m,n,p不共面,若a∥b,则x,y的值为( )
A.x=-13,y=8 B.x=-13,y=5
C.x=7,y=5 D.x=7,y=8
5.已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).若|a|=,且a分别与,垂直,则向量a为( )
A.(1,1,1)
B.(-1,-1,-1)或(1,1,1)
C.(-1,-1,-1)
D.(1,-1,1)或(-1,1,-1)
6.如图,正方形ABCD与矩形ACEF所在平面互相垂直,AB=,AF=1,M在EF上,且AM∥平面BDE,则M点的坐标为( )
A.(1,1,1) B.
C. D.
7.在三棱锥P-ABC中,△ABC为等边三角形,PA⊥平面ABC,且PA=AB,则平面PBC与平面PAB夹角的正切值为( )
A. B.
C. D.
8.如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )
A. B.
C. D.2
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.若A,B,C,D为空间不同的四点,则下列各式为零向量的是( )
A.+2+2+
B.2+2+3+3+
C.++
D.-+-
10.设向量i,j,k是不共面的三个向量,则下列各组向量能作为空间向量基底的是( )
A.p=i-2j+k,q=-i+3j+2k,r=-3i+7j
B.p=i+j-k,q=2i+3j-5k,r=-7i+18j+22k
C.p=i+j,q=i+k,r=j+k
D.p=i+j,q=i-j,r=k
11.定义空间两个非零向量的一种运算a b=|a||b|sin〈a,b〉,则关于空间向量上述运算的以下结论中恒成立的有( )
A.a b=b a
B.λ(a b)=(λa) b
C.(a+b) c=(a c)+(b c)
D.若a=(x1,y1,0),b=(x2,y2,0),则a b=|x1y2-x2y1|
12.如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,M是棱AA1的中点,点P在侧面ABB1A1内.下列结论正确的是( )
A.直线CM与平面ABCD所成角的余弦值为
B.||的最大值为2
C.cos∠A1D1P的取值范围为
D.若D1P⊥CM,则△PBC的面积的最小值为
三、填空题(本题共4小题,每小题5分,共20分)
13.已知a=(3λ,6,λ+6),b=(λ+1,3,2λ)为两平行平面的法向量,则λ=________.
14.若A(x,5-x,2x-1),B(1,x+2,2-x),则当||取最小值时,x的值等于________.
15.如图,在空间四边形ABCD中,AC和BD为对角线,G为△ABC的重心,E是BD上一点,BE=3ED,以{,,}为基底,则=________.
16.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是棱CC1上的一点,CP=m,若直线AP与平面BDD1B1所成角的正弦值为,则m=________,此时异面直线AP与A1B1所成角的余弦值为________.
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)已知向量a=(1,-3,2),b=(-2,1,1),点A(-3,-1,4),B(-2,-2,2).
(1)求|2a+b|;
(2)在直线AB上是否存在一点E,使得⊥b(O为坐标原点)
18.(本小题满分12分) 如图所示,底面ABCD是正方形,AS⊥平面ABCD,且AS=AB,E是SC的中点.求证:平面BDE⊥平面ABCD.
19.(本小题满分12分)如图所示,平行六面体ABCD-A1B1C1D1中,E,F分别在B1B和D1D上,且BE=BB1,DF=DD1.
(1)求证:A,E,C1,F四点共面;
(2)若=x+y+z,求x+y+z的值.
20.(本小题满分12分)如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.判断并说明PA上是否存在点G,使得EG∥平面PFD.
21.(本小题满分12分)如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.
(1)求异面直线A1B与C1D所成角的余弦值;
(2)求平面ADC1与平面ABA1夹角的正弦值.
22.(本小题满分12分)如图,在多面体ABCDEF中,四边形ABCD为矩形,△ADE,△BCF均为等边三角形,EF∥AB,EF=AD=AB.
(1)过BD作截面与线段FC交于点N,使得AF∥平面BDN,试确定点N的位置,并予以证明;
(2)在(1)的条件下,求直线BN与平面ABF所成角的正弦值.
第一章空间向量与立体几何
时间:120分钟 满分:150分
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知空间三点O(0,0,0),A(-1,1,0),B(0,1,1),在直线OA上有一点H满足BH⊥OA,则点H的坐标为( )
A.(-2,2,0) B.(2,-2,0)
C. D.
答案 C
解析 由=(-1,1,0),且点H在直线OA上,可设H(-λ,λ,0),则=(-λ,λ-1,-1).又BH⊥OA,∴·=0,即(-λ,λ-1,-1)·(-1,1,0)=0,即λ+λ-1=0,解得λ=,∴H.故选C.
2.已知向量a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),则下列结论正确的是( )
A.a∥c,b∥c B.a∥b,a⊥c
C.a∥c,a⊥b D.a∥b,b⊥c
答案 C
解析 ∵a=(-2,-3,1),c=(-4,-6,2),∴c=2a,∴a∥c.又a·b=(-2,-3,1)·(2,0,4)=0,∴a⊥b.故选C.
3.已知A(1,0,0),B(0,1,0),C(0,0,1),则平面ABC的一个法向量是( )
A.(1,1,-1) B.(1,-1,1)
C.(-1,1,1) D.(-1,-1,-1)
答案 D
解析 =(-1,1,0),=(-1,0,1).设平面ABC的法向量为n=(x,y,z),则有取x=-1,则y=-1,z=-1.故平面ABC的一个法向量是(-1,-1,-1).故选D.
4.已知a=3m-2n-4p≠0,b=(x+1)m+8n+2yp,且m,n,p不共面,若a∥b,则x,y的值为( )
A.x=-13,y=8 B.x=-13,y=5
C.x=7,y=5 D.x=7,y=8
答案 A
解析 ∵a∥b且a≠0,∴b=λa,即(x+1)m+8n+2yp=3λm-2λn-4λp.又m,n,p不共面,∴==,∴x=-13,y=8.故选A.
5.已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).若|a|=,且a分别与,垂直,则向量a为( )
A.(1,1,1)
B.(-1,-1,-1)或(1,1,1)
C.(-1,-1,-1)
D.(1,-1,1)或(-1,1,-1)
答案 B
解析 设a=(x,y,z),因为=(-2,-1,3),=(1,-3,2),则解得a=(1,1,1)或(-1,-1,-1).
6.如图,正方形ABCD与矩形ACEF所在平面互相垂直,AB=,AF=1,M在EF上,且AM∥平面BDE,则M点的坐标为( )
A.(1,1,1) B.
C. D.
答案 C
解析 设M点的坐标为(x,y,1),因为AC∩BD=O,所以O,又E(0,0,1),A(,,0),所以=, =(x-,y-,1),因为AM∥平面BDE,所以∥,所以==,解得所以M点的坐标为.故选C.
7.在三棱锥P-ABC中,△ABC为等边三角形,PA⊥平面ABC,且PA=AB,则平面PBC与平面PAB夹角的正切值为( )
A. B.
C. D.
答案 A
解析 设PA=AB=2,建立如图所示的空间直角坐标系,则B(0,2,0),C(,1,0),P(0,0,2),∴=(0,-2,2),=(,-1,0).设n=(x,y,z)是平面PBC的法向量,则即令y=1,则x=,z=1,即n=.易知m=(1,0,0)是平面PAB的一个法向量,则|cos〈m,n〉|===.
∴tan〈m,n〉=.故选A.
8.如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )
A. B.
C. D.2
答案 B
解析 如图,作EO⊥AB于O,以OE所在直线为x轴,O为坐标原点,过O作平行于AD的直线为z轴,建立如图所示的空间直角坐标系,
则A(0,-1,0),E(1,0,0),D(0,-1,2),C(0,1,2).则=(0,0,2),=(1,1,0),=(0,2,2).设平面ACE的法向量n=(x,y,z),则即令y=1,∴n=(-1,1,-1).故点D到平面ACE的距离d===.故选B.
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.若A,B,C,D为空间不同的四点,则下列各式为零向量的是( )
A.+2+2+
B.2+2+3+3+
C.++
D.-+-
答案 BD
解析 A中,原式=+2+=+++=+,不符合题意;B中,原式=2(+++)+(++)=0;C中,原式=,不符合题意;D中,原式=(-)+(-)=0.故选BD.
10.设向量i,j,k是不共面的三个向量,则下列各组向量能作为空间向量基底的是( )
A.p=i-2j+k,q=-i+3j+2k,r=-3i+7j
B.p=i+j-k,q=2i+3j-5k,r=-7i+18j+22k
C.p=i+j,q=i+k,r=j+k
D.p=i+j,q=i-j,r=k
答案 BCD
解析 对于A,令r=mp+nq,则-3i+7j=m(i-2j+k)+n(-i+3j+2k)=(m-n)i+(3n-2m)j+(m+2n)k,故得m=-2,n=1,即r=-2p+q,也就是说向量p,q,r共面,从而不能作为空间向量的一个基底.同理可得其他选项对应的三个向量不共面,即可作为空间向量的一个基底.故选BCD.
11.定义空间两个非零向量的一种运算a b=|a||b|sin〈a,b〉,则关于空间向量上述运算的以下结论中恒成立的有( )
A.a b=b a
B.λ(a b)=(λa) b
C.(a+b) c=(a c)+(b c)
D.若a=(x1,y1,0),b=(x2,y2,0),则a b=|x1y2-x2y1|
答案 AD
解析 对于A,a b=|a||b|sin〈a,b〉,b a=|b||a|·sin〈b,a〉,故a b=b a恒成立;对于B,λ(a b)=λ(|a||b|sin〈a,b〉),(λa) b=|λ||a||b|sin〈λa,b〉,故λ(a b)=(λa) b不会恒成立;对于C,令a=λb,则(a+b) c=|1+λ||b||c|sin〈(1+λ)b,c〉,(a c)+(b c)=|λb||c|sin〈λb,c〉+|b||c|sin〈b,c〉.若λ≥0,等式成立;若λ<0,等式显然不成立.故(a+b) c=(a c)+(b c)不会恒成立;对于D,cos〈a,b〉=,
sin〈a,b〉=,
则有a b=|a||b|·
=|a|·
=·
=
==|x1y2-x2y1|.
则a b=|x1y2-x2y1|恒成立.故选AD.
12.如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,M是棱AA1的中点,点P在侧面ABB1A1内.下列结论正确的是( )
A.直线CM与平面ABCD所成角的余弦值为
B.||的最大值为2
C.cos∠A1D1P的取值范围为
D.若D1P⊥CM,则△PBC的面积的最小值为
答案 ABCD
解析 对于A,连接AC,易知∠MCA即为直线CM与平面ABCD所成的角,AC=2,CM=3,则cos∠MCA=,A正确;对于B,以A为坐标原点,AB,AD,AA1所在的直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则D1(0,2,2).
∵点P在侧面ABB1A1内,∴设P(a,0,b),a,b∈[0,2],则=(a,-2,b-2),∴||=∈[2,2],即||的最大值为2,B正确;对于C,cos∠A1D1P==∈,C正确;对于D,∵M(0,0,1),C(2,2,0),B(2,0,0),C=(-2,-2,1),P=(2-a,0,-b),D1P⊥CM,∴·=-2a+4+b-2=0,即b=2a-2,∴a∈[1,2].∵BC⊥平面ABB1A1,∴BC⊥PB,∴S△PBC=BC·PB=×2×PB= .将b=2a-2代入,可得S△PBC==,a∈[1,2],∴当a=时,S△PBC取得最小值,最小值为,D正确.故选ABCD.
三、填空题(本题共4小题,每小题5分,共20分)
13.已知a=(3λ,6,λ+6),b=(λ+1,3,2λ)为两平行平面的法向量,则λ=________.
答案 2
解析 由题意知a∥b,所以==,解得λ=2.
14.若A(x,5-x,2x-1),B(1,x+2,2-x),则当||取最小值时,x的值等于________.
答案
解析 =(1-x,2x-3,-3x+3),
则||=
==,
故当x=时,||取最小值.
15.如图,在空间四边形ABCD中,AC和BD为对角线,G为△ABC的重心,E是BD上一点,BE=3ED,以{,,}为基底,则=________.
答案 --+
解析 连接AE,则=-=+-
=+-(+)
=+---
=--+.
16.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,P是棱CC1上的一点,CP=m,若直线AP与平面BDD1B1所成角的正弦值为,则m=________,此时异面直线AP与A1B1所成角的余弦值为________.
答案
解析 如图,连接AC,以D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系Dxyz,则A(1,0,0),P(0,1,m),C(0,1,0),D(0,0,0),所以=(-1,1,m),=(-1,1,0),
又·=0,·=0,
所以是平面BDD1B1的一个法向量.
设AP与平面BDD1B1所成的角为θ,
则sinθ=|cos〈,〉|===,所以m=.
异面直线AP与A1B1所成角,即为AP与AB所成角,即∠PAB,由m=,得AP==,则cos∠PAB==,即异面直线AP与A1B1所成角的余弦值为.
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)已知向量a=(1,-3,2),b=(-2,1,1),点A(-3,-1,4),B(-2,-2,2).
(1)求|2a+b|;
(2)在直线AB上是否存在一点E,使得⊥b(O为坐标原点)
解 (1)因为a=(1,-3,2),b=(-2,1,1),所以2a+b=(0,-5,5),所以|2a+b|==5.
(2)假设存在点E,设其坐标为E(x,y,z),
则=λ,即(x+3,y+1,z-4)=λ(1,-1,-2),
所以
所以E(λ-3,-λ-1,-2λ+4),
所以=(λ-3,-λ-1,-2λ+4).
又因为b=(-2,1,1),⊥b,
所以·b=-2(λ-3)+(-λ-1)+(-2λ+4)=-5λ+9=0,
所以λ=,所以E,
所以在直线AB上存在点E,
使得⊥B.
18.(本小题满分12分) 如图所示,底面ABCD是正方形,AS⊥平面ABCD,且AS=AB,E是SC的中点.求证:平面BDE⊥平面ABCD.
证明 设AB=BC=CD=DA=AS=1,建立如图所示的空间直角坐标系,则A(0,0,0),B(1,0,0),D(0,1,0),S(0,0,1),E.
证法一:连接AC,设AC与BD相交于点O,连接OE,则点O的坐标为.
因为=(0,0,1),=,
所以=,所以OE∥AS.
又AS⊥平面ABCD,所以OE⊥平面ABCD.
又OE 平面BDE,所以平面BDE⊥平面ABCD.
证法二:设平面BDE的法向量为n1=(x,y,z),
因为=(-1,1,0),=,
所以即
令x=1,可得平面BDE的一个法向量n1=(1,1,0).
因为AS⊥平面ABCD,
所以平面ABCD的一个法向量n2==(0,0,1),
因为n1·n2=0,所以平面BDE⊥平面ABCD.
19.(本小题满分12分)如图所示,平行六面体ABCD-A1B1C1D1中,E,F分别在B1B和D1D上,且BE=BB1,DF=DD1.
(1)求证:A,E,C1,F四点共面;
(2)若=x+y+z,求x+y+z的值.
解 (1)证明:因为=++
=+++
=+
=(+)+(+)
=+,
所以A,E,C1,F四点共面.
(2)因为=-=+-(+)
=+--
=-++,
所以x=-1,y=1,z=,
所以x+y+z=.
20.(本小题满分12分)如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.判断并说明PA上是否存在点G,使得EG∥平面PFD.
解 ∵PA⊥平面ABCD,
∠BAD=90°,AB=1,AD=2,
如图,建立空间直角坐标系Axyz,
则A(0,0,0),B(1,0,0),F(1,1,0),D(0,2,0).
不妨令P(0,0,t),
∴=(1,1,-t),=(1,-1,0),
设平面PFD的法向量为n=(x,y,z),
由得
令z=1,解得x=y=,∴n=.
设点G的坐标为(0,0,m),
又E,则=.
要使EG∥平面PFD,只需·n=0,
即×+0×+m×1=0,即m-=0,
解得m=t,从而满足AG=AP的点G即为所求.
21.(本小题满分12分)如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.
(1)求异面直线A1B与C1D所成角的余弦值;
(2)求平面ADC1与平面ABA1夹角的正弦值.
解 (1)以A为坐标原点,建立如图所示的空间直角坐标系Axyz,
则A(0,0,0),B(2,0,0),C(0,2,0),D(1,1,0),A1(0,0,4),C1(0,2,4).
所以=(2,0,-4),=(1,-1,-4).
所以cos〈,〉=
==,
所以异面直线A1B与C1D所成角的余弦值为.
(2)设平面ADC1的法向量为n1=(x,y,z),
因为=(1,1,0),=(0,2,4),
所以n1·=0,n1·=0,
即x+y=0且y+2z=0.取z=1,得x=2,y=-2,
所以n1=(2,-2,1)是平面ADC1的一个法向量.
取平面ABA1的一个法向量为n2=(0,1,0),
设平面ADC1与平面ABA1的夹角为θ.
由cosθ===,得sinθ=.
因此,平面ADC1与平面ABA1夹角的正弦值为.
22.(本小题满分12分)如图,在多面体ABCDEF中,四边形ABCD为矩形,△ADE,△BCF均为等边三角形,EF∥AB,EF=AD=AB.
(1)过BD作截面与线段FC交于点N,使得AF∥平面BDN,试确定点N的位置,并予以证明;
(2)在(1)的条件下,求直线BN与平面ABF所成角的正弦值.
解 (1)当N为线段FC的中点时,AF∥平面BDN.
证明如下:如图所示,连接AC,且AC与BD的交点为O,连接ON.
∵四边形ABCD为矩形,
∴O为AC的中点.
又N为FC的中点,∴AF∥ON.
∵AF 平面BDN,ON 平面BDN,
∴AF∥平面BDN.
故当N为FC的中点时,AF∥平面BDN.
(2)过O作PQ∥AB分别与AD,BC交于P,Q.
∵O为AC的中点,
∴P,Q分别为AD,BC的中点.
∵△ADE与△BCF均为等边三角形且AD=BC,
∴△ADE≌△BCF.连接EP,FQ,则EP=FQ.
∵EF∥AB,AB綊PQ,EF=AB,
∴EF∥PQ,EF=PQ,
∴四边形EPQF为等腰梯形.
取EF的中点M,连接MO,则MO⊥PQ.
又AD⊥EP,AD⊥PQ,EP∩PQ=P,
∴AD⊥平面EPQF.过点O作OG⊥AB于点G,则OG∥AD,
∴OG⊥平面EPQF,∴OG⊥OM,OG⊥OQ.
分别以,,的方向为x轴、y轴、z轴的正方向,建立如图所示的空间直角坐标系Oxyz,
不妨设AB=4,则由条件可得
O(0,0,0),A(1,-2,0),B(1,2,0),F(0,1,),D(-1,-2,0),N,则=(0,4,0),=(-1,3,).
设n=(x,y,z)是平面ABF的法向量,则
即
∴可取n=(,0,1).
由=,
可得|cos〈,n〉|==,
∴直线BN与平面ABF所成角的正弦值为.
