1.2一定是直角三角形吗课件

课件22张PPT。第一章 勾股定理1.2 一定是直角三角形吗复习旧知勾股定理： 直角三角形两直角边的平方和等于斜边的
平方，如果用a，b和c分别表示直角三角形的两
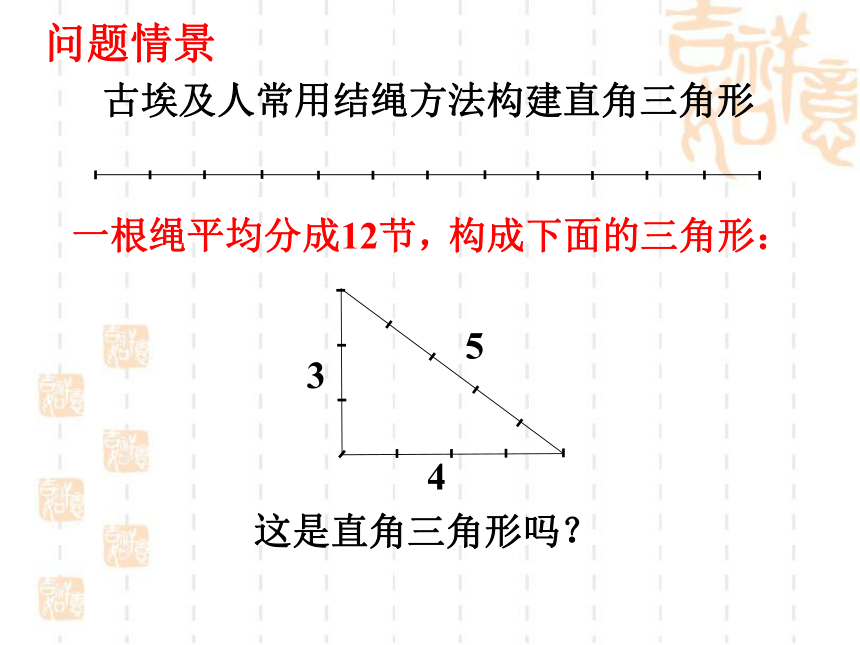
直角边和斜边，那么a2+b2=c2。ABCabc 古埃及人常用结绳方法构建直角三角形 一根绳平均分成12节， 构成下面的三角形： 这是直角三角形吗？问题情景 3 4 5情景引入如果a2+b2=c2，那么这个三角形是直角三角形吗？ABCabc 用a，b，c分别表示三角形的三边合作交流 下面的每组数分别是一个三角形的三边长a，b，c，而且都满足a2+b2=c2 ：① 3，4，5② 5，12，13③ 8，15，17 分别以每组数为三边作出三角形，用量角器
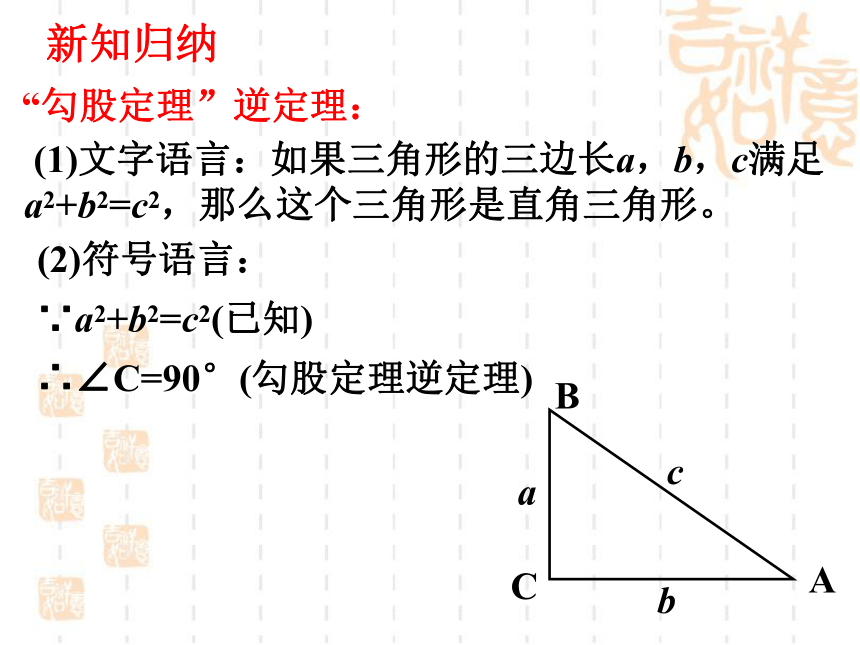
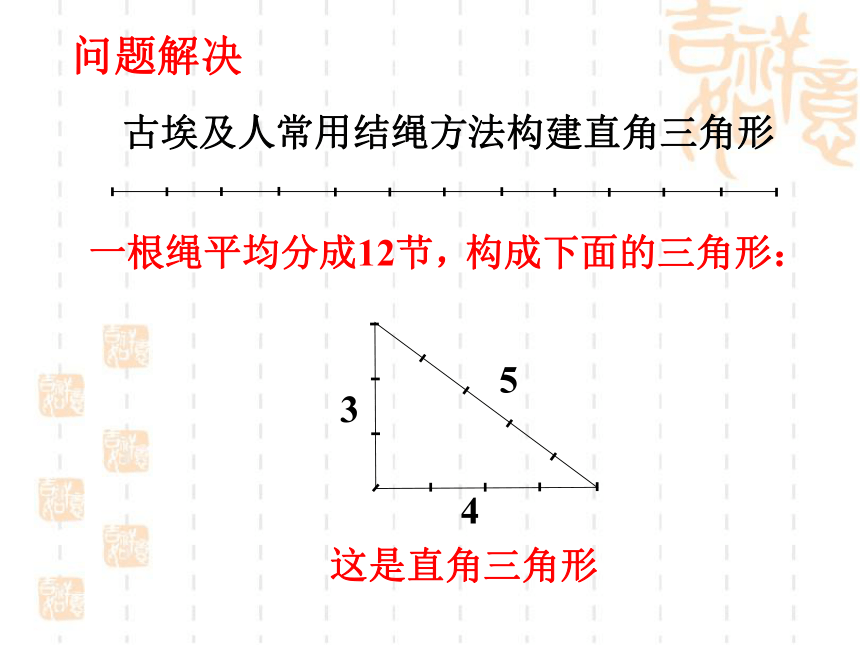
量一量，你有什么发现？9+16=2525+144=16964+225=289新知探究已知：在△ABC中，三边长分别为a，b，c，且a2+b2=c2，你能否判断△ABC是直角三角形？并说明理由。ABCabcMC`Naba2+b2=c2=AB2A`B`2= a2+b2∴△ABC≌△A`B`C`∴∠C=90°新知归纳“勾股定理”逆定理： (1)文字语言：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形。ABCabc∵a2+b2=c2(已知) (2)符号语言：∴∠C=90°(勾股定理逆定理)问题解决 这是直角三角形 3 4 5 古埃及人常用结绳方法构建直角三角形 一根绳平均分成12节， 构成下面的三角形：巩固练习1、如果三条线段a，b，c满足a2=c2- b2，这三条
线段组成的三角形是直角三角形吗？为什么？新知归纳“勾股定理”逆定理的应用： 已知三边特殊关系，判定直角三角形。范例讲解例1、一个零件的形状如图(1)所示，按规定这个
零件中∠A和∠DBC都应为直角，工人师傅量得
这个零件各边尺寸如图(2)所示，这个零件合格吗？图(1)图(2)巩固练习2、如图，在正方形ABCD中，AB=4，AE=2，
DF=1，图中有几个直角三角形，你是如何判断
的？与你的同伴交流。422134BE2=42+22=20FE2=12+22=5FB2=32+42=25BE2+FE2=FB2巩固练习3、如图，哪些是直角三角形，哪些不是，说说
你的理由？拓广探索 下列几组数据能否作为直角三角形的三边？
(1) 9，12，15; (2) 15，36，39;
(3) 12，35，36 ; (4) 12，18，22。(1) 92+122=152 能作为直角三角形的三边(2) 152+362=392 能作为直角三角形的三边(3) 122+352≠362 不能作为直角三角形的三边(4) 122+182≠222 不能作为直角三角形的三边拓广探索92+122=152 以上两组数有什么特点？152+362=392 1、都是正整数；(1) 9，12，15; (2) 15，36，39;2、都满足a2+b2=c2。新知归纳“勾股数”的定义：满足a2+b2=c2的三个正整数，称为勾股数。巩固练习4、(1)如果将直角三角形的三边长同时扩大一个相同的倍数，得到的三角形还是直角三角形吗？巩固练习4、(2)下表中第一列每组数都是勾股数，补全下表，这些数的2倍、3倍、4倍、10倍还是勾股数吗？任意倍呢？说说你的理由。拓展阅读巩固练习5、给你一个长绳子，没有其他工具，你能方便
地得到一个直角吗？课堂小结“勾股定理”逆定理： (1)文字语言：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形。ABCabc∵a2+b2=c2(已知) (2)符号语言：∴∠C=90°(勾股定理逆定理)课堂小结“勾股定理”逆定理的应用： 已知三边特殊关系，判定直角三角形。“勾股数”的定义：满足a2+b2=c2的三个正整数，称为勾股数。