数学人教A版(2019)选择性必修第一册2.2.3直线的一般式方程(共22张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.2.3直线的一般式方程(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
2.2.3直线的一般式方程
复习导入
直线方程
点斜式 × √ √
斜截式 × √ √
两点式 × × √
截距式 × × ×
【答案】(1);(2)=1;
(3); (4).
新知探究
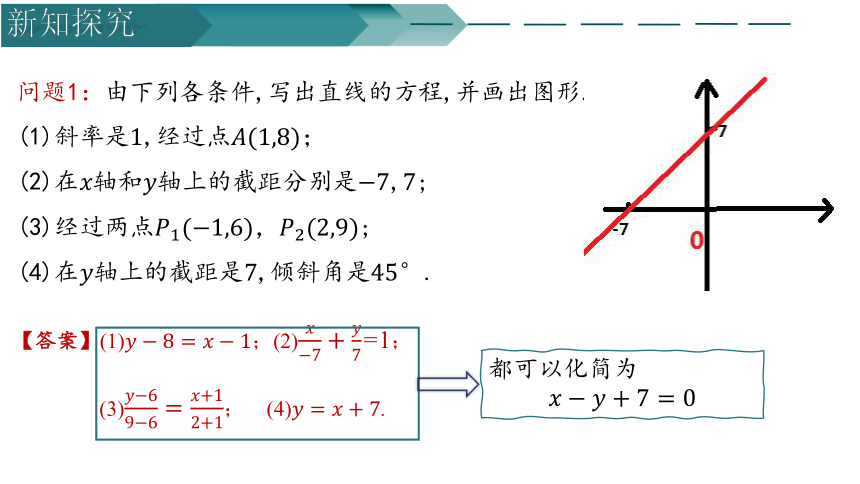
问题1:由下列各条件,写出直线的方程,并画出图形.
(1)斜率是,经过点;
(2)在轴和轴上的截距分别是,;
(3)经过两点,;
(4)在轴上的截距是,倾斜角是.
都可以化简为
新知探究
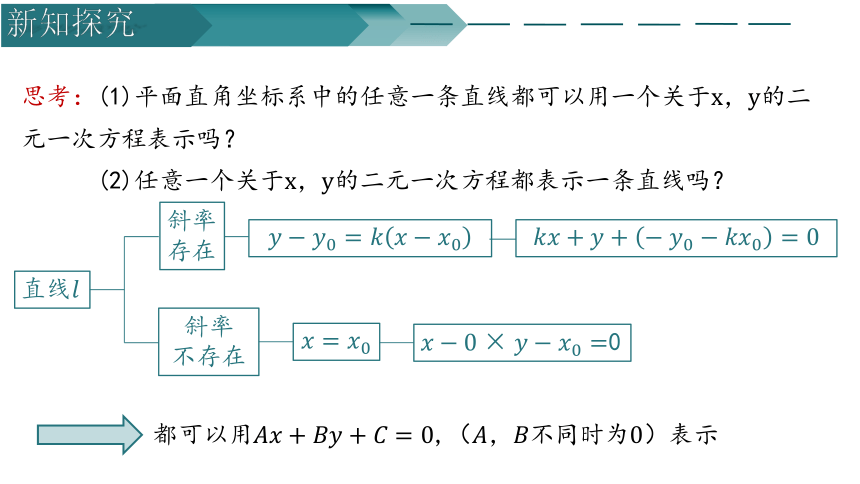
思考:(1)平面直角坐标系中的任意一条直线都可以用一个关于,的二元一次方程表示吗?
(2)任意一个关于的二元一次方程都表示一条直线吗?
直线
斜率存在
斜率
不存在
0
都可以用,(,不同时为)表示
新知探究
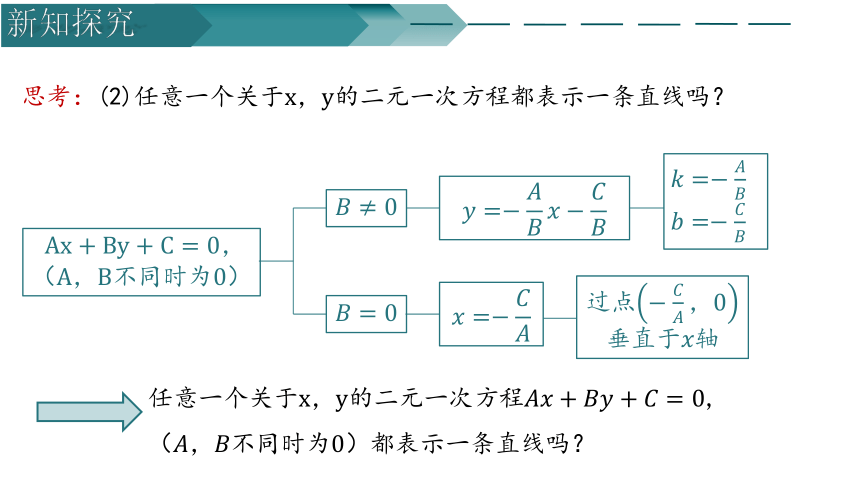
思考:(2)任意一个关于的二元一次方程都表示一条直线吗?
(,不同时为)
过点
垂直于轴
任意一个关于的二元一次方程,(,不同时为)都表示一条直线吗?
新知探究
我们把关于的二元一次方程
(其中,不同时为0)叫做直线的一般式方程,简称一般式.
注:直线的一般式适用于所有直线.
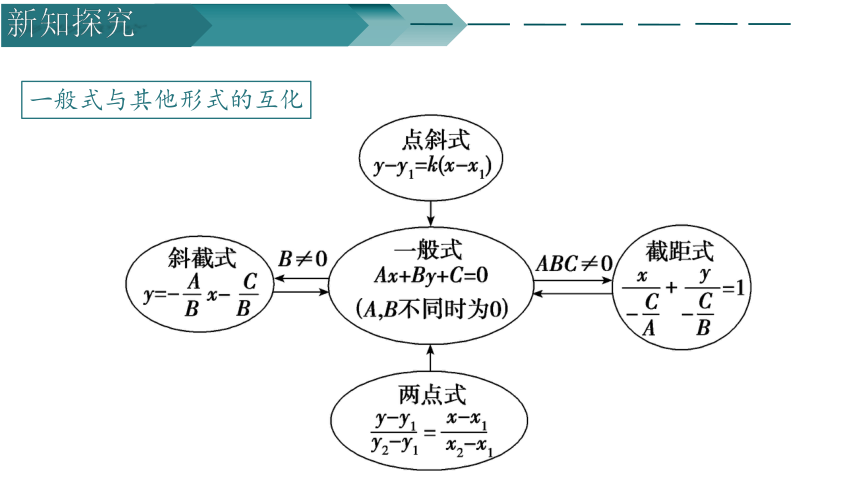
问题2:你能试着互化直线的一般式与我们前面所学的直线的其他形式吗?
新知探究
一般式与其他形式的互化
练习巩固
练习1:斜率为,且在轴上截距为的直线的一般式方程是( ).
、 、 、 、
【答案】
变式1-1:在直角坐标系中,直线的倾斜角是( ).
、 、 、 、
【答案】
新知探究
问题3:在方程中,为何值时,方程表示的直线:
①平行于轴?②平行于轴?③与轴重合?④与轴重合?
①此时,
②此时不存在,
③,此时
④,此时不存在,
练习巩固
例5:已知直线过点,斜率为,求直线的点斜式和一般式方程.
解:经过点,斜率为的直线的
点斜式方程是,
化为一般式,得.
练习巩固
例6:把直线的一般式方程化为斜截式,求出直线的斜率以及它在轴与轴上的截距,并画出图形.
解:把直线的一般式方程化为斜截式.
因此,直线的斜率,它在轴上的截距是.
在直线的方程中,令,得,
即直线在轴上的截距是.
由上面可得直线与轴、轴的交点分别为,,
过,两点作直线,就得直线(如图).
练习巩固
练习2:根据下列条件分别写出直线的方程,并化为一般式方程:
(1)斜率是,且经过点;
(2)斜率是,在轴上的截距为;
解:(1)由点斜式,得直线方程为,
即.
(2)由斜截式,得直线方程为,
即.
练习巩固
练习2:根据下列条件分别写出直线的方程,并化为一般式方程:
(3)经过点两,点;
(4)在轴,轴上的截距分别为,;
(5)经过点,且平行于轴.
解: (3)由两点式,得直线方程为,
即.
(4)由截距式,得直线方程为,
即.
(5).
练习巩固
变式2:已知直线经过点,,求直线的点斜式、斜截式和一般式方程,并根据方程指出直线在轴、轴上的截距.
解: ∵,所以点斜式方程为,
斜截式方程为,
一般式方程为,
直线在轴上的截距为,在轴上的截距为.
练习巩固
练习3:(1)已知直线与直线平行,求的值;
解: (1)由,知:
①当时,显然与不平行;
②当时,,需.
解得或,
∴的值为或.
练习巩固
练习3:(2)当为何值时,直线与直线互相垂直?
解: (2)由题意知,直线.
①若1,即时,直线与直线显然垂直.
②若1即时,直线与直线不垂直.
③若1且,则直线,的斜率都存在,
,.当时,即解得综上可知,当或时,直线.
新知探究
两条直线的位置关系
练习巩固
变式3:已知直线的方程为求满足下列条件的直线的方程.
(1)过点,且与平行;
(2)过点,且与垂直.
解: (1)由与平行,可设的方程为.
将点代入上式得.
∴所求直线的方程为.
(2)由与垂直,可设的方程为.
将点代入上式得.
∴所求直线的方程为.
练习巩固
练习4:已知直线.
(1)求证:不论为何值,直线总经过第一象限;
解: (1)证明:将直线的方程整理为,
∴直线的斜率为,且过定点,
而点在第一象限内,故不论为何值,恒过第一象限.
练习巩固
练习4:已知直线.
(2)为使直线不经过第二象限,求的取值范围.
解: 直线的斜率为.
如图所示,要使不经过第二象限,需斜率,
∴,即的取值范围为.
练习巩固
变式4:已知直线.若直线不经过第二象限,求的取值范围.
解:①当,即时,直线方程为,该直线不经过第二象限,
满足要求.
②当,即时,直线化为截距式方程,
因为直线不过第二象限,故该直线的斜率大于等于零,且在轴的截距小于等于零,即解得所以.
由①②可得,的取值范围为.
小结
形式 方程 适用条件
点斜式 斜率存在的直线
斜截式 斜率存在的直线
两点式 斜率存在且不为
截距式 斜率存在且不为,不过原点
一般式 (,不同时为) 所有
2.2.3直线的一般式方程
复习导入
直线方程
点斜式 × √ √
斜截式 × √ √
两点式 × × √
截距式 × × ×
【答案】(1);(2)=1;
(3); (4).
新知探究
问题1:由下列各条件,写出直线的方程,并画出图形.
(1)斜率是,经过点;
(2)在轴和轴上的截距分别是,;
(3)经过两点,;
(4)在轴上的截距是,倾斜角是.
都可以化简为
新知探究
思考:(1)平面直角坐标系中的任意一条直线都可以用一个关于,的二元一次方程表示吗?
(2)任意一个关于的二元一次方程都表示一条直线吗?
直线
斜率存在
斜率
不存在
0
都可以用,(,不同时为)表示
新知探究
思考:(2)任意一个关于的二元一次方程都表示一条直线吗?
(,不同时为)
过点
垂直于轴
任意一个关于的二元一次方程,(,不同时为)都表示一条直线吗?
新知探究
我们把关于的二元一次方程
(其中,不同时为0)叫做直线的一般式方程,简称一般式.
注:直线的一般式适用于所有直线.
问题2:你能试着互化直线的一般式与我们前面所学的直线的其他形式吗?
新知探究
一般式与其他形式的互化
练习巩固
练习1:斜率为,且在轴上截距为的直线的一般式方程是( ).
、 、 、 、
【答案】
变式1-1:在直角坐标系中,直线的倾斜角是( ).
、 、 、 、
【答案】
新知探究
问题3:在方程中,为何值时,方程表示的直线:
①平行于轴?②平行于轴?③与轴重合?④与轴重合?
①此时,
②此时不存在,
③,此时
④,此时不存在,
练习巩固
例5:已知直线过点,斜率为,求直线的点斜式和一般式方程.
解:经过点,斜率为的直线的
点斜式方程是,
化为一般式,得.
练习巩固
例6:把直线的一般式方程化为斜截式,求出直线的斜率以及它在轴与轴上的截距,并画出图形.
解:把直线的一般式方程化为斜截式.
因此,直线的斜率,它在轴上的截距是.
在直线的方程中,令,得,
即直线在轴上的截距是.
由上面可得直线与轴、轴的交点分别为,,
过,两点作直线,就得直线(如图).
练习巩固
练习2:根据下列条件分别写出直线的方程,并化为一般式方程:
(1)斜率是,且经过点;
(2)斜率是,在轴上的截距为;
解:(1)由点斜式,得直线方程为,
即.
(2)由斜截式,得直线方程为,
即.
练习巩固
练习2:根据下列条件分别写出直线的方程,并化为一般式方程:
(3)经过点两,点;
(4)在轴,轴上的截距分别为,;
(5)经过点,且平行于轴.
解: (3)由两点式,得直线方程为,
即.
(4)由截距式,得直线方程为,
即.
(5).
练习巩固
变式2:已知直线经过点,,求直线的点斜式、斜截式和一般式方程,并根据方程指出直线在轴、轴上的截距.
解: ∵,所以点斜式方程为,
斜截式方程为,
一般式方程为,
直线在轴上的截距为,在轴上的截距为.
练习巩固
练习3:(1)已知直线与直线平行,求的值;
解: (1)由,知:
①当时,显然与不平行;
②当时,,需.
解得或,
∴的值为或.
练习巩固
练习3:(2)当为何值时,直线与直线互相垂直?
解: (2)由题意知,直线.
①若1,即时,直线与直线显然垂直.
②若1即时,直线与直线不垂直.
③若1且,则直线,的斜率都存在,
,.当时,即解得综上可知,当或时,直线.
新知探究
两条直线的位置关系
练习巩固
变式3:已知直线的方程为求满足下列条件的直线的方程.
(1)过点,且与平行;
(2)过点,且与垂直.
解: (1)由与平行,可设的方程为.
将点代入上式得.
∴所求直线的方程为.
(2)由与垂直,可设的方程为.
将点代入上式得.
∴所求直线的方程为.
练习巩固
练习4:已知直线.
(1)求证:不论为何值,直线总经过第一象限;
解: (1)证明:将直线的方程整理为,
∴直线的斜率为,且过定点,
而点在第一象限内,故不论为何值,恒过第一象限.
练习巩固
练习4:已知直线.
(2)为使直线不经过第二象限,求的取值范围.
解: 直线的斜率为.
如图所示,要使不经过第二象限,需斜率,
∴,即的取值范围为.
练习巩固
变式4:已知直线.若直线不经过第二象限,求的取值范围.
解:①当,即时,直线方程为,该直线不经过第二象限,
满足要求.
②当,即时,直线化为截距式方程,
因为直线不过第二象限,故该直线的斜率大于等于零,且在轴的截距小于等于零,即解得所以.
由①②可得,的取值范围为.
小结
形式 方程 适用条件
点斜式 斜率存在的直线
斜截式 斜率存在的直线
两点式 斜率存在且不为
截距式 斜率存在且不为,不过原点
一般式 (,不同时为) 所有
