第二十二章 二次函数综合测评卷(二)(含答案)
文档属性
| 名称 | 第二十二章 二次函数综合测评卷(二)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 630.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 00:00:00 | ||
图片预览


文档简介
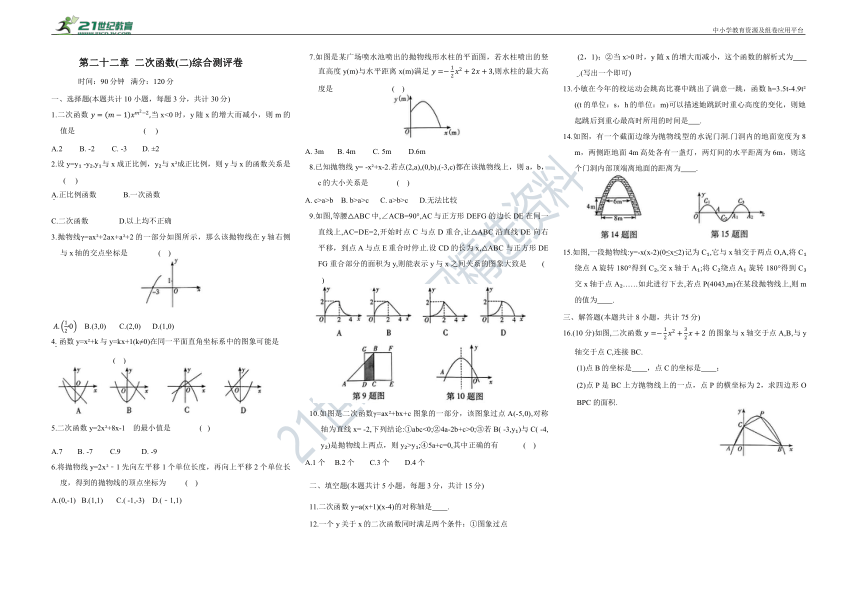
第二十二章 二次函数(二)综合测评卷
时间:90分钟 满分:120分
一、选择题(本题共计10 小题,每题3分,共计30分)
1.二次函数 当x<0时,y随x的增大而减小,则m的值是 ( )
A.2 B. -2 C. -3 D. ±2
2.设y=y -y ,y 与x成正比例,y 与x 成正比例,则y与x的函数关系是 ( )
A.正比例函数 B.一次函数
C.二次函数 D.以上均不正确
3.抛物线γ=ax +2ax+a +2的一部分如图所示,那么该抛物线在y轴右侧与x轴的交点坐标是 ( )
B.(3,0) C.(2,0) D.(1,0)
4. 函数y=x +k与y=kx+1(k≠0)在同一平面直角坐标系中的图象可能是 ( )
5.二次函数y=2x +8x-1 的最小值是 ( )
A.7 B. -7 C.9 D. -9
6.将抛物线y=2x ﹣1先向左平移1个单位长度,再向上平移2个单位长度,得到的抛物线的顶点坐标为 ( )
A.(0,-1) B.(1,1) C.( -1,-3) D.(﹣1,1)
7.如图是某广场喷水池喷出的抛物线形水柱的平面图,若水柱喷出的竖直高度y(m)与水平距离x(m)满足 则水柱的最大高度是 ( )
A. 3m B. 4m C. 5m D.6m
8.已知抛物线y= -x +x-2.若点(2,a),(0,b),(-3,c)都在该抛物线上,则a,b,c的大小关系是 ( )
A. c>a>b B. b>a>c C. a>b>c D.无法比较
9.如图,等腰△ABC中,∠ACB=90°,AC与正方形 DEFG 的边长DE 在同一直线上,AC=DE=2,开始时点C 与点 D 重合,让△ABC沿直线 DE 向右平移,到点 A 与点 E重合时停止.设CD的长为x,△ABC 与正方形 DEFG 重合部分的面积为 y,则能表示y与x之间关系的图象大致是 ( )
10.如图是二次函数γ=ax +bx+c图象的一部分,该图象过点A(-5,0),对称轴为直线x= -2,下列结论:①abc<0;②4a-2b+c>0;③若B( -3,y )与C( -4,y )是抛物线上两点,则y >y ;④5a+c=0,其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共计5小题,每题3分,共计15分)
11.二次函数y=a(x+1)(x-4)的对称轴是 .
12.一个y关于x的二次函数同时满足两个条件:①图象过点
(2,1);②当x>0时,y随x的增大而减小,这个函数的解析式为 .(写出一个即可)
13.小敏在今年的校运动会跳高比赛中跳出了满意一跳,函数h=3.5t-4.9t ((t的单位:s,h的单位:m)可以描述她跳跃时重心高度的变化,则她起跳后到重心最高时所用的时间是 .
14.如图,有一个截面边缘为抛物线型的水泥门洞.门洞内的地面宽度为8m,两侧距地面4m高处各有一盏灯,两灯间的水平距离为6m,则这个门洞内部顶端离地面的距离为 .
15.如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为 C ,它与x轴交于两点O,A,将 C 绕点A 旋转 180°得到 C ,交x轴于A ;将 C 绕点 A 旋转 180°得到 C 交x轴于点A ……如此进行下去,若点P(4043,m)在某段抛物线上,则m的值为 .
三、解答题(本题共计8 小题,共计75分)
16.(10分)如图,二次函数 的图象与x轴交于点A,B,与y轴交于点C,连接BC.
(1)点B的坐标是 ,点C的坐标是 ;
(2)点P是BC上方抛物线上的一点,点P 的横坐标为2,求四边形 OBPC 的面积.
中小学教育资源及组卷应用平台
17.(10分)工厂生产一种火爆的网红电子产品,每件产品成本16元,工厂将该产品进行网络批发,批发单价y(元)与一次性批发量x(件)(为正整数)之间满足如图所示的函数关系.
(1)直接写出y与x之间所满足的函数关系式,并写出自变量x的取值范围;
(2)若一次性批发量不超过60件,当批发量为多少件时,工厂获利最大?最大利润是多少?
18.(10分)设二次函数y=(m-1)x +(m-2)x-1,记其图象为C.
(1)若图象C与x轴只有一个交点,求实数 m 的取值范围;
(2)求证:图象C恒过x轴上的定点,并求该定点的坐标;,
(3)若图象C上所有点均在直线y=mx+1 的下方,求实数m的取值范围.
19.(11分)如图,已知抛物线y=ax +bx+c与x轴的一个交点为A(3,0),与y轴的交点为 B(0,3),其顶点为 C,对称轴为x=1.
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM 为等腰三角形时,直接写出点M的坐标.
20.(11 分)小明对函数 y=-|x -4|的图象和性质进行了探究,其探究过程中的列表如下:
x … -3 -2 -1 0 1 2 3 ··
y ... m 0. -3 n -3 0 -5 …
(1)求表中m,n的值;
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出该函数的图象;
(3)观察函数图象,写出一条函数的性质;
(4)结合你所画的函数图象,直接写出不等式-|x -4|>x-2的解集.
21. (11分)九年级数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如表:
时间x(天) 1≤x<50 50≤x≤90
售价(元/件) x+40 90
每天销量(件) 200-2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元 请直接写出结果.
22.(12分)如图,在平面直角坐标系中,抛物线y=ax +bx-2交x轴于A,B两点,交y轴于点C,且OA=2OC=8OB,点P是第三象限内抛物线上的一动点.
(1)求此抛物线的表达式;
(2)若PC∥AB,求点P的坐标;
(3)连接AC,求△PAC 面积的最大值及此时点P的坐标.
1-10ACDBDDCBAB
12. y= -x +5(答案不唯一)13. s 14. m 15.-1
16.解:(1)(4,0),(0,2);
(2)
17.解
(2)一次批发34件时所获利润最大,最大利润是 578 元.
18.(1)m=0时,图象C与x轴只有一个交点;
(2)证明:令y=0,得
(m-1)x +(m-2)x-1=0,
∴[(m-1)x-1](x+1)=0,
∴当x=-1时,y=0,
∴无论 m取何值,函数图象恒过点(-1,0);
(3)解:根据题意可知m-1<0,且y=mx+1与y=(m-1)x +(m-2)x-1无公共点,
由m-1<0得 m<1,
由方程y=mx+1与y=(m-1)x +(m-2)x-1无公共点可知
方程((m-1)x +(m-2)x-1-mx-1=0;无解,整理得(m-1)x -2x-2=0无解,
∴Δ=4+8(m-1) <0,解得
∴m的取值范围是
19.解:(1)由题意知,抛物线y=ax +bx+c与x轴的另一个交点为( -1,0),
解得
故抛物线的解析式为y= -x +2x+3;
(2)设 M点坐标为(0,t),
①当 MA=MB时,
解得 t=0,故M(0,0);
②当AB=AM时,
解得t=3(舍去)或t= -3,故M(0,-3);
③当AB=BM时,
解得 故 或M(0,3-3 ),所以点M 的坐标为(0,0)或(0,-3)
或 或
20.解:(1)把x=-3 和x=0分别代入y=-|x -4|中得y=-5,y= -4,
∴m= -5,n= -4;
(2)略
(3)当x取任意实数时,都有y≤0;(答案不唯一)
(4)如图,在同一平面直角坐标系中画出函数y=x-2 的图象,由图象知,-|x -4|>x-2的解集为-321.解:(1)当1≤x<50时,
y=(200-2x)(x+40-30)
= -2x +180x+2000;
当50≤x≤90时,
y=(200-2x)(90-30) = -120x+12000,
综上所述
(2)当1≤x<50时,二次函数开口向下,二次函数对称轴为x=45,
当x=45时,
当50≤x≤90时,y随x的增大而减小,
当x=50时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是 6050 元;
(3)当1≤x<50时,y= -2x +180x +2000≥4800,解得 20≤x≤70,
因此利润不低于 4800 元的天数是 20≤x<50,共30天;
当50≤x≤90时,y= -120x+12000≥4800,解得 x≤60,
因此利润不低于4800 元的天数是50≤x≤60,共11天,
因为30+11=41(天),
所以该商品在销售过程中,共41天每天销售
利润不低于4800元.
22.解:(1)在抛物线y=ax +bx-2中,
令x=0,则y=-2,
∴点C的坐标为(0,-2),∴OC=2.
∵OA=2OC=8OB,
∴点A的坐标为( -4,0),点B的坐标为(
把点A,B代入解析式,得
解得
(2)∵PC∥AB,点C 的坐标为(0,-2),
∴点P的纵坐标为 -2,
令y= -2,则
解得
∴点P的坐标为
(3)点P的坐标为( ﹣2,﹣5).
时间:90分钟 满分:120分
一、选择题(本题共计10 小题,每题3分,共计30分)
1.二次函数 当x<0时,y随x的增大而减小,则m的值是 ( )
A.2 B. -2 C. -3 D. ±2
2.设y=y -y ,y 与x成正比例,y 与x 成正比例,则y与x的函数关系是 ( )
A.正比例函数 B.一次函数
C.二次函数 D.以上均不正确
3.抛物线γ=ax +2ax+a +2的一部分如图所示,那么该抛物线在y轴右侧与x轴的交点坐标是 ( )
B.(3,0) C.(2,0) D.(1,0)
4. 函数y=x +k与y=kx+1(k≠0)在同一平面直角坐标系中的图象可能是 ( )
5.二次函数y=2x +8x-1 的最小值是 ( )
A.7 B. -7 C.9 D. -9
6.将抛物线y=2x ﹣1先向左平移1个单位长度,再向上平移2个单位长度,得到的抛物线的顶点坐标为 ( )
A.(0,-1) B.(1,1) C.( -1,-3) D.(﹣1,1)
7.如图是某广场喷水池喷出的抛物线形水柱的平面图,若水柱喷出的竖直高度y(m)与水平距离x(m)满足 则水柱的最大高度是 ( )
A. 3m B. 4m C. 5m D.6m
8.已知抛物线y= -x +x-2.若点(2,a),(0,b),(-3,c)都在该抛物线上,则a,b,c的大小关系是 ( )
A. c>a>b B. b>a>c C. a>b>c D.无法比较
9.如图,等腰△ABC中,∠ACB=90°,AC与正方形 DEFG 的边长DE 在同一直线上,AC=DE=2,开始时点C 与点 D 重合,让△ABC沿直线 DE 向右平移,到点 A 与点 E重合时停止.设CD的长为x,△ABC 与正方形 DEFG 重合部分的面积为 y,则能表示y与x之间关系的图象大致是 ( )
10.如图是二次函数γ=ax +bx+c图象的一部分,该图象过点A(-5,0),对称轴为直线x= -2,下列结论:①abc<0;②4a-2b+c>0;③若B( -3,y )与C( -4,y )是抛物线上两点,则y >y ;④5a+c=0,其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共计5小题,每题3分,共计15分)
11.二次函数y=a(x+1)(x-4)的对称轴是 .
12.一个y关于x的二次函数同时满足两个条件:①图象过点
(2,1);②当x>0时,y随x的增大而减小,这个函数的解析式为 .(写出一个即可)
13.小敏在今年的校运动会跳高比赛中跳出了满意一跳,函数h=3.5t-4.9t ((t的单位:s,h的单位:m)可以描述她跳跃时重心高度的变化,则她起跳后到重心最高时所用的时间是 .
14.如图,有一个截面边缘为抛物线型的水泥门洞.门洞内的地面宽度为8m,两侧距地面4m高处各有一盏灯,两灯间的水平距离为6m,则这个门洞内部顶端离地面的距离为 .
15.如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为 C ,它与x轴交于两点O,A,将 C 绕点A 旋转 180°得到 C ,交x轴于A ;将 C 绕点 A 旋转 180°得到 C 交x轴于点A ……如此进行下去,若点P(4043,m)在某段抛物线上,则m的值为 .
三、解答题(本题共计8 小题,共计75分)
16.(10分)如图,二次函数 的图象与x轴交于点A,B,与y轴交于点C,连接BC.
(1)点B的坐标是 ,点C的坐标是 ;
(2)点P是BC上方抛物线上的一点,点P 的横坐标为2,求四边形 OBPC 的面积.
中小学教育资源及组卷应用平台
17.(10分)工厂生产一种火爆的网红电子产品,每件产品成本16元,工厂将该产品进行网络批发,批发单价y(元)与一次性批发量x(件)(为正整数)之间满足如图所示的函数关系.
(1)直接写出y与x之间所满足的函数关系式,并写出自变量x的取值范围;
(2)若一次性批发量不超过60件,当批发量为多少件时,工厂获利最大?最大利润是多少?
18.(10分)设二次函数y=(m-1)x +(m-2)x-1,记其图象为C.
(1)若图象C与x轴只有一个交点,求实数 m 的取值范围;
(2)求证:图象C恒过x轴上的定点,并求该定点的坐标;,
(3)若图象C上所有点均在直线y=mx+1 的下方,求实数m的取值范围.
19.(11分)如图,已知抛物线y=ax +bx+c与x轴的一个交点为A(3,0),与y轴的交点为 B(0,3),其顶点为 C,对称轴为x=1.
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM 为等腰三角形时,直接写出点M的坐标.
20.(11 分)小明对函数 y=-|x -4|的图象和性质进行了探究,其探究过程中的列表如下:
x … -3 -2 -1 0 1 2 3 ··
y ... m 0. -3 n -3 0 -5 …
(1)求表中m,n的值;
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出该函数的图象;
(3)观察函数图象,写出一条函数的性质;
(4)结合你所画的函数图象,直接写出不等式-|x -4|>x-2的解集.
21. (11分)九年级数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如表:
时间x(天) 1≤x<50 50≤x≤90
售价(元/件) x+40 90
每天销量(件) 200-2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元 请直接写出结果.
22.(12分)如图,在平面直角坐标系中,抛物线y=ax +bx-2交x轴于A,B两点,交y轴于点C,且OA=2OC=8OB,点P是第三象限内抛物线上的一动点.
(1)求此抛物线的表达式;
(2)若PC∥AB,求点P的坐标;
(3)连接AC,求△PAC 面积的最大值及此时点P的坐标.
1-10ACDBDDCBAB
12. y= -x +5(答案不唯一)13. s 14. m 15.-1
16.解:(1)(4,0),(0,2);
(2)
17.解
(2)一次批发34件时所获利润最大,最大利润是 578 元.
18.(1)m=0时,图象C与x轴只有一个交点;
(2)证明:令y=0,得
(m-1)x +(m-2)x-1=0,
∴[(m-1)x-1](x+1)=0,
∴当x=-1时,y=0,
∴无论 m取何值,函数图象恒过点(-1,0);
(3)解:根据题意可知m-1<0,且y=mx+1与y=(m-1)x +(m-2)x-1无公共点,
由m-1<0得 m<1,
由方程y=mx+1与y=(m-1)x +(m-2)x-1无公共点可知
方程((m-1)x +(m-2)x-1-mx-1=0;无解,整理得(m-1)x -2x-2=0无解,
∴Δ=4+8(m-1) <0,解得
∴m的取值范围是
19.解:(1)由题意知,抛物线y=ax +bx+c与x轴的另一个交点为( -1,0),
解得
故抛物线的解析式为y= -x +2x+3;
(2)设 M点坐标为(0,t),
①当 MA=MB时,
解得 t=0,故M(0,0);
②当AB=AM时,
解得t=3(舍去)或t= -3,故M(0,-3);
③当AB=BM时,
解得 故 或M(0,3-3 ),所以点M 的坐标为(0,0)或(0,-3)
或 或
20.解:(1)把x=-3 和x=0分别代入y=-|x -4|中得y=-5,y= -4,
∴m= -5,n= -4;
(2)略
(3)当x取任意实数时,都有y≤0;(答案不唯一)
(4)如图,在同一平面直角坐标系中画出函数y=x-2 的图象,由图象知,-|x -4|>x-2的解集为-3
y=(200-2x)(x+40-30)
= -2x +180x+2000;
当50≤x≤90时,
y=(200-2x)(90-30) = -120x+12000,
综上所述
(2)当1≤x<50时,二次函数开口向下,二次函数对称轴为x=45,
当x=45时,
当50≤x≤90时,y随x的增大而减小,
当x=50时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是 6050 元;
(3)当1≤x<50时,y= -2x +180x +2000≥4800,解得 20≤x≤70,
因此利润不低于 4800 元的天数是 20≤x<50,共30天;
当50≤x≤90时,y= -120x+12000≥4800,解得 x≤60,
因此利润不低于4800 元的天数是50≤x≤60,共11天,
因为30+11=41(天),
所以该商品在销售过程中,共41天每天销售
利润不低于4800元.
22.解:(1)在抛物线y=ax +bx-2中,
令x=0,则y=-2,
∴点C的坐标为(0,-2),∴OC=2.
∵OA=2OC=8OB,
∴点A的坐标为( -4,0),点B的坐标为(
把点A,B代入解析式,得
解得
(2)∵PC∥AB,点C 的坐标为(0,-2),
∴点P的纵坐标为 -2,
令y= -2,则
解得
∴点P的坐标为
(3)点P的坐标为( ﹣2,﹣5).
同课章节目录
