第11章 反比例函数 单元训练 苏科版数学八年级下册(含解析)
文档属性
| 名称 | 第11章 反比例函数 单元训练 苏科版数学八年级下册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 875.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览




文档简介
第11章 反比例函数 单元训练——苏科版数学八年级下
一、选择题
1.下列关于反比例函数的描述中,不正确的是( )
A.图象在第二、四象限
B.点在反比例函数的图象上
C.随的增大而增大
D.当时,
2.在平面直角坐标系中,反比例函数的图象经过点,则它的图象也一定经过的点是( )
A. B. C. D.
3.在同一坐标系中,函数y=和y=kx 2的图象大致是( )
A. B.
C. D.
4.已知A(1,y1),B(2,y2)两点在双曲线y上,且y1>y2,则m的取值范围是( )
A.m<0 B.m>0 C.m D.m
5.已知反比例函数的图象经过点,则这个函数的图象位于( )
A.第二、三象限 B.第一、三象限
C.第三、四象限 D.第二、四象限
6.已知矩形的长为,宽为,面积为,则与之间的函数关系用图象表示大致是( )
A. B. C. D.
7.探究函数的图像发现,可以由的图像先向右平移2个单位,再向上平移3个单位得到.根据以上信息判断,下列直线中与函数的图像没有公共点的是( )
A.经过点且平行于x轴的直线
B.经过点且平行于x轴的直线
C.经过点且平行于y轴的直线
D.经过点且平行于y轴的直线
8.如图,点在反比例函数,的图象上,点在反比例函数的图象上,轴于点且,则的值为( )
A. B. C. D.
9.近视眼镜是一种为了矫正视力,让人们可以清晰看到远距离物体的凹透镜片.研究发现,近视眼镜的度数y(度)与镜片焦距x(m)的函数关系如图所示,则下列说法中错误的是( )
A.镜片焦距x的值越大,近视眼镜的度数y的值越小
B.图中曲线是反比例函数的图象(其中一支)
C.当焦距x为时,近视眼镜的度数y约为300度
D.对于每一个镜片焦距x,都有唯一的近视度数y与它对应
10.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,其图像如图所示.当气球内的气压大于时,气球将爆炸,为确保气球不爆炸,气球的体积应( )
A.不小于 B.不大于
C.不小于 D.不大于
11.在平面直角坐标系中,反比例函数 的图象上有三点 ,若 且 ,则B的取值范围为( )
A. B.
C. D.
二、填空题
12.若函数是反比例函数,则m的值是 .
13.已知函数满足下列两个条件:①当x>0时,y随x的增大而增大;②它的图象经过点(1,﹣2),请写出一个符合上述条件的函数的表达式 .
14.如图,已知一次函数与反比例函数相交于点,,则不等式的解集是 .
15.如图,在矩形中,,F是上的一个动点(F不与A,B重合),过点F的反比例函数的图像与边交于点E,若时,则k= .
三、解答题
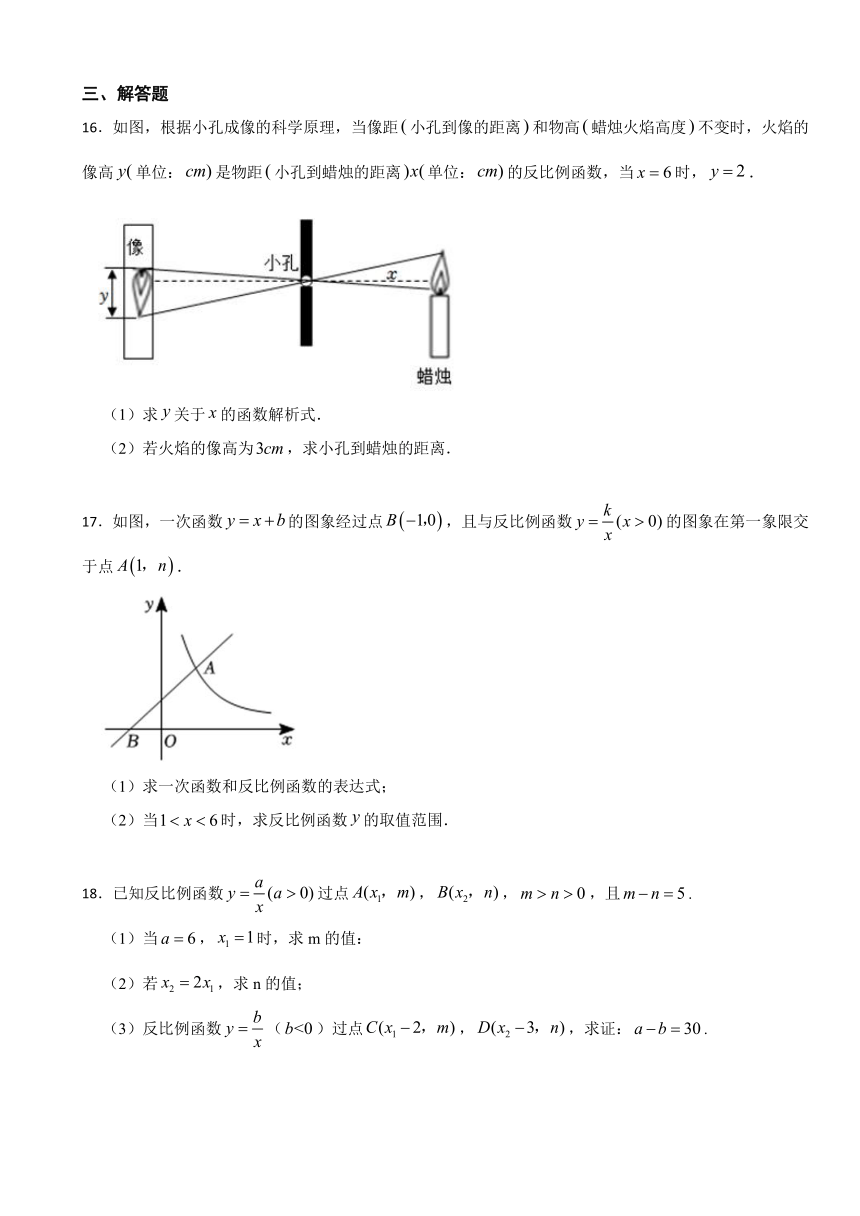
16.如图,根据小孔成像的科学原理,当像距小孔到像的距离和物高蜡烛火焰高度不变时,火焰的像高单位:是物距小孔到蜡烛的距离单位:的反比例函数,当时,.
(1)求关于的函数解析式.
(2)若火焰的像高为,求小孔到蜡烛的距离.
17.如图,一次函数的图象经过点,且与反比例函数的图象在第一象限交于点.
(1)求一次函数和反比例函数的表达式;
(2)当时,求反比例函数的取值范围.
18.已知反比例函数过点,,,且.
(1)当,时,求m的值:
(2)若,求n的值;
(3)反比例函数()过点,,求证:.
19.已知,视力表上视力值和字母的宽度(mm)之间的关系是我们已经学过的一类函数模型,字母的宽度如图1所示,经整理,视力表上部分视力值和字母的宽度(mm)的对应数据如表所示:
位置 视力值 的值(mm)
第1行 0.1 70
第5行 0.25 28
第8行 0.5 14
第14行 2.0 3.5
(1)请你根据表格数据判断并求出视力值和字母的宽度(mm)之间的函数表达式,并说明理由;
(2)经过测量,第4行和第7行两行首个字母E的宽度a(mm)的值分别是35mm和17.5mm,求第4行、第7行的视力值.
答案解析部分
1.【答案】C
【解析】解:A:因为k=-3<0,所以函数图象在二、四象限,A正确
B:当x=-1时,带入函数解析式得y=3,B正确
C:在每一象限内,y随x的增大而增大,C错误
D:当时,,D正确
故答案为C
2.【答案】B
【解析】解:由题意可得:
,解得:k=-6
A:当x=6时,y=-1,A错误,不符合题意;
B:当x=1时,y=-6,B正确,符合题意;
C:当x=-3时,y=2,C错误,不符合题意;
D:当x=-2时,y=3,D错误,不符合题意;
故答案为:B
3.【答案】B
【解析】解:∵y=kx-2与y轴交于负半轴,排除A,D选项,
当k>0时,反比例函数在第一、三象限,一次函数经过一、三象限,
当k<0时,反比例函数在第二、四象限,一次函数经过二、四象限,
故答案为:B.
4.【答案】C
【解析】解:∵A(1,y1),B(2,y2)两点在双曲线y上,且y1>y2,
∴3+2m>0,
解得:m,
故答案为:C.
5.【答案】B
【解析】解:∵反比例函数的图象经过点 ,
∴k=-2×(-1)=2>0,
∴此函数的图象位于一、三象限.
故答案为:B.
6.【答案】A
【解析】解:由题意知:(x>0,y>0),因为k=9>0,反比例函数图象在第一、三象限,根据实际情况可知,该函数图象只能在第一象限,故A选项正确.
故答案为:A.
7.【答案】B
【解析】解:根据题意可知,如下图所示,图1根据题意平移后得到图2,
函数的图象是函数的图象向右平移1个单位,在向下平移3个单位得到的,
∴由反比例函数的图象的性质和平移的定义可知,函数的图象与直线 x= 1、直线y =-3不会相交.
故答案为:B.
8.【答案】B
【解析】解:由题意可得:
∵反比例函数的图象在第四象限
故答案为:B
9.【答案】C
【解析】解:C:由图像可知,当x=0.3时,y值比300大,故C错误
故答案为:C
10.【答案】C
【解析】解:设P=,将(1.5,16000)代入可得k=24000,
∴p=.
令p=40000,可得V=0.6,
∴气球的体积应不小于0.6m3.
故答案为:C.
11.【答案】D
【解析】解:如图,
点P(2,2)在反比例函数 的图象上,
∴ ,
∵点Q( , )在反比例函数 图象上,
∴ ,
∴Q( , ),
∵双曲线关于 轴对称,
∴与 ( , )对称的 的坐标为( , ),
∵点M( , )在反比例函数 图象上,且 ,PM>PQ,
∴点M在第三象限 左边的曲线上,或在 右侧的曲线上,
∴点M的纵坐标 的取值范围为: 或 .
故答案为:D.
12.【答案】0
【解析】解:∵函数是反比例函数,
∴且,
解得:m=0.
故答案为:0
13.【答案】
【解析】解:∵当x>0时,y随x的增大而增大,
∴反比例函数的比例系数k<0,
∵反比例函数的图象经过点(1,﹣2),
∴,
∴反比例函数的解析式为,
故答案为:.
14.【答案】x>0或-4<x<-1
【解析】解: ∵不等式,
∴,
由图象知:当x>0或-4<x<-1时,直线 的图象在反比例函数图象的上方,
∴不等式的解集为:x>0或-4<x<-1;
故答案为:x>0或-4<x<-1.
15.【答案】4
【解析】解:在矩形OABC中,OA=3,OC=2,
则设E(a,2),F(3,b)
∵点 E、F在反比例函数图象上,
∴
∴
∵
即
∴ k= 4或k=0,
k=0不符合题意,舍去,
∴ k= 4
故答案为:4.
16.【答案】(1)解:由题意设:,
把,代入,得,
关于的函数解析式为:;
(2)解:把代入,得,,
小孔到蜡烛的距离为.
17.【答案】(1)解:把点代入一次函数,
得,
∴,
∴一次函数解析式为:,
∵点在一次函数的图象上,
∴,
∴点的坐标是.
∵反比例函数的图象过点.
∴,
∴反比例函数关系式是:;
(2)解:由(1)知反比例函数,
当时,随的增大而减小,
而当时,,当时,,
∴当时,反比例函数的值:.
18.【答案】(1)解:反比例函数过点,,,
∴,
(2)解:反比例函数过点,,
,,
,
,
化简,得,
,
;
(3)解:反比例函数过点,,
,,
反比例函数过点,,
,,
,,
,,
,
又,
,,
19.【答案】(1)解:根据表格数据可知,视力值和随着宽度减小而增大,且视力值和宽度的积为定值,故视力值和宽度成反比例函数关系,
设视力值和宽度的函数解析式为:,
将点,代入求得,
故视力值和宽度的函数解析式为:
(2)解:∵第4行首个字母E的宽度a(mm)的值是35mm,
即,将代入,求得;
∵第7行首个字母E的宽度a(mm)的值是17.5mm,
即,将代入,求得;
故求第4行、第7行的视力值分别是,
一、选择题
1.下列关于反比例函数的描述中,不正确的是( )
A.图象在第二、四象限
B.点在反比例函数的图象上
C.随的增大而增大
D.当时,
2.在平面直角坐标系中,反比例函数的图象经过点,则它的图象也一定经过的点是( )
A. B. C. D.
3.在同一坐标系中,函数y=和y=kx 2的图象大致是( )
A. B.
C. D.
4.已知A(1,y1),B(2,y2)两点在双曲线y上,且y1>y2,则m的取值范围是( )
A.m<0 B.m>0 C.m D.m
5.已知反比例函数的图象经过点,则这个函数的图象位于( )
A.第二、三象限 B.第一、三象限
C.第三、四象限 D.第二、四象限
6.已知矩形的长为,宽为,面积为,则与之间的函数关系用图象表示大致是( )
A. B. C. D.
7.探究函数的图像发现,可以由的图像先向右平移2个单位,再向上平移3个单位得到.根据以上信息判断,下列直线中与函数的图像没有公共点的是( )
A.经过点且平行于x轴的直线
B.经过点且平行于x轴的直线
C.经过点且平行于y轴的直线
D.经过点且平行于y轴的直线
8.如图,点在反比例函数,的图象上,点在反比例函数的图象上,轴于点且,则的值为( )
A. B. C. D.
9.近视眼镜是一种为了矫正视力,让人们可以清晰看到远距离物体的凹透镜片.研究发现,近视眼镜的度数y(度)与镜片焦距x(m)的函数关系如图所示,则下列说法中错误的是( )
A.镜片焦距x的值越大,近视眼镜的度数y的值越小
B.图中曲线是反比例函数的图象(其中一支)
C.当焦距x为时,近视眼镜的度数y约为300度
D.对于每一个镜片焦距x,都有唯一的近视度数y与它对应
10.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强是气球体积的反比例函数,其图像如图所示.当气球内的气压大于时,气球将爆炸,为确保气球不爆炸,气球的体积应( )
A.不小于 B.不大于
C.不小于 D.不大于
11.在平面直角坐标系中,反比例函数 的图象上有三点 ,若 且 ,则B的取值范围为( )
A. B.
C. D.
二、填空题
12.若函数是反比例函数,则m的值是 .
13.已知函数满足下列两个条件:①当x>0时,y随x的增大而增大;②它的图象经过点(1,﹣2),请写出一个符合上述条件的函数的表达式 .
14.如图,已知一次函数与反比例函数相交于点,,则不等式的解集是 .
15.如图,在矩形中,,F是上的一个动点(F不与A,B重合),过点F的反比例函数的图像与边交于点E,若时,则k= .
三、解答题
16.如图,根据小孔成像的科学原理,当像距小孔到像的距离和物高蜡烛火焰高度不变时,火焰的像高单位:是物距小孔到蜡烛的距离单位:的反比例函数,当时,.
(1)求关于的函数解析式.
(2)若火焰的像高为,求小孔到蜡烛的距离.
17.如图,一次函数的图象经过点,且与反比例函数的图象在第一象限交于点.
(1)求一次函数和反比例函数的表达式;
(2)当时,求反比例函数的取值范围.
18.已知反比例函数过点,,,且.
(1)当,时,求m的值:
(2)若,求n的值;
(3)反比例函数()过点,,求证:.
19.已知,视力表上视力值和字母的宽度(mm)之间的关系是我们已经学过的一类函数模型,字母的宽度如图1所示,经整理,视力表上部分视力值和字母的宽度(mm)的对应数据如表所示:
位置 视力值 的值(mm)
第1行 0.1 70
第5行 0.25 28
第8行 0.5 14
第14行 2.0 3.5
(1)请你根据表格数据判断并求出视力值和字母的宽度(mm)之间的函数表达式,并说明理由;
(2)经过测量,第4行和第7行两行首个字母E的宽度a(mm)的值分别是35mm和17.5mm,求第4行、第7行的视力值.
答案解析部分
1.【答案】C
【解析】解:A:因为k=-3<0,所以函数图象在二、四象限,A正确
B:当x=-1时,带入函数解析式得y=3,B正确
C:在每一象限内,y随x的增大而增大,C错误
D:当时,,D正确
故答案为C
2.【答案】B
【解析】解:由题意可得:
,解得:k=-6
A:当x=6时,y=-1,A错误,不符合题意;
B:当x=1时,y=-6,B正确,符合题意;
C:当x=-3时,y=2,C错误,不符合题意;
D:当x=-2时,y=3,D错误,不符合题意;
故答案为:B
3.【答案】B
【解析】解:∵y=kx-2与y轴交于负半轴,排除A,D选项,
当k>0时,反比例函数在第一、三象限,一次函数经过一、三象限,
当k<0时,反比例函数在第二、四象限,一次函数经过二、四象限,
故答案为:B.
4.【答案】C
【解析】解:∵A(1,y1),B(2,y2)两点在双曲线y上,且y1>y2,
∴3+2m>0,
解得:m,
故答案为:C.
5.【答案】B
【解析】解:∵反比例函数的图象经过点 ,
∴k=-2×(-1)=2>0,
∴此函数的图象位于一、三象限.
故答案为:B.
6.【答案】A
【解析】解:由题意知:(x>0,y>0),因为k=9>0,反比例函数图象在第一、三象限,根据实际情况可知,该函数图象只能在第一象限,故A选项正确.
故答案为:A.
7.【答案】B
【解析】解:根据题意可知,如下图所示,图1根据题意平移后得到图2,
函数的图象是函数的图象向右平移1个单位,在向下平移3个单位得到的,
∴由反比例函数的图象的性质和平移的定义可知,函数的图象与直线 x= 1、直线y =-3不会相交.
故答案为:B.
8.【答案】B
【解析】解:由题意可得:
∵反比例函数的图象在第四象限
故答案为:B
9.【答案】C
【解析】解:C:由图像可知,当x=0.3时,y值比300大,故C错误
故答案为:C
10.【答案】C
【解析】解:设P=,将(1.5,16000)代入可得k=24000,
∴p=.
令p=40000,可得V=0.6,
∴气球的体积应不小于0.6m3.
故答案为:C.
11.【答案】D
【解析】解:如图,
点P(2,2)在反比例函数 的图象上,
∴ ,
∵点Q( , )在反比例函数 图象上,
∴ ,
∴Q( , ),
∵双曲线关于 轴对称,
∴与 ( , )对称的 的坐标为( , ),
∵点M( , )在反比例函数 图象上,且 ,PM>PQ,
∴点M在第三象限 左边的曲线上,或在 右侧的曲线上,
∴点M的纵坐标 的取值范围为: 或 .
故答案为:D.
12.【答案】0
【解析】解:∵函数是反比例函数,
∴且,
解得:m=0.
故答案为:0
13.【答案】
【解析】解:∵当x>0时,y随x的增大而增大,
∴反比例函数的比例系数k<0,
∵反比例函数的图象经过点(1,﹣2),
∴,
∴反比例函数的解析式为,
故答案为:.
14.【答案】x>0或-4<x<-1
【解析】解: ∵不等式,
∴,
由图象知:当x>0或-4<x<-1时,直线 的图象在反比例函数图象的上方,
∴不等式的解集为:x>0或-4<x<-1;
故答案为:x>0或-4<x<-1.
15.【答案】4
【解析】解:在矩形OABC中,OA=3,OC=2,
则设E(a,2),F(3,b)
∵点 E、F在反比例函数图象上,
∴
∴
∵
即
∴ k= 4或k=0,
k=0不符合题意,舍去,
∴ k= 4
故答案为:4.
16.【答案】(1)解:由题意设:,
把,代入,得,
关于的函数解析式为:;
(2)解:把代入,得,,
小孔到蜡烛的距离为.
17.【答案】(1)解:把点代入一次函数,
得,
∴,
∴一次函数解析式为:,
∵点在一次函数的图象上,
∴,
∴点的坐标是.
∵反比例函数的图象过点.
∴,
∴反比例函数关系式是:;
(2)解:由(1)知反比例函数,
当时,随的增大而减小,
而当时,,当时,,
∴当时,反比例函数的值:.
18.【答案】(1)解:反比例函数过点,,,
∴,
(2)解:反比例函数过点,,
,,
,
,
化简,得,
,
;
(3)解:反比例函数过点,,
,,
反比例函数过点,,
,,
,,
,,
,
又,
,,
19.【答案】(1)解:根据表格数据可知,视力值和随着宽度减小而增大,且视力值和宽度的积为定值,故视力值和宽度成反比例函数关系,
设视力值和宽度的函数解析式为:,
将点,代入求得,
故视力值和宽度的函数解析式为:
(2)解:∵第4行首个字母E的宽度a(mm)的值是35mm,
即,将代入,求得;
∵第7行首个字母E的宽度a(mm)的值是17.5mm,
即,将代入,求得;
故求第4行、第7行的视力值分别是,
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
