北师大版(2019)必修第二册《第六章 立体几何初步》单元测试卷(含解析)
文档属性
| 名称 | 北师大版(2019)必修第二册《第六章 立体几何初步》单元测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 333.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 18:02:06 | ||
图片预览



文档简介
北师大版(2019)必修第二册《第六章 立体几何初步》单元测试卷
一、单选题
1.已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,侧视图为直角三角形,则该三棱锥的表面积为( )
A.4+ B.4 C.8+ D.6
2.设α,β为两个不重合的平面,能使α∥β成立的是( )
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α内有无数个点到β的距离相等
D.α,β垂直于同一平面
3.已知m,n是两条不重合的直线,α,β是两个不重合的平面,则下列命题中正确为( )
A.若m∥β,n⊥α,α⊥β,则m⊥n
B.若m⊥α,n⊥β,则α∥β
C.若m∥α,n∥β,α∥β,则m∥n
D.若α⊥β,α∩β=m,n β,m⊥n,则n⊥α
4.圆柱底面周长为4π,高为4,则它的体积为( )
A.4π B.8π C.12π D.16π
5.若一个圆锥的轴截面是边长为的等边三角形,则这个圆锥的表面积为( )
A.6π B.5π C.4π D.
6.如图,AB是圆的直径,PA⊥AC,PA⊥BC,C是圆上一点(不同于A,B),且PA=AC,则二面角P﹣BC﹣A的平面角为( )
A.∠PAC B.∠CPA C.∠PCA D.∠CAB
7.在下列条件中,可判断平面α与β平行的是( )
A.α⊥γ,且β⊥γ
B.m,n是两条异面直线,且m∥β,n∥β,m∥α,n∥α
C.m,n是α内的两条直线,且m∥β,n∥β
D.α内存在不共线的三点到β的距离相等
8.如图,在三棱柱ABC﹣A1B1C1中,A1A⊥底面ABC,AB⊥AC,A1A=AB=AC=2,那么三棱锥A1﹣ABC的体积是( )
A. B. C.4 D.8
9.如图,ABCD﹣A1B1C1D1为正方体,则以下结论:①BD∥平面CB1D1;②AC1⊥BD;③AC1⊥平面CB1D1.其中正确结论的个数是( )
A.0 B.1 C.2 D.3
10.如图所示的正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF,EF把这个正方形折成一个四面体,使G1,G2,G3重合为点G,则有( )
A.SG⊥平面EFG B.EG⊥平面SEF C.GF⊥平面SEF D.SG⊥平面SEF
(多选)11.已知m,n是两条不重合的直线,α,β,γ是三个两两不重合的平面,则下列命题正确的是( )
A.若m⊥α,n⊥β,α∥β,则m∥n
B.若α⊥γ,β⊥γ,则α∥β
C.若m∥β,n∥β,m,n α,则α∥β
D.若n α,n⊥β,则α⊥β
(多选)12.已知m,n,l是三条直线,α是一个平面,下列命题不正确的是( )
A.若m∥l,n∥l,则m∥n B.若m⊥l,n⊥l,则m∥n
C.若m∥α,n∥α,则m∥n D.若m⊥α,n⊥α,则m∥n
二、填空题
13.三个平面两两垂直,它们的交线交于一点O,空间有一点P到三个面的距离分别为3、4、5,则OP的长为 .
14.设长方体的长、宽、高分别为3、2、1,其顶点都在同一个球面上,则该球的半径为 .
15.在底面为正方形的四棱锥P﹣ABCD中,PA⊥平面ABCD,PA=4,AB=3,则该四棱锥的外接球的表面积为 .
16.已知圆柱的两个底面的圆周在同一个球的球面上,圆柱的高和球半径均为2,则该圆柱的体积为 .
三、解答题
17.如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为BC,AC的中点,AB=BC.求证:
(1)A1B1∥平面DEC1;
(2)BE⊥C1E.
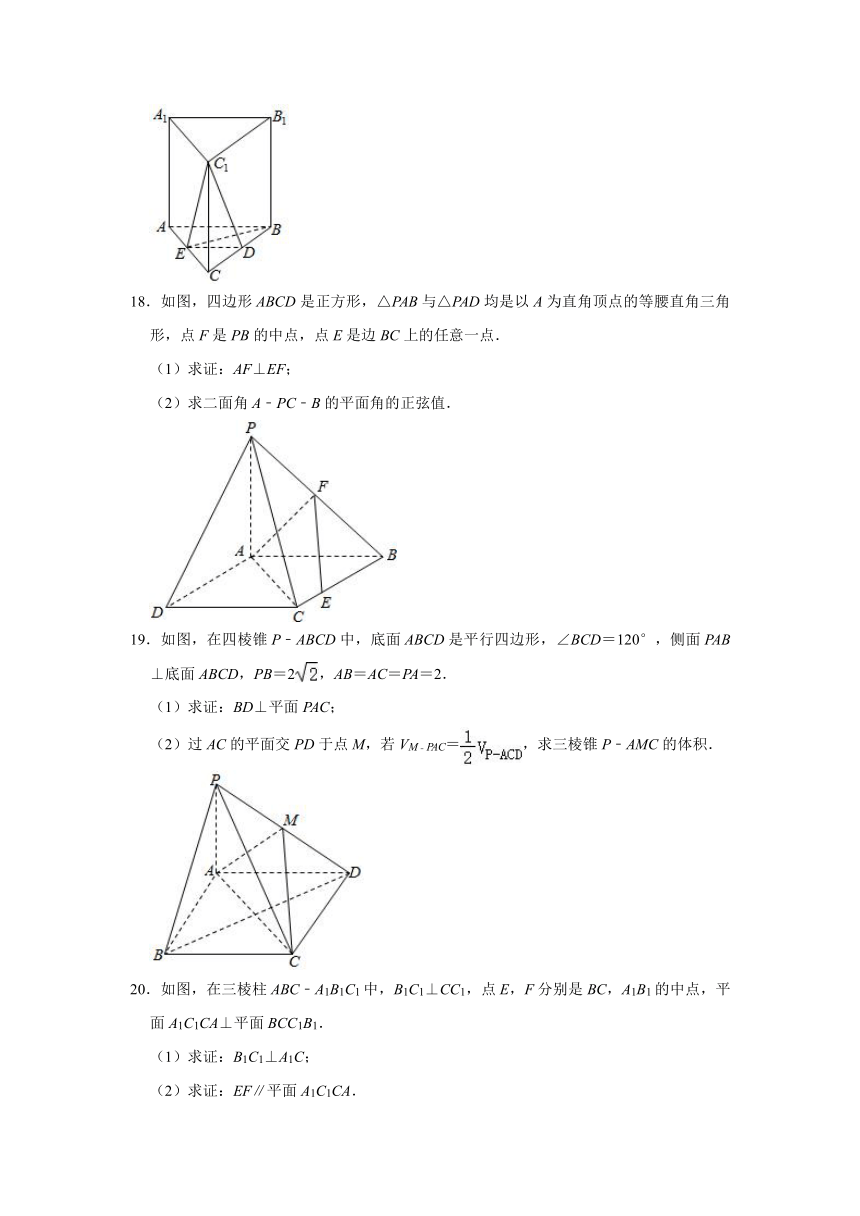
18.如图,四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点.
(1)求证:AF⊥EF;
(2)求二面角A﹣PC﹣B的平面角的正弦值.
19.如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=120°,侧面PAB⊥底面ABCD,PB=2,AB=AC=PA=2.
(1)求证:BD⊥平面PAC;
(2)过AC的平面交PD于点M,若VM﹣PAC=,求三棱锥P﹣AMC的体积.
20.如图,在三棱柱ABC﹣A1B1C1中,B1C1⊥CC1,点E,F分别是BC,A1B1的中点,平面A1C1CA⊥平面BCC1B1.
(1)求证:B1C1⊥A1C;
(2)求证:EF∥平面A1C1CA.
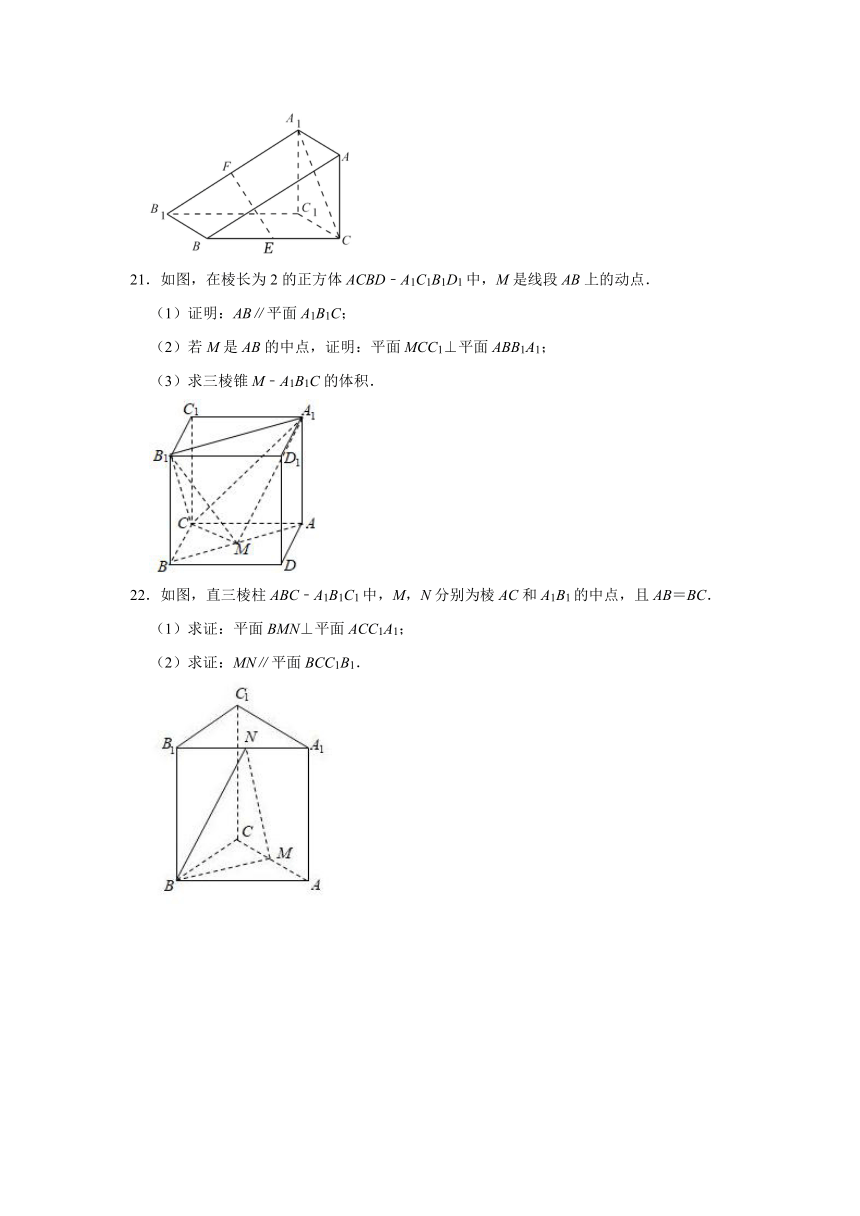
21.如图,在棱长为2的正方体ACBD﹣A1C1B1D1中,M是线段AB上的动点.
(1)证明:AB∥平面A1B1C;
(2)若M是AB的中点,证明:平面MCC1⊥平面ABB1A1;
(3)求三棱锥M﹣A1B1C的体积.
22.如图,直三棱柱ABC﹣A1B1C1中,M,N分别为棱AC和A1B1的中点,且AB=BC.
(1)求证:平面BMN⊥平面ACC1A1;
(2)求证:MN∥平面BCC1B1.
参考答案与试题解析
一、单选题
1. 解:根据三视图转换为几何体的直观图:
该三棱锥是底面为腰长为2、底为的等腰三角形,
侧面分别是两个腰为2的等腰直角三角形和一个底为、高为的三角形,
如图所示:
所以该三棱锥的表面积为,
故选:A.
2. 解:对于A,α内有无数条直线与β平行,如两个相交平面,可以找出无数条平行于交线的直线,所以A错误;
对于B,α内有两条相交直线与β平行,根据两平面平行的判定定理知,α∥β,所以B正确;
对于C,α内有无数个点到β的距离相等,如两个相交平面,可以找出无数条直线平行于平面β,所以也能得出无数个点到平面β的距离相等,C错误;
对于D,当α、β垂直于同一个平面时,α与β也可以相交,所以D错误.
故选:B.
3. 解:由m,n是两条不重合的直线,α,β是两个不重合的平面,得:
在A中,若m∥β,n⊥α,α⊥β,则m与n相交、平行或异面,故A错误;
在B中,若m⊥α,n⊥β,则α与β相交或平行,故B错误;
在C中,若m∥α,n∥β,α∥β,则m与n相交、平行或异面,故C错误;
在D中,若α⊥β,α∩β=m,n β,m⊥n,
则由面面垂直的性质定理得n⊥α,故D正确.
故选:D.
4. 解:设圆柱底面半径为r,所以底面圆周长为2πr=4π,解得r=2;
又圆柱的高为4,所以它的体积为V=πr2h=π×22×4=16π.
故选:D.
5. 解:∵一个圆锥的轴截面是边长为的等边三角形,
设等边三角形的边长为2r,则2r=2,
则它的高为r,底面半径r=,
所以这个圆锥的表面积为π r2+πr 2r=6π,
故选:A.
6. 解:∵点C在以AB为直径的圆上,∴AC⊥BC,
又PA⊥BC,AC∩PA=A,AC、PA 平面PAC,
∴BC⊥平面PAC,
∴BC⊥PC,
∵AC⊥BC,∴∠PCA为二面角P﹣BC﹣A的平面角.
故选:C.
7. 解:A中:教室的墙角的两个平面都垂直底面,但是不平行,错误.
B中,利用平面与平面平行的判定,可得正确;
C中:如果这两条直线平行,那么平面α与β可能相交,所以C错误.
D中:如果这三个点在平面的两侧,满足不共线的三点到β的距离相等,这两个平面相交,B错误.
故选:B.
8. 解:∵AB⊥AC,AB=AC=2,
∴,且A1A⊥底面ABC,A1A=2,
∴.
故选:A.
9. 解:由正方体的性质得,BD∥B1D1,所以结合线面平行的判定定理可得:BD∥平面CB1D1;所以①正确.
由正方体的性质得 AC⊥BD,因为AC是AC1在底面ABCD内的射影,所以由三垂线定理可得:AC1⊥BD,所以②正确.
由正方体的性质得 BD∥B1D1,由②可得AC1⊥BD,所以AC1⊥B1D1,同理可得AC1⊥CB1,进而结合线面垂直的判定定理得到:AC1⊥平面CB1D1,所以③正确.
故选:D.
10. 解:如图所示
∵始终有 SG1⊥G1E,SG3⊥G3F,
∴SG⊥GE,SG⊥GF
又 GE∩GF=G
∴SG⊥平面 EFG.
故选:A.
11. 解:对于A,m⊥α,α∥β,则m⊥β,又n⊥β,则m∥n,故A正确;
对于B,由α⊥γ,β⊥γ,得α∥β或α与β相交,故B错误;
对于C,由m∥β,n∥β,m,n α,若m与n相交,则α∥β,若m∥n,则α可能平行β,也可能与β相交,故C错误;
对于D,由平面与平面垂直的判定,可得若n α,n⊥β,则α⊥β,故D正确.
故选:AD.
12. 解:对于A,若m∥l,n∥l,由平行公理可得m∥n,故A正确;
对于B,若m⊥l,n⊥l,则m∥n或m与n相交或m与n异面,故B错误;
对于C,若m∥α,n∥α,则m∥n或m与n相交或m与n异面,故C错误;
对于D,若m⊥α,n⊥α,由直线与平面垂直的性质可得m∥n,故D正确.
故选:BC.
二、填空题
13. 解:根据题意,过点P分别作三个平面的垂线,垂足分别为B、D、F,
∵三个平面两两垂直,
∴分别以PB、PD、PF为长、宽、高,作长方体OABC﹣EDPF,如图所示.
∵点P到三个面的距离分别为3、4、5,
∴长方体的对角线长为=,
即OP的长为.
故答案为:5
14. 解:由长方体的对角线等于其外接球的直径2R可得:(2R)2=32+22+12,解得:R=,
故答案为:.
15. 解:底面为正方形的四棱锥P﹣ABCD中,PA⊥平面ABCD,PA=4,AB=3,
如图所示:
设外接球的半径为R,
所以(2R)2=42+32+32=34,
解得,
所以.
故答案为:34π.
16. 解:设圆柱上底面圆的半径为r,
则根据题意得r2+1=4,∴r2=3,
∴该圆柱的体积为V=3π 2=6π.
故答案为:6π.
三、解答题
17. 证明:(1)∵在直三棱柱ABC﹣A1B1C1中,D,E分别为BC,AC的中点,
∴DE∥AB,AB∥A1B1,∴DE∥A1B1,
∵DE 平面DEC1,A1B1 平面DEC1,
∴A1B1∥平面DEC1.
解:(2)∵在直三棱柱ABC﹣A1B1C1中,E是AC的中点,AB=BC.
∴BE⊥AC,
∵直三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,BE 平面ABC,
∴BE⊥AA1,
又AA1∩AC=A,∴BE⊥平面ACC1A1,
∵C1E 平面ACC1A1,∴BE⊥C1E.
18. (1)证明:∵四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,
∴PA⊥AD,PA⊥AB,又AD∩AB=A,AB⊥BC,
∴PA⊥平面ABCD,又BC 面ABCD,∴PA⊥BC,
∵AB∩PA=A,∴BC⊥面PAB,
∴BC⊥AF,
∵△PAB是以A为直角顶点的等腰直角三角形,F是PB中点,
∴AF⊥PB,
又PB∩BC=B,∴AF⊥平面PBC,
∵EF 平面PBC,∴AF⊥EF.
(2)解:以A为原点,AD为x轴,AB为y轴,P为z轴,
建立空间直角坐标系,
设AB=1,则A(0,0,0),B(0,1,0),C(1,1,0),P(0,0,1),
=(0,0,1),=(1,1,0),
设平面APC的法向量=(x,y,z),
则,取x=1,得=(1,﹣1,0),
=(0,1,﹣1),=(1,1,﹣1),
设平面PBC的法向量=(a,b,c),
则,取b=1,得=(0,1,1),
|cos<>|=||=,
∴<>=60°,又sin60°=,
∴二面角A﹣PC﹣B的平面角的正弦值为.
19. 证明:(1)由题意,底面ABCD是菱形,且AB=AC=2,∴BD⊥AC,
在△PAB中,∵AB=PA=2,,∴PA2+AB2=PB2,
即∠PAB=90°,∴PA⊥AB,
又平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,PA 平面PAB,
∴PA⊥平面ABCD,而BD 平面ABCD,则PA⊥BD,
又PA∩AC=A,∴BD⊥平面PAC;
解:(2)由(1)知:PA⊥平面ABCD,
∴==,
而VM﹣PAC=VP﹣AMC,且,
∴.
20. 证明:(1)因为BC1⊥C1C,又平面A1C1CA⊥平面BCC1B1,
且平面A1C1CA∩平面BCC1B1=C1C,
所以BC1⊥平面ACC1A1.
又因为A1C 平面A1C1CA,
所以BC1⊥A1C.
(2)取A1C1中点G,连FG,连GC,如图所示:
在△A1B1C1中,因为F,G分别是A1B1,A1C1中点,
所以FG∥B1C1,且FG=B1C1.
在平行四边形BCC1B1中,因为E是BC的中点,
所以EC∥B1C1,且EC=B1C1.
所以EC∥FG,且EC=FG.
所以四边形FECG是平行四边形.
所以FE∥GC.
又因为FE 平面A1C1CA,GC 平面A1C1CA,
所以EF∥平面A1C1CA.
21. 证明:(1)∵在棱长为2的正方体ACBD﹣A1C1B1D1中,AB∥A1B1,
A1B1 平面A1B1C,AB 平面A1B1C,
∴AB∥平面A1B1C.
(2)在棱长为2的正方体ACBD﹣A1C1B1D1中,
∵BC=AC,M是线段AB中点,∴CM⊥AB,
∵AA1⊥平面ABC,CM 平面ABC,则CM⊥AA1,
∵AB 平面ABB1A1,AA1 平面ABB1A1,
且AB∩AA1,∴CM⊥平面ABB1A1,
∵CM 平面MCC1,∴平面MCC1⊥平面ABB1A1.
解:(3)∵AB∥平面A1B1C,∴点M,点A到平面A1B1C的距离相等,
∴三棱锥M﹣A1B1C的体积:
===.
22.证明:(1)因为M为棱AC的中点,且AB=BC,所以BM⊥AC,
又因为ABC﹣A1B1C1是直三棱柱,所以AA1⊥平面ABC
因为BM 平面ABC,所以AA1⊥BM
又因为AC,A1A 平面ACC1A1且AC∩A1A=A,所以BM⊥平面ACC1A1
因为BM 平面BMN,所以:平面BMN⊥平面ACC1A1
(2)取BC的中点P,连接B1P和MP
因为M、P为棱AC、BC的中点,
所以 MP∥AB,且MP=AB,
因为ABC﹣A1B1C1是直三棱柱,
所以A1B1∥AB,A1B1=AB
因为N为棱A1B1的中点,
所以B1N∥BA,且B1N=BA;
所以B1N∥PM,且B1N=PM;
所以MNB1P是平行四边形,
所以MN∥PB1
又因为MN 平面BCC1B1,PB1 平面BCC1B1
所以MN∥平面BCC1B1
注意:也可以取C1B1的中点,同理用线面平行的判定定理证得) (说明:如用面面平行的性质定理证的话,一定先证线面平行,得到面面平行,再用面面平行的性质定理证得).
一、单选题
1.已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,侧视图为直角三角形,则该三棱锥的表面积为( )
A.4+ B.4 C.8+ D.6
2.设α,β为两个不重合的平面,能使α∥β成立的是( )
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α内有无数个点到β的距离相等
D.α,β垂直于同一平面
3.已知m,n是两条不重合的直线,α,β是两个不重合的平面,则下列命题中正确为( )
A.若m∥β,n⊥α,α⊥β,则m⊥n
B.若m⊥α,n⊥β,则α∥β
C.若m∥α,n∥β,α∥β,则m∥n
D.若α⊥β,α∩β=m,n β,m⊥n,则n⊥α
4.圆柱底面周长为4π,高为4,则它的体积为( )
A.4π B.8π C.12π D.16π
5.若一个圆锥的轴截面是边长为的等边三角形,则这个圆锥的表面积为( )
A.6π B.5π C.4π D.
6.如图,AB是圆的直径,PA⊥AC,PA⊥BC,C是圆上一点(不同于A,B),且PA=AC,则二面角P﹣BC﹣A的平面角为( )
A.∠PAC B.∠CPA C.∠PCA D.∠CAB
7.在下列条件中,可判断平面α与β平行的是( )
A.α⊥γ,且β⊥γ
B.m,n是两条异面直线,且m∥β,n∥β,m∥α,n∥α
C.m,n是α内的两条直线,且m∥β,n∥β
D.α内存在不共线的三点到β的距离相等
8.如图,在三棱柱ABC﹣A1B1C1中,A1A⊥底面ABC,AB⊥AC,A1A=AB=AC=2,那么三棱锥A1﹣ABC的体积是( )
A. B. C.4 D.8
9.如图,ABCD﹣A1B1C1D1为正方体,则以下结论:①BD∥平面CB1D1;②AC1⊥BD;③AC1⊥平面CB1D1.其中正确结论的个数是( )
A.0 B.1 C.2 D.3
10.如图所示的正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现沿SE,SF,EF把这个正方形折成一个四面体,使G1,G2,G3重合为点G,则有( )
A.SG⊥平面EFG B.EG⊥平面SEF C.GF⊥平面SEF D.SG⊥平面SEF
(多选)11.已知m,n是两条不重合的直线,α,β,γ是三个两两不重合的平面,则下列命题正确的是( )
A.若m⊥α,n⊥β,α∥β,则m∥n
B.若α⊥γ,β⊥γ,则α∥β
C.若m∥β,n∥β,m,n α,则α∥β
D.若n α,n⊥β,则α⊥β
(多选)12.已知m,n,l是三条直线,α是一个平面,下列命题不正确的是( )
A.若m∥l,n∥l,则m∥n B.若m⊥l,n⊥l,则m∥n
C.若m∥α,n∥α,则m∥n D.若m⊥α,n⊥α,则m∥n
二、填空题
13.三个平面两两垂直,它们的交线交于一点O,空间有一点P到三个面的距离分别为3、4、5,则OP的长为 .
14.设长方体的长、宽、高分别为3、2、1,其顶点都在同一个球面上,则该球的半径为 .
15.在底面为正方形的四棱锥P﹣ABCD中,PA⊥平面ABCD,PA=4,AB=3,则该四棱锥的外接球的表面积为 .
16.已知圆柱的两个底面的圆周在同一个球的球面上,圆柱的高和球半径均为2,则该圆柱的体积为 .
三、解答题
17.如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为BC,AC的中点,AB=BC.求证:
(1)A1B1∥平面DEC1;
(2)BE⊥C1E.
18.如图,四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,点F是PB的中点,点E是边BC上的任意一点.
(1)求证:AF⊥EF;
(2)求二面角A﹣PC﹣B的平面角的正弦值.
19.如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=120°,侧面PAB⊥底面ABCD,PB=2,AB=AC=PA=2.
(1)求证:BD⊥平面PAC;
(2)过AC的平面交PD于点M,若VM﹣PAC=,求三棱锥P﹣AMC的体积.
20.如图,在三棱柱ABC﹣A1B1C1中,B1C1⊥CC1,点E,F分别是BC,A1B1的中点,平面A1C1CA⊥平面BCC1B1.
(1)求证:B1C1⊥A1C;
(2)求证:EF∥平面A1C1CA.
21.如图,在棱长为2的正方体ACBD﹣A1C1B1D1中,M是线段AB上的动点.
(1)证明:AB∥平面A1B1C;
(2)若M是AB的中点,证明:平面MCC1⊥平面ABB1A1;
(3)求三棱锥M﹣A1B1C的体积.
22.如图,直三棱柱ABC﹣A1B1C1中,M,N分别为棱AC和A1B1的中点,且AB=BC.
(1)求证:平面BMN⊥平面ACC1A1;
(2)求证:MN∥平面BCC1B1.
参考答案与试题解析
一、单选题
1. 解:根据三视图转换为几何体的直观图:
该三棱锥是底面为腰长为2、底为的等腰三角形,
侧面分别是两个腰为2的等腰直角三角形和一个底为、高为的三角形,
如图所示:
所以该三棱锥的表面积为,
故选:A.
2. 解:对于A,α内有无数条直线与β平行,如两个相交平面,可以找出无数条平行于交线的直线,所以A错误;
对于B,α内有两条相交直线与β平行,根据两平面平行的判定定理知,α∥β,所以B正确;
对于C,α内有无数个点到β的距离相等,如两个相交平面,可以找出无数条直线平行于平面β,所以也能得出无数个点到平面β的距离相等,C错误;
对于D,当α、β垂直于同一个平面时,α与β也可以相交,所以D错误.
故选:B.
3. 解:由m,n是两条不重合的直线,α,β是两个不重合的平面,得:
在A中,若m∥β,n⊥α,α⊥β,则m与n相交、平行或异面,故A错误;
在B中,若m⊥α,n⊥β,则α与β相交或平行,故B错误;
在C中,若m∥α,n∥β,α∥β,则m与n相交、平行或异面,故C错误;
在D中,若α⊥β,α∩β=m,n β,m⊥n,
则由面面垂直的性质定理得n⊥α,故D正确.
故选:D.
4. 解:设圆柱底面半径为r,所以底面圆周长为2πr=4π,解得r=2;
又圆柱的高为4,所以它的体积为V=πr2h=π×22×4=16π.
故选:D.
5. 解:∵一个圆锥的轴截面是边长为的等边三角形,
设等边三角形的边长为2r,则2r=2,
则它的高为r,底面半径r=,
所以这个圆锥的表面积为π r2+πr 2r=6π,
故选:A.
6. 解:∵点C在以AB为直径的圆上,∴AC⊥BC,
又PA⊥BC,AC∩PA=A,AC、PA 平面PAC,
∴BC⊥平面PAC,
∴BC⊥PC,
∵AC⊥BC,∴∠PCA为二面角P﹣BC﹣A的平面角.
故选:C.
7. 解:A中:教室的墙角的两个平面都垂直底面,但是不平行,错误.
B中,利用平面与平面平行的判定,可得正确;
C中:如果这两条直线平行,那么平面α与β可能相交,所以C错误.
D中:如果这三个点在平面的两侧,满足不共线的三点到β的距离相等,这两个平面相交,B错误.
故选:B.
8. 解:∵AB⊥AC,AB=AC=2,
∴,且A1A⊥底面ABC,A1A=2,
∴.
故选:A.
9. 解:由正方体的性质得,BD∥B1D1,所以结合线面平行的判定定理可得:BD∥平面CB1D1;所以①正确.
由正方体的性质得 AC⊥BD,因为AC是AC1在底面ABCD内的射影,所以由三垂线定理可得:AC1⊥BD,所以②正确.
由正方体的性质得 BD∥B1D1,由②可得AC1⊥BD,所以AC1⊥B1D1,同理可得AC1⊥CB1,进而结合线面垂直的判定定理得到:AC1⊥平面CB1D1,所以③正确.
故选:D.
10. 解:如图所示
∵始终有 SG1⊥G1E,SG3⊥G3F,
∴SG⊥GE,SG⊥GF
又 GE∩GF=G
∴SG⊥平面 EFG.
故选:A.
11. 解:对于A,m⊥α,α∥β,则m⊥β,又n⊥β,则m∥n,故A正确;
对于B,由α⊥γ,β⊥γ,得α∥β或α与β相交,故B错误;
对于C,由m∥β,n∥β,m,n α,若m与n相交,则α∥β,若m∥n,则α可能平行β,也可能与β相交,故C错误;
对于D,由平面与平面垂直的判定,可得若n α,n⊥β,则α⊥β,故D正确.
故选:AD.
12. 解:对于A,若m∥l,n∥l,由平行公理可得m∥n,故A正确;
对于B,若m⊥l,n⊥l,则m∥n或m与n相交或m与n异面,故B错误;
对于C,若m∥α,n∥α,则m∥n或m与n相交或m与n异面,故C错误;
对于D,若m⊥α,n⊥α,由直线与平面垂直的性质可得m∥n,故D正确.
故选:BC.
二、填空题
13. 解:根据题意,过点P分别作三个平面的垂线,垂足分别为B、D、F,
∵三个平面两两垂直,
∴分别以PB、PD、PF为长、宽、高,作长方体OABC﹣EDPF,如图所示.
∵点P到三个面的距离分别为3、4、5,
∴长方体的对角线长为=,
即OP的长为.
故答案为:5
14. 解:由长方体的对角线等于其外接球的直径2R可得:(2R)2=32+22+12,解得:R=,
故答案为:.
15. 解:底面为正方形的四棱锥P﹣ABCD中,PA⊥平面ABCD,PA=4,AB=3,
如图所示:
设外接球的半径为R,
所以(2R)2=42+32+32=34,
解得,
所以.
故答案为:34π.
16. 解:设圆柱上底面圆的半径为r,
则根据题意得r2+1=4,∴r2=3,
∴该圆柱的体积为V=3π 2=6π.
故答案为:6π.
三、解答题
17. 证明:(1)∵在直三棱柱ABC﹣A1B1C1中,D,E分别为BC,AC的中点,
∴DE∥AB,AB∥A1B1,∴DE∥A1B1,
∵DE 平面DEC1,A1B1 平面DEC1,
∴A1B1∥平面DEC1.
解:(2)∵在直三棱柱ABC﹣A1B1C1中,E是AC的中点,AB=BC.
∴BE⊥AC,
∵直三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,BE 平面ABC,
∴BE⊥AA1,
又AA1∩AC=A,∴BE⊥平面ACC1A1,
∵C1E 平面ACC1A1,∴BE⊥C1E.
18. (1)证明:∵四边形ABCD是正方形,△PAB与△PAD均是以A为直角顶点的等腰直角三角形,
∴PA⊥AD,PA⊥AB,又AD∩AB=A,AB⊥BC,
∴PA⊥平面ABCD,又BC 面ABCD,∴PA⊥BC,
∵AB∩PA=A,∴BC⊥面PAB,
∴BC⊥AF,
∵△PAB是以A为直角顶点的等腰直角三角形,F是PB中点,
∴AF⊥PB,
又PB∩BC=B,∴AF⊥平面PBC,
∵EF 平面PBC,∴AF⊥EF.
(2)解:以A为原点,AD为x轴,AB为y轴,P为z轴,
建立空间直角坐标系,
设AB=1,则A(0,0,0),B(0,1,0),C(1,1,0),P(0,0,1),
=(0,0,1),=(1,1,0),
设平面APC的法向量=(x,y,z),
则,取x=1,得=(1,﹣1,0),
=(0,1,﹣1),=(1,1,﹣1),
设平面PBC的法向量=(a,b,c),
则,取b=1,得=(0,1,1),
|cos<>|=||=,
∴<>=60°,又sin60°=,
∴二面角A﹣PC﹣B的平面角的正弦值为.
19. 证明:(1)由题意,底面ABCD是菱形,且AB=AC=2,∴BD⊥AC,
在△PAB中,∵AB=PA=2,,∴PA2+AB2=PB2,
即∠PAB=90°,∴PA⊥AB,
又平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,PA 平面PAB,
∴PA⊥平面ABCD,而BD 平面ABCD,则PA⊥BD,
又PA∩AC=A,∴BD⊥平面PAC;
解:(2)由(1)知:PA⊥平面ABCD,
∴==,
而VM﹣PAC=VP﹣AMC,且,
∴.
20. 证明:(1)因为BC1⊥C1C,又平面A1C1CA⊥平面BCC1B1,
且平面A1C1CA∩平面BCC1B1=C1C,
所以BC1⊥平面ACC1A1.
又因为A1C 平面A1C1CA,
所以BC1⊥A1C.
(2)取A1C1中点G,连FG,连GC,如图所示:
在△A1B1C1中,因为F,G分别是A1B1,A1C1中点,
所以FG∥B1C1,且FG=B1C1.
在平行四边形BCC1B1中,因为E是BC的中点,
所以EC∥B1C1,且EC=B1C1.
所以EC∥FG,且EC=FG.
所以四边形FECG是平行四边形.
所以FE∥GC.
又因为FE 平面A1C1CA,GC 平面A1C1CA,
所以EF∥平面A1C1CA.
21. 证明:(1)∵在棱长为2的正方体ACBD﹣A1C1B1D1中,AB∥A1B1,
A1B1 平面A1B1C,AB 平面A1B1C,
∴AB∥平面A1B1C.
(2)在棱长为2的正方体ACBD﹣A1C1B1D1中,
∵BC=AC,M是线段AB中点,∴CM⊥AB,
∵AA1⊥平面ABC,CM 平面ABC,则CM⊥AA1,
∵AB 平面ABB1A1,AA1 平面ABB1A1,
且AB∩AA1,∴CM⊥平面ABB1A1,
∵CM 平面MCC1,∴平面MCC1⊥平面ABB1A1.
解:(3)∵AB∥平面A1B1C,∴点M,点A到平面A1B1C的距离相等,
∴三棱锥M﹣A1B1C的体积:
===.
22.证明:(1)因为M为棱AC的中点,且AB=BC,所以BM⊥AC,
又因为ABC﹣A1B1C1是直三棱柱,所以AA1⊥平面ABC
因为BM 平面ABC,所以AA1⊥BM
又因为AC,A1A 平面ACC1A1且AC∩A1A=A,所以BM⊥平面ACC1A1
因为BM 平面BMN,所以:平面BMN⊥平面ACC1A1
(2)取BC的中点P,连接B1P和MP
因为M、P为棱AC、BC的中点,
所以 MP∥AB,且MP=AB,
因为ABC﹣A1B1C1是直三棱柱,
所以A1B1∥AB,A1B1=AB
因为N为棱A1B1的中点,
所以B1N∥BA,且B1N=BA;
所以B1N∥PM,且B1N=PM;
所以MNB1P是平行四边形,
所以MN∥PB1
又因为MN 平面BCC1B1,PB1 平面BCC1B1
所以MN∥平面BCC1B1
注意:也可以取C1B1的中点,同理用线面平行的判定定理证得) (说明:如用面面平行的性质定理证的话,一定先证线面平行,得到面面平行,再用面面平行的性质定理证得).
同课章节目录
