2.3 二次函数与一元二次方程、不等式(第一课时)课件(共29张PPT)
文档属性
| 名称 | 2.3 二次函数与一元二次方程、不等式(第一课时)课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
2.3 二次函数与
一元二次方程、不等式
(第一课时)
人教A版2019必修第一册
学习目标
1. 理解一元二次不等式的概念,掌握一元二次不等式的解法;
2. 理解一元二次不等式、一元二次函数及一元二次方程的关系;
3. 理解含参不等式的解法。
情景导入
问题 园艺师打算在绿地上用栅栏围一个矩形区域种植花卉.若栅栏的长度是24m,围成的矩形区域的面积要大于20 m2,则这个矩形的边长为多少米?
设这个矩形的一条边长为xcm,则另一条边长为(12-x)m,
由题意,得
(12-x)x>20,其中x∈{x|0整理得
x2-12x+20<0, x∈{x|0求得上述不等式的解集,即可得到问题的答案.
新知讲解
一般地,我们把只含有一个未知数,并且未知数的最高次是2的不等式,称为一元二次不等式.
一元二次不等式的一般形式是:
注:若无a≠0这个条件,则该不等式不一定是一元二次不等式,需对a是否为零展开讨论.
新知讲解
在初中,我们学习了从一次函数的观点看一元一次方程、一元一次不等式的思想方法.类似地,能否从二次函数的观点看一元二次不等式,进而得到一元二次不等式的求解方法呢?
步骤:1.做出函数的图像;
2.求出图像与x轴交点的横坐标;(函数的零点)
3.观察图像位于x轴上方(或下方)所对应的x取值范围.
注:使得 成立的实数x(方程 的解)即为二次函数 的零点.
新知讲解
观察一元二次不等式x2-12x+20<0与二次函数y=x2-12x+20间有何关系?
二次函数y=x2-12x+20 的两个零点x1=2,x2=10将x轴分成三段.
当x<2 时,y>0,即x2-12x+20>0;
当2当x>10时,y>0,即x2-12x+20>0;
故一元二次不等式x2-12x+20<0
的解集是{x|2<x<10}.
新知讲解
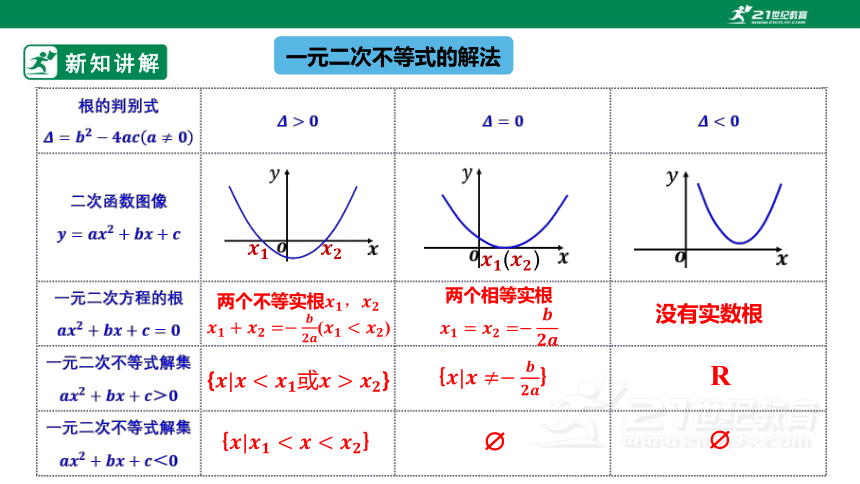
一元二次不等式的解法
()
两个不等实根
()
两个相等实根
没有实数根
{}
{}
R
{}
典例分析
【例1】(1)求不等式x2-5x+6>0的解集.
【解析】对于方程x2-5x+6>0,因为Δ>0,
故有两个不等的实数根,解得x1=2,x2=3 .
画出二次函数y=x2-5x+6的大致图象,
结合图象得不等式x2-5x+6>0
的解集为:
一元二次不等式的解法
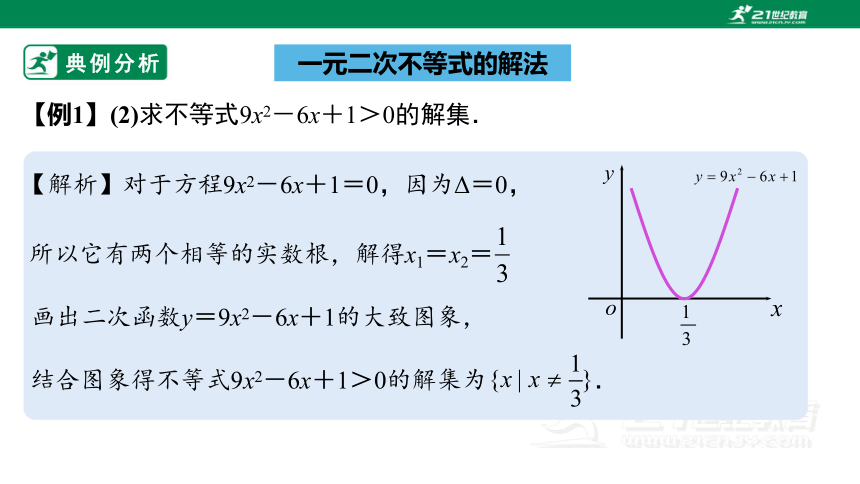
【例1】(2)求不等式9x2-6x+1>0的解集.
【解析】对于方程9x2-6x+1=0,因为Δ=0,
画出二次函数y=9x2-6x+1的大致图象,
结合图象得不等式9x2-6x+1>0的解集为 .
所以它有两个相等的实数根,解得x1=x2=
典例分析
一元二次不等式的解法
【例1】(3)求不等式-x2+2x-3>0的解集.
【解析】不等式可化为x2-2x+3<0,因为 <0
所以方程x2-2x+3=0无实数根
画出二次函数y=x2-2x+3的大致图象,
结合图象得不等式x2-2x+3<0的解集为:
典例分析
一元二次不等式的解法
解一元二次不等式的过程
将原不等式化成的形式
计算的值
方程有两个不等实根( )
原不等式的解集为
{|}
方程有两个相等实根( )
原不等式的解集为
{|}
方程
没有实根
原不等式的解集为
R
方法归纳
变式训练
【变式1】 解不等式:
(1)2x2-3x-2>0; (2)-3x2+6x-2>0;
(3)4x2-4x+1≤0; (4)x2-2x+2>0.
一元二次不等式的解法
图①
解:(1)对于方程2x2-3x-2=0,因为Δ>0,所以它有两个不相等的实数根.
变式训练
一元二次不等式的解法
(2)原不等式可化为3x2-6x+2<0.
对于方程3x2-6x+2=0,
因为Δ=36-4×3×2=12>0,
所以它有两个不相等的实数根,
图②
变式训练
一元二次不等式的解法
图③
变式训练
一元二次不等式的解法
(4)对于方程x2-2x+2=0,因为Δ<0,所以方程x2-2x+2=0无实数根.
画出二次函数y=x2-2x+2的图象(图④),结合图象得不等式x2-2x+2>0的解集为R.
图④
变式训练
一元二次不等式的解法
一元二次不等式、一元二次方程与二次函数间的关系
典例分析
变式训练
一元二次不等式、一元二次方程与二次函数间的关系
典例分析
【例3】 解关于x的不等式x2-2ax-8a2<0.
解:不等式x2-2ax-8a2<0可化为(x+2a)(x-4a)<0,
方程x2-2ax-8a2=0的两根为x1=-2a,x2=4a.
当-2a=4a,即a=0时,不等式即为x2<0,解集为 ;
当-2a>4a,即a<0时,得4a当-2a<4a,即a>0时,得-2a综上所述,当a=0时,原不等式的解集为 ;
当a<0时,原不等式的解集为{x|4a当a>0时,原不等式的解集为{x|-2a解含参数的一元二次不等式
【变式3】 解关于x的不等式ax2-(a+1)x+1>0.
变式训练
解含参数的一元二次不等式
变式训练
解含参数的一元二次不等式
当堂检测
B
解析:因为2x+3-x2>0,
所以(x-3)(x+1)<0,
所以-1所以不等式的解集为{x|-1当堂检测
C
当堂检测
当堂检测
4.二次函数y=ax2+bx+c(x∈R)的部分对应值如表:
x -3 -2 -1 0 1 2 3 4
y 6 0 -4 -6 -6 -4 0 6
则不等式ax2+bx+c>0的解集是 .
解析:由表知当x=-2,或x=3时,y=0,
所以二次函数y=ax2+bx+c可化为y=a(x+2)(x-3).
又因为当x=1时,y=-6,
所以a=1.
所以不等式ax2+bx+c>0的解集为{x|x<-2或x>3}.
答案:{x|x<-2或x>3}
当堂检测
5.求不等式12x2-ax>a2(a∈R)的解集.
课堂小结
1.化标准
2.计算判别式
将原不等式化成 ax2+bx+c>0(a>0) 的形式
计算 =b2-4ac 的值
方程 ax2+bx+c=0 有
两个不相等的实数根,
解得 x1,x2 (x1方程 ax2+bx+c=0 有两个相等的实数根,解得 x1=x2=-
方程 ax2+bx+c=0 没有实数根
原不等式的解集为{ x | xx2 }
原不等式的解集为{ x | x≠- }
原不等式的解集为 R
>0
=0
<0
4.口诀(大于取两边,小于取中间)
3.求根(因式分解、求根公式)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.3 二次函数与
一元二次方程、不等式
(第一课时)
人教A版2019必修第一册
学习目标
1. 理解一元二次不等式的概念,掌握一元二次不等式的解法;
2. 理解一元二次不等式、一元二次函数及一元二次方程的关系;
3. 理解含参不等式的解法。
情景导入
问题 园艺师打算在绿地上用栅栏围一个矩形区域种植花卉.若栅栏的长度是24m,围成的矩形区域的面积要大于20 m2,则这个矩形的边长为多少米?
设这个矩形的一条边长为xcm,则另一条边长为(12-x)m,
由题意,得
(12-x)x>20,其中x∈{x|0
x2-12x+20<0, x∈{x|0
新知讲解
一般地,我们把只含有一个未知数,并且未知数的最高次是2的不等式,称为一元二次不等式.
一元二次不等式的一般形式是:
注:若无a≠0这个条件,则该不等式不一定是一元二次不等式,需对a是否为零展开讨论.
新知讲解
在初中,我们学习了从一次函数的观点看一元一次方程、一元一次不等式的思想方法.类似地,能否从二次函数的观点看一元二次不等式,进而得到一元二次不等式的求解方法呢?
步骤:1.做出函数的图像;
2.求出图像与x轴交点的横坐标;(函数的零点)
3.观察图像位于x轴上方(或下方)所对应的x取值范围.
注:使得 成立的实数x(方程 的解)即为二次函数 的零点.
新知讲解
观察一元二次不等式x2-12x+20<0与二次函数y=x2-12x+20间有何关系?
二次函数y=x2-12x+20 的两个零点x1=2,x2=10将x轴分成三段.
当x<2 时,y>0,即x2-12x+20>0;
当2
故一元二次不等式x2-12x+20<0
的解集是{x|2<x<10}.
新知讲解
一元二次不等式的解法
()
两个不等实根
()
两个相等实根
没有实数根
{}
{}
R
{}
典例分析
【例1】(1)求不等式x2-5x+6>0的解集.
【解析】对于方程x2-5x+6>0,因为Δ>0,
故有两个不等的实数根,解得x1=2,x2=3 .
画出二次函数y=x2-5x+6的大致图象,
结合图象得不等式x2-5x+6>0
的解集为:
一元二次不等式的解法
【例1】(2)求不等式9x2-6x+1>0的解集.
【解析】对于方程9x2-6x+1=0,因为Δ=0,
画出二次函数y=9x2-6x+1的大致图象,
结合图象得不等式9x2-6x+1>0的解集为 .
所以它有两个相等的实数根,解得x1=x2=
典例分析
一元二次不等式的解法
【例1】(3)求不等式-x2+2x-3>0的解集.
【解析】不等式可化为x2-2x+3<0,因为 <0
所以方程x2-2x+3=0无实数根
画出二次函数y=x2-2x+3的大致图象,
结合图象得不等式x2-2x+3<0的解集为:
典例分析
一元二次不等式的解法
解一元二次不等式的过程
将原不等式化成的形式
计算的值
方程有两个不等实根( )
原不等式的解集为
{|}
方程有两个相等实根( )
原不等式的解集为
{|}
方程
没有实根
原不等式的解集为
R
方法归纳
变式训练
【变式1】 解不等式:
(1)2x2-3x-2>0; (2)-3x2+6x-2>0;
(3)4x2-4x+1≤0; (4)x2-2x+2>0.
一元二次不等式的解法
图①
解:(1)对于方程2x2-3x-2=0,因为Δ>0,所以它有两个不相等的实数根.
变式训练
一元二次不等式的解法
(2)原不等式可化为3x2-6x+2<0.
对于方程3x2-6x+2=0,
因为Δ=36-4×3×2=12>0,
所以它有两个不相等的实数根,
图②
变式训练
一元二次不等式的解法
图③
变式训练
一元二次不等式的解法
(4)对于方程x2-2x+2=0,因为Δ<0,所以方程x2-2x+2=0无实数根.
画出二次函数y=x2-2x+2的图象(图④),结合图象得不等式x2-2x+2>0的解集为R.
图④
变式训练
一元二次不等式的解法
一元二次不等式、一元二次方程与二次函数间的关系
典例分析
变式训练
一元二次不等式、一元二次方程与二次函数间的关系
典例分析
【例3】 解关于x的不等式x2-2ax-8a2<0.
解:不等式x2-2ax-8a2<0可化为(x+2a)(x-4a)<0,
方程x2-2ax-8a2=0的两根为x1=-2a,x2=4a.
当-2a=4a,即a=0时,不等式即为x2<0,解集为 ;
当-2a>4a,即a<0时,得4a
当a<0时,原不等式的解集为{x|4a
【变式3】 解关于x的不等式ax2-(a+1)x+1>0.
变式训练
解含参数的一元二次不等式
变式训练
解含参数的一元二次不等式
当堂检测
B
解析:因为2x+3-x2>0,
所以(x-3)(x+1)<0,
所以-1
C
当堂检测
当堂检测
4.二次函数y=ax2+bx+c(x∈R)的部分对应值如表:
x -3 -2 -1 0 1 2 3 4
y 6 0 -4 -6 -6 -4 0 6
则不等式ax2+bx+c>0的解集是 .
解析:由表知当x=-2,或x=3时,y=0,
所以二次函数y=ax2+bx+c可化为y=a(x+2)(x-3).
又因为当x=1时,y=-6,
所以a=1.
所以不等式ax2+bx+c>0的解集为{x|x<-2或x>3}.
答案:{x|x<-2或x>3}
当堂检测
5.求不等式12x2-ax>a2(a∈R)的解集.
课堂小结
1.化标准
2.计算判别式
将原不等式化成 ax2+bx+c>0(a>0) 的形式
计算 =b2-4ac 的值
方程 ax2+bx+c=0 有
两个不相等的实数根,
解得 x1,x2 (x1
方程 ax2+bx+c=0 没有实数根
原不等式的解集为{ x | x
原不等式的解集为{ x | x≠- }
原不等式的解集为 R
>0
=0
<0
4.口诀(大于取两边,小于取中间)
3.求根(因式分解、求根公式)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
