【沪教版】数学三年级第一学期第五单元《面积》(表格式教案)
文档属性
| 名称 | 【沪教版】数学三年级第一学期第五单元《面积》(表格式教案) |

|
|
| 格式 | docx | ||
| 文件大小 | 140.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 00:00:00 | ||
图片预览

文档简介
面积
【教学内容】P60
【教学目标】
1.结合具体实例和画图活动,理解认识图形面积的含义。
2.通过目测、重叠、数方格的方法来理解面积的大小。
3.培养学生的抽象概括能力,感知计算图形的面积是有趣的和有用的,建立初步的空间概念。
【教学重点】
通过探究多种方法比较图形面积大小的过程,学会用方格的多少表示面积的大小。
【教学难点】
灵活、准确地计数方格(初步接触凑整的思想)。
【教学资源】
垫板、小正方形纸片、圆形纸片、剪刀、方格纸、练习纸
【教学过程】
教学环节 师生活动 设计说明/评价关注点
创设情境激发兴趣 1、情境引入:同学们做好了上课的准备了吗?看看,你们的桌面上有些什么? 师:摸一摸课本、练习本、橡皮这些物体的表面。 2、认识生活中物体的表面 问:你能再找一找、摸一摸身边其它物体的表面吗? 3、感知平面图形的面 师:这4个平面图形中,哪个图形的面最大?你们是不是直接用眼睛观察出来的? 小结:用眼睛直接观察,比较面的大小的方法叫做观察法。 【板书】观察法 4、揭示课题——面积 小结:通过刚才的学习,我们知道了物体的表面是有大小的,平面图形的表面也是有大小的。我们把平面图形的大小称作为他们的面积。 【板书】平面图形的大小就是他们的面积。 以谈话的形式,以亲身的感官体验进入本节课的学习,激发学生的学习兴趣,感知物体的面有大有小,逐步理解面积的含义,为“面积”概念的引入创造了条件,直观地让学生理解面积的含义。/初步理解面积的概念。
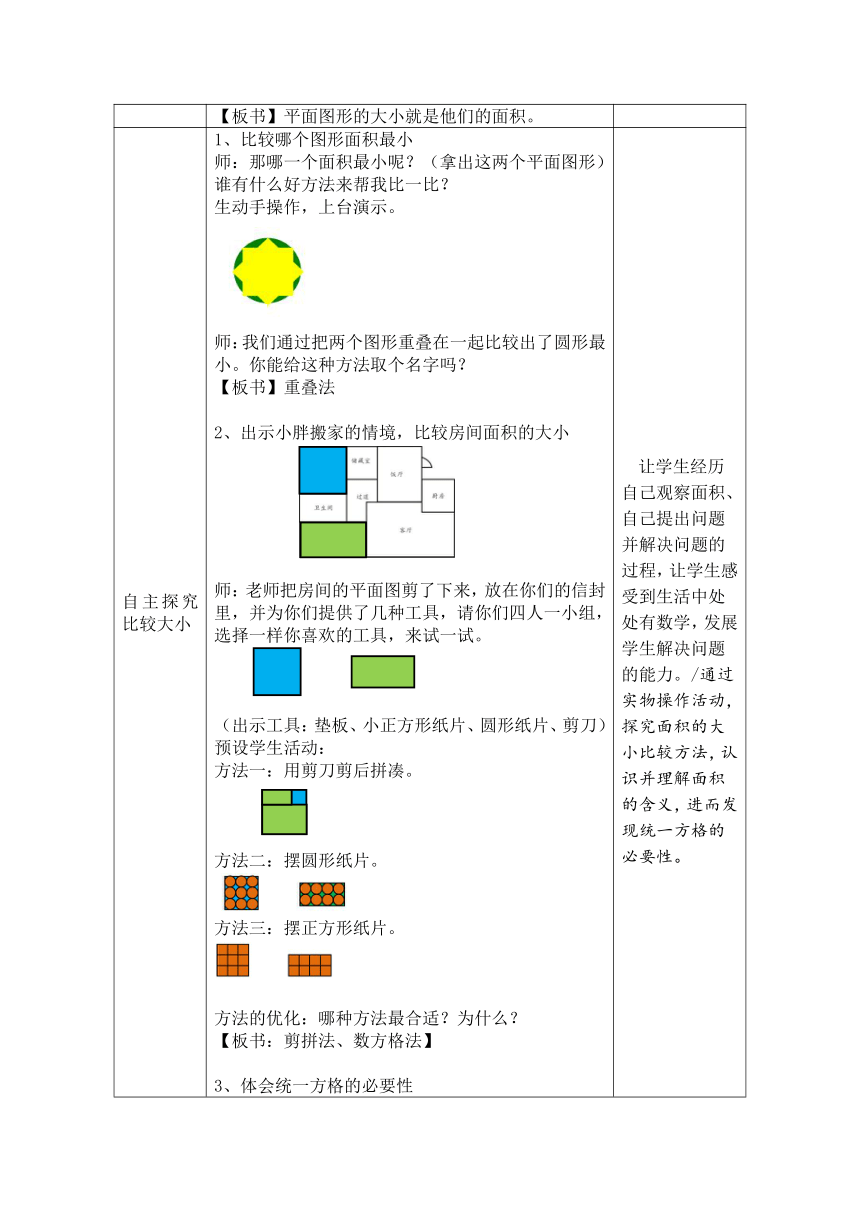
自主探究比较大小 1、比较哪个图形面积最小 师:那哪一个面积最小呢?(拿出这两个平面图形)谁有什么好方法来帮我比一比? 生动手操作,上台演示。 师:我们通过把两个图形重叠在一起比较出了圆形最小。你能给这种方法取个名字吗? 【板书】重叠法 2、出示小胖搬家的情境,比较房间面积的大小 师:老师把房间的平面图剪了下来,放在你们的信封里,并为你们提供了几种工具,请你们四人一小组,选择一样你喜欢的工具,来试一试。 (出示工具:垫板、小正方形纸片、圆形纸片、剪刀) 预设学生活动: 方法一:用剪刀剪后拼凑。 方法二:摆圆形纸片。 方法三:摆正方形纸片。 方法的优化:哪种方法最合适?为什么? 【板书:剪拼法、数方格法】 3、体会统一方格的必要性 师:现在大家会用数方格法来表示平面图形的面积了,方格数多,面积就大,方格数少,面积就小,你们同意吗? 那要是摆9个方格的图形和摆6个方格的图形比,哪个面积大? 那摆9个方格的图形和摆4个方格的图形比,哪个面积大? 师:测量的时候,要注意什么呢? 小结:要统一方格的标准,用一样的格子才能去比较。 【板书】(统一标准) 4、介绍工具:方格纸 师:为了测量标准的统一,数学家把边长为1cm的小正方形拼在一起,成为了一张方格纸。 教师小结并演示:要想知道哪个图形面积大,可以把透明方格纸放上去,数一数各个图形中的方格数来比较。在放透明方格纸时要注意,尽量让不完整的格子少出现。 5、用方格纸测量图形的大小 师:请大家利用透明方格纸数一数,这两个图形的面积是多少?小组讨论一下,怎么数最快?(正方形36格,长方形32格) 独立练习后讨论数方格的方法。 预设: 生1:我发现每一行都有6格,有这样的6行, 6×6=36,所以正方形的面积就是36格。 生2:我发现每一行都有8格,有这样的4行, 8×4=32,所以长方形的面积就是32格。 小结:借用透明方格纸知道图形的面积有多大是一个好方法。在这里,我们不仅仅可以用一格一格数的方法,还可以用乘法来计算。 让学生经历自己观察面积、自己提出问题并解决问题的过程,让学生感受到生活中处处有数学,发展学生解决问题的能力。/通过实物操作活动,探究面积的大小比较方法,认识并理解面积的含义,进而发现统一方格的必要性。 让学生掌握观察法、剪拼法、重叠法、数方格法等测量面积的方法,有利于学生灵活、准确地比较面积。通过借助方格纸测量图形面积的大小,形成对面积的量化。/掌握借助方格纸测量图形大小的操作方法,理解数方格数表示面积大小的方法。
实践体验巩固深化 1、红、黄、绿图形的面积各占几格? 学生动手操作后集体交流,重点交流绿色图形的面积大小。 【板书】不规则→规则 不满一格→拼凑为整格 小结:三个图形都占20格,方格数相同,面积相同,形状不同。 2、比较两个轴对称图形的面积大小 学生同桌合作,计算面积后再一起比较大小。 根据学生的思维特点设计一系列基本练习和变式练习,特别是让学生掌握“将不规则图形转变成规则图形”以及“拼凑为整”的思想,让学生在小组合作的过程中兴趣盎然地参与到练习中。/掌握用数方格法计算不规则图形的面积大小,掌握“拼凑为整”的思想。
交流总结 1、什么是面积? 2、比较面积大小可以用哪些方法呢? 3、有些什么好经验可以分享? 生交流总结。 梳理回顾全课主要知识点,理解面积的概念,知道比较面积大小可用直接比较或间接比较等多种方法。/能说出面积的含义,能运用多种方法比较两个图形的面积大小,能解决生活中关于面积的实际问题。
【教学内容】P60
【教学目标】
1.结合具体实例和画图活动,理解认识图形面积的含义。
2.通过目测、重叠、数方格的方法来理解面积的大小。
3.培养学生的抽象概括能力,感知计算图形的面积是有趣的和有用的,建立初步的空间概念。
【教学重点】
通过探究多种方法比较图形面积大小的过程,学会用方格的多少表示面积的大小。
【教学难点】
灵活、准确地计数方格(初步接触凑整的思想)。
【教学资源】
垫板、小正方形纸片、圆形纸片、剪刀、方格纸、练习纸
【教学过程】
教学环节 师生活动 设计说明/评价关注点
创设情境激发兴趣 1、情境引入:同学们做好了上课的准备了吗?看看,你们的桌面上有些什么? 师:摸一摸课本、练习本、橡皮这些物体的表面。 2、认识生活中物体的表面 问:你能再找一找、摸一摸身边其它物体的表面吗? 3、感知平面图形的面 师:这4个平面图形中,哪个图形的面最大?你们是不是直接用眼睛观察出来的? 小结:用眼睛直接观察,比较面的大小的方法叫做观察法。 【板书】观察法 4、揭示课题——面积 小结:通过刚才的学习,我们知道了物体的表面是有大小的,平面图形的表面也是有大小的。我们把平面图形的大小称作为他们的面积。 【板书】平面图形的大小就是他们的面积。 以谈话的形式,以亲身的感官体验进入本节课的学习,激发学生的学习兴趣,感知物体的面有大有小,逐步理解面积的含义,为“面积”概念的引入创造了条件,直观地让学生理解面积的含义。/初步理解面积的概念。
自主探究比较大小 1、比较哪个图形面积最小 师:那哪一个面积最小呢?(拿出这两个平面图形)谁有什么好方法来帮我比一比? 生动手操作,上台演示。 师:我们通过把两个图形重叠在一起比较出了圆形最小。你能给这种方法取个名字吗? 【板书】重叠法 2、出示小胖搬家的情境,比较房间面积的大小 师:老师把房间的平面图剪了下来,放在你们的信封里,并为你们提供了几种工具,请你们四人一小组,选择一样你喜欢的工具,来试一试。 (出示工具:垫板、小正方形纸片、圆形纸片、剪刀) 预设学生活动: 方法一:用剪刀剪后拼凑。 方法二:摆圆形纸片。 方法三:摆正方形纸片。 方法的优化:哪种方法最合适?为什么? 【板书:剪拼法、数方格法】 3、体会统一方格的必要性 师:现在大家会用数方格法来表示平面图形的面积了,方格数多,面积就大,方格数少,面积就小,你们同意吗? 那要是摆9个方格的图形和摆6个方格的图形比,哪个面积大? 那摆9个方格的图形和摆4个方格的图形比,哪个面积大? 师:测量的时候,要注意什么呢? 小结:要统一方格的标准,用一样的格子才能去比较。 【板书】(统一标准) 4、介绍工具:方格纸 师:为了测量标准的统一,数学家把边长为1cm的小正方形拼在一起,成为了一张方格纸。 教师小结并演示:要想知道哪个图形面积大,可以把透明方格纸放上去,数一数各个图形中的方格数来比较。在放透明方格纸时要注意,尽量让不完整的格子少出现。 5、用方格纸测量图形的大小 师:请大家利用透明方格纸数一数,这两个图形的面积是多少?小组讨论一下,怎么数最快?(正方形36格,长方形32格) 独立练习后讨论数方格的方法。 预设: 生1:我发现每一行都有6格,有这样的6行, 6×6=36,所以正方形的面积就是36格。 生2:我发现每一行都有8格,有这样的4行, 8×4=32,所以长方形的面积就是32格。 小结:借用透明方格纸知道图形的面积有多大是一个好方法。在这里,我们不仅仅可以用一格一格数的方法,还可以用乘法来计算。 让学生经历自己观察面积、自己提出问题并解决问题的过程,让学生感受到生活中处处有数学,发展学生解决问题的能力。/通过实物操作活动,探究面积的大小比较方法,认识并理解面积的含义,进而发现统一方格的必要性。 让学生掌握观察法、剪拼法、重叠法、数方格法等测量面积的方法,有利于学生灵活、准确地比较面积。通过借助方格纸测量图形面积的大小,形成对面积的量化。/掌握借助方格纸测量图形大小的操作方法,理解数方格数表示面积大小的方法。
实践体验巩固深化 1、红、黄、绿图形的面积各占几格? 学生动手操作后集体交流,重点交流绿色图形的面积大小。 【板书】不规则→规则 不满一格→拼凑为整格 小结:三个图形都占20格,方格数相同,面积相同,形状不同。 2、比较两个轴对称图形的面积大小 学生同桌合作,计算面积后再一起比较大小。 根据学生的思维特点设计一系列基本练习和变式练习,特别是让学生掌握“将不规则图形转变成规则图形”以及“拼凑为整”的思想,让学生在小组合作的过程中兴趣盎然地参与到练习中。/掌握用数方格法计算不规则图形的面积大小,掌握“拼凑为整”的思想。
交流总结 1、什么是面积? 2、比较面积大小可以用哪些方法呢? 3、有些什么好经验可以分享? 生交流总结。 梳理回顾全课主要知识点,理解面积的概念,知道比较面积大小可用直接比较或间接比较等多种方法。/能说出面积的含义,能运用多种方法比较两个图形的面积大小,能解决生活中关于面积的实际问题。
同课章节目录
- 一、复习与提高
- 小复习
- 连乘、连除
- 正方形组成的图形——多连块
- 二、用一位数乘
- 乘整十数、整百数
- 看图列式
- 一位数与两位数相乘
- 一位数与三位数相乘
- 小练习(1)
- 三、时间的初步认识(三)
- 年、月、日
- 平年和闰年
- 制作年历
- 小练习(2)
- 四、用一位数除
- 整十数、整百数的除法
- 两位数被一位数除
- 三位数被一位数除
- 除法的应用
- 单价、数量、总价
- 小练习(3)
- 五、几何小实践
- 千米的认识
- 米与厘米
- 分米的认识
- 轴对称图形
- 三角形的分类(2)
- 面积
- 正方形与长方形的面积
- 平方米
- 六、整理与提高
- 乘乘除除
- 解决问题
- 图形的拼嵌
- 它们有多大
- 计算小胖家的面积
- 数学广场——植树问题
- 数学广场——周期问题
- 数学广场——流程图(2)
