北师大版六年级下册数学 圆柱的体积(课件)(共21张PPT)
文档属性
| 名称 | 北师大版六年级下册数学 圆柱的体积(课件)(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 46.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
圆柱的体积(1)
北师大版·六年级下册
要知道需要柱子需要多少木材,就需要计算柱子的体积,而柱子是圆柱形,怎样计算圆柱的体积呢?
探究新知
什么是圆柱的
体积呢?
圆柱所占空间的大小是圆柱的体积。
a
b
h
a
a
a
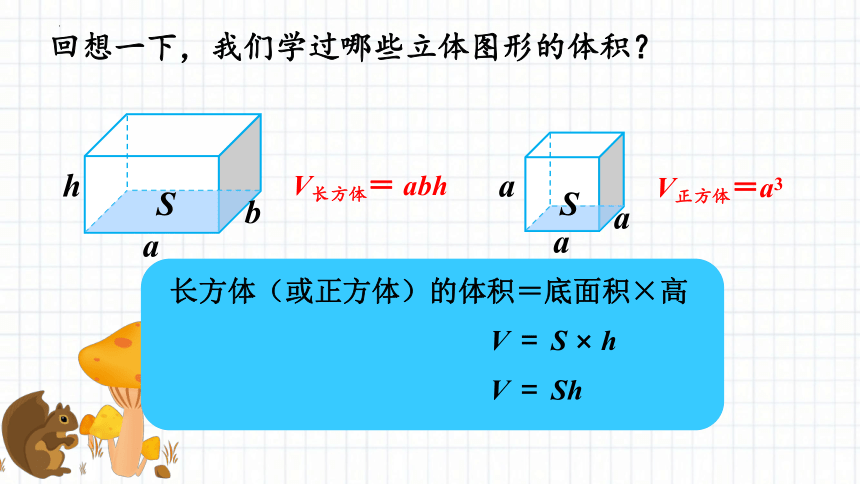
回想一下,我们学过哪些立体图形的体积?
V长方体= abh
V正方体=a3
长方体(或正方体)的体积=底面积×高
V = S × h
V = Sh
S
S
a
b
h
a
a
a
S
S
V = Sh
V = Sh
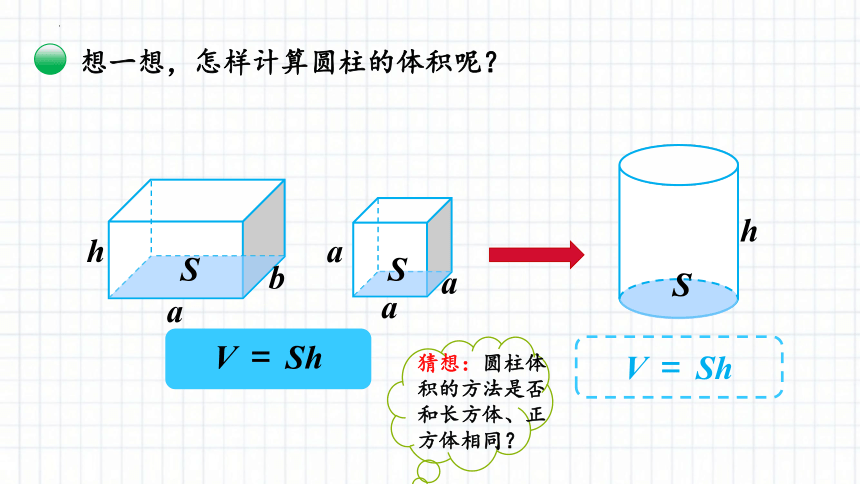
想一想,怎样计算圆柱的体积呢?
S
h
猜想:圆柱体积的方法是否和长方体、正方体相同?
圆柱的体积=底面积×高
尝试验证你的猜想,并与同伴交流。
通过叠硬币,我们发现硬币的
( )是固定的,每增加一枚硬币,( )就增加一些,( )也随之增大。
方法一:堆硬币法
由此可见:
底面积
高
体积
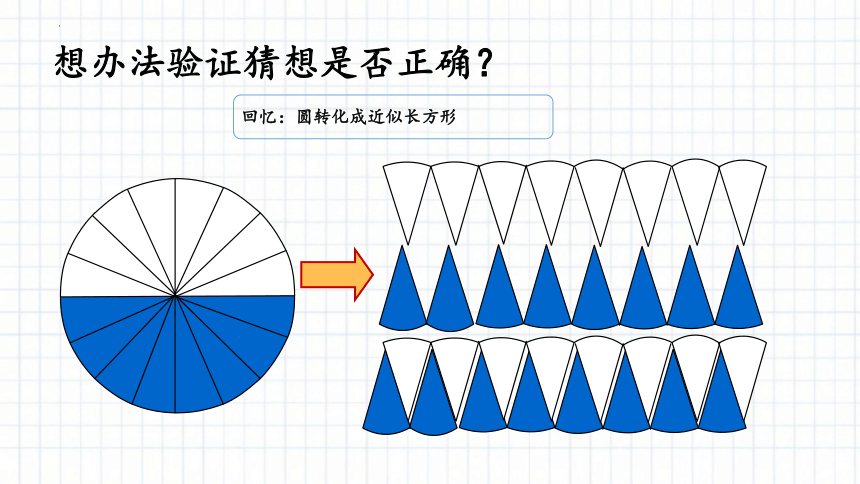
想办法验证猜想是否正确?
想办法验证猜想是否正确?
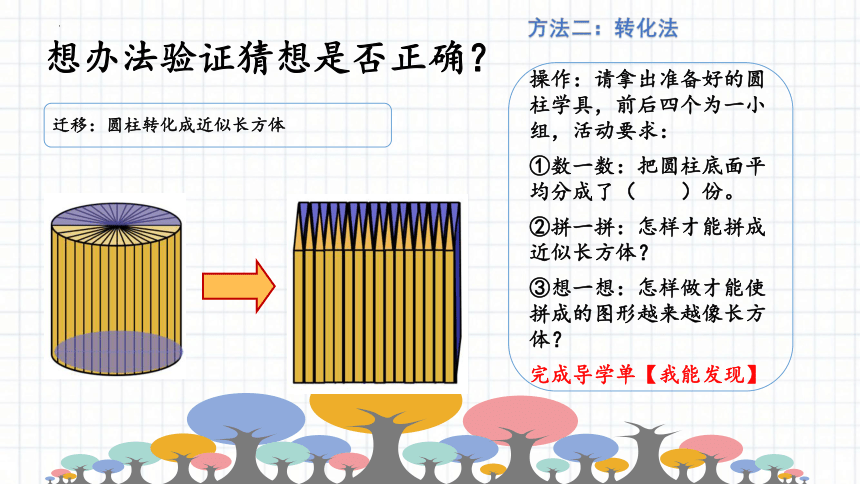
方法二:转化法
想办法验证猜想是否正确?
方法二:转化法
切开后拼成的物体会有什么变化?什么没变?
如果用V表示圆柱的体积,S表示圆柱的底面积,
h表示圆柱的高,那么圆柱的体积计算公式可以表示为
圆柱的体积
底面积
高
=
×
V = Sh
S
h
思考还能怎样计算圆柱的体积?
圆柱底面积
长方体底面积
长方体的高
圆柱的高
底面圆周长的一半
底面圆的半径
迁移:圆柱转化成近似长方体
V = πr2h
想办法验证猜想是否正确?
方法二:转化法
完成导学单:
V =π(d÷2)2h
V = πr2h
V =π(C÷π÷2)2h
(1)已知底面半径r和高h,怎样求圆柱的体积?
(2)已知底面直径d和高h,怎样求圆柱的体积?
(3)已知底面周长C和高h,怎样求圆柱的体积?
尝试解决下面的问题,并与同伴交流。
笑笑了解到一根柱子的底面半径为0.4m,高为5m。你能算出它的体积吗?
V = πr2h
V = πr2h
=3.14×0.42×5
=3.14×0.16×5
=3.14×0.8
=2.512(m3)
答:需要2.512m3木材。
1. 我会判断 。
(1)长方形沿长旋转可以得到圆柱。( )
巩固练习
(2)等底等高的圆柱和长方体的体积相等。( )
√
√
2.我会选择 。
(1)把圆柱按右图方法切割后拼成近似的长方体,底面积( ),体积( )。
A.变大了 B.变小了 C.不变
C
C
3.计算下面各圆柱的体积。
60×4
=240(cm3)
3.14×12×5
=3.14×1×5
=15.7(cm3)
V = Sh
V = πr2h
我会计算
尝试解决下面的问题,并与同伴交流。
从水杯里面量,水杯的底面直径是6 cm,高是16 cm,这个水杯能装多少毫升水?
V = π(d÷2)2h
3.14×(6÷2)2×16
=3.14×9×16
=452.16(cm3)
=452.16(毫升)
答:一个杯子能装452.16毫升水。
水杯能装水的体积就是水杯的容积。
我们把圆柱转化成长方体
这节课你们都学会了哪些知识?
课堂小结
圆柱的体积
底面积
高
=
×
V = Sh
V = πr2h
V =π(d÷2)2h
V =π(C÷π÷2)2h
圆柱体转化成长方体,体积没有变,那么表面积有没有变化呢?如果变了,是增加了,还是减少了?
课后思考
穷则变,变则通,通则久。
——《周易·系辞下》
指事物发展到了极点,就要发生变化,才会使事物的发展不受阻塞,事物才能不断地发展。道行不通时选择变化,变化了后就会豁然开朗,行得通则可以长久。
圆柱的体积(1)
北师大版·六年级下册
要知道需要柱子需要多少木材,就需要计算柱子的体积,而柱子是圆柱形,怎样计算圆柱的体积呢?
探究新知
什么是圆柱的
体积呢?
圆柱所占空间的大小是圆柱的体积。
a
b
h
a
a
a
回想一下,我们学过哪些立体图形的体积?
V长方体= abh
V正方体=a3
长方体(或正方体)的体积=底面积×高
V = S × h
V = Sh
S
S
a
b
h
a
a
a
S
S
V = Sh
V = Sh
想一想,怎样计算圆柱的体积呢?
S
h
猜想:圆柱体积的方法是否和长方体、正方体相同?
圆柱的体积=底面积×高
尝试验证你的猜想,并与同伴交流。
通过叠硬币,我们发现硬币的
( )是固定的,每增加一枚硬币,( )就增加一些,( )也随之增大。
方法一:堆硬币法
由此可见:
底面积
高
体积
想办法验证猜想是否正确?
想办法验证猜想是否正确?
方法二:转化法
想办法验证猜想是否正确?
方法二:转化法
切开后拼成的物体会有什么变化?什么没变?
如果用V表示圆柱的体积,S表示圆柱的底面积,
h表示圆柱的高,那么圆柱的体积计算公式可以表示为
圆柱的体积
底面积
高
=
×
V = Sh
S
h
思考还能怎样计算圆柱的体积?
圆柱底面积
长方体底面积
长方体的高
圆柱的高
底面圆周长的一半
底面圆的半径
迁移:圆柱转化成近似长方体
V = πr2h
想办法验证猜想是否正确?
方法二:转化法
完成导学单:
V =π(d÷2)2h
V = πr2h
V =π(C÷π÷2)2h
(1)已知底面半径r和高h,怎样求圆柱的体积?
(2)已知底面直径d和高h,怎样求圆柱的体积?
(3)已知底面周长C和高h,怎样求圆柱的体积?
尝试解决下面的问题,并与同伴交流。
笑笑了解到一根柱子的底面半径为0.4m,高为5m。你能算出它的体积吗?
V = πr2h
V = πr2h
=3.14×0.42×5
=3.14×0.16×5
=3.14×0.8
=2.512(m3)
答:需要2.512m3木材。
1. 我会判断 。
(1)长方形沿长旋转可以得到圆柱。( )
巩固练习
(2)等底等高的圆柱和长方体的体积相等。( )
√
√
2.我会选择 。
(1)把圆柱按右图方法切割后拼成近似的长方体,底面积( ),体积( )。
A.变大了 B.变小了 C.不变
C
C
3.计算下面各圆柱的体积。
60×4
=240(cm3)
3.14×12×5
=3.14×1×5
=15.7(cm3)
V = Sh
V = πr2h
我会计算
尝试解决下面的问题,并与同伴交流。
从水杯里面量,水杯的底面直径是6 cm,高是16 cm,这个水杯能装多少毫升水?
V = π(d÷2)2h
3.14×(6÷2)2×16
=3.14×9×16
=452.16(cm3)
=452.16(毫升)
答:一个杯子能装452.16毫升水。
水杯能装水的体积就是水杯的容积。
我们把圆柱转化成长方体
这节课你们都学会了哪些知识?
课堂小结
圆柱的体积
底面积
高
=
×
V = Sh
V = πr2h
V =π(d÷2)2h
V =π(C÷π÷2)2h
圆柱体转化成长方体,体积没有变,那么表面积有没有变化呢?如果变了,是增加了,还是减少了?
课后思考
穷则变,变则通,通则久。
——《周易·系辞下》
指事物发展到了极点,就要发生变化,才会使事物的发展不受阻塞,事物才能不断地发展。道行不通时选择变化,变化了后就会豁然开朗,行得通则可以长久。
