2023-2024学年北师大版八年级数学上册4.1函数 课件(共33张PPT)
文档属性
| 名称 | 2023-2024学年北师大版八年级数学上册4.1函数 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 18.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览










文档简介
(共33张PPT)
4.1 函 数
北师大版·数学 八年级上册
回
顾
丰富的
现实情境
自变量和因变量
变量之间关系的探索和表示
利用变量之间的关系解决问题、进行预测
列表法
关系式
图像法
变量之间的关系
函数是刻画变量之间关系的常用模型.
学习目标
03
通过三个具体实例的探索,初步理解函数的概念,能判断两个变量间的关系是否为函数关系并能举出实例;
01
通过具体实例的对比,了解函数的三种表示方法;能确定简单问题中的函数自变量的取值范围并会求出函数值;
02
经历从具体实例中抽象出函数概念的过程,进一步感悟抽象的数学思想,积累抽象概括的活动经验;初步形成利用函数的观点认识现实世界的意识,体会函数的模型思想.
02
情境导学
情境导学
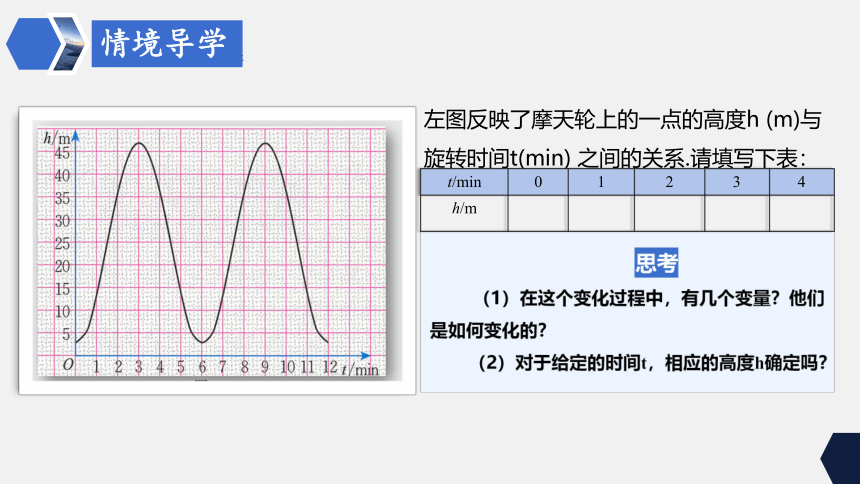
左图反映了摩天轮上的一点的高度h (m)与旋转时间t(min) 之间的关系.请填写下表:
思考
(1)在这个变化过程中,有几个变量?他们是如何变化的?
(2)对于给定的时间t,相应的高度h确定吗?
t/min 0 1 2 3 4
h/m
情境导学
思考
(1)在这个变化过程中,有几个变量?他们是如何变化的?
(2)给定层数,你能求出相应的物体总数吗?
情境导学
思考
(1)在这个变化过程中,有几个变量?
(2)当t分别为-43、-27、0、18时,相应的紧热力学温度T是多少?
(3)给定一个大于-273℃的t值,你都能求出相应的T值吗?
数学的概念应该怎么获得?
“可以从大量同类事物的不同例证中找到它们的共同的关键特征。”
——选自《数学概念的获得》
合作研学
问题1:以小组为单位,交流分析以上3个变化过程中,一个量随另一个量的变化而变化的现象,并在学案上记录变化过程中的相同点,讨论结束后请小组代表发言;
情境导学
合作研学
合作一
问题情境 分析 摩天轮问题
罐头盒问题
温度问题
层数n 1 2 3 4 5 …
物体总数y …
6
10
15
1
3
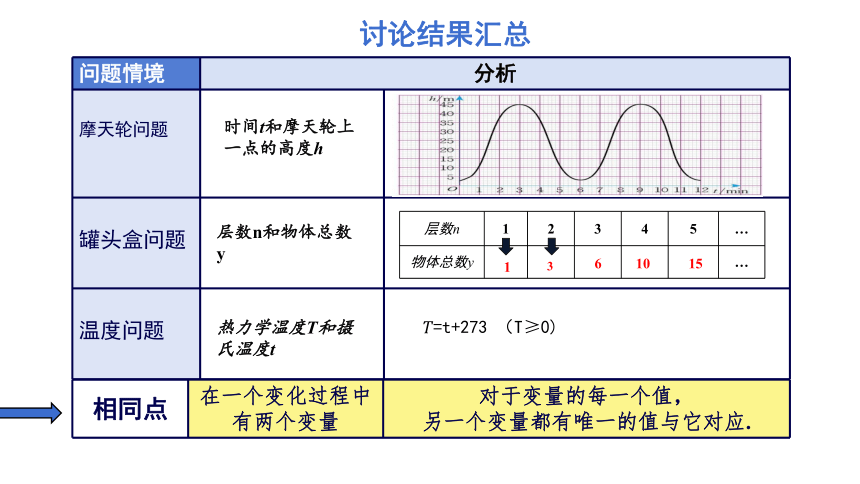
时间t和摩天轮上一点的高度h
层数n和物体总数y
热力学温度T和摄氏温度t
讨论结果汇总
相同点 在一个变化过程中 有两个变量 对于变量的每一个值,
另一个变量都有唯一的值与它对应.
=t+273 (T≥0)
情境导学
合作研学
问题2:请你用自己的语言给函数下一个定义;
合作一
情境导学
合作研学
函数的概念
一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数. 其中x是自变量,y是因变量.
问题情境 分析 摩天轮问题
罐头盒问题
温度问题
层数n 1 2 3 4 5 …
物体总数y …
6
10
15
1
3
时间t和摩天轮上一点的高度h
层数n和物体总数y
热力学温度T和摄氏温度t
讨论结果汇总
相同点 在一个变化过程中 有两个变量 对于变量的每一个值,
另一个变量都有唯一的值与它对应.
=t+273 (T≥0)
h 是 t 的函数
y是 n 的函数
T是t的函数
问题3:这3个函数的表示有什么不同呢?
问题4:这三个函数中,自变量能取哪些值?
情境导学
合作研学
合作一
问题情境 自变量取值范围 因变量 对应关系
摩天轮问题
弹簧问题
刹车问题
x/kg 0 1 2 3 4 …
y/cm …
4
4.5
5
3
3.5
所挂物体质量x
巴士行驶速度v
弹簧长度y
刹车后滑行距离s
时间t
摩天轮上
一点的高度h
=
图象法
列表法
关系式法
t≥0
x≥0
0≤v≤100
表示方法
函数的 概念 一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
问题情境 自变量取值范围 函数值 对应关系
摩天轮问题
罐头盒问题
温度问题 摄氏温度t =t+273 (T≥0)
层数n
时间t
当t=1时,h=14;
当t=2时,h=36;
图象法
列表法
关系式法
t≥0
n≥0
表示方法
函数的 概念 一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
当n=1时,y=1;
当n=4时,y=10;
当t=0时,T=273
当t=18时,T=291
层数n 1 2 3 4 5 …
物体总数y 1 3 6 10 15 …
t≥-273℃
问题情境 自变量取值范围 函数值 对应关系
摩天轮问题
弹簧问题
刹车问题
x/kg 0 1 2 3 4 …
y/cm …
4
4.5
5
3
3.5
所挂物体质量x
巴士行驶速度v
时间t
=
图象法
列表法
关系式法
t≥0
x≥0
0≤v≤100
表示方法
对于自变量在可取值范围内的一个确定的值a,函数有唯一确定的对应值,这个对应值称为
当自变量等于a时的函数值.
函数的 概念 一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
在中国,古人将“函”字与“含”字通用,都有着“包含”的意思,还用“天、地、人、物”四个字来表示四个不同的未知数或变量.
“函数”的由来
数学家、天文学家、翻译家和教育家,近代科学的先驱者李善兰给出的定义是:“凡式中含天,为天之函数.”
“概念是思维的细胞,我们不仅需要理解概念的内涵,还需要明确概念的外延.”
——《中学数学教学概论》
编:观察生活,寻找一个变化过程,说明其中的函数关系,并指出自变量的取值范围;
(组内成员互相判断对方的是否能构成函数关系,5分钟后请以小组为单位展示你们的精彩成果.)
情境导学
合作研学
合作二
辨:下列问题中,一个变量是否是另一个变量的函数?
如果是,请指出自变量.
情境导学
合作研学
合作二
(1)改变正方形的边长 x,正方形的面积 S 随之变化;
(2)点P是数轴上的一个动点,它到原点的距离记为 x, 它对应的实数为 y,
y 随 x 的变化而变化.
辨:(3)如图① ②,x是自变量,则y是x的函数吗?为什么
情境导学
合作研学
合作二
x
y
o
2
-2
x
y
o
-1
1
-2
图①
图②
情境导学
合作研学
在线检学
反思悟学
数学知识
数学方法
数学思想
函数
本质属性
数学抽象
自变量取值范围
函数值
概念
表示
利用函数的观点
认识世界、解决问题
数学建模
内涵
外延
变量间的关系
知识
方法
丰富的现实情境
思想
初中数学
初中数学
4.1 函 数
北师大版·数学 八年级上册
回
顾
丰富的
现实情境
自变量和因变量
变量之间关系的探索和表示
利用变量之间的关系解决问题、进行预测
列表法
关系式
图像法
变量之间的关系
函数是刻画变量之间关系的常用模型.
学习目标
03
通过三个具体实例的探索,初步理解函数的概念,能判断两个变量间的关系是否为函数关系并能举出实例;
01
通过具体实例的对比,了解函数的三种表示方法;能确定简单问题中的函数自变量的取值范围并会求出函数值;
02
经历从具体实例中抽象出函数概念的过程,进一步感悟抽象的数学思想,积累抽象概括的活动经验;初步形成利用函数的观点认识现实世界的意识,体会函数的模型思想.
02
情境导学
情境导学
左图反映了摩天轮上的一点的高度h (m)与旋转时间t(min) 之间的关系.请填写下表:
思考
(1)在这个变化过程中,有几个变量?他们是如何变化的?
(2)对于给定的时间t,相应的高度h确定吗?
t/min 0 1 2 3 4
h/m
情境导学
思考
(1)在这个变化过程中,有几个变量?他们是如何变化的?
(2)给定层数,你能求出相应的物体总数吗?
情境导学
思考
(1)在这个变化过程中,有几个变量?
(2)当t分别为-43、-27、0、18时,相应的紧热力学温度T是多少?
(3)给定一个大于-273℃的t值,你都能求出相应的T值吗?
数学的概念应该怎么获得?
“可以从大量同类事物的不同例证中找到它们的共同的关键特征。”
——选自《数学概念的获得》
合作研学
问题1:以小组为单位,交流分析以上3个变化过程中,一个量随另一个量的变化而变化的现象,并在学案上记录变化过程中的相同点,讨论结束后请小组代表发言;
情境导学
合作研学
合作一
问题情境 分析 摩天轮问题
罐头盒问题
温度问题
层数n 1 2 3 4 5 …
物体总数y …
6
10
15
1
3
时间t和摩天轮上一点的高度h
层数n和物体总数y
热力学温度T和摄氏温度t
讨论结果汇总
相同点 在一个变化过程中 有两个变量 对于变量的每一个值,
另一个变量都有唯一的值与它对应.
=t+273 (T≥0)
情境导学
合作研学
问题2:请你用自己的语言给函数下一个定义;
合作一
情境导学
合作研学
函数的概念
一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数. 其中x是自变量,y是因变量.
问题情境 分析 摩天轮问题
罐头盒问题
温度问题
层数n 1 2 3 4 5 …
物体总数y …
6
10
15
1
3
时间t和摩天轮上一点的高度h
层数n和物体总数y
热力学温度T和摄氏温度t
讨论结果汇总
相同点 在一个变化过程中 有两个变量 对于变量的每一个值,
另一个变量都有唯一的值与它对应.
=t+273 (T≥0)
h 是 t 的函数
y是 n 的函数
T是t的函数
问题3:这3个函数的表示有什么不同呢?
问题4:这三个函数中,自变量能取哪些值?
情境导学
合作研学
合作一
问题情境 自变量取值范围 因变量 对应关系
摩天轮问题
弹簧问题
刹车问题
x/kg 0 1 2 3 4 …
y/cm …
4
4.5
5
3
3.5
所挂物体质量x
巴士行驶速度v
弹簧长度y
刹车后滑行距离s
时间t
摩天轮上
一点的高度h
=
图象法
列表法
关系式法
t≥0
x≥0
0≤v≤100
表示方法
函数的 概念 一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
问题情境 自变量取值范围 函数值 对应关系
摩天轮问题
罐头盒问题
温度问题 摄氏温度t =t+273 (T≥0)
层数n
时间t
当t=1时,h=14;
当t=2时,h=36;
图象法
列表法
关系式法
t≥0
n≥0
表示方法
函数的 概念 一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
当n=1时,y=1;
当n=4时,y=10;
当t=0时,T=273
当t=18时,T=291
层数n 1 2 3 4 5 …
物体总数y 1 3 6 10 15 …
t≥-273℃
问题情境 自变量取值范围 函数值 对应关系
摩天轮问题
弹簧问题
刹车问题
x/kg 0 1 2 3 4 …
y/cm …
4
4.5
5
3
3.5
所挂物体质量x
巴士行驶速度v
时间t
=
图象法
列表法
关系式法
t≥0
x≥0
0≤v≤100
表示方法
对于自变量在可取值范围内的一个确定的值a,函数有唯一确定的对应值,这个对应值称为
当自变量等于a时的函数值.
函数的 概念 一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量,y是因变量.
在中国,古人将“函”字与“含”字通用,都有着“包含”的意思,还用“天、地、人、物”四个字来表示四个不同的未知数或变量.
“函数”的由来
数学家、天文学家、翻译家和教育家,近代科学的先驱者李善兰给出的定义是:“凡式中含天,为天之函数.”
“概念是思维的细胞,我们不仅需要理解概念的内涵,还需要明确概念的外延.”
——《中学数学教学概论》
编:观察生活,寻找一个变化过程,说明其中的函数关系,并指出自变量的取值范围;
(组内成员互相判断对方的是否能构成函数关系,5分钟后请以小组为单位展示你们的精彩成果.)
情境导学
合作研学
合作二
辨:下列问题中,一个变量是否是另一个变量的函数?
如果是,请指出自变量.
情境导学
合作研学
合作二
(1)改变正方形的边长 x,正方形的面积 S 随之变化;
(2)点P是数轴上的一个动点,它到原点的距离记为 x, 它对应的实数为 y,
y 随 x 的变化而变化.
辨:(3)如图① ②,x是自变量,则y是x的函数吗?为什么
情境导学
合作研学
合作二
x
y
o
2
-2
x
y
o
-1
1
-2
图①
图②
情境导学
合作研学
在线检学
反思悟学
数学知识
数学方法
数学思想
函数
本质属性
数学抽象
自变量取值范围
函数值
概念
表示
利用函数的观点
认识世界、解决问题
数学建模
内涵
外延
变量间的关系
知识
方法
丰富的现实情境
思想
初中数学
初中数学
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
