9.1.1简单随机抽样 第2课时 课件(共18张PPT)
文档属性
| 名称 | 9.1.1简单随机抽样 第2课时 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 21:33:36 | ||
图片预览






文档简介
(共18张PPT)
9.1.1 简单随机抽样
第2课时
一般地,设一个总体含有N个个体,从中逐个地抽取n个个体作为样本(n≤N),如果每次抽取时总体内的各个个体被抽到的机会都相等,这种抽样方法叫做简单随机抽样。
温故知新
①有限性;
1.简单随机抽样的概念
2.简单随机抽样的常用方法:
简单随机抽样的特点:
②逐一性;
③等可能性.
(1)抽签法:
②制签
①编号
③拌匀
④抽签
⑤取样
(2)抽签法:
①编号
③取样
②选号
探究新知
平均数(均值)
中位数
最大值 最小值
极差
......
问题1:回忆初中知识,说说一组数据当中会有怎样的数据特征呢?
探究新知
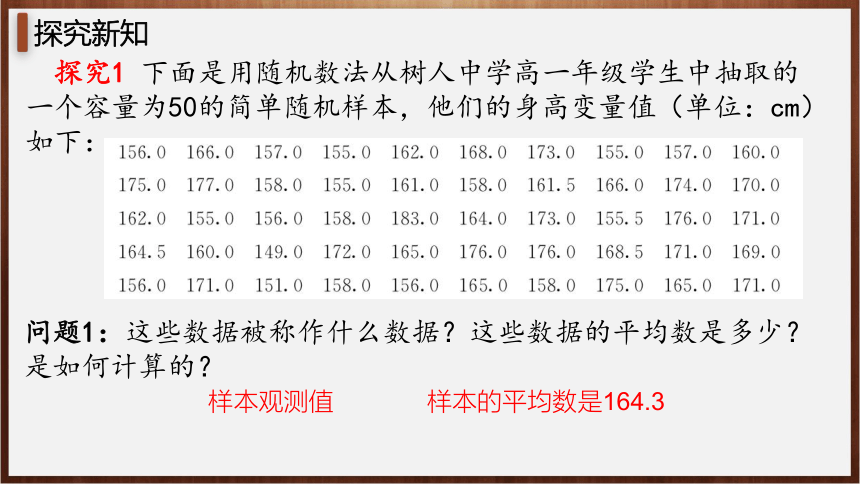
探究1 下面是用随机数法从树人中学高一年级学生中抽取的一个容量为50的简单随机样本,他们的身高变量值(单位:cm)如下:
样本观测值
问题1:这些数据被称作什么数据?这些数据的平均数是多少?
是如何计算的?
样本的平均数是164.3
探究新知
问题2:由这些样本观测数据,我们可以计算出样本的平均数为164.3。那么可以估计树人中学高一年级学生的平均身高一定是164.3cm吗?
不能
据此可估计树人中学高一年级的平均身高为164.3cm左右
样本数据 估计 总体数据
我们通过简单随机抽样得到部分学生的平均身高,并把样本平均身高作为树人中学高一年级所有学生平均身高的估计值
探究新知
一般地,总体中有N个个体,它们的变量值分别为,则称
1.总体均值(总体平均数):
为总体均值,又称总体平均数.
2.样本均值(样本平均数):
如果从总体中抽取一个容量为n的样本,它们的变量值分别为,则称
为样本均值,又称样本平均数.
在简单随机抽样中常用样品平均数估计总体平均数.
探究新知
3.加权平均数:
如果总体的个变量值中,不同的值共有个,不妨记为其中出现的频数则总体均值还可以写成加权平均数的形式
探究新知
问题3:另取50个样本,这50个样本的样本平均数还是164.3cm吗?
不一定是
问题4:取100个样本,这100个样本的平均数会发怎样的改变呢?
可能更靠近总体的平均数.
探究新知
探究2 小明想考察一下简单随机抽样的估计效果.他从树人中学医务室得到了高一年级学生身高的所有数据,算出整个年级学生的平均身高为165.0 cm.
然后小明用简单随机抽样的方法,从这些数据中抽取了样本量为50和100的样本各10个,分别计算出样本平均数,如表所示.从小明多次抽样所得的结果中,你有什么发现
探究新知
为了更方便地观察数据,可把这20次试验的平均数用散点图表示出来。
图中的红线表示树人中学高一年级全体学生身高的平均数。
问题5 从图表中,你发现了哪些数据特征?
探究新知
样本平均数是随机性的,总体平均数是确定的
(1)样本平均数有怎样的特征
(3)比较样本量为50和样本量为100的样本平均数波动幅度的大小
(2)样本半均数与总体半均数有怎样的联系
大部分样本平均数离总体平均数不远,在总体平均数附近波动。
增加样本量可以提高估计效果
探究新知
探究3 眼睛是心灵的窗口,保护好视力非常重要.树人中学在“全国爱眼日”前,想通过简单随机抽样的方法,了解一下全校2174名学生中视力不低于5.0的学生所占的比例,你觉得该怎么做?同桌之间进行讨论,说说你的办法!
方法一:将所有同学的视力情况全部调查清楚,接着再统计视力不低于50的同学,最后计算。(全面调查)
方法二:在所有同学中抽取一部分的同学进行视力调查,可以抽取一个容量为50的简单随机样本,在样本中统计视力不低于50的同学。由样本均值估计总体均值。(抽样调查)
探究新知
方法三:为了便于问题的描述,记“视力低于5.0”的为0,记“视力不低于5.0”的为1,则第i个(i=1,2,...,2174)学生的视力变量值记为Yi,变量Yi的表达式为
那么在全校学生中,“视力不低于5.0”的人数用变量Yi表示为
在总体中,“视力不低于5.0”的人数所占的比例P为多少?
探究新知
类似地,若抽取容量为n的样本,把它们的视力变量值分别记为y1,y2,…,yn,则在样本中,“视力不低于5.0”的人数所占的比例p就是学生视力变量的样本平均数:
现在,我们从树人中学所有学生中抽取一个容量为50的简单随机样本,其视力变量取值如下:
由样本观测数据,我们可以计算出样本平均数为
=0.54
因此可以估计全体学生中“视力不低于5.0”的比例约为0.54.
当堂练习
(A) 一定为5.5kW·h
(B) 高于为5.5kW·h
(C) 低于为5.5kW·h
(D) 约为5.5kW·h
1.为了合理调配电力资源,某市欲了解全市50 000户居民的日用电量。若通过简单随机抽样从中抽取了300户进行调查,得到其日用电量的平均数为5.5 kW·h,则可以推测全市居民用户日用电量的平均数( )
D
当堂练习
2.在学生身高的调查中,小明和小华分别独立进行了简单随机抽样调查.小明调查的样本平均数为166.4,样本量为100;小华调查的样本平均数为164.7,样本量为200.你更愿意把哪个值作为总体平均数的估计?是不是你选的值一定比另一个更接近总体平均数?说说你的理由.
更愿意把164.7作为总体平均数的估计,因为增加样本容量可以提高估计效果。
但所选的值不一定比另一个更接近总体平均数,因为样本的平均数具有随机性。
课堂小结
一般地,总体中有N个个体,它们的变量值分别为,则称
1.总体均值(总体平均数):
为总体均值,又称总体平均数.
2.样本均值(样本平均数):
如果从总体中抽取一个容量为n的样本,它们的变量值分别为,则称
为样本均值,又称样本平均数.
3.思想:用样品平均数估计总体平均数.
课后作业
课本习题9.1中综合运用的第6题
9.1.1 简单随机抽样
第2课时
一般地,设一个总体含有N个个体,从中逐个地抽取n个个体作为样本(n≤N),如果每次抽取时总体内的各个个体被抽到的机会都相等,这种抽样方法叫做简单随机抽样。
温故知新
①有限性;
1.简单随机抽样的概念
2.简单随机抽样的常用方法:
简单随机抽样的特点:
②逐一性;
③等可能性.
(1)抽签法:
②制签
①编号
③拌匀
④抽签
⑤取样
(2)抽签法:
①编号
③取样
②选号
探究新知
平均数(均值)
中位数
最大值 最小值
极差
......
问题1:回忆初中知识,说说一组数据当中会有怎样的数据特征呢?
探究新知
探究1 下面是用随机数法从树人中学高一年级学生中抽取的一个容量为50的简单随机样本,他们的身高变量值(单位:cm)如下:
样本观测值
问题1:这些数据被称作什么数据?这些数据的平均数是多少?
是如何计算的?
样本的平均数是164.3
探究新知
问题2:由这些样本观测数据,我们可以计算出样本的平均数为164.3。那么可以估计树人中学高一年级学生的平均身高一定是164.3cm吗?
不能
据此可估计树人中学高一年级的平均身高为164.3cm左右
样本数据 估计 总体数据
我们通过简单随机抽样得到部分学生的平均身高,并把样本平均身高作为树人中学高一年级所有学生平均身高的估计值
探究新知
一般地,总体中有N个个体,它们的变量值分别为,则称
1.总体均值(总体平均数):
为总体均值,又称总体平均数.
2.样本均值(样本平均数):
如果从总体中抽取一个容量为n的样本,它们的变量值分别为,则称
为样本均值,又称样本平均数.
在简单随机抽样中常用样品平均数估计总体平均数.
探究新知
3.加权平均数:
如果总体的个变量值中,不同的值共有个,不妨记为其中出现的频数则总体均值还可以写成加权平均数的形式
探究新知
问题3:另取50个样本,这50个样本的样本平均数还是164.3cm吗?
不一定是
问题4:取100个样本,这100个样本的平均数会发怎样的改变呢?
可能更靠近总体的平均数.
探究新知
探究2 小明想考察一下简单随机抽样的估计效果.他从树人中学医务室得到了高一年级学生身高的所有数据,算出整个年级学生的平均身高为165.0 cm.
然后小明用简单随机抽样的方法,从这些数据中抽取了样本量为50和100的样本各10个,分别计算出样本平均数,如表所示.从小明多次抽样所得的结果中,你有什么发现
探究新知
为了更方便地观察数据,可把这20次试验的平均数用散点图表示出来。
图中的红线表示树人中学高一年级全体学生身高的平均数。
问题5 从图表中,你发现了哪些数据特征?
探究新知
样本平均数是随机性的,总体平均数是确定的
(1)样本平均数有怎样的特征
(3)比较样本量为50和样本量为100的样本平均数波动幅度的大小
(2)样本半均数与总体半均数有怎样的联系
大部分样本平均数离总体平均数不远,在总体平均数附近波动。
增加样本量可以提高估计效果
探究新知
探究3 眼睛是心灵的窗口,保护好视力非常重要.树人中学在“全国爱眼日”前,想通过简单随机抽样的方法,了解一下全校2174名学生中视力不低于5.0的学生所占的比例,你觉得该怎么做?同桌之间进行讨论,说说你的办法!
方法一:将所有同学的视力情况全部调查清楚,接着再统计视力不低于50的同学,最后计算。(全面调查)
方法二:在所有同学中抽取一部分的同学进行视力调查,可以抽取一个容量为50的简单随机样本,在样本中统计视力不低于50的同学。由样本均值估计总体均值。(抽样调查)
探究新知
方法三:为了便于问题的描述,记“视力低于5.0”的为0,记“视力不低于5.0”的为1,则第i个(i=1,2,...,2174)学生的视力变量值记为Yi,变量Yi的表达式为
那么在全校学生中,“视力不低于5.0”的人数用变量Yi表示为
在总体中,“视力不低于5.0”的人数所占的比例P为多少?
探究新知
类似地,若抽取容量为n的样本,把它们的视力变量值分别记为y1,y2,…,yn,则在样本中,“视力不低于5.0”的人数所占的比例p就是学生视力变量的样本平均数:
现在,我们从树人中学所有学生中抽取一个容量为50的简单随机样本,其视力变量取值如下:
由样本观测数据,我们可以计算出样本平均数为
=0.54
因此可以估计全体学生中“视力不低于5.0”的比例约为0.54.
当堂练习
(A) 一定为5.5kW·h
(B) 高于为5.5kW·h
(C) 低于为5.5kW·h
(D) 约为5.5kW·h
1.为了合理调配电力资源,某市欲了解全市50 000户居民的日用电量。若通过简单随机抽样从中抽取了300户进行调查,得到其日用电量的平均数为5.5 kW·h,则可以推测全市居民用户日用电量的平均数( )
D
当堂练习
2.在学生身高的调查中,小明和小华分别独立进行了简单随机抽样调查.小明调查的样本平均数为166.4,样本量为100;小华调查的样本平均数为164.7,样本量为200.你更愿意把哪个值作为总体平均数的估计?是不是你选的值一定比另一个更接近总体平均数?说说你的理由.
更愿意把164.7作为总体平均数的估计,因为增加样本容量可以提高估计效果。
但所选的值不一定比另一个更接近总体平均数,因为样本的平均数具有随机性。
课堂小结
一般地,总体中有N个个体,它们的变量值分别为,则称
1.总体均值(总体平均数):
为总体均值,又称总体平均数.
2.样本均值(样本平均数):
如果从总体中抽取一个容量为n的样本,它们的变量值分别为,则称
为样本均值,又称样本平均数.
3.思想:用样品平均数估计总体平均数.
课后作业
课本习题9.1中综合运用的第6题
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
