4.1函数随堂练习-北师大版数学八年级上册(含答案)
文档属性
| 名称 | 4.1函数随堂练习-北师大版数学八年级上册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 546.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览




文档简介
4.1函数随堂练习-北师大版数学八年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
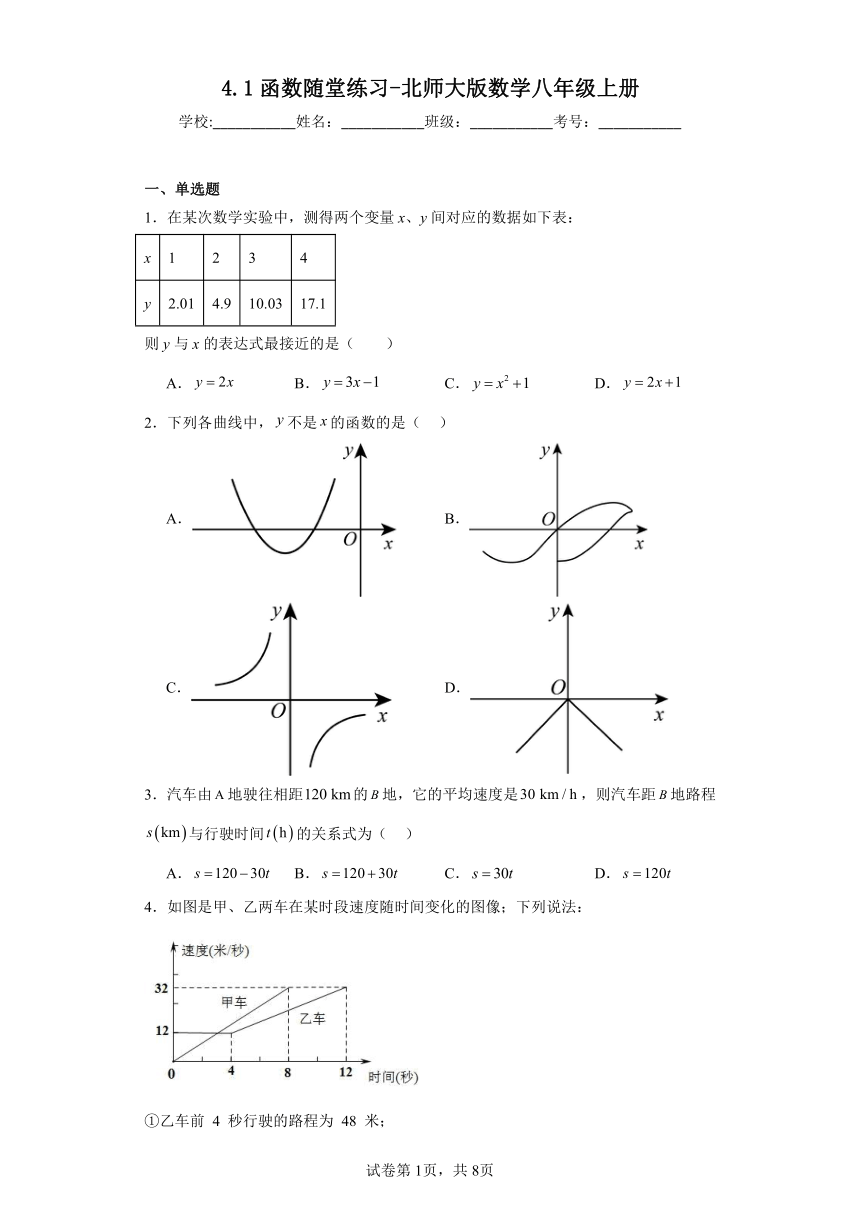
1.在某次数学实验中,测得两个变量x、y间对应的数据如下表:
x 1 2 3 4
y 2.01 4.9 10.03 17.1
则y与x的表达式最接近的是( )
A. B. C. D.
2.下列各曲线中,不是的函数的是( )
A. B.
C. D.
3.汽车由地驶往相距的地,它的平均速度是,则汽车距地路程与行驶时间的关系式为( )
A. B. C. D.
4.如图是甲、乙两车在某时段速度随时间变化的图像;下列说法:
①乙车前 4 秒行驶的路程为 48 米;
②在 0 到 8 秒内甲车的速度每秒增加 4 米;
③两车到第 3 秒时行驶的路程相等;
④在 4 到 8 秒内甲车的速度都大于乙车的速度.
其中正确的有( )
A.1 个 B.2 个 C.3 个 D.4 个
5.如图是加油机上的数据显示牌,其中的变量是( )
A.金额 B.单价 C.油量 D.金额和油量
6.一个直角三角形的两条直角边长的和为20cm,其中一直角边长为xcm,面积为ycm2,则y与x的函数的关系式是( )
A.y=10x﹣x2 B.y=10x C.y=﹣x D.y=x(10﹣x)
7.周末小兰外出爬山,她从山脚爬到山顶的过程中,途中休息了一段时间,设她从山脚出发后所用时间为(分钟),所走路程为(米),与之间的函数关系如图所示,下列说法错误的是( )
A.小兰途中休息了15分钟
B.小兰爬上山顶所走路程为8200米
C.小兰从山脚爬到山顶共用了100分钟
D.小兰休息前的速度大于休息后的速度
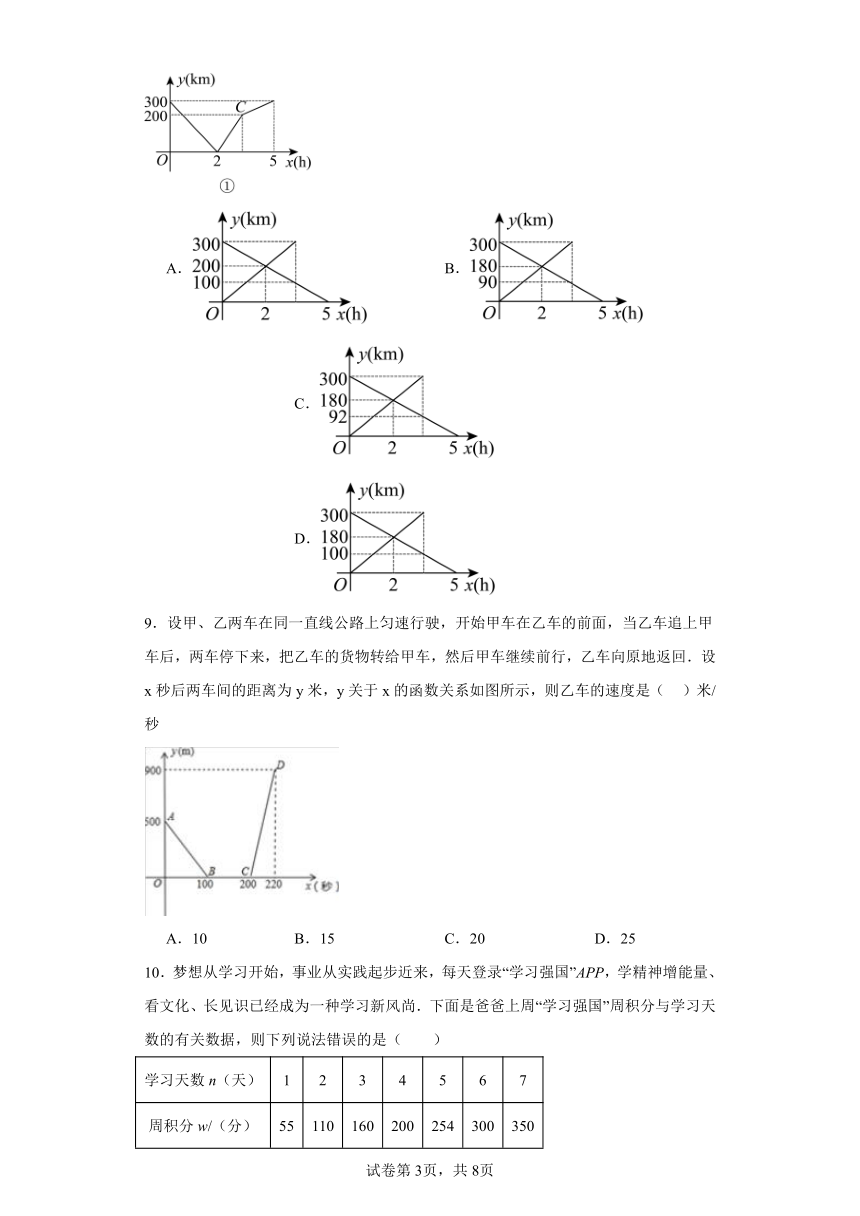
8.甲、乙两辆汽车同时分别从相距300千米的A、B两座城市出发相向而行.行驶过程中两车速度不变,甲车到达B城,立即停止,乙车继续行驶,到达A城后停止.若以两车之间的距离为y轴,以两车行驶时间为x轴,画出如图①所示函数图象.若以两车到A城的距离为y轴,以两车行驶时间为x轴在同一坐标体系看画出图象,与图①函数图象意义一致的是( )
A. B. C. D.
9.设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y米,y关于x的函数关系如图所示,则乙车的速度是( )米/秒
A.10 B.15 C.20 D.25
10.梦想从学习开始,事业从实践起步近来,每天登录“学习强国”APP,学精神增能量、看文化、长见识已经成为一种学习新风尚.下面是爸爸上周“学习强国”周积分与学习天数的有关数据,则下列说法错误的是( )
学习天数n(天) 1 2 3 4 5 6 7
周积分w/(分) 55 110 160 200 254 300 350
A.在这个变化过程中,学习天数是自变量,周积分是因变量
B.周积分随学习天数的增加而增加
C.周积分w与学习天数n的关系式为w=50n
D.天数每增加1天,周积分的增长量不一定相同
二、填空题
11.等腰三角形的顶角y与底角x之间是函数关系吗? (是或不是中选择)
12.描点法画函数图象的一般步骤:
第一步: .在自变量取值范围内选定一些值.通过函数关系式求出对应函数值列成表格.
第二步: .在直角坐标系中,以自变量的值为横坐标,相应函数值为纵坐标,描出表中对应各点.
第三步: .按照坐标由小到大的顺序把所有点用平滑曲线连结起来.
13.在函数中,自变量的取值范围是 .
14. (2018年河南省开封市中考模拟考试(4月)) 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角三角形ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,则y与x的解析式是 .
15.函数中,自变量的取值范围为 .
16.由于惯性的作用,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”.
某公司设计了一款新型汽车,需要对它的刹车性能进行测试.设汽车的刹车距离为单位:,车速为单位:,根据测得的数据,与的函数关系如图所示.
(1)若该款汽车某次测试的刹车距离为 ,估计该车的速度约为 ;
(2)在测试中发现该款汽车在车速达到某一数值时,其刹车距离的数值恰好是车速数值的,则此时的车速约为 结果取整数).
17.从A市到B市汽车行驶的高速公路里程固定.假设汽车匀速行驶,汽车行驶的速度v(千米)时)与速度t(小时)的函数图象如图所示.若高速公路的速度限定不超过每小时120千米,则汽车从A市到B市行驶的最短时间为 小时.
18.函数可用表示,例如,当时,,若函数,则的值为 .
19.一个长为120m,宽为100m的矩形场地,要扩建为一个正方形场地,设长增加xm,宽增加ym,则y与x之间的函数关系式为 .
20.对于函数.当x=2时,y= .
三、解答题
21.小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的书店,买到书后继续去学校.如图是他本次上学所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程为________米;
(2)在整个上学途中________时间段小明骑车速度最快,最快的速度是_______米/分;
(3)小明在书店停留了________分钟;
(4)本次上学途中,小明一共行驶了多少米?
22.函数图象是研究函数的重要工具.结合已有的学习函数图象和性质的经验,请画出函数的图象并探究该函数的性质.
(1)绘制函数图象
①列表:下表是中x与y的几组对应值,其中a=______;
x … -4 -3 -2 -1 -0.5 0 0.5 1 2 3 4 …
y … -1 -2 a -2 -1 …
②描点:根据表中的数值描点(x,y),请补充描出点(0,a);
③连线:用平滑的曲线顺次连接各点,请画出函数图象.
(2)探究函数性质:请写出函数的两条性质:①______;②______;
(3)运用函数图象及性质:根据函数图象,写出不等式的解集是______.
23.小李骑自行车从家出发到距离家2000米远的水上公园,如图所示是小李从家到公园路途中离家的距离与离家时间之间关系的图象.
(1)在这个变化过程中,自变量、因变量分别是什么?
(2)观察图象分析,出发后10分钟到15分钟之间可能发生了什么情况?
(3)求这一段骑行中的最高速度是多少?
(4)用自己的语言大致描述小李骑行的情况.
24.小明骑车野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(千米)与小明离家时间x(小时)的函数图象,已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度;
(2)小明在甲地游玩多少时间?
(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.
25.如图,在中,,为边上一动点,,垂足为N.设A,M两点间的距离为xcm(),B,N两点间的距离为ycm(当M点和B点重合时,B,N两点间的距离为0).
小明根据学习函数的经验,对因变量y随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整.
(1)列表:下表的已知数据是根据A,M两点间的距离x进行取点、画图、测量,分别得到的y与x的几组对应值:
x/cm 0 0.5 1 1.5 1.8 2 2.5 3 3.5 4 4.5 5
y/cm 4 3.96 3.79 3.47 a 2.99 2.40 1.79 1.23 0.74 0.33 0
请你通过计算,补全表格: ;
(2)描点、连线:在平面直角坐标系中,描出表中各组数值所对应的点(x,y),并画出y关于x的函数图象;
(3)探究性质:随着自变量x的不断增大,函数y的变化趋势: .
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.B
3.A
4.C
5.D
6.A
7.B
8.D
9.D
10.C
11.是
12. 列表 描点 连线
13.且
14.y=x+1
15.
16.
17.1
18.11
19..
20.0
21.(1)1500
(2)12分钟至14分钟;450
(3)4
(4)2700
22.(1)①-3;②略;③略
(2)①函数图象关于y轴对称;②当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大
(3)x≤-1和1≤x
23.(1)自变量是离家时间,因变量是离家的距离
(2)略(答案不唯一)
(3)200米/分钟
(4)略
24.(1)20 km/h;
(2)0.5 h;
(3)30 km.
25.(1)3.2
(2)略
(3)y随x的增大而减小
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在某次数学实验中,测得两个变量x、y间对应的数据如下表:
x 1 2 3 4
y 2.01 4.9 10.03 17.1
则y与x的表达式最接近的是( )
A. B. C. D.
2.下列各曲线中,不是的函数的是( )
A. B.
C. D.
3.汽车由地驶往相距的地,它的平均速度是,则汽车距地路程与行驶时间的关系式为( )
A. B. C. D.
4.如图是甲、乙两车在某时段速度随时间变化的图像;下列说法:
①乙车前 4 秒行驶的路程为 48 米;
②在 0 到 8 秒内甲车的速度每秒增加 4 米;
③两车到第 3 秒时行驶的路程相等;
④在 4 到 8 秒内甲车的速度都大于乙车的速度.
其中正确的有( )
A.1 个 B.2 个 C.3 个 D.4 个
5.如图是加油机上的数据显示牌,其中的变量是( )
A.金额 B.单价 C.油量 D.金额和油量
6.一个直角三角形的两条直角边长的和为20cm,其中一直角边长为xcm,面积为ycm2,则y与x的函数的关系式是( )
A.y=10x﹣x2 B.y=10x C.y=﹣x D.y=x(10﹣x)
7.周末小兰外出爬山,她从山脚爬到山顶的过程中,途中休息了一段时间,设她从山脚出发后所用时间为(分钟),所走路程为(米),与之间的函数关系如图所示,下列说法错误的是( )
A.小兰途中休息了15分钟
B.小兰爬上山顶所走路程为8200米
C.小兰从山脚爬到山顶共用了100分钟
D.小兰休息前的速度大于休息后的速度
8.甲、乙两辆汽车同时分别从相距300千米的A、B两座城市出发相向而行.行驶过程中两车速度不变,甲车到达B城,立即停止,乙车继续行驶,到达A城后停止.若以两车之间的距离为y轴,以两车行驶时间为x轴,画出如图①所示函数图象.若以两车到A城的距离为y轴,以两车行驶时间为x轴在同一坐标体系看画出图象,与图①函数图象意义一致的是( )
A. B. C. D.
9.设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y米,y关于x的函数关系如图所示,则乙车的速度是( )米/秒
A.10 B.15 C.20 D.25
10.梦想从学习开始,事业从实践起步近来,每天登录“学习强国”APP,学精神增能量、看文化、长见识已经成为一种学习新风尚.下面是爸爸上周“学习强国”周积分与学习天数的有关数据,则下列说法错误的是( )
学习天数n(天) 1 2 3 4 5 6 7
周积分w/(分) 55 110 160 200 254 300 350
A.在这个变化过程中,学习天数是自变量,周积分是因变量
B.周积分随学习天数的增加而增加
C.周积分w与学习天数n的关系式为w=50n
D.天数每增加1天,周积分的增长量不一定相同
二、填空题
11.等腰三角形的顶角y与底角x之间是函数关系吗? (是或不是中选择)
12.描点法画函数图象的一般步骤:
第一步: .在自变量取值范围内选定一些值.通过函数关系式求出对应函数值列成表格.
第二步: .在直角坐标系中,以自变量的值为横坐标,相应函数值为纵坐标,描出表中对应各点.
第三步: .按照坐标由小到大的顺序把所有点用平滑曲线连结起来.
13.在函数中,自变量的取值范围是 .
14. (2018年河南省开封市中考模拟考试(4月)) 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角三角形ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,则y与x的解析式是 .
15.函数中,自变量的取值范围为 .
16.由于惯性的作用,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”.
某公司设计了一款新型汽车,需要对它的刹车性能进行测试.设汽车的刹车距离为单位:,车速为单位:,根据测得的数据,与的函数关系如图所示.
(1)若该款汽车某次测试的刹车距离为 ,估计该车的速度约为 ;
(2)在测试中发现该款汽车在车速达到某一数值时,其刹车距离的数值恰好是车速数值的,则此时的车速约为 结果取整数).
17.从A市到B市汽车行驶的高速公路里程固定.假设汽车匀速行驶,汽车行驶的速度v(千米)时)与速度t(小时)的函数图象如图所示.若高速公路的速度限定不超过每小时120千米,则汽车从A市到B市行驶的最短时间为 小时.
18.函数可用表示,例如,当时,,若函数,则的值为 .
19.一个长为120m,宽为100m的矩形场地,要扩建为一个正方形场地,设长增加xm,宽增加ym,则y与x之间的函数关系式为 .
20.对于函数.当x=2时,y= .
三、解答题
21.小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的书店,买到书后继续去学校.如图是他本次上学所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程为________米;
(2)在整个上学途中________时间段小明骑车速度最快,最快的速度是_______米/分;
(3)小明在书店停留了________分钟;
(4)本次上学途中,小明一共行驶了多少米?
22.函数图象是研究函数的重要工具.结合已有的学习函数图象和性质的经验,请画出函数的图象并探究该函数的性质.
(1)绘制函数图象
①列表:下表是中x与y的几组对应值,其中a=______;
x … -4 -3 -2 -1 -0.5 0 0.5 1 2 3 4 …
y … -1 -2 a -2 -1 …
②描点:根据表中的数值描点(x,y),请补充描出点(0,a);
③连线:用平滑的曲线顺次连接各点,请画出函数图象.
(2)探究函数性质:请写出函数的两条性质:①______;②______;
(3)运用函数图象及性质:根据函数图象,写出不等式的解集是______.
23.小李骑自行车从家出发到距离家2000米远的水上公园,如图所示是小李从家到公园路途中离家的距离与离家时间之间关系的图象.
(1)在这个变化过程中,自变量、因变量分别是什么?
(2)观察图象分析,出发后10分钟到15分钟之间可能发生了什么情况?
(3)求这一段骑行中的最高速度是多少?
(4)用自己的语言大致描述小李骑行的情况.
24.小明骑车野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(千米)与小明离家时间x(小时)的函数图象,已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度;
(2)小明在甲地游玩多少时间?
(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.
25.如图,在中,,为边上一动点,,垂足为N.设A,M两点间的距离为xcm(),B,N两点间的距离为ycm(当M点和B点重合时,B,N两点间的距离为0).
小明根据学习函数的经验,对因变量y随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整.
(1)列表:下表的已知数据是根据A,M两点间的距离x进行取点、画图、测量,分别得到的y与x的几组对应值:
x/cm 0 0.5 1 1.5 1.8 2 2.5 3 3.5 4 4.5 5
y/cm 4 3.96 3.79 3.47 a 2.99 2.40 1.79 1.23 0.74 0.33 0
请你通过计算,补全表格: ;
(2)描点、连线:在平面直角坐标系中,描出表中各组数值所对应的点(x,y),并画出y关于x的函数图象;
(3)探究性质:随着自变量x的不断增大,函数y的变化趋势: .
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.B
3.A
4.C
5.D
6.A
7.B
8.D
9.D
10.C
11.是
12. 列表 描点 连线
13.且
14.y=x+1
15.
16.
17.1
18.11
19..
20.0
21.(1)1500
(2)12分钟至14分钟;450
(3)4
(4)2700
22.(1)①-3;②略;③略
(2)①函数图象关于y轴对称;②当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大
(3)x≤-1和1≤x
23.(1)自变量是离家时间,因变量是离家的距离
(2)略(答案不唯一)
(3)200米/分钟
(4)略
24.(1)20 km/h;
(2)0.5 h;
(3)30 km.
25.(1)3.2
(2)略
(3)y随x的增大而减小
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
