江苏省苏州工业园区青剑湖实验中学2023-2024学年八年级上学期数学10月份课堂练习(图片版,无答案)
文档属性
| 名称 | 江苏省苏州工业园区青剑湖实验中学2023-2024学年八年级上学期数学10月份课堂练习(图片版,无答案) | 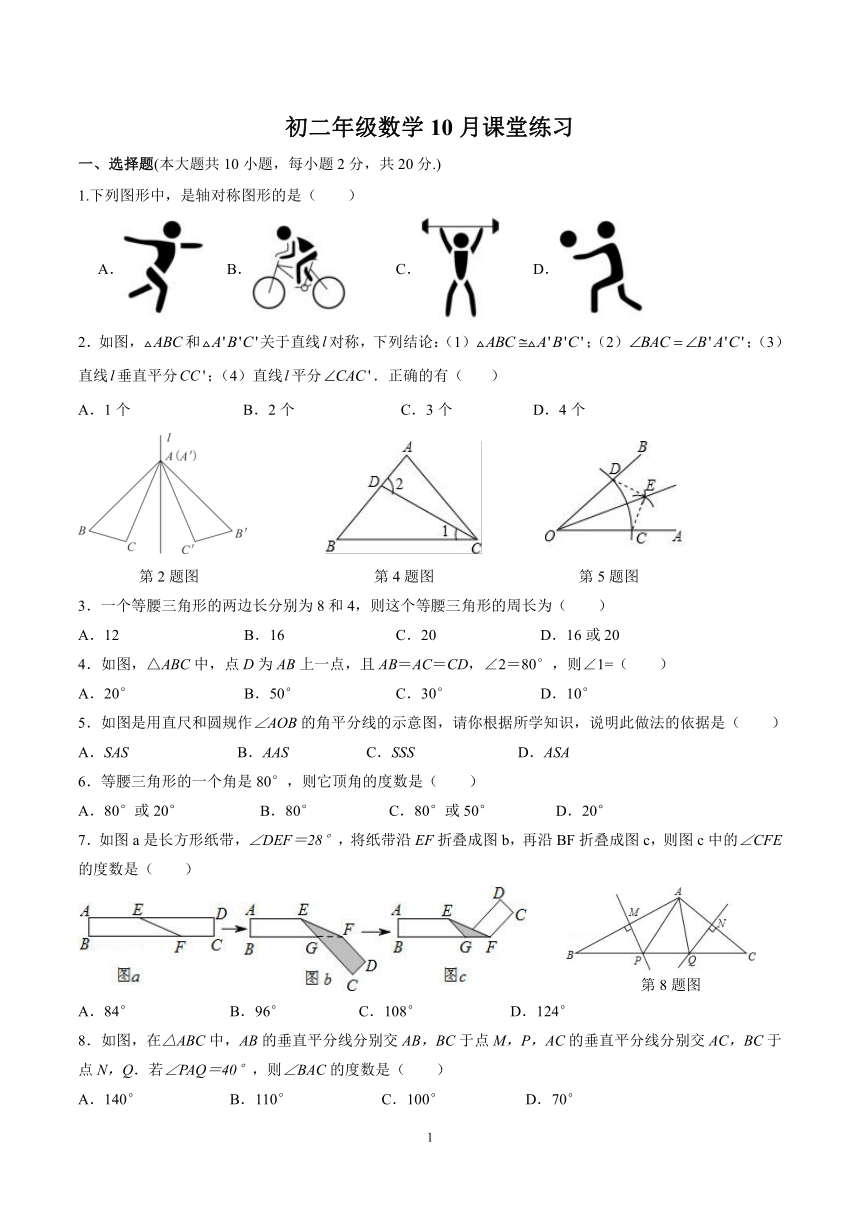 | |
| 格式 | |||
| 文件大小 | 372.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 18:54:45 | ||
图片预览


文档简介
初二年级数学 10 月课堂练习
一、选择题(本大题共 10小题,每小题 2分,共 20分.)
1.下列图形中,是轴对称图形的是( )
A. B. C. D.
2.如图, ABC和 A 'B 'C '关于直线 l对称,下列结论:(1) ABC A 'B 'C ';(2) BAC B 'A 'C ';(3)
直线 l垂直平分CC ';(4)直线 l平分 CAC '.正确的有( )
A.1个 B.2个 C.3个 D.4个
第 2题图 第 4题图 第 5题图
3.一个等腰三角形的两边长分别为 8和 4,则这个等腰三角形的周长为( )
A.12 B.16 C.20 D.16或 20
4.如图,△ABC中,点 D为 AB上一点,且 AB=AC=CD,∠2=80°,则∠1=( )
A.20° B.50° C.30° D.10°
5.如图是用直尺和圆规作∠AOB的角平分线的示意图,请你根据所学知识,说明此做法的依据是( )
A.SAS B.AAS C.SSS D.ASA
6.等腰三角形的一个角是 80°,则它顶角的度数是( )
A.80°或 20° B.80° C.80°或 50° D.20°
7.如图 a是长方形纸带,∠DEF=28°,将纸带沿 EF折叠成图 b,再沿 BF折叠成图 c,则图 c中的∠CFE
的度数是( )
第 8题图
A.84° B.96° C.108° D.124°
8.如图,在△ABC中,AB的垂直平分线分别交 AB,BC于点 M,P,AC的垂直平分线分别交 AC,BC于
点 N,Q.若∠PAQ=40°,则∠BAC的度数是( )
A.140° B.110° C.100° D.70°
1
{#{QQABSQQEgggoABJAAQgCQwXSCACQkAGCAIoGQEAIsAAAQRNABAA=}#}
9.如图,点 P是∠AOB内任意一点,且∠AOB=40°,点 M和点 N分别是射线 OA和射线 OB上的动点,
当△PMN周长取最小值时,则∠MPN的度数为( )
A.140° B.100° C.50° D.40°
第 9题图 第 10题图 第 14题图 第 15题图
10.如图,在△ABC中,AB=AC,∠B=40°,D为线段 BC上一动点(不与 B、C重合),连接 AD,作∠
ADE=40°,DE交线段 AC于点 E.以下四个结论:①∠CDE=∠BAD;②当 D为 BC中点时,DE⊥AC;
③当∠BAD=30°时,BD=CE;④当△ADE为等腰三角形时,∠EDC=30°.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共 8小题,每小题 3分,共 24分).
11.等腰三角形 ABC中,∠A=110°,则∠B= °.
12.已知直角三角形斜边长为 10cm,则此直角三角形斜边上的中线长是 cm.
13.等腰三角形一腰上的高与另一腰的夹角是 20°,则等腰三角形的顶角等于 .
14.如图,在直角三角形纸片 ABC中,∠ACB=90°,∠A=40°,将纸片沿着 CD折叠,使 AC边与 BC
边重合,则∠A′DB的长为 .
15.如图如果点P在射线OC上,PD⊥OA,PE⊥OB,垂足分别为D,E,PD=PE,若∠AOB=40°,∠OPE=______.
16.如图,在四边形 ABCD中,∠ABC=∠ADC=90°,E为对角线 AC的中点,连接 BE,ED,BD.若∠
BAD=56°,则∠EDB的度数为 度.
17.如图,已知:∠BAC的平分线与 BC的垂直平分线相交于点 D,DE⊥AB,DF⊥AC,垂足分别为 E、F,
AB=8,AC=4,则 BE= .
第 16题图 第 17题图 第 18题图
18.如图,∠AOB=60°,C是 BO延长线上的一点,OC=10cm,动点 P从点 C出发沿 CB以 2cm/s的速
度移动,动点 Q从点 O发沿 OA以 1cm/s的速度移动,如果点 P、Q同时出发,用 t(s)表示移动的时间,
当 t= 时,△POQ是等腰三角形.
三、解答题 (本大题共 7小题,共 56分.请在答题卡指定区域内作答)
2
{#{QQABSQQEgggoABJAAQgCQwXSCACQkAGCAIoGQEAIsAAAQRNABAA=}#}
19.(6分)如图,△ABC的顶点 A,B,C都在小正方形的顶点上,利用网格线按下列要求画图.
(1)画△A1B1C1,使它与△ABC关于直线 l成轴对称;
(2)在直线 l上找一点 P,使点 P到点 A,点 B的距离之和最短;
(3)在直线 l上找一点 Q,使点 Q到边 AC,BC的距离相等.
20.(8分)如图,在△ABC中,AB=AC,D为 BC边上一点,∠B=30°,∠DAB=45°.
(1)求∠DAC的度数; (2)求证:DC=AB.
21.(4分)某地有两所大学和两条相交的公路,如图所示(点 M,N表示大学,OA,OB表示公路)现计
划修建一座物资仓库到两所大学的距离相等,到两条公路的距离也相等.请你用尺规确定仓库所在的位置.
23.(8分)如图,锐角三角形 ABC的两条高 BE、CD相交于点 O,且 OB=OC
(1)求证:AB=AC; (2)求证:点 O在∠BAC的平分线上.
24.(10分)如图,在△ABC中,∠B=90°,AB=16cm,BC=12cm,AC=20cm,P、Q是△ABC边上的
两个动点,其中点 P从点 A开始沿 A→B方向运动,且速度为每秒 1cm,点 Q从点 B开始沿 B→C→A
方向运动,且速度为每秒 2cm,它们同时出发,设出发的时间为 t秒.
(1)当点 Q在边 BC上运动时,出发几秒后,△PQB是等腰三角形?
(2)当点 Q在边 CA上运动时,出发几秒后,△BCQ是以 BC或 BQ为底边的等腰三角形?
3
{#{QQABSQQEgggoABJAAQgCQwXSCACQkAGCAIoGQEAIsAAAQRNABAA=}#}
24.(10分)如果一个三角形被一条线段分割成两个等腰三角形,那么这种分割叫做等腰分割,这条线段称
为这个三角形的等腰分割线.如图 1,当△ABD和△ACD为等腰三角形时,AD为△ABC的等腰分割线.
(1)如图 2,△ABC中,∠B=2∠C,线段 AC的垂直平分线 ED交 AC于点 D,交 BC于点 E.求证:AE
是△ABC的一条等腰分割线.
(2)在△ABC中,AD为△ABC的等腰分割线,AD=BD,∠C=30°,请你画出所有可能的图形并求出∠
B的度数.
25.(10分)数学课上,李老师出示了如下的题目:
“在等边三角形 ABC中,点 E在 AB上,点 D在 CB的延长线上,且 ED=EC,如图,试确定线段 AE与
DB的大小关系,并说明理由”.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点 E为 AB的中点时,如图 1,确定线段 AE与 DB的大小关系,请你直接写出结论:
AE__________DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与 DB的大小关系是:AE______________DB(填“>”,“<”或“=”).
理由如下:如图 2,过点 E作 EF∥BC,交 AC于点 F.(请你完成解答过程)
(3)拓展结论,设计新题
在等边三角形 ABC中,点 E在直线 AB上,点 D在直线 BC上,ED=EC.若△ABC的边长为 1,AE=2,
求 CD的长(请你画出图形,并直接写出结果)
F
4
{#{QQABSQQEgggoABJAAQgCQwXSCACQkAGCAIoGQEAIsAAAQRNABAA=}#}
一、选择题(本大题共 10小题,每小题 2分,共 20分.)
1.下列图形中,是轴对称图形的是( )
A. B. C. D.
2.如图, ABC和 A 'B 'C '关于直线 l对称,下列结论:(1) ABC A 'B 'C ';(2) BAC B 'A 'C ';(3)
直线 l垂直平分CC ';(4)直线 l平分 CAC '.正确的有( )
A.1个 B.2个 C.3个 D.4个
第 2题图 第 4题图 第 5题图
3.一个等腰三角形的两边长分别为 8和 4,则这个等腰三角形的周长为( )
A.12 B.16 C.20 D.16或 20
4.如图,△ABC中,点 D为 AB上一点,且 AB=AC=CD,∠2=80°,则∠1=( )
A.20° B.50° C.30° D.10°
5.如图是用直尺和圆规作∠AOB的角平分线的示意图,请你根据所学知识,说明此做法的依据是( )
A.SAS B.AAS C.SSS D.ASA
6.等腰三角形的一个角是 80°,则它顶角的度数是( )
A.80°或 20° B.80° C.80°或 50° D.20°
7.如图 a是长方形纸带,∠DEF=28°,将纸带沿 EF折叠成图 b,再沿 BF折叠成图 c,则图 c中的∠CFE
的度数是( )
第 8题图
A.84° B.96° C.108° D.124°
8.如图,在△ABC中,AB的垂直平分线分别交 AB,BC于点 M,P,AC的垂直平分线分别交 AC,BC于
点 N,Q.若∠PAQ=40°,则∠BAC的度数是( )
A.140° B.110° C.100° D.70°
1
{#{QQABSQQEgggoABJAAQgCQwXSCACQkAGCAIoGQEAIsAAAQRNABAA=}#}
9.如图,点 P是∠AOB内任意一点,且∠AOB=40°,点 M和点 N分别是射线 OA和射线 OB上的动点,
当△PMN周长取最小值时,则∠MPN的度数为( )
A.140° B.100° C.50° D.40°
第 9题图 第 10题图 第 14题图 第 15题图
10.如图,在△ABC中,AB=AC,∠B=40°,D为线段 BC上一动点(不与 B、C重合),连接 AD,作∠
ADE=40°,DE交线段 AC于点 E.以下四个结论:①∠CDE=∠BAD;②当 D为 BC中点时,DE⊥AC;
③当∠BAD=30°时,BD=CE;④当△ADE为等腰三角形时,∠EDC=30°.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共 8小题,每小题 3分,共 24分).
11.等腰三角形 ABC中,∠A=110°,则∠B= °.
12.已知直角三角形斜边长为 10cm,则此直角三角形斜边上的中线长是 cm.
13.等腰三角形一腰上的高与另一腰的夹角是 20°,则等腰三角形的顶角等于 .
14.如图,在直角三角形纸片 ABC中,∠ACB=90°,∠A=40°,将纸片沿着 CD折叠,使 AC边与 BC
边重合,则∠A′DB的长为 .
15.如图如果点P在射线OC上,PD⊥OA,PE⊥OB,垂足分别为D,E,PD=PE,若∠AOB=40°,∠OPE=______.
16.如图,在四边形 ABCD中,∠ABC=∠ADC=90°,E为对角线 AC的中点,连接 BE,ED,BD.若∠
BAD=56°,则∠EDB的度数为 度.
17.如图,已知:∠BAC的平分线与 BC的垂直平分线相交于点 D,DE⊥AB,DF⊥AC,垂足分别为 E、F,
AB=8,AC=4,则 BE= .
第 16题图 第 17题图 第 18题图
18.如图,∠AOB=60°,C是 BO延长线上的一点,OC=10cm,动点 P从点 C出发沿 CB以 2cm/s的速
度移动,动点 Q从点 O发沿 OA以 1cm/s的速度移动,如果点 P、Q同时出发,用 t(s)表示移动的时间,
当 t= 时,△POQ是等腰三角形.
三、解答题 (本大题共 7小题,共 56分.请在答题卡指定区域内作答)
2
{#{QQABSQQEgggoABJAAQgCQwXSCACQkAGCAIoGQEAIsAAAQRNABAA=}#}
19.(6分)如图,△ABC的顶点 A,B,C都在小正方形的顶点上,利用网格线按下列要求画图.
(1)画△A1B1C1,使它与△ABC关于直线 l成轴对称;
(2)在直线 l上找一点 P,使点 P到点 A,点 B的距离之和最短;
(3)在直线 l上找一点 Q,使点 Q到边 AC,BC的距离相等.
20.(8分)如图,在△ABC中,AB=AC,D为 BC边上一点,∠B=30°,∠DAB=45°.
(1)求∠DAC的度数; (2)求证:DC=AB.
21.(4分)某地有两所大学和两条相交的公路,如图所示(点 M,N表示大学,OA,OB表示公路)现计
划修建一座物资仓库到两所大学的距离相等,到两条公路的距离也相等.请你用尺规确定仓库所在的位置.
23.(8分)如图,锐角三角形 ABC的两条高 BE、CD相交于点 O,且 OB=OC
(1)求证:AB=AC; (2)求证:点 O在∠BAC的平分线上.
24.(10分)如图,在△ABC中,∠B=90°,AB=16cm,BC=12cm,AC=20cm,P、Q是△ABC边上的
两个动点,其中点 P从点 A开始沿 A→B方向运动,且速度为每秒 1cm,点 Q从点 B开始沿 B→C→A
方向运动,且速度为每秒 2cm,它们同时出发,设出发的时间为 t秒.
(1)当点 Q在边 BC上运动时,出发几秒后,△PQB是等腰三角形?
(2)当点 Q在边 CA上运动时,出发几秒后,△BCQ是以 BC或 BQ为底边的等腰三角形?
3
{#{QQABSQQEgggoABJAAQgCQwXSCACQkAGCAIoGQEAIsAAAQRNABAA=}#}
24.(10分)如果一个三角形被一条线段分割成两个等腰三角形,那么这种分割叫做等腰分割,这条线段称
为这个三角形的等腰分割线.如图 1,当△ABD和△ACD为等腰三角形时,AD为△ABC的等腰分割线.
(1)如图 2,△ABC中,∠B=2∠C,线段 AC的垂直平分线 ED交 AC于点 D,交 BC于点 E.求证:AE
是△ABC的一条等腰分割线.
(2)在△ABC中,AD为△ABC的等腰分割线,AD=BD,∠C=30°,请你画出所有可能的图形并求出∠
B的度数.
25.(10分)数学课上,李老师出示了如下的题目:
“在等边三角形 ABC中,点 E在 AB上,点 D在 CB的延长线上,且 ED=EC,如图,试确定线段 AE与
DB的大小关系,并说明理由”.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点 E为 AB的中点时,如图 1,确定线段 AE与 DB的大小关系,请你直接写出结论:
AE__________DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与 DB的大小关系是:AE______________DB(填“>”,“<”或“=”).
理由如下:如图 2,过点 E作 EF∥BC,交 AC于点 F.(请你完成解答过程)
(3)拓展结论,设计新题
在等边三角形 ABC中,点 E在直线 AB上,点 D在直线 BC上,ED=EC.若△ABC的边长为 1,AE=2,
求 CD的长(请你画出图形,并直接写出结果)
F
4
{#{QQABSQQEgggoABJAAQgCQwXSCACQkAGCAIoGQEAIsAAAQRNABAA=}#}
同课章节目录
