专题1.1探索勾股定理 知识梳理讲解(含解析)八年级数学上册北师大版基础知识专项突破讲与练
文档属性
| 名称 | 专题1.1探索勾股定理 知识梳理讲解(含解析)八年级数学上册北师大版基础知识专项突破讲与练 |

|
|
| 格式 | docx | ||
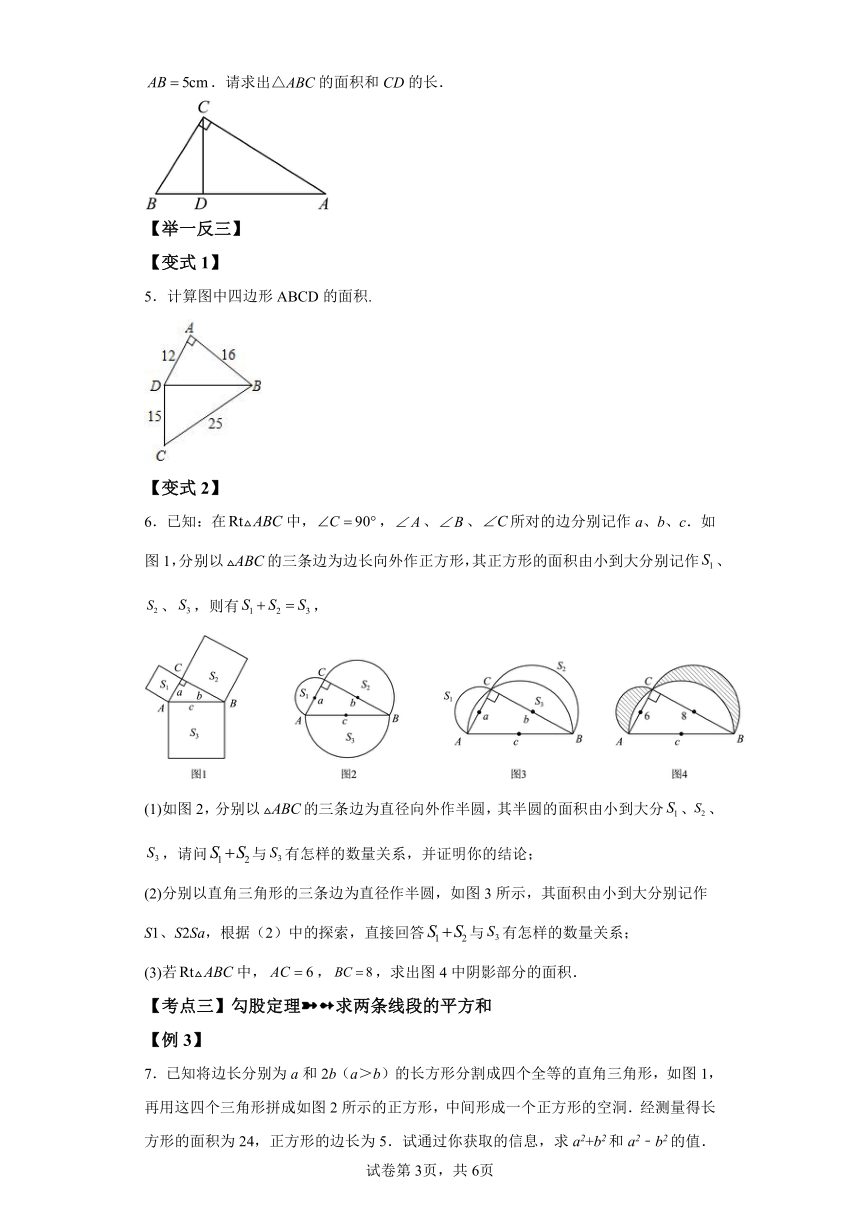
| 文件大小 | 790.7KB | ||
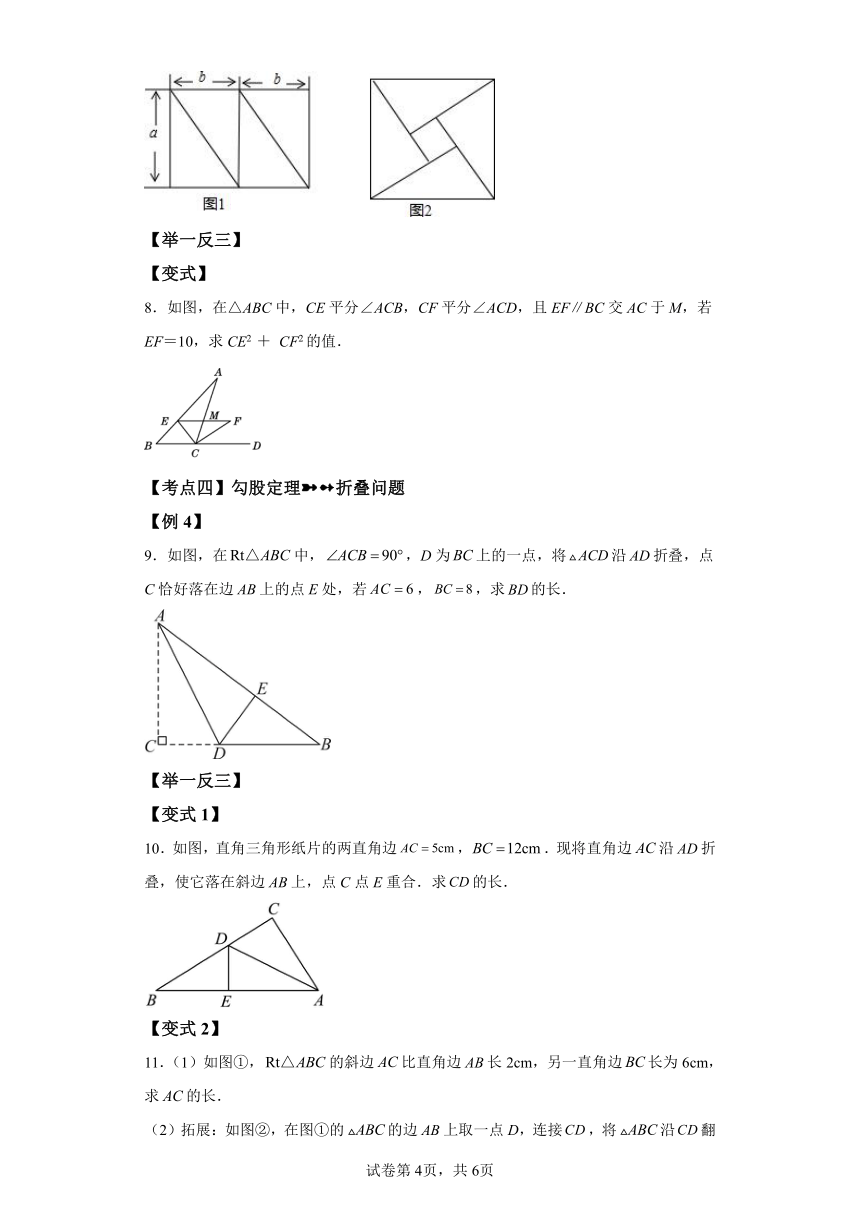
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
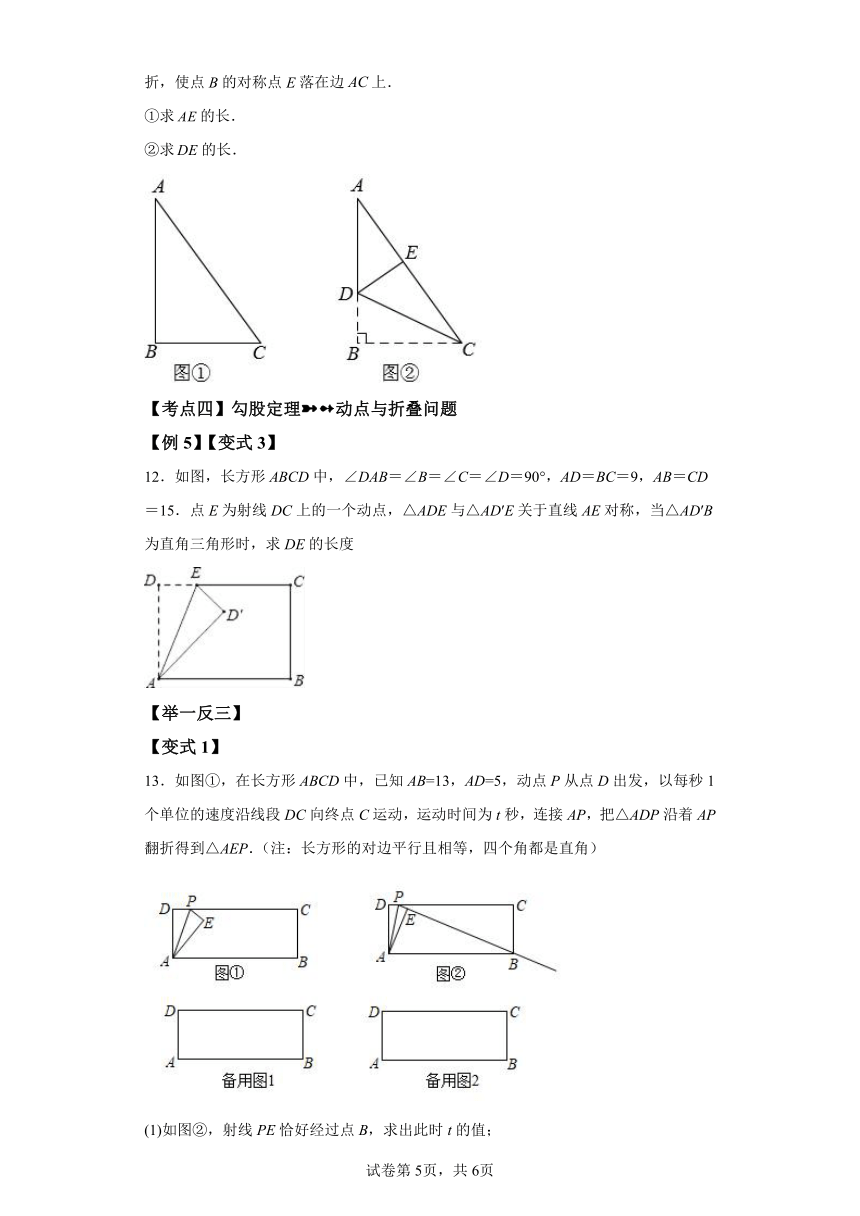
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 00:00:00 | ||
图片预览


文档简介
专题1.1 探索勾股定理(知识梳理与考点分类讲解)
【知识点1】勾股定理
1.定理 直角三角形两直角边的平方和等于斜边的平方,如果有a,b和c分别表示直角三角形的两直角边和斜边,则有
2.变形公式有:;
3.解题的基本思想方法:勾股定理把“形”与“数”有机结合起来,就是把直角三角形中的这个图形的“形”与三边关系这个“数(量)”结合起来,这就是数形结合
【知识点2】勾股定理的证明
1.常用的验证法:验证方法很多,有测量法、几何证明法,但最常用的是通过拼图,构造特殊图形,利用面积等关系进行证明.
2.经典的勾股定理证明方法:
方法一:将四个全等的直角三角形拼成如图(1)所示的正方形.
图(1)中,所以.
方法二:将四个全等的直角三角形拼成如图(2)所示的正方形.
图(2)中,所以.
方法三:如图(3)所示,将两个直角三角形拼成直角梯形.
,所以.
【考点一】勾股定理 求线段长
【例1】
1.如图,嘉嘉在荡秋千时发现,秋千在静止位置时,下端离地面米,荡秋千到位置时,下端距静止位置的水平距离等于米,距地面米,求秋千的长.
【举一反三】
【变式1】
2.如图,在中,,,,求BC边上的高AD的长.
【变式2】
3.如图,在中,,,,于.求:
(1)的长和的面积;
(2)的长.
【考点二】勾股定理 求面积
【例2】
4.如图,在△ABC中,,于点D,,,.请求出△ABC的面积和CD的长.
【举一反三】
【变式1】
5.计算图中四边形ABCD的面积.
【变式2】
6.已知:在中,,、、所对的边分别记作a、b、c.如图1,分别以的三条边为边长向外作正方形,其正方形的面积由小到大分别记作、、,则有,
(1)如图2,分别以的三条边为直径向外作半圆,其半圆的面积由小到大分、、,请问与有怎样的数量关系,并证明你的结论;
(2)分别以直角三角形的三条边为直径作半圆,如图3所示,其面积由小到大分别记作S1、S2Sa,根据(2)中的探索,直接回答与有怎样的数量关系;
(3)若中,,,求出图4中阴影部分的面积.
【考点三】勾股定理 求两条线段的平方和
【例3】
7.已知将边长分别为a和2b(a>b)的长方形分割成四个全等的直角三角形,如图1,再用这四个三角形拼成如图2所示的正方形,中间形成一个正方形的空洞.经测量得长方形的面积为24,正方形的边长为5.试通过你获取的信息,求a2+b2和a2﹣b2的值.
【举一反三】
【变式】
8.如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若EF=10,求CE2 + CF2的值.
【考点四】勾股定理 折叠问题
【例4】
9.如图,在中,,D为上的一点,将沿折叠,点C恰好落在边上的点E处,若,,求的长.
【举一反三】
【变式1】
10.如图,直角三角形纸片的两直角边,.现将直角边沿折叠,使它落在斜边上,点C点E重合.求的长.
【变式2】
11.(1)如图①,的斜边比直角边长2cm,另一直角边长为6cm,求的长.
(2)拓展:如图②,在图①的的边上取一点D,连接,将沿翻折,使点B的对称点E落在边上.
①求的长.
②求的长.
【考点四】勾股定理 动点与折叠问题
【例5】【变式3】
12.如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=9,AB=CD=15.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,求DE的长度
【举一反三】
【变式1】
13.如图①,在长方形ABCD中,已知AB=13,AD=5,动点P从点D出发,以每秒1个单位的速度沿线段DC向终点C运动,运动时间为t秒,连接AP,把△ADP沿着AP翻折得到△AEP.(注:长方形的对边平行且相等,四个角都是直角)
(1)如图②,射线PE恰好经过点B,求出此时t的值;
(2)当射线PE与边AB交于点F时,是否存在这样的t的值,使得FE=FB?若存在,请求出所有符合题意的t的值;若不存在,请说明理由;
(3)在动点P从点D到点C的整个运动过程中,若点E到直线AB的距离等于3,则此时t=___________.
【变式2】
14.在矩形ABCD中,AB=6,BC=8,点E是射线BC上一个动点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折到△AB'E,延长AB'与直线CD交于点M.
(1)求证:AM=MF;
(2)当点E是边BC的中点时,求CM的长;
(3)当CF=4时,求CM的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.米
【分析】根据题意,设为米,在中,根据勾股定理即可求解.
【详解】解:如图所示,
根据题意可知:,
设为米,
∴,
∴,
∵,
∴,
在中,
∴,
∴,
∴,
∴秋千的长为米.
【点睛】本题主要考查直角三角形的勾股定理,掌握勾股定理的计算方法是解题的关键.
2.12
【分析】为高,那么题中有两个直角三角形.在这两个直角三角形中,设为未知数,可利用勾股定理都表示出长.求得长,再根据勾股定理求得长即可.
【详解】解:设,则,
在中,,
在中,,
∴,
,
解得,
在中,.
【点睛】本题考查了勾股定理,解决本题的关键在于利用两个直角三角形的公共边找到突破点.主要利用了勾股定理进行解答.
3.(1),
(2)
【分析】(1)根据勾股定理求得的长;利用三角形的面积公式可求出的面积;
(2)再根据三角形的面积公式是一定值求得即可.
【详解】(1)解:在中,,,,
∴,
∴.
(2)解:,
,
.
【点睛】此题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解题的关键.
4.△ABC的面积为,CD的长为cm
【分析】根据直角三角形面积公式即可求解三角形的面积,再根据直角三角形面积的两种计算方法求出斜边上的高.
【详解】解:∵∠ACB=90
∴
∵
∴
∴
答:△ABC的面积为,CD的长为cm.
【点睛】本题考查直角三角形的性质及其面积公式,解题的关键是熟知三角形面积不变.
5.246
【分析】根据观察图形可以看出四边形ABCD的面积为△ABD和△BCD的面积之和,根据AD,AB可以计算△ABD的面积和BD的长,根据CD,BD可以计算△BCD的面积,即可解题.
【详解】解:在Rt△ABD中,BD为斜边,
AD=12,AB=16,
则BD=,
故四边形ABCD的面积为S△ABD+S△BCD=×12×16+×15×20=96+150=246.
答:四边形ABCD的面积为246.
【点睛】本题考查了勾股定理在直角三角形中的运用,考查了直角三角形面积计算方法,本题中正确的计算△ABD和△BCD的面积是解题的关键.
6.(1),证明见解析
(2)
(3)24
【分析】(1)由扇形的面积公式可知,,,在Rt△ABC中,由勾股定理得AC2+BC2=AB2,即S1+S2=S3;
(2)根据(1)中的求解即可得出答案;
(3)利用(2)中的结论进行求解.
【详解】(1)解:①,
根据勾股定理可知:,
;
(2)解:由(1)知,同理根据根据勾股定理:,从而可得;
(3)解:由(2)知.
【点睛】本题考查勾股定理的应用,解题关键是对勾股定理的熟练掌握及灵活运用.
7.a2+b2=25,a2﹣b2=7.
【分析】根据勾股定理,长方形的面积为24,正方形的面积计算方法,列出关于a、b方程组,然后求解.
【详解】解:根据题意得
a2+b2=52=25,
a 2b=24,
∴a2+b2+2ab=49,
∴a+b=7,
由图2得(a-b)2=52-24=1,
∵a>b,
∴a-b=1,
∴a2﹣b2=(a+b)(a-b)=7×1=7,
∴a2+b2=25,a2﹣b2=7.
【点睛】本题考查勾股定理、正方形的性质及直角三角形.解题的关键是根据图示找出大正方形、四个直角三角形、小正方形间的数量关系.
8.100
【分析】根据角平分线的定义推知∠ECF=90°,然后在直角三角形ECF中利用勾股定理求CE2+CF2的值即可.
【详解】解:∵ B、C、D三点在一条直线上,CE平分∠ACB,CF平分∠ACD,
∴∠ECF=∠ECA+∠FCA=∠ACB+∠ACD=×180°=90°.
∴CE2 + CF2=EF2 .
∵EF=10,
∴CE2+CF2=102=100.
【点睛】本题考查勾股定理, 角平分线线的性质.
9.
【分析】根据折叠的性质可得,,,设,则,在中,,列方程求解即可.
【详解】在中,,,,
由折叠性质可知,
,,,
∴,
设,则,
在中,,
∴,
解得,
∴.
【点睛】本题考查了折叠问题以及勾股定理,运用折叠的性质以及勾股定理列方程求解是本题的关键.
10.CD的长为.
【分析】根据勾股定理求得的长,再根据折叠的性质求得的长,从而利用勾股定理可求得的长.
【详解】解:∵,,
∴,
由折叠的性质得,,
∴,
设,则在中,,
∴.
答:的长为.
【点睛】本题考查了折叠的性质以及利用勾股定理解直角三角形的能力,即:直角三角形两直角边的平方和等于斜边的平方.
11.(1)10cm;(2)① 4cm;② 3cm
【分析】(1)利用勾股定理,进行求解即可;
(2)①根据翻折得到,利用求出的长即可;
②在中,利用勾股定理进行求解即可.
【详解】解:(1)设,则,
在中:,即:,
解得:;
∴;
(2)①∵将沿翻折,使点B的对称点E落在边上,
∴,
∴;
②∵将沿翻折,使点B的对称点E落在边上,
∴,
设,则,
在中:,即:,
解得:;
即:.
【点睛】本题考查勾股定理与折叠问题.熟练掌握折叠的性质,对应边相等,对应角相等,以及勾股定理,是解题的关键.
12.DE=3或27.
【分析】分两种情况:点E在DC线段上,点E为DC延长线上的一点,进一步分析探讨得出答案即可.
【详解】如图1,
∵折叠,
∴△AD′E≌△ADE,
∴∠AD′E=∠D=90°,AD′=AD,
∵∠AD′B=90°,
∴B、D′、E三点共线,
∵∠ABD′=∠BEC,∠AD′B=∠C=90°,AD′=BC,
∴ABD′≌△BEC,
∴BE=AB=15,
∵BD′===12,
∴DE=D′E=15﹣12=3;
如图2,
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
,
∴△ABD″≌△BEC,
∴BE=AB=15,
∴DE=D″E=15+12=27.
综上所知,DE=3或27.
【点睛】此题考查翻折的性质,三角形全等的判定与性质,勾股定理,掌握翻折的性质,分类探讨的思想方法是解决问题的关键.
13.(1)1
(2)或13
(3)或10
【分析】(1)由长方形性质得知,,,,再证,则,然后由勾股定理得,则,由此得出结论.
(2)分两种情况:E在矩形内部和外部两种情况,分别根据等量关系列出方程即可解答.
(3)分两种情况:E在AB上方和下方两种情况,由折叠性质与勾股定理即可解答.
【详解】(1) 四边形ABCD是长方形,
,,,,
,
由翻折性质可知:,
,
在中,由勾股定理得:
,
,
,
.
(2)存在,分两种情况:
如图③,当点E在长方形内部时:
作于G,设,则
由翻折可知,,
在中,由勾股定理可得:,即 ,
解得:,即,
在与 中:
,解得:.
如图④,当点P运动至与点C重合时,在与中:
,
.
综上,当或时,有.
(3)过点E作交AB于点M,交CD于点N.
如图⑤,点E在长方形内部: 则,
在中,由勾股定理得:
在中,由勾股定理得:
,即
解得:
如图⑥,点E在长方形外部:则,
在中,由勾股定理得:
在中,由勾股定理得:
,即
解得:
综上,若点E到直线AB的距离等于3,或.
【点睛】本题是几何综合题目,考查了轴对称的性质、勾股定理、等腰三角形的判定等知识,综合性强,熟练掌握轴对称的性质及勾股定理,进行分类讨论解题是本题的解题关键.
14.(1)见解析
(2)
(3)或 21
【分析】(1)由折叠的性质及等腰三角形的判定可得出答案;
(2)利用矩形的性质证得,根据全等三角形的性质得到,设,则由(1)知,, ,在中利用勾股定理即可求解;
(3)当时,设,应分两种情况:第一种情况,点在线段上,如图所示,则,;
第二种情况,点在线段上,如图所示,则,
在中,利用勾股定理即可求解.
【详解】(1)证明:∵四边形ABCD为矩形,
∴ABCD,
∴∠F=∠BAF,
由折叠可知:∠BAF=∠MAF,
∴∠F=∠MAF,
∴AM=MF;
(2)∵点E是边BC的中点,
∴,
∵四边形ABCD为矩形,,
∴ABCD,,
∴∠F=∠BAF,
又∵,
∴,
∴,
设,则由(1)知,,
在中,,
∴,
解得,
∴的长为;
(3)当时,设,应分两种情况:
第一种情况,点在线段上,如图所示,则,
∴在中,,
∴,
解得,
∴的长为;
第二种情况,点在线段的延长线上,如图所示,则,
∴在中,,
∴,解得,
∴的长为
综上可知,当CF=4时,CM的长为或 21
【点睛】本题考查了翻折变换,矩形的性质,勾股定理等知识,分类讨论的思想是解题的关键.
答案第1页,共2页
答案第1页,共2页
【知识点1】勾股定理
1.定理 直角三角形两直角边的平方和等于斜边的平方,如果有a,b和c分别表示直角三角形的两直角边和斜边,则有
2.变形公式有:;
3.解题的基本思想方法:勾股定理把“形”与“数”有机结合起来,就是把直角三角形中的这个图形的“形”与三边关系这个“数(量)”结合起来,这就是数形结合
【知识点2】勾股定理的证明
1.常用的验证法:验证方法很多,有测量法、几何证明法,但最常用的是通过拼图,构造特殊图形,利用面积等关系进行证明.
2.经典的勾股定理证明方法:
方法一:将四个全等的直角三角形拼成如图(1)所示的正方形.
图(1)中,所以.
方法二:将四个全等的直角三角形拼成如图(2)所示的正方形.
图(2)中,所以.
方法三:如图(3)所示,将两个直角三角形拼成直角梯形.
,所以.
【考点一】勾股定理 求线段长
【例1】
1.如图,嘉嘉在荡秋千时发现,秋千在静止位置时,下端离地面米,荡秋千到位置时,下端距静止位置的水平距离等于米,距地面米,求秋千的长.
【举一反三】
【变式1】
2.如图,在中,,,,求BC边上的高AD的长.
【变式2】
3.如图,在中,,,,于.求:
(1)的长和的面积;
(2)的长.
【考点二】勾股定理 求面积
【例2】
4.如图,在△ABC中,,于点D,,,.请求出△ABC的面积和CD的长.
【举一反三】
【变式1】
5.计算图中四边形ABCD的面积.
【变式2】
6.已知:在中,,、、所对的边分别记作a、b、c.如图1,分别以的三条边为边长向外作正方形,其正方形的面积由小到大分别记作、、,则有,
(1)如图2,分别以的三条边为直径向外作半圆,其半圆的面积由小到大分、、,请问与有怎样的数量关系,并证明你的结论;
(2)分别以直角三角形的三条边为直径作半圆,如图3所示,其面积由小到大分别记作S1、S2Sa,根据(2)中的探索,直接回答与有怎样的数量关系;
(3)若中,,,求出图4中阴影部分的面积.
【考点三】勾股定理 求两条线段的平方和
【例3】
7.已知将边长分别为a和2b(a>b)的长方形分割成四个全等的直角三角形,如图1,再用这四个三角形拼成如图2所示的正方形,中间形成一个正方形的空洞.经测量得长方形的面积为24,正方形的边长为5.试通过你获取的信息,求a2+b2和a2﹣b2的值.
【举一反三】
【变式】
8.如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若EF=10,求CE2 + CF2的值.
【考点四】勾股定理 折叠问题
【例4】
9.如图,在中,,D为上的一点,将沿折叠,点C恰好落在边上的点E处,若,,求的长.
【举一反三】
【变式1】
10.如图,直角三角形纸片的两直角边,.现将直角边沿折叠,使它落在斜边上,点C点E重合.求的长.
【变式2】
11.(1)如图①,的斜边比直角边长2cm,另一直角边长为6cm,求的长.
(2)拓展:如图②,在图①的的边上取一点D,连接,将沿翻折,使点B的对称点E落在边上.
①求的长.
②求的长.
【考点四】勾股定理 动点与折叠问题
【例5】【变式3】
12.如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=9,AB=CD=15.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,求DE的长度
【举一反三】
【变式1】
13.如图①,在长方形ABCD中,已知AB=13,AD=5,动点P从点D出发,以每秒1个单位的速度沿线段DC向终点C运动,运动时间为t秒,连接AP,把△ADP沿着AP翻折得到△AEP.(注:长方形的对边平行且相等,四个角都是直角)
(1)如图②,射线PE恰好经过点B,求出此时t的值;
(2)当射线PE与边AB交于点F时,是否存在这样的t的值,使得FE=FB?若存在,请求出所有符合题意的t的值;若不存在,请说明理由;
(3)在动点P从点D到点C的整个运动过程中,若点E到直线AB的距离等于3,则此时t=___________.
【变式2】
14.在矩形ABCD中,AB=6,BC=8,点E是射线BC上一个动点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折到△AB'E,延长AB'与直线CD交于点M.
(1)求证:AM=MF;
(2)当点E是边BC的中点时,求CM的长;
(3)当CF=4时,求CM的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.米
【分析】根据题意,设为米,在中,根据勾股定理即可求解.
【详解】解:如图所示,
根据题意可知:,
设为米,
∴,
∴,
∵,
∴,
在中,
∴,
∴,
∴,
∴秋千的长为米.
【点睛】本题主要考查直角三角形的勾股定理,掌握勾股定理的计算方法是解题的关键.
2.12
【分析】为高,那么题中有两个直角三角形.在这两个直角三角形中,设为未知数,可利用勾股定理都表示出长.求得长,再根据勾股定理求得长即可.
【详解】解:设,则,
在中,,
在中,,
∴,
,
解得,
在中,.
【点睛】本题考查了勾股定理,解决本题的关键在于利用两个直角三角形的公共边找到突破点.主要利用了勾股定理进行解答.
3.(1),
(2)
【分析】(1)根据勾股定理求得的长;利用三角形的面积公式可求出的面积;
(2)再根据三角形的面积公式是一定值求得即可.
【详解】(1)解:在中,,,,
∴,
∴.
(2)解:,
,
.
【点睛】此题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解题的关键.
4.△ABC的面积为,CD的长为cm
【分析】根据直角三角形面积公式即可求解三角形的面积,再根据直角三角形面积的两种计算方法求出斜边上的高.
【详解】解:∵∠ACB=90
∴
∵
∴
∴
答:△ABC的面积为,CD的长为cm.
【点睛】本题考查直角三角形的性质及其面积公式,解题的关键是熟知三角形面积不变.
5.246
【分析】根据观察图形可以看出四边形ABCD的面积为△ABD和△BCD的面积之和,根据AD,AB可以计算△ABD的面积和BD的长,根据CD,BD可以计算△BCD的面积,即可解题.
【详解】解:在Rt△ABD中,BD为斜边,
AD=12,AB=16,
则BD=,
故四边形ABCD的面积为S△ABD+S△BCD=×12×16+×15×20=96+150=246.
答:四边形ABCD的面积为246.
【点睛】本题考查了勾股定理在直角三角形中的运用,考查了直角三角形面积计算方法,本题中正确的计算△ABD和△BCD的面积是解题的关键.
6.(1),证明见解析
(2)
(3)24
【分析】(1)由扇形的面积公式可知,,,在Rt△ABC中,由勾股定理得AC2+BC2=AB2,即S1+S2=S3;
(2)根据(1)中的求解即可得出答案;
(3)利用(2)中的结论进行求解.
【详解】(1)解:①,
根据勾股定理可知:,
;
(2)解:由(1)知,同理根据根据勾股定理:,从而可得;
(3)解:由(2)知.
【点睛】本题考查勾股定理的应用,解题关键是对勾股定理的熟练掌握及灵活运用.
7.a2+b2=25,a2﹣b2=7.
【分析】根据勾股定理,长方形的面积为24,正方形的面积计算方法,列出关于a、b方程组,然后求解.
【详解】解:根据题意得
a2+b2=52=25,
a 2b=24,
∴a2+b2+2ab=49,
∴a+b=7,
由图2得(a-b)2=52-24=1,
∵a>b,
∴a-b=1,
∴a2﹣b2=(a+b)(a-b)=7×1=7,
∴a2+b2=25,a2﹣b2=7.
【点睛】本题考查勾股定理、正方形的性质及直角三角形.解题的关键是根据图示找出大正方形、四个直角三角形、小正方形间的数量关系.
8.100
【分析】根据角平分线的定义推知∠ECF=90°,然后在直角三角形ECF中利用勾股定理求CE2+CF2的值即可.
【详解】解:∵ B、C、D三点在一条直线上,CE平分∠ACB,CF平分∠ACD,
∴∠ECF=∠ECA+∠FCA=∠ACB+∠ACD=×180°=90°.
∴CE2 + CF2=EF2 .
∵EF=10,
∴CE2+CF2=102=100.
【点睛】本题考查勾股定理, 角平分线线的性质.
9.
【分析】根据折叠的性质可得,,,设,则,在中,,列方程求解即可.
【详解】在中,,,,
由折叠性质可知,
,,,
∴,
设,则,
在中,,
∴,
解得,
∴.
【点睛】本题考查了折叠问题以及勾股定理,运用折叠的性质以及勾股定理列方程求解是本题的关键.
10.CD的长为.
【分析】根据勾股定理求得的长,再根据折叠的性质求得的长,从而利用勾股定理可求得的长.
【详解】解:∵,,
∴,
由折叠的性质得,,
∴,
设,则在中,,
∴.
答:的长为.
【点睛】本题考查了折叠的性质以及利用勾股定理解直角三角形的能力,即:直角三角形两直角边的平方和等于斜边的平方.
11.(1)10cm;(2)① 4cm;② 3cm
【分析】(1)利用勾股定理,进行求解即可;
(2)①根据翻折得到,利用求出的长即可;
②在中,利用勾股定理进行求解即可.
【详解】解:(1)设,则,
在中:,即:,
解得:;
∴;
(2)①∵将沿翻折,使点B的对称点E落在边上,
∴,
∴;
②∵将沿翻折,使点B的对称点E落在边上,
∴,
设,则,
在中:,即:,
解得:;
即:.
【点睛】本题考查勾股定理与折叠问题.熟练掌握折叠的性质,对应边相等,对应角相等,以及勾股定理,是解题的关键.
12.DE=3或27.
【分析】分两种情况:点E在DC线段上,点E为DC延长线上的一点,进一步分析探讨得出答案即可.
【详解】如图1,
∵折叠,
∴△AD′E≌△ADE,
∴∠AD′E=∠D=90°,AD′=AD,
∵∠AD′B=90°,
∴B、D′、E三点共线,
∵∠ABD′=∠BEC,∠AD′B=∠C=90°,AD′=BC,
∴ABD′≌△BEC,
∴BE=AB=15,
∵BD′===12,
∴DE=D′E=15﹣12=3;
如图2,
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
,
∴△ABD″≌△BEC,
∴BE=AB=15,
∴DE=D″E=15+12=27.
综上所知,DE=3或27.
【点睛】此题考查翻折的性质,三角形全等的判定与性质,勾股定理,掌握翻折的性质,分类探讨的思想方法是解决问题的关键.
13.(1)1
(2)或13
(3)或10
【分析】(1)由长方形性质得知,,,,再证,则,然后由勾股定理得,则,由此得出结论.
(2)分两种情况:E在矩形内部和外部两种情况,分别根据等量关系列出方程即可解答.
(3)分两种情况:E在AB上方和下方两种情况,由折叠性质与勾股定理即可解答.
【详解】(1) 四边形ABCD是长方形,
,,,,
,
由翻折性质可知:,
,
在中,由勾股定理得:
,
,
,
.
(2)存在,分两种情况:
如图③,当点E在长方形内部时:
作于G,设,则
由翻折可知,,
在中,由勾股定理可得:,即 ,
解得:,即,
在与 中:
,解得:.
如图④,当点P运动至与点C重合时,在与中:
,
.
综上,当或时,有.
(3)过点E作交AB于点M,交CD于点N.
如图⑤,点E在长方形内部: 则,
在中,由勾股定理得:
在中,由勾股定理得:
,即
解得:
如图⑥,点E在长方形外部:则,
在中,由勾股定理得:
在中,由勾股定理得:
,即
解得:
综上,若点E到直线AB的距离等于3,或.
【点睛】本题是几何综合题目,考查了轴对称的性质、勾股定理、等腰三角形的判定等知识,综合性强,熟练掌握轴对称的性质及勾股定理,进行分类讨论解题是本题的解题关键.
14.(1)见解析
(2)
(3)或 21
【分析】(1)由折叠的性质及等腰三角形的判定可得出答案;
(2)利用矩形的性质证得,根据全等三角形的性质得到,设,则由(1)知,, ,在中利用勾股定理即可求解;
(3)当时,设,应分两种情况:第一种情况,点在线段上,如图所示,则,;
第二种情况,点在线段上,如图所示,则,
在中,利用勾股定理即可求解.
【详解】(1)证明:∵四边形ABCD为矩形,
∴ABCD,
∴∠F=∠BAF,
由折叠可知:∠BAF=∠MAF,
∴∠F=∠MAF,
∴AM=MF;
(2)∵点E是边BC的中点,
∴,
∵四边形ABCD为矩形,,
∴ABCD,,
∴∠F=∠BAF,
又∵,
∴,
∴,
设,则由(1)知,,
在中,,
∴,
解得,
∴的长为;
(3)当时,设,应分两种情况:
第一种情况,点在线段上,如图所示,则,
∴在中,,
∴,
解得,
∴的长为;
第二种情况,点在线段的延长线上,如图所示,则,
∴在中,,
∴,解得,
∴的长为
综上可知,当CF=4时,CM的长为或 21
【点睛】本题考查了翻折变换,矩形的性质,勾股定理等知识,分类讨论的思想是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
