用列举法求概率(湖北省武汉市硚口区)
文档属性
| 名称 | 用列举法求概率(湖北省武汉市硚口区) |
|
|
| 格式 | rar | ||
| 文件大小 | 14.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-12 00:00:00 | ||
图片预览

文档简介
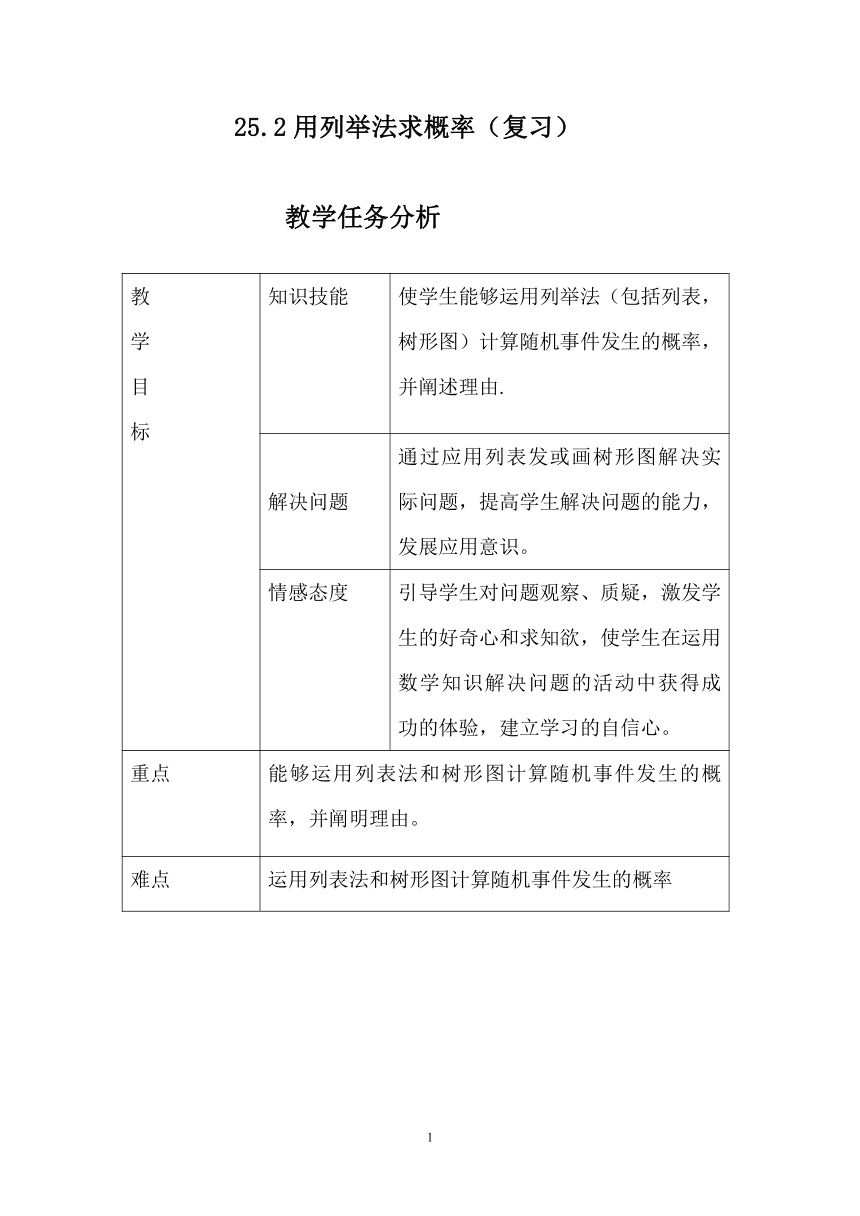
25.2用列举法求概率(复习)
教学任务分析
教学目标 知识技能 使学生能够运用列举法(包括列表,树形图)计算随机事件发生的概率,并阐述理由.
解决问题 通过应用列表发或画树形图解决实际问题,提高学生解决问题的能力,发展应用意识。
情感态度 引导学生对问题观察、质疑,激发学生的好奇心和求知欲,使学生在运用数学知识解决问题的活动中获得成功的体验,建立学习的自信心。
重点 能够运用列表法和树形图计算随机事件发生的概率,并阐明理由。
难点 运用列表法和树形图计算随机事件发生的概率
教学过程设计
问题与情境 师生行为 设计意图
活动1:如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).游戏规则是:如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率. 教师准备教具,学生上来摸球。教师提问:能否用所学的知识计算游戏者获胜的概率呢?学生计算,并演板。每次游戏时,所有可能出现的结果如下:1231(1,1)(1,2)(1,3)2(1,2)(2,2)(3,2)总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有一种:(1,1),因此游戏者获胜的概率为1/6. 通过游戏方式,激发学生学习兴趣,并复习列表法,和树形图求概率。
活动2:想一想小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形。游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色1)利用树形图或列表的方法表示游戏者所有可能出现的结果.(2)游戏者获胜的概率是多少 学生思考后解答:当一个事件要涉及两个因素并且可能出现的结果数目较多时,为不重不漏地列出所有可能地结果,通常采用列表法(或树形图)。计算出概率为1/6. 让学生回顾在具体情境中运用列举法计算简单事件的方法。
活动3:做一做“配紫色”游戏的变异用如图所示的转盘进行“配紫色”游戏,概率是否依然为1/6 学生思考后解答:分析:转动B盘,蓝,黄,绿出现的可能性不同,因此不能采用上题中的做法。将黄色分为两部分,记为黄1,黄2;蓝色分为三部分,记为蓝1,蓝2,蓝3;列表应为:黄1黄2蓝1蓝2蓝3绿红色红,黄红,黄红,蓝红,蓝红,蓝红,绿白色白,黄白,黄白,蓝白,蓝白,蓝白,绿概率应为1/4。 通过对较为复杂地概率问题地探索,激发学生的学习兴趣。
活动4:设计两个转盘做“配紫色”游戏,使游戏者获胜的概率为1/3 学生分组设计,教师巡视,指导。 培养学生学以致用的数学思想,培养团结合作的互助思想。
活动5:有一种转盘游戏,你只要出0.5元钱就可以随意转动转盘,转盘停止时指针落在哪个区域,你就按照这个区域所示的数字相应的顺时针跳过几格,然后按照下图所示的说明确定你的奖金是多少。例如,当指针指向“2”区域的时候,你就向前跳过两个格到“5”,按奖金说明,“5”所示的奖金为0.3元,你就可以得到0.3元。你会去玩这个游戏吗?能否用你所学的知识揭示其中的秘密? “1” 0.1元“2” 0.5元 “3” 0.2元 “4” 10元 “5” 0.3元 “6” 5元 我们可以用列举法求每种情况的概率。因为转盘是六等分的,因此指针指向每个数字的机会均等,但最后跳到的数字只有1,3,5。因此本题中,最终得到1,3,5奖的概率各为1/3,而得到2,4,6奖的概率全部为0。1,3,5奖都是低于0.5元的低额奖金,2,4,6奖金高,但根本无法得到。所以这是个骗局。指针指向的数字最后跳到的数字132531435561 培养学生应用数学的能力,用科学知识辨别真伪的意识。
活动6:归纳总结与作业1、这节课你学到了什么?2、作业:P171复习题4, 5题. 学生自己总结发言,不足之处由其他学生补充完善,教师重点关注不同层次的学生对知识的理解,掌握程度。 了解教学效果,及时调整教学。
PAGE
1
教学任务分析
教学目标 知识技能 使学生能够运用列举法(包括列表,树形图)计算随机事件发生的概率,并阐述理由.
解决问题 通过应用列表发或画树形图解决实际问题,提高学生解决问题的能力,发展应用意识。
情感态度 引导学生对问题观察、质疑,激发学生的好奇心和求知欲,使学生在运用数学知识解决问题的活动中获得成功的体验,建立学习的自信心。
重点 能够运用列表法和树形图计算随机事件发生的概率,并阐明理由。
难点 运用列表法和树形图计算随机事件发生的概率
教学过程设计
问题与情境 师生行为 设计意图
活动1:如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).游戏规则是:如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率. 教师准备教具,学生上来摸球。教师提问:能否用所学的知识计算游戏者获胜的概率呢?学生计算,并演板。每次游戏时,所有可能出现的结果如下:1231(1,1)(1,2)(1,3)2(1,2)(2,2)(3,2)总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有一种:(1,1),因此游戏者获胜的概率为1/6. 通过游戏方式,激发学生学习兴趣,并复习列表法,和树形图求概率。
活动2:想一想小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形。游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色1)利用树形图或列表的方法表示游戏者所有可能出现的结果.(2)游戏者获胜的概率是多少 学生思考后解答:当一个事件要涉及两个因素并且可能出现的结果数目较多时,为不重不漏地列出所有可能地结果,通常采用列表法(或树形图)。计算出概率为1/6. 让学生回顾在具体情境中运用列举法计算简单事件的方法。
活动3:做一做“配紫色”游戏的变异用如图所示的转盘进行“配紫色”游戏,概率是否依然为1/6 学生思考后解答:分析:转动B盘,蓝,黄,绿出现的可能性不同,因此不能采用上题中的做法。将黄色分为两部分,记为黄1,黄2;蓝色分为三部分,记为蓝1,蓝2,蓝3;列表应为:黄1黄2蓝1蓝2蓝3绿红色红,黄红,黄红,蓝红,蓝红,蓝红,绿白色白,黄白,黄白,蓝白,蓝白,蓝白,绿概率应为1/4。 通过对较为复杂地概率问题地探索,激发学生的学习兴趣。
活动4:设计两个转盘做“配紫色”游戏,使游戏者获胜的概率为1/3 学生分组设计,教师巡视,指导。 培养学生学以致用的数学思想,培养团结合作的互助思想。
活动5:有一种转盘游戏,你只要出0.5元钱就可以随意转动转盘,转盘停止时指针落在哪个区域,你就按照这个区域所示的数字相应的顺时针跳过几格,然后按照下图所示的说明确定你的奖金是多少。例如,当指针指向“2”区域的时候,你就向前跳过两个格到“5”,按奖金说明,“5”所示的奖金为0.3元,你就可以得到0.3元。你会去玩这个游戏吗?能否用你所学的知识揭示其中的秘密? “1” 0.1元“2” 0.5元 “3” 0.2元 “4” 10元 “5” 0.3元 “6” 5元 我们可以用列举法求每种情况的概率。因为转盘是六等分的,因此指针指向每个数字的机会均等,但最后跳到的数字只有1,3,5。因此本题中,最终得到1,3,5奖的概率各为1/3,而得到2,4,6奖的概率全部为0。1,3,5奖都是低于0.5元的低额奖金,2,4,6奖金高,但根本无法得到。所以这是个骗局。指针指向的数字最后跳到的数字132531435561 培养学生应用数学的能力,用科学知识辨别真伪的意识。
活动6:归纳总结与作业1、这节课你学到了什么?2、作业:P171复习题4, 5题. 学生自己总结发言,不足之处由其他学生补充完善,教师重点关注不同层次的学生对知识的理解,掌握程度。 了解教学效果,及时调整教学。
PAGE
1
同课章节目录
