第一章直角三角形的边角关系测试卷(含答案)
文档属性
| 名称 | 第一章直角三角形的边角关系测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024北师版九年级数学下学期单元测试卷
第一章 直角三角形的边角关系
时间:90分钟 满分:100分
题号 一 二 三 评价
错题
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·天津河西区二模)2tan 30°的值等于 ( )
A. B. C. D.
2.(2021·浙江杭州一模)在Rt△ABC中,∠C=90°,AC∶BC=1∶2,则cos A的值为 ( )
A. B.2 C. D.
3.如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A'B'的位置,已知AO的长为4米.若栏杆的旋转角∠AOA'=α,则栏杆A端升高的高度为 ( )
A. 米 B.4sin α米
C. 米 D.4cos α米
4.(2022·河北石家庄模拟)下列说法中正确的是 ( )
A.在Rt△ABC中,若tan A=,则a=4,b=3
B.在Rt△ABC中,∠C=90°,若a=3,b=4,则tan A=
C.tan 30°+tan 60°=1
D.tan A=,则∠A=60°
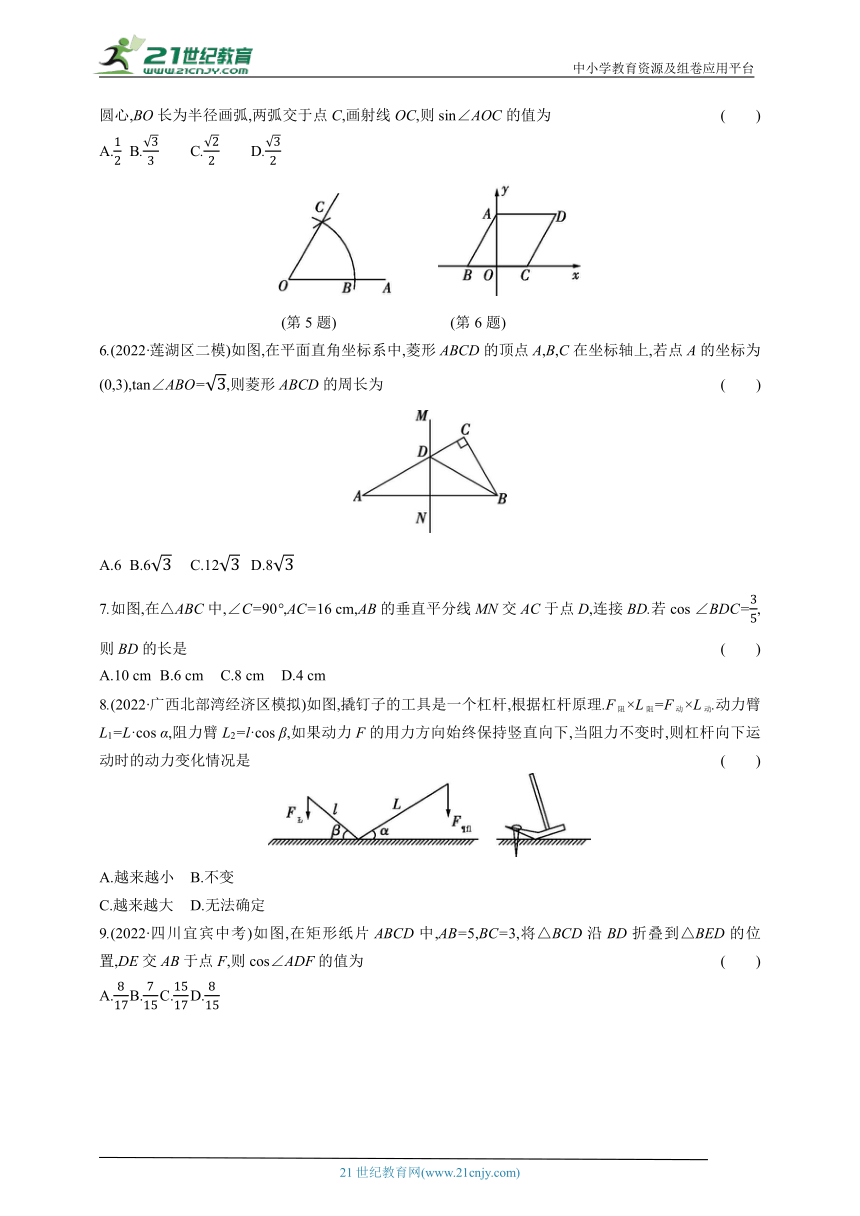
5.(2022·江苏淮安淮阴区模拟)如图,以点O为圆心,任意长为半径画弧,与射线OA交于点B,再以点B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为 ( )
A. B. C. D.
(第5题) (第6题)
6.(2022·莲湖区二模)如图,在平面直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点A的坐标为(0,3),tan∠ABO=,则菱形ABCD的周长为 ( )
A.6 B.6 C.12 D.8
7.如图,在△ABC中,∠C=90°,AC=16 cm,AB的垂直平分线MN交AC于点D,连接BD.若cos ∠BDC=,则BD的长是 ( )
A.10 cm B.6 cm C.8 cm D.4 cm
8.(2022·广西北部湾经济区模拟)如图,撬钉子的工具是一个杠杆,根据杠杆原理.F阻×L阻=F动×L动.动力臂L1=L·cos α,阻力臂L2=l·cos β,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是 ( )
A.越来越小 B.不变
C.越来越大 D.无法确定
9.(2022·四川宜宾中考)如图,在矩形纸片ABCD中,AB=5,BC=3,将△BCD沿BD折叠到△BED的位置,DE交AB于点F,则cos∠ADF的值为 ( )
A. B. C. D.
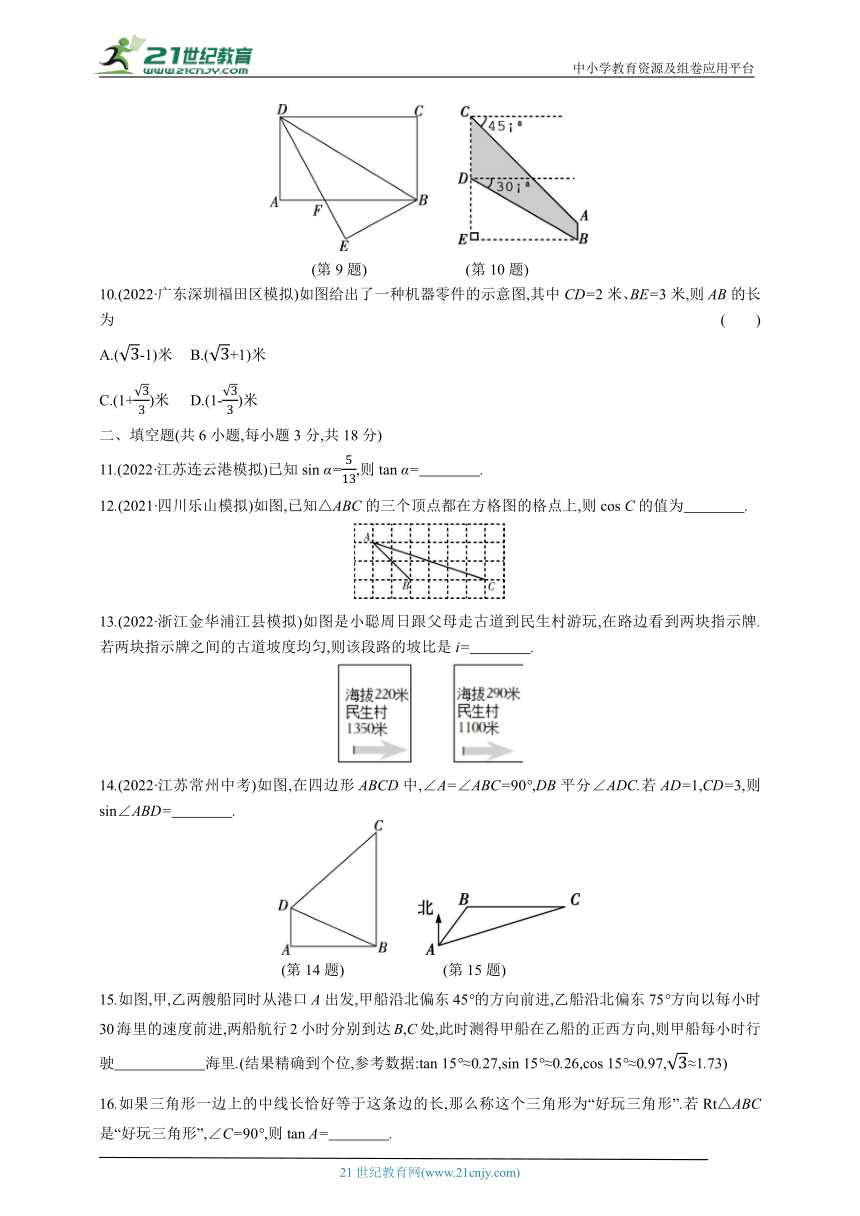
(第9题) (第10题)
10.(2022·广东深圳福田区模拟)如图给出了一种机器零件的示意图,其中CD=2米、BE=3米,则AB的长为 ( )
A.(-1)米 B.(+1)米
C.(1+)米 D.(1-)米
二、填空题(共6小题,每小题3分,共18分)
11.(2022·江苏连云港模拟)已知sin α=,则tan α= .
12.(2021·四川乐山模拟)如图,已知△ABC的三个顶点都在方格图的格点上,则cos C的值为 .
13.(2022·浙江金华浦江县模拟)如图是小聪周日跟父母走古道到民生村游玩,在路边看到两块指示牌.若两块指示牌之间的古道坡度均匀,则该段路的坡比是i= .
14.(2022·江苏常州中考)如图,在四边形ABCD中,∠A=∠ABC=90°,DB平分∠ADC.若AD=1,CD=3,则sin∠ABD= .
(第14题) (第15题)
15.如图,甲,乙两艘船同时从港口A出发,甲船沿北偏东45°的方向前进,乙船沿北偏东75°方向以每小时30海里的速度前进,两船航行2小时分别到达B,C处,此时测得甲船在乙船的正西方向,则甲船每小时行驶 海里.(结果精确到个位,参考数据:tan 15°≈0.27,sin 15°≈0.26,cos 15°≈0.97,≈1.73)
16.如果三角形一边上的中线长恰好等于这条边的长,那么称这个三角形为“好玩三角形”.若Rt△ABC是“好玩三角形”,∠C=90°,则tan A= .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15. 16.
三、解答题(共6小题,共52分)
17.(共2小题,每小题4分,共8分)计算:
(1)(2021·北京石景山区期末)sin 60°·tan 30°+.
(2)(2021·安徽合肥期末)+|1-cos 30°|-2tan 45°·sin 30°.
18.(8分)如图,射线OA放置在3×5的正方形网格中,现请你在图中找出格点(即每个小正方形的顶点)B,并连接OB,AB,使△AOB为直角三角形,且
(1)使tan∠AOB的值为1;
(2)使tan∠AOB的值为.
图(1) 图(2)
19.(8分)小明在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形,已知吊车吊臂的支点O距离地面的高OO'=1.5米,吊臂OA的长度为6米,当吊臂顶端由A点抬升至A'点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊至B'处,并且从O点观测到点A的仰角为45°,点A'的仰角为60°.
(1)求此重物在水平方向移动的距离BC;
(2)求此重物在竖直方向移动的距离B'C.
20.(9分)(2022·江苏泰州海陵区二模)已知△ABC为钝角三角形,其中∠A>90°,有下列条件:
①AB=10;②AC=6;
③tan B=;
④tan C=.
(1)你认为从中至少选择 个条件,可以求出BC边的长;
(2)你选择的条件是 (直接填写序号),并写出求BC的解答过程.
21.(9分)(2022·重庆一中月考)某海域有一小岛P,在以点P为圆心,10(3+)海里为半径R的圆形海域内有暗礁.一海监船自西向东航行,它在A处测得小岛P位于其北偏东60°的方向上,当海监船行驶20海里后到达B处,此时测得小岛P位于B处北偏东45°的方向上.
(1)求A,P之间的距离AP.
(2)若海监船由B处继续向东航行是否有触礁危险 请说明理由.如果有触礁危险,那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域
22.(10分)(2022·山东济宁中考)知识再现
如图(1),在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
∵sin A=,sin B=,
∴c=,c=,
∴=.
拓展探究
如图(2),在锐角三角形ABC中,∠A,∠B,∠C的对边分别为a,b,c.
请探究,,之间的关系,并写出探究过程.
解决问题
如图(3),为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60 m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.
图(1) 图(2) 图(3)
第一章 直角三角形的边角关系
选择填空题答案速查
1 2 3 4 5 6 7 8 9 10
B C B B D D A A C A
11. 12. 13.7∶24
14. 15.11 16.或
1.B 【提示】tan 30°=
2.C 设AC为x,则BC=2x,由勾股定理得AB==x,∴cos A===.故选C.
3.B 如图,过点A'作A'C⊥AB于点C.由题意知A'O=AO=4米,∴sin α=,
∴A'C=4sin α米.故选B.
4.B 在Rt△ABC中,∠C=90°,若tan A=,则a=3x,b=4x,x≠0,故A不正确;在Rt△ABC中,∠C=90°,若a=3,b=4,则tan A=,故B正确;tan 30°+tan 60°=
+=,故C不正确;tan A=,则∠A=30°,故D不正确.故选B.
5.D 如图,连接BC,题意可得OB=OC=BC,则△OBC是等边三角形,故sin∠AOC=sin 60°=.故选D.
6.D ∵点A的坐标为(0,3),∴AO=3.∵tan∠ABO=,∴=,
∴=,∴BO=.∵△AOB是直角三角形,∴AB====2.
∵菱形的四条边相等,∴菱形ABCD的周长为2×4=8.故选D.
7.A ∵cos ∠BDC==,∴设DC=3x cm,BD=5x cm.∵MN是线段AB的垂直平分线,∴AD=BD=5x cm.∵AC=16 cm,∴3x+5x=16,解得x=2,∴BD=10 cm.故选A.
8.A ∵F阻×L阻=F动×L动,∴当阻力及阻力臂不变,动力×动力臂为定值,且定值>0,∴动力随着动力臂的增大而减小.∵杠杆向下运动时的度数越来越小,此时cos α的值越来越大,β的度数越来越大,此时cos β的值越来越小,∴阻力臂越来越小,阻力不变,∴动力×动力臂越来越小,而动力臂越来越大,∴此时动力越来越小.故选A.
9.C ∵四边形ABCD是矩形,∴∠A=90°,AB∥CD,AD=BC=3,CD=AB=5,∴∠BDC=∠DBF.由折叠的性质可得∠BDC=∠BDF,∴∠BDF=∠DBF,∴BF=DF.设BF=x,则DF=x,AF=5-x,在Rt△ADF中,由勾股定理可得AD2+AF2=DF2,即32+(5-x)2=x2,∴x=,
∴cos∠ADF===.故选C.
10.A 如图,延长BA交过C点的水平线于点F.∵∠FCA=45°,BE=3米,∴AF=CF=BE=3米.∵DE=BE·tan 30°=3×=(米),
∴BF=CE=CD+DE=(2+)(米),∴=BF-AF=2+-3=(-1)(米),即AB的长度为(-1)米.故选A.
11. 如图,由于sin α=,所以可设BC=5k,则AB=13k.由勾股定理得AC==12k,∴tan α===.
一题多解 因为sin α=,所以cos α= =,所以tan α==.
高分锦囊 已知α为锐角,则(1)sin2α+cos2α=1;(2)tan α=.
12. 在CB的延长线上取格点D,令∠ADC=90°,如图,在Rt△ADC中,AC===2,∴cos C===.
13.7∶24 由题意得,斜坡的铅直高度为290-220=70(米),坡面距离为1 350-1 100=250(米),则水平距离为=240(米),所以该段路的坡比为70∶240=7∶24.
14. 如图,过点D作DE⊥BC,垂足为E,则四边形ABED是矩形,∴BE=AD=1,DE=AB,∠ADB=∠CBD.∵DB平分∠ADC,∴∠ADB=∠CDB,
∴∠CBD=∠CDB,∴CB=CD=3,∴CE=BC-BE=3-1=2,∴DE===,∴BD===,∴sin∠ABD===.
15.11 设甲船每小时行驶x海里,则AB=2x海里,过点B作BD⊥AC于点D.由题意得,∠BAD=30°,∠C=15°,AC=60海里,∴AD=AB·cos 30°=x≈1.73x(海里),BD=AB·sin 30°=x(海里),DC==≈(海里).
∵AD+DC=AC,∴1.73x+=60,解得x≈11.
一题多解
设甲船每小时行驶x海里,则AB=2x海里,如图,过点B作BD⊥AC于点D,在AC上取点E,使BE=CE,根据题意可知,∠BAD=30°,∠C=15°,∴∠BED=30°,∴DE=AD=AB·cos 30°=x(海里),CE=BE=AB=2x海里,∴AD+DE+CE=60海里,即x+x+2x=60,解得x=15(-1)≈11.
16.或 (分类讨论思想)由题意得,只能是直角边上的中线,故分两种情况讨论.①如图(1),BD是AC边上的中线,BD=AC.设AD=DC=k(k>0),则BD=AC=2k.在Rt△BCD中,∠C=90°,∴BC==k,∴tan A===.②如图(2),AD是BC边上的中线,AD=BC.设BD=DC=m(m>0),则AD=BC=2m.在Rt△ACD中,∠C=90°,
∴AC==m,∴tan∠CAB===.综上所述,tan A的值为或.
图(1) 图(2)
17.【参考答案】(1)原式=×+ (2分)
=+ (3分)
=1. (4分)
(2)原式=-1+1--2×1× (3分)
=-1. (4分)
18.【解题思路】根据tan∠AOB的值分别为1,,构造直角三角形,进而画出△AOB.
【参考答案】(1)如图(1)所示. (4分)
(2)如图(2)所示. (8分)
图(1) 图(2)
19. (1)思路导图
BC
A'EB'C
(2)先解直角三角形A'OE,得出A'E,然后求出B'C.
【参考答案】(1)如图,过点O作OD⊥AB于点D,交A'C于点E.
根据题意可知,EC=DB=OO'=1.5米,ED=BC,∠A=45°,∠A'=30°,∠A'ED=∠ADO=90°. (2分)
在Rt△AOD中,∵cos A=,OA=6米,
∴AD=OD=3 米.
在Rt△A'OE中,∵sin A'=,OA'=6米,
∴OE=3米,
∴BC=ED=OD-OE=(3-3)米,
故此重物在水平方向移动的距离BC是(3-3)米. (5分)
(2)在Rt△A'OE中,A'E=OA'·cos A'=3米.
∴B'C=A'C-A'B'=A'E+CE-AB=A'E+CE-(AD+BD)=3+1.5-(3+1.5)=(3-3)(米),
故此重物在竖直方向移动的距离B'C是(3-3)米.(8分)
20.【参考答案】 (1)3(2分)
(2)①②④ (4分)
过点A作AD⊥BC于点D,如图所示,
设AD=x,
∵tan C=,
∴CD=2x. (6分)
∵AC=6,
根据勾股定理,得x2+(2x)2=(6)2,
解得x=6或x=-6(不合题意,舍去),
∴AD=6,CD=2x=12.
∵AB=10,
根据勾股定理,得BD==8,
∴BC=CD+BD=12+8=20. (9分)
(本题答案不唯一,也可选择①②③)
一题多解
(2)①②④ (4分)
解答过程如下.
如图,过点B作BE⊥CA,交CA的延长线于点E.
在Rt△BCE中,tan C==,
∴设BE=x,则CE=2x,
∴AE=2x-6.
在Rt△BAE中,由勾股定理得,AE2+BE2=AB2,
即(2x-6)2+x2=102,
解得x=4或x=(不合题意,舍去),
∴BE=4,CE=8,
∴在Rt△BCE中,BC===20.(9分)
(本大题答案不唯一,也可选择①②③)
21.【参考答案】(1)如图,过点P作PC⊥AB,交AB的延长线于点C,
由题意得,∠PAC=30°,∠PBC=45°,AB=20.
设PC=x,则BC=x.
在Rt△PAC中,
∵tan 30°===,
∴x=10+10,
∴PA=2x=20+20.
答:A,P之间的距离AP为(20+20)海里. (4分)
(2)∵PC-10(3+)=10+10-30-10=10(-3+-)<0,
∴有触礁的危险. (6分)
设海监船无触礁危险的新航线为射线BD,作PE⊥BD,垂足为点E,
当P到BD的距离PE=10(3+)海里时,
有sin∠PBE===, (8分)
∴∠PBD=60°,
∴∠CBD=60°-45°=15°.
90°-15°=75°,
即海监船由B处开始沿南偏东至多75°的方向航行能安全通过这一海域. (9分)
高分锦囊
解直角三角形实际应用题的一般步骤
(1)审题:根据题意画出图形,建立数学模型.
(2)构造直角三角形:将已知条件转化到示意图中,把实际问题转化为解直角三角形问题.
(3)列关系式:选择合适的边角关系式,使运算简便、准确.
(4)检验:得出数学问题的答案并检验答案是否符合实际意义,同时还要注意结果有无对精确度的要求.
22.【参考答案】拓展探究
如图,作CD⊥AB于点D,AE⊥BC于点E,
在Rt△ABE中,sin B==,
同理得,sin B==,
sin∠BAC==,
sin∠BCA==,
∴AE=csin B,AE=bsin∠BCA,CD=asin B,CD=bsin∠BAC,
∴=,=,
∴==. (6分)
解决问题 在△ABC中,∠B=180°-∠A-∠C=45°.
由拓展探究中的结论,得=,即=,
∴AB===30(m).
答:点A到点B的距离为30 m.(10分)
一题多解
拓展探究 如图,作△ABC的外接圆☉O,连接BO并延长,交☉O于点D,连接CD,则∠A=∠D.
设☉O的直径为2r.
∵BD是☉O的直径,∴∠BCD=90°.
在Rt△BCD中,sin D=,
∴BD=,即2r=.
同理可得,=2r,=2r,
故==. (6分)
高分锦囊
类比探究型问题的解题通法
类比探究型问题是共性条件与特殊条件相结合、由特殊情形到一般情形(或由简单情形到复杂情形)逐步深入、解题思路一脉相承的综合性题目.解决类比探究型问题的一般方法:
(1)根据题干,结合分支条件解决第一问;
(2)用解决上一问的方法类比解决下一问,如果不能,两问结合起来分析,找出不能类比的原因和不变特征,依据不变特征,探索新的解题方法(照搬字母,照搬辅助线,照搬全等或相似,也就是知识的迁移).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师版九年级数学下学期单元测试卷
第一章 直角三角形的边角关系
时间:90分钟 满分:100分
题号 一 二 三 评价
错题
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·天津河西区二模)2tan 30°的值等于 ( )
A. B. C. D.
2.(2021·浙江杭州一模)在Rt△ABC中,∠C=90°,AC∶BC=1∶2,则cos A的值为 ( )
A. B.2 C. D.
3.如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A'B'的位置,已知AO的长为4米.若栏杆的旋转角∠AOA'=α,则栏杆A端升高的高度为 ( )
A. 米 B.4sin α米
C. 米 D.4cos α米
4.(2022·河北石家庄模拟)下列说法中正确的是 ( )
A.在Rt△ABC中,若tan A=,则a=4,b=3
B.在Rt△ABC中,∠C=90°,若a=3,b=4,则tan A=
C.tan 30°+tan 60°=1
D.tan A=,则∠A=60°
5.(2022·江苏淮安淮阴区模拟)如图,以点O为圆心,任意长为半径画弧,与射线OA交于点B,再以点B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为 ( )
A. B. C. D.
(第5题) (第6题)
6.(2022·莲湖区二模)如图,在平面直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点A的坐标为(0,3),tan∠ABO=,则菱形ABCD的周长为 ( )
A.6 B.6 C.12 D.8
7.如图,在△ABC中,∠C=90°,AC=16 cm,AB的垂直平分线MN交AC于点D,连接BD.若cos ∠BDC=,则BD的长是 ( )
A.10 cm B.6 cm C.8 cm D.4 cm
8.(2022·广西北部湾经济区模拟)如图,撬钉子的工具是一个杠杆,根据杠杆原理.F阻×L阻=F动×L动.动力臂L1=L·cos α,阻力臂L2=l·cos β,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是 ( )
A.越来越小 B.不变
C.越来越大 D.无法确定
9.(2022·四川宜宾中考)如图,在矩形纸片ABCD中,AB=5,BC=3,将△BCD沿BD折叠到△BED的位置,DE交AB于点F,则cos∠ADF的值为 ( )
A. B. C. D.
(第9题) (第10题)
10.(2022·广东深圳福田区模拟)如图给出了一种机器零件的示意图,其中CD=2米、BE=3米,则AB的长为 ( )
A.(-1)米 B.(+1)米
C.(1+)米 D.(1-)米
二、填空题(共6小题,每小题3分,共18分)
11.(2022·江苏连云港模拟)已知sin α=,则tan α= .
12.(2021·四川乐山模拟)如图,已知△ABC的三个顶点都在方格图的格点上,则cos C的值为 .
13.(2022·浙江金华浦江县模拟)如图是小聪周日跟父母走古道到民生村游玩,在路边看到两块指示牌.若两块指示牌之间的古道坡度均匀,则该段路的坡比是i= .
14.(2022·江苏常州中考)如图,在四边形ABCD中,∠A=∠ABC=90°,DB平分∠ADC.若AD=1,CD=3,则sin∠ABD= .
(第14题) (第15题)
15.如图,甲,乙两艘船同时从港口A出发,甲船沿北偏东45°的方向前进,乙船沿北偏东75°方向以每小时30海里的速度前进,两船航行2小时分别到达B,C处,此时测得甲船在乙船的正西方向,则甲船每小时行驶 海里.(结果精确到个位,参考数据:tan 15°≈0.27,sin 15°≈0.26,cos 15°≈0.97,≈1.73)
16.如果三角形一边上的中线长恰好等于这条边的长,那么称这个三角形为“好玩三角形”.若Rt△ABC是“好玩三角形”,∠C=90°,则tan A= .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15. 16.
三、解答题(共6小题,共52分)
17.(共2小题,每小题4分,共8分)计算:
(1)(2021·北京石景山区期末)sin 60°·tan 30°+.
(2)(2021·安徽合肥期末)+|1-cos 30°|-2tan 45°·sin 30°.
18.(8分)如图,射线OA放置在3×5的正方形网格中,现请你在图中找出格点(即每个小正方形的顶点)B,并连接OB,AB,使△AOB为直角三角形,且
(1)使tan∠AOB的值为1;
(2)使tan∠AOB的值为.
图(1) 图(2)
19.(8分)小明在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形,已知吊车吊臂的支点O距离地面的高OO'=1.5米,吊臂OA的长度为6米,当吊臂顶端由A点抬升至A'点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊至B'处,并且从O点观测到点A的仰角为45°,点A'的仰角为60°.
(1)求此重物在水平方向移动的距离BC;
(2)求此重物在竖直方向移动的距离B'C.
20.(9分)(2022·江苏泰州海陵区二模)已知△ABC为钝角三角形,其中∠A>90°,有下列条件:
①AB=10;②AC=6;
③tan B=;
④tan C=.
(1)你认为从中至少选择 个条件,可以求出BC边的长;
(2)你选择的条件是 (直接填写序号),并写出求BC的解答过程.
21.(9分)(2022·重庆一中月考)某海域有一小岛P,在以点P为圆心,10(3+)海里为半径R的圆形海域内有暗礁.一海监船自西向东航行,它在A处测得小岛P位于其北偏东60°的方向上,当海监船行驶20海里后到达B处,此时测得小岛P位于B处北偏东45°的方向上.
(1)求A,P之间的距离AP.
(2)若海监船由B处继续向东航行是否有触礁危险 请说明理由.如果有触礁危险,那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域
22.(10分)(2022·山东济宁中考)知识再现
如图(1),在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
∵sin A=,sin B=,
∴c=,c=,
∴=.
拓展探究
如图(2),在锐角三角形ABC中,∠A,∠B,∠C的对边分别为a,b,c.
请探究,,之间的关系,并写出探究过程.
解决问题
如图(3),为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60 m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.
图(1) 图(2) 图(3)
第一章 直角三角形的边角关系
选择填空题答案速查
1 2 3 4 5 6 7 8 9 10
B C B B D D A A C A
11. 12. 13.7∶24
14. 15.11 16.或
1.B 【提示】tan 30°=
2.C 设AC为x,则BC=2x,由勾股定理得AB==x,∴cos A===.故选C.
3.B 如图,过点A'作A'C⊥AB于点C.由题意知A'O=AO=4米,∴sin α=,
∴A'C=4sin α米.故选B.
4.B 在Rt△ABC中,∠C=90°,若tan A=,则a=3x,b=4x,x≠0,故A不正确;在Rt△ABC中,∠C=90°,若a=3,b=4,则tan A=,故B正确;tan 30°+tan 60°=
+=,故C不正确;tan A=,则∠A=30°,故D不正确.故选B.
5.D 如图,连接BC,题意可得OB=OC=BC,则△OBC是等边三角形,故sin∠AOC=sin 60°=.故选D.
6.D ∵点A的坐标为(0,3),∴AO=3.∵tan∠ABO=,∴=,
∴=,∴BO=.∵△AOB是直角三角形,∴AB====2.
∵菱形的四条边相等,∴菱形ABCD的周长为2×4=8.故选D.
7.A ∵cos ∠BDC==,∴设DC=3x cm,BD=5x cm.∵MN是线段AB的垂直平分线,∴AD=BD=5x cm.∵AC=16 cm,∴3x+5x=16,解得x=2,∴BD=10 cm.故选A.
8.A ∵F阻×L阻=F动×L动,∴当阻力及阻力臂不变,动力×动力臂为定值,且定值>0,∴动力随着动力臂的增大而减小.∵杠杆向下运动时的度数越来越小,此时cos α的值越来越大,β的度数越来越大,此时cos β的值越来越小,∴阻力臂越来越小,阻力不变,∴动力×动力臂越来越小,而动力臂越来越大,∴此时动力越来越小.故选A.
9.C ∵四边形ABCD是矩形,∴∠A=90°,AB∥CD,AD=BC=3,CD=AB=5,∴∠BDC=∠DBF.由折叠的性质可得∠BDC=∠BDF,∴∠BDF=∠DBF,∴BF=DF.设BF=x,则DF=x,AF=5-x,在Rt△ADF中,由勾股定理可得AD2+AF2=DF2,即32+(5-x)2=x2,∴x=,
∴cos∠ADF===.故选C.
10.A 如图,延长BA交过C点的水平线于点F.∵∠FCA=45°,BE=3米,∴AF=CF=BE=3米.∵DE=BE·tan 30°=3×=(米),
∴BF=CE=CD+DE=(2+)(米),∴=BF-AF=2+-3=(-1)(米),即AB的长度为(-1)米.故选A.
11. 如图,由于sin α=,所以可设BC=5k,则AB=13k.由勾股定理得AC==12k,∴tan α===.
一题多解 因为sin α=,所以cos α= =,所以tan α==.
高分锦囊 已知α为锐角,则(1)sin2α+cos2α=1;(2)tan α=.
12. 在CB的延长线上取格点D,令∠ADC=90°,如图,在Rt△ADC中,AC===2,∴cos C===.
13.7∶24 由题意得,斜坡的铅直高度为290-220=70(米),坡面距离为1 350-1 100=250(米),则水平距离为=240(米),所以该段路的坡比为70∶240=7∶24.
14. 如图,过点D作DE⊥BC,垂足为E,则四边形ABED是矩形,∴BE=AD=1,DE=AB,∠ADB=∠CBD.∵DB平分∠ADC,∴∠ADB=∠CDB,
∴∠CBD=∠CDB,∴CB=CD=3,∴CE=BC-BE=3-1=2,∴DE===,∴BD===,∴sin∠ABD===.
15.11 设甲船每小时行驶x海里,则AB=2x海里,过点B作BD⊥AC于点D.由题意得,∠BAD=30°,∠C=15°,AC=60海里,∴AD=AB·cos 30°=x≈1.73x(海里),BD=AB·sin 30°=x(海里),DC==≈(海里).
∵AD+DC=AC,∴1.73x+=60,解得x≈11.
一题多解
设甲船每小时行驶x海里,则AB=2x海里,如图,过点B作BD⊥AC于点D,在AC上取点E,使BE=CE,根据题意可知,∠BAD=30°,∠C=15°,∴∠BED=30°,∴DE=AD=AB·cos 30°=x(海里),CE=BE=AB=2x海里,∴AD+DE+CE=60海里,即x+x+2x=60,解得x=15(-1)≈11.
16.或 (分类讨论思想)由题意得,只能是直角边上的中线,故分两种情况讨论.①如图(1),BD是AC边上的中线,BD=AC.设AD=DC=k(k>0),则BD=AC=2k.在Rt△BCD中,∠C=90°,∴BC==k,∴tan A===.②如图(2),AD是BC边上的中线,AD=BC.设BD=DC=m(m>0),则AD=BC=2m.在Rt△ACD中,∠C=90°,
∴AC==m,∴tan∠CAB===.综上所述,tan A的值为或.
图(1) 图(2)
17.【参考答案】(1)原式=×+ (2分)
=+ (3分)
=1. (4分)
(2)原式=-1+1--2×1× (3分)
=-1. (4分)
18.【解题思路】根据tan∠AOB的值分别为1,,构造直角三角形,进而画出△AOB.
【参考答案】(1)如图(1)所示. (4分)
(2)如图(2)所示. (8分)
图(1) 图(2)
19. (1)思路导图
BC
A'EB'C
(2)先解直角三角形A'OE,得出A'E,然后求出B'C.
【参考答案】(1)如图,过点O作OD⊥AB于点D,交A'C于点E.
根据题意可知,EC=DB=OO'=1.5米,ED=BC,∠A=45°,∠A'=30°,∠A'ED=∠ADO=90°. (2分)
在Rt△AOD中,∵cos A=,OA=6米,
∴AD=OD=3 米.
在Rt△A'OE中,∵sin A'=,OA'=6米,
∴OE=3米,
∴BC=ED=OD-OE=(3-3)米,
故此重物在水平方向移动的距离BC是(3-3)米. (5分)
(2)在Rt△A'OE中,A'E=OA'·cos A'=3米.
∴B'C=A'C-A'B'=A'E+CE-AB=A'E+CE-(AD+BD)=3+1.5-(3+1.5)=(3-3)(米),
故此重物在竖直方向移动的距离B'C是(3-3)米.(8分)
20.【参考答案】 (1)3(2分)
(2)①②④ (4分)
过点A作AD⊥BC于点D,如图所示,
设AD=x,
∵tan C=,
∴CD=2x. (6分)
∵AC=6,
根据勾股定理,得x2+(2x)2=(6)2,
解得x=6或x=-6(不合题意,舍去),
∴AD=6,CD=2x=12.
∵AB=10,
根据勾股定理,得BD==8,
∴BC=CD+BD=12+8=20. (9分)
(本题答案不唯一,也可选择①②③)
一题多解
(2)①②④ (4分)
解答过程如下.
如图,过点B作BE⊥CA,交CA的延长线于点E.
在Rt△BCE中,tan C==,
∴设BE=x,则CE=2x,
∴AE=2x-6.
在Rt△BAE中,由勾股定理得,AE2+BE2=AB2,
即(2x-6)2+x2=102,
解得x=4或x=(不合题意,舍去),
∴BE=4,CE=8,
∴在Rt△BCE中,BC===20.(9分)
(本大题答案不唯一,也可选择①②③)
21.【参考答案】(1)如图,过点P作PC⊥AB,交AB的延长线于点C,
由题意得,∠PAC=30°,∠PBC=45°,AB=20.
设PC=x,则BC=x.
在Rt△PAC中,
∵tan 30°===,
∴x=10+10,
∴PA=2x=20+20.
答:A,P之间的距离AP为(20+20)海里. (4分)
(2)∵PC-10(3+)=10+10-30-10=10(-3+-)<0,
∴有触礁的危险. (6分)
设海监船无触礁危险的新航线为射线BD,作PE⊥BD,垂足为点E,
当P到BD的距离PE=10(3+)海里时,
有sin∠PBE===, (8分)
∴∠PBD=60°,
∴∠CBD=60°-45°=15°.
90°-15°=75°,
即海监船由B处开始沿南偏东至多75°的方向航行能安全通过这一海域. (9分)
高分锦囊
解直角三角形实际应用题的一般步骤
(1)审题:根据题意画出图形,建立数学模型.
(2)构造直角三角形:将已知条件转化到示意图中,把实际问题转化为解直角三角形问题.
(3)列关系式:选择合适的边角关系式,使运算简便、准确.
(4)检验:得出数学问题的答案并检验答案是否符合实际意义,同时还要注意结果有无对精确度的要求.
22.【参考答案】拓展探究
如图,作CD⊥AB于点D,AE⊥BC于点E,
在Rt△ABE中,sin B==,
同理得,sin B==,
sin∠BAC==,
sin∠BCA==,
∴AE=csin B,AE=bsin∠BCA,CD=asin B,CD=bsin∠BAC,
∴=,=,
∴==. (6分)
解决问题 在△ABC中,∠B=180°-∠A-∠C=45°.
由拓展探究中的结论,得=,即=,
∴AB===30(m).
答:点A到点B的距离为30 m.(10分)
一题多解
拓展探究 如图,作△ABC的外接圆☉O,连接BO并延长,交☉O于点D,连接CD,则∠A=∠D.
设☉O的直径为2r.
∵BD是☉O的直径,∴∠BCD=90°.
在Rt△BCD中,sin D=,
∴BD=,即2r=.
同理可得,=2r,=2r,
故==. (6分)
高分锦囊
类比探究型问题的解题通法
类比探究型问题是共性条件与特殊条件相结合、由特殊情形到一般情形(或由简单情形到复杂情形)逐步深入、解题思路一脉相承的综合性题目.解决类比探究型问题的一般方法:
(1)根据题干,结合分支条件解决第一问;
(2)用解决上一问的方法类比解决下一问,如果不能,两问结合起来分析,找出不能类比的原因和不变特征,依据不变特征,探索新的解题方法(照搬字母,照搬辅助线,照搬全等或相似,也就是知识的迁移).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
