第二章二次函数测试卷（含答案）

中小学教育资源及组卷应用平台
2024北师版九年级数学下学期单元测试卷
第二章　二次函数
时间:90分钟　 满分:100分
题号 一 二 三 评价
错题
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
　　　　　　 　　　　　　　　　　
1.(2022·山西二模)用配方法将二次函数y=x2-2x-4化为y=a(x-h)2+k的形式为(　　)
A.y=(x-2)2-4 B.y=(x-1)2-3
C.y=(x-1)2-5 D.y=(x-2)2-6
2.(2022·广东深圳龙岗区期末)长方形的周长为12 cm,其中一边为x(0A.y=(12-x)2　　 B.y=(6-x)2
C.y=-x2+12x　　　 D.y=-x2+6x
3.如图,直线y1=mx+n与抛物线y2=ax2+bx+c交于A(-3,1)和B(1,2)两点,则使y1>y2的x的取值范围是 (　　)
A.x>1
B.x>-3
C.x>1或x<-3
D.-34.(2022·江苏泰安中考改编)抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x -2 -1 0 1
y 0 4 6 6
下列结论不正确的是 (　　)
A.抛物线的开口向下
B.抛物线的对称轴为直线x=
C.抛物线与x轴的一个交点坐标为(2,0)
D.一定经过点(3,0)
5.(2022·湖南株洲期末)已知二次函数y=ax2+bx-c(a≠0),其中b>0,c>0,则该函数的图象可能为 (　　)
A B C D
6.(2021·广东广州番禺区校级期中)若二次函数y=x2-6x+5,当2≤x≤6时的最大值是n,最小值是m,则n-m= (　　)
A.3 B.9 C.7 D.5
7.(2022·广西桂林模拟)小林说:将二次函数y=x2的图象平移或翻折后经过点(2,0)有如下4种方法.
①向右平移2个单位长度;②向右平移1个单位长度,再向下平移1个单位长度;③向下平移4个单位长度;④沿x轴翻折,再向上平移4个单位长度;你认为小林说的方法中正确的个数有 (　　)
A.1个　 B.2个　 C.3个　 D.4个
8.(2022·江苏常熟模拟)在平面直角坐标系中,若点P的横坐标与纵坐标的和为零,则称点P为“零和点”.已知二次函数y=x2+3x+m的图象上有且只有一个“零和点”,则下列结论正确的是 (　　)
A.m=　 B.m=　 C.m=1　 D.m=4
9.(2022·河北石家庄三模)某池塘的截面如图所示,池底呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:m).有下列结论:
①AB=24 m;②池底所在抛物线的表达式为y=x2-5;③池塘最深处到水面CD的距离为1.8 m;④若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离减少为原来的.其中结论正确的是 (　　)
A.①②　 B.②④　 C.③④　 D.①④
10.如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,动点P在线段DE上(不与D,E重合),过点P作PQ∥BD交BE于点Q,连接QD.设PD=x,△PQD的面积为y,则能表示y与x之间的函数关系的图象大致是 (　　)
A　　 B C　　 D
二、填空题(共6小题,每小题3分,共18分)
11.(2021·安徽合肥期末)若y=(2-a)是二次函数,则a=　　　　.
12.已知抛物线y=x2-x-1与x轴的一个交点为(m,0),则代数式-2m2+2m+2 023的值为　　　　.
13.(2022·吉林长春宽城区模拟)在平面直角坐标系中,直线y=m-1与函数y=x2-2x-1(x≥0)的图象有两个公共点.若m为无理数,则m的值可以为 　　　　.(写出一个即可)
14.(2022·安徽合肥五十中西校月考)某种型号的小型无人机着陆后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数表达式是s=10t-0.25t2,则无人机着陆后滑行　　　秒才能停下来.
15.(2022·江苏南京树人中学二模)小淇利用绘图软件画出函数y=-x(x-1)(x+1)(-2≤x≤2)的图象,下列关于该函数性质的四种说法:
①图象与x轴有两个交点;
②图象关于原点中心对称;
③最大值是3,最小值是-3;
④当x>1时,y随x的增大而减小.
其中,所有正确说法的序号是　　　　.
16.已知y关于x的函数y=k2x2-(2k-1)x+1的图象与坐标轴只有两个不同的交点A,B,P点坐标为(3,2),则△PAB的面积为　　　　　　.
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11.　　　 12.　　　 13.　　　
14.　　　 15.　　　 16.　　　
三、解答题(共6小题,共52分)
17. (6分)(2022·山东淄博期末)已知二次函数y=ax2+bx+3的图象经过点(-3,0),(2,-5).
(1)求二次函数的表达式;
(2)请你判断点P(-2,3)是否在这个二次函数的图象上.
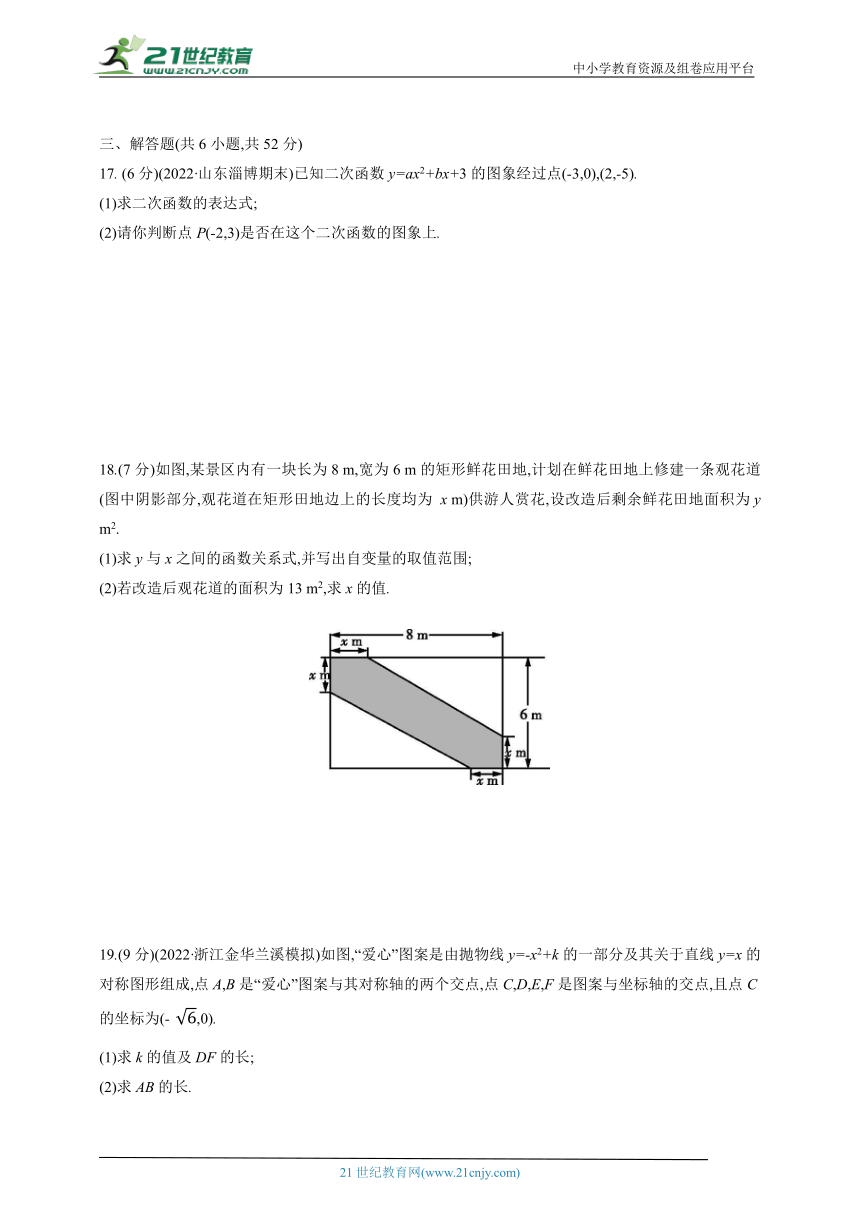
18.(7分)如图,某景区内有一块长为8 m,宽为6 m的矩形鲜花田地,计划在鲜花田地上修建一条观花道(图中阴影部分,观花道在矩形田地边上的长度均为 x m)供游人赏花,设改造后剩余鲜花田地面积为y m2.
(1)求y与x之间的函数关系式,并写出自变量的取值范围;
(2)若改造后观花道的面积为13 m2,求x的值.
19.(9分)(2022·浙江金华兰溪模拟)如图,“爱心”图案是由抛物线y=-x2+k的一部分及其关于直线y=x的对称图形组成,点A,B是“爱心”图案与其对称轴的两个交点,点C,D,E,F是图案与坐标轴的交点,且点C的坐标为(-,0).
(1)求k的值及DF的长;
(2)求AB的长.
20.(10分)(2022·山东潍坊中考节选)为落实“双减”,老师布置了一项这样的课后作业:
二次函数的图象经过点(-1,-1),且不经过第一象限,写出满足这些条件的一个函数表达式.
【观察发现】
请完成作业,并在直角坐标系中画出大致图象.
【思考交流】
小亮说:“满足条件的函数图象的对称轴一定在y轴的左侧.”
小莹说:“满足条件的函数图象一定在x轴的下方.”
你认同他们的说法吗 若不认同,请举例说明.
21.(10分)(2022·江西中考改编)跳台滑雪运动可分为助滑、起跳、飞行和落地四个阶段,运动员起跳后飞行的路线是抛物线的一部分(如图中实线部分所示),落地点在着陆坡(如图中虚线部分所示)上,着陆坡上的基准点K为飞行距离计分的参照点,落地点超过K点越远,飞行距离分越高.2022年北京冬奥会跳台滑雪标准台的起跳台的高度OA为66 m,基准点K到起跳台的水平距离为75 m,高度为h m(h为定值).设运动员从起跳点A起跳后的高度y(m)与水平距离x(m)之间的函数关系为y=ax2+bx+c(a≠0).
(1)c的值为　　　　.
(2)①若运动员落地点恰好到达K点,且此时a=-,b=,求基准点K的高度h;
②若a=-时,运动员落地点要超过K点,则b的取值范围为　　　　.
22.(10分)(2022·陕西榆林榆阳区一模改编)如图,若抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,直线y=x-3经过点B,C.
(1)求二次函数的表达式.
(2)点P是直线BC下方抛物线上一动点,过点P作PH⊥x轴于点H,交BC于点M,连接PC.
①线段PM是否有最大值 如果有,求出最大值;如果没有,请说明理由.
②在点P运动的过程中,是否存在点M,恰好使△PCM是以PM为腰的等腰三角形 如果存在,请求出点P的坐标;如果不存在,请说明理由.
第二章　二次函数
选择填空题答案速查
1 2 3 4 5 6 7 8 9 10
C D D C C B D D B C
11.-2 12.2 021 13.-+1(答案不唯一)
14.20 15.②③④ 16.1或
1.C
2.D　∵长方形的周长为12 cm,其中一边长为x cm,∴另一边长为(6-x)cm,面积y=x(6-x)=-x2+6x.故选D.
3.D　∵直线y1=mx+n与抛物线y2=ax2+bx+c交于A(-3,1)和B (1,2)两点,∴由图象可知,直线y1=mx+n在抛物线y2=ax2+bx+c上方时,y1>y2,此时自变量x的取值范围为-3破题关键
解答此题的关键是利用数形结合的思想方法找出当y1>y2时,自变量x的取值范围.
4.C　由表格可得,解得∴y=-x2+x+6,∴该抛物线的开口向下,故选项A正确,不符合题意;该抛物线的对称轴是直线x=-=,故选项B正确,不符合题意;∵当x=-2时,y=0,∴当x=×2-(-2)=3时,y=0,故选项C错误,选项D正确,即C选项符合题意.故选C.
5.C　∵c>0,∴-c<0,故A,D选项不正确;当a>0时,∵b>0,∴对称轴x=-<0,故B选项不正确;当a<0时,b>0,∴对称轴x=->0,故C选项正确.故选C.
快捷妙解
∵b>0,c>0,∴可令b=2,c=1,则函数为y=ax2+2x-1,由此可知抛物线与y轴交于(0,-1),故排除选项A,D.令a=1,则对称轴为x=-1,选项B不成立,故正确答案为C.
6.B
图示速解
y=x2-6x+5可化为y=(x-3)2-4,可知二次函数的顶点坐标为(3,-4),所以最小值m=-4.当x=6时,y=(6-3)2-4=5,即n=5.则n-m=5-(-4)=9.
7.D　①向右平移2个单位长度,则平移后的表达式为y=(x-2)2,当x=2时,y=0,所以平移后的抛物线过点(2,0),故①符合题意;②向右平移1个单位长度,再向下平移1个单位长度,则平移后的表达式为y=(x-1)2-1,当x=2时,y=0,所以平移后的抛物线过点(2,0),故②符合题意;③向下平移4个单位长度,则平移后的表达式为y=x2-4,当x=2时,y=0,所以平移后的抛物线过点(2,0),故③符合题意;④沿x轴翻折,再向上平移4个单位长度,则平移后的表达式为y=-x2+4,当x=2时,y=0,所以平移后的抛物线过点(2,0),故④符合题意.故选D.
高分锦囊
抛物线的平移规律
(1)将抛物线的表达式转化为顶点式y= a(x-h)2+k,确定其顶点坐标.
(2)在原有函数的基础上,向右平移m个单位,则平移后的表达式为y=a(x-h-m)2+k,向左平移m个单位,则平移后的表达式为y=a(x-h+m)2+k;向上平移 n个单位,则平移后的表达式为y=a(x-h)2+k+n;向下平移 n个单位,则平移后的表达式为y=a(x-h)2+k-n.
8.D　由题意得点P在直线y=-x上,∴y=x2+3x+m的图象上有且只有一个“零和点”时,方程x2+3x+m=-x有两个相同的解,∴Δ=b2-4ac=42-4m=0,解得m=4.故选D.
9.B　观察图形可知AB=30 m,故①错误;设池底所在抛物线的表达式为y=ax2-5,将(15,0)代入,可得a=,故拋物线的表达式为y=x2-5,故②正确;∵y=x2-5,∴当x=12时,y=-1.8,故池塘最深处到水面CD的距离为5-1.8=3.2(m),故③错误;当池塘中水面的宽度减少为原来的一半,即水面宽度为12 m时,将x=6代入y=x2-5,得y=-4.2,可知此时最深处到水面的距离为5-4.2=0.8(m),即为原来的,故④正确.故选B.
10.C　过点Q作QF⊥AD于点F.在Rt△ABE中,∵∠ABE=45°，∴BE=AB=
2,∴DE=BE=2.∵PQ∥BD,∴∠EPQ=∠EDB,∠EQP=∠EBD.∵BE=DE,
∴∠EDB=∠EBD,∴∠EPQ=∠EQP,∴QE=PE=2-x.在Rt△EQF中,∠FEQ=45°,
∴QF=EQ=2-x,∴y=x(2-x)=-x2+x(011.-2　由题意得a2-2=2且2-a≠0,解得a=-2.
12.2 021　将(m,0)代入y=x2-x-1,得m2-m-1=0,所以m2-m=1,则-2m2+2m+2 023=-2(m2-m)+2 023=-2+2 023=2 021.
13.-+1(答案不唯一,或-+1等)　∵y=x2-2x-1=(x-1)2-2,∴抛物线开口向上,顶点坐标为(1,-2),将x=0代入y=x2-2x-1得y=-1,∴当-214.20　s=10t-0.25t2=-0.25(t-20)2+100,即当无人机着陆后滑行20秒,无人机才能停下来.
15.②③④　①图象与x轴有三个交点,故①错误;②图象关于原点中心对称,故②正确;③当x=-2时,y=3,当x=2时,y=-3,∴函数的最大值是3,最小值是-3,故③正确;④当x>1时,y随x的增大而减小,故④正确.
16.1或　设点A,B分别是函数的图象与x轴,y轴的交点.①当k≠0时,该函数为二次函数,函数与坐标轴只有两个不同的交点,则Δ=(1-2k)2-4k2=0,解得k=,所以y=x2+x+1,令y=0,则x=-4,令x=0,则y=1,故A(-4,0),B(0,1).如图,设直线AP交y轴于点H,直线AP的函数表达式为y=ax+b,则解得故直线AP的函数表达式为y=x+.令x=0,则y=,故H(0,),所以BH=-1=,所以S△PAB=S△BHA+S△BHP=××(xP-xA)=××(3+4)=.②当k=0时,y=x+1,直线和坐标轴只有两个交点,即点A(-1,0),B(0,1).同理可得直线AP的函数表达式为y=x+,故H(0,)(点H在点B下方),所以BH=1-=,所以S△PAB=S△BHA+S△BHP=××(xP-xA)=××(3+1)=1.综上所述,△PAB的面积为1或.
排雷避坑
本题易出现的错误是只考虑二次函数的情况,而忽视函数有可能是一次函数.
17.【参考答案】(1)把(-3,0),(2,-5)代入y=ax2+bx+3,
得
解得
则二次函数的表达式为y=-x2-2x+3. (4分)
(2)当x=-2时,y=-(-2)2-2×(-2)+3=3,
即点P(-2,3)在这个二次函数的图象上.　 (6分)
18.【参考答案】(1)由题意得,y=(8-x)(6-x)×2=x2-14x+48(0(2)由题意,得6×8-(x2-14x+48)=13,
解得x1=1,x2=13(舍去),
所以x=1,
故当观花道的面积为13 m2时,x的值是1. (7分)
19.【参考答案】 (1)把C(-,0)的坐标代入y=-x2+k,得 0=-6+k,
∴k=6,
∴抛物线的解析式为y=-x2+6,
∴D(0,6),
∴OD=6.
∵C(-,0),
∴OC=,
由对称性质知,OF=OC=,
∴DF=OD+OF=6+. (4分)
(2)∵“爱心”图案是由抛物线y=-x2+k的一部分及其关于直线y=x的对称图形组成,
∴联立
解得或
∴A(2,2),B(-3,-3). (6分)
如图,过点A作关于y轴平行的直线,过点B作关于x轴平行的直线,两直线交于点P,
由图可知,AP=yA-yB=5,BP=xA-xB=5,
∴AB==5. (9分)
20.【参考答案】y=-x2(答案不为唯一). (3分)
【观察发现】如图所示:
(6分)
【思考交流】∵抛物线的对称轴为x=-,a<0,
∴抛物线的对称轴可以在y轴的左侧,
也可以在y轴的右侧,或者是y轴,例如:y=-x2,
∴小亮的说法不正确.
∵抛物线不经过第一象限,
∴抛物线的图象不一定在x轴的下方,
∴小莹的说法不正确. (10分)
21.【参考答案】 (1)66 (2分)
(2)①∵a=-,b=,c=66,
∴y=-x2+x+66.
当x=75时,y=-×752+×75+66=21,
∴h的值为21. (6分)
②b> (10分)
解法提示:
方法一:∵a=-,c=66,
∴y=-x2+bx+66.
将x=75代入,得y=75b-.
运动员落地点要超过K点,则y=75b->21,
解得b>.
方法二:抛物线y=-x2+bx+66与①中抛物线y=-x2+x+66开口方向及开口大小都相同,且与y轴交于同一个点,所以只要满足对称轴在抛物线y=-x2+x+66的对称轴的右侧,落地点就能超过K点.
由->-,得b>.
22.【解题思路】(1)先求出B,C两点的坐标,然后代入y=x2+bx+c中求b,c的值,即可求出二次函数的表达式.(2)①列出PM关于x的二次函数表达式,并求出函数的最大值;②分PM=PC,PM=MC两种情况求解.
【参考答案】(1)∵直线y=x-3经过点B,C,当x=0时,y=-3,当y=0时,x=3,
∴B(3,0),C(0,-3).
将B,C两点的坐标代入y=x2+bx+c,
得解得
故二次函数的表达式为y=x2-2x-3. (3分)
(2)设M(x,x-3),则P(x,x2-2x-3).
①线段PM有最大值. (4分)
PM=(x-3)-(x2-2x-3)=-(x-)2+.
∵-1<0,
∴PM有最大值.
当x=时,PM最大为. (6分)
②存在. (7分)
PM2=(x-3-x2+2x+3)2=(-x2+3x)2,
PC2=x2+(-3-x2+2x+3)2=x2+(2x-x2)2,
MC2=(x-3+3)2+x2=2x2.
当PM=PC时,(-x2+3x)2=x2+(2x-x2)2,
解得x1=2,x2=0(舍去),
∴P(2,-3). (8分)
当PM=MC时,(-x2+3x)2=2x2,
解得x1=3-,x2=0(舍去),x3=3+(舍去),
∴P(3-,2-4). (9分)
综上,点P的坐标为(2,-3)或(3-,2-4). (10分)
高分锦囊
探究二次函数中线段问题的一般方法
二次函数中线段问题一般分三类,具体如下.
(1)线段的数量关系问题.此类问题一般是求满足线段数量关系的点的坐标.针对这种情况,应先在图中找出对应线段, 弄清已知点和未知点,再联系二次函数和一次函数,设出未知点的坐标,使其只含一个未知数,最后用含未知数的代数式表示出线段的长度,列出满足线段数量关系的等式,进而求出未知数的值.
(2)线段最值问题.此类问题通常有两类:①设出未知数(通常是一个与所求线段关系紧密的点的横坐标),通过题目中的函数关系,用未知数表示出有关线段端点的坐标,进而表示出线段的长,利用二次函数的性质求最值,从而得到线段的最大值或最小值;②在求线段的和最小值或差最大值的时候可以利用轴对称模型,通常是作定点关于动点所在直线的对称点,连接对称点与另一个定点(或连接两个对称点)的线段的长即为所求的最值.
(3)周长最值问题.此类问题一般为对含动点的图形求周长的最值,解决此类问题时应利用转化思想,即先观察图形,结合题目分清楚定线段和不定线段,然后将求周长的最值转化为求不定线段和的最值,其方法同2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)