2024沪科版九年级数学下学期单元测试卷--第26章 概率初步(含答案)
文档属性
| 名称 | 2024沪科版九年级数学下学期单元测试卷--第26章 概率初步(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024沪科版九年级数学下学期单元测试卷
第26章 概率初步
时间:120分钟 满分:150分
题号 一 二 三 四 五 六 七 八 评价
错题
一、选择题(本大题共10小题,每小题4分,满分40分.每小题有四个选项,其中只有一个选项符合题意)
1.下列事件中,是随机事件的是 ( )
A.在1个标淮大气压下,加热到100 ℃时,水沸腾
B.购买一张彩票,中奖
C.任意画一个三角形,其内角和是360°
D.明天太阳从东方升起
2.(2021·江苏泰州中考)“14人中至少有2人在同一个月过生日”这一事件发生的概率为P,则 ( )
A.P=0 B.01
3.(2022·安徽芜湖期中)为做好课后服务工作,学校组织开展网上答疑活动,在某时间段开放3个数学教室,3个语文教室,2个英语教室.随机进入一个网络教室,则该教室是数学教室的概率为 ( )
A. B. C. D.
4.从一副54张的扑克牌中随意抽出一张,给出以下4个事件:①抽到大王;②抽到小王;③抽到2;④抽到梅花.其中发生的可能性最大的是 ( )
A.① B.② C.③ D.④
5.有一则笑话:妈妈给一对双胞胎洗澡,先洗哥哥,再洗弟弟,刚把两人洗完,就听到两个小家伙在床上笑.“你们笑什么 ”妈妈问.“妈妈!您给弟弟洗了两回,可是还没给我洗呢!”哥哥回答.此事件发生的概率为 ( )
A. B. C. D.1
6.(2021·江苏无锡滨湖区期中)下列关于概率的说法正确的是 ( )
A.因为抛掷一枚图钉不是“钉尖着地”就是“钉尖不着地”(如图所示),所以“钉尖着地”的概率是0.5
B.小明前几次的数学测试成绩都在90分以上,小明这次的数学测试成绩也一定在90分以上
C.小明投篮投中的概率是60%,这表明小明平均每投篮10次,可能会投中6次
D.随机事件发生的频率就是该事件发生的概率
7.(2022·四川南充期末)在如图所示的电路图中,随机闭合开关S1,S2,S3中的两个,能让灯泡L1发光的概率是 ( )
A. B. C. D.
8.(2022·山东青岛期中)甲、乙两名同学在一次用频率估计概率的试验中,统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是 ( )
A.掷一枚质地均匀的正六面体的骰子,出现5点的概率
B.在“石头、剪刀、布”的游戏中,小明随机出“剪刀”的概率
C.掷一枚质地均匀的硬币,出现反面朝上的概率
D.从一个装有1个红球和2个白球的袋子中任意摸出一个球,摸到白球的概率
9.(2021·安徽中考)如图,在由三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以围成一个矩形,从这些矩形中任选一个,则所选矩形含点A的概率是 ( )
A. B. C. D.
10.(2021·浙江嘉兴中考改编)看了《田忌赛马》故事后,小杨用数学模型来分析:齐王与田忌的上中下三个等级的3匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的3匹马出场顺序为上等马、中等马、下等马.若田忌的3匹马随机出场,则田忌能赢得比赛的概率为 ( )
马匹
下等马 中等马 上等马
姓 名 齐王 6 8 10
田忌 5 7 9
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.某班级中有男生和女生各若干,若随机抽取一人,抽到男生的概率是, 则抽到女生的概率是 .
12.(2022·浙江杭州期中)一个布袋里装有2个只有颜色不同的球,其中1个红球,1个白球.从布袋里摸出1个球,记下颜色后放回,搅匀,再摸出1个球,则两次摸到的球中1个是白球1个是红球的概率是 .
13.欧阳修在《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”.如图,可见卖油翁的技艺之高超,若铜钱直径为4 cm,中间有边长为1 cm的正方形小孔,随机向铜钱上滴一滴油(油滴大小忽略不计),则油滴恰好落入孔中的概率是 .
14.(2022·重庆南岸区期中)四张背面相同的卡片,分别标记有-1,1,2,3的数,洗匀后背面朝上,先从中抽取一张,把抽到的卡片上的数记为a,不放回,再从剩下的卡片中抽取一张,把抽到的卡片上的数记为c,则抛物线y=ax2+c与x轴有交点的概率为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12.
13. 14.
三、(本大题共2小题,每小题8分,满分16分)
15.(2021·陕西西安碑林区模拟)甲、乙两名医生各自选择到A,B,C三个接种点中的一个进行新冠疫苗的接种工作.
(1)写出甲、乙两名医生随机选择接种点的所有可能出现的结果(用A,B表示即可)
(2)求甲、乙两名医生随机选到同一个接种点的概率.
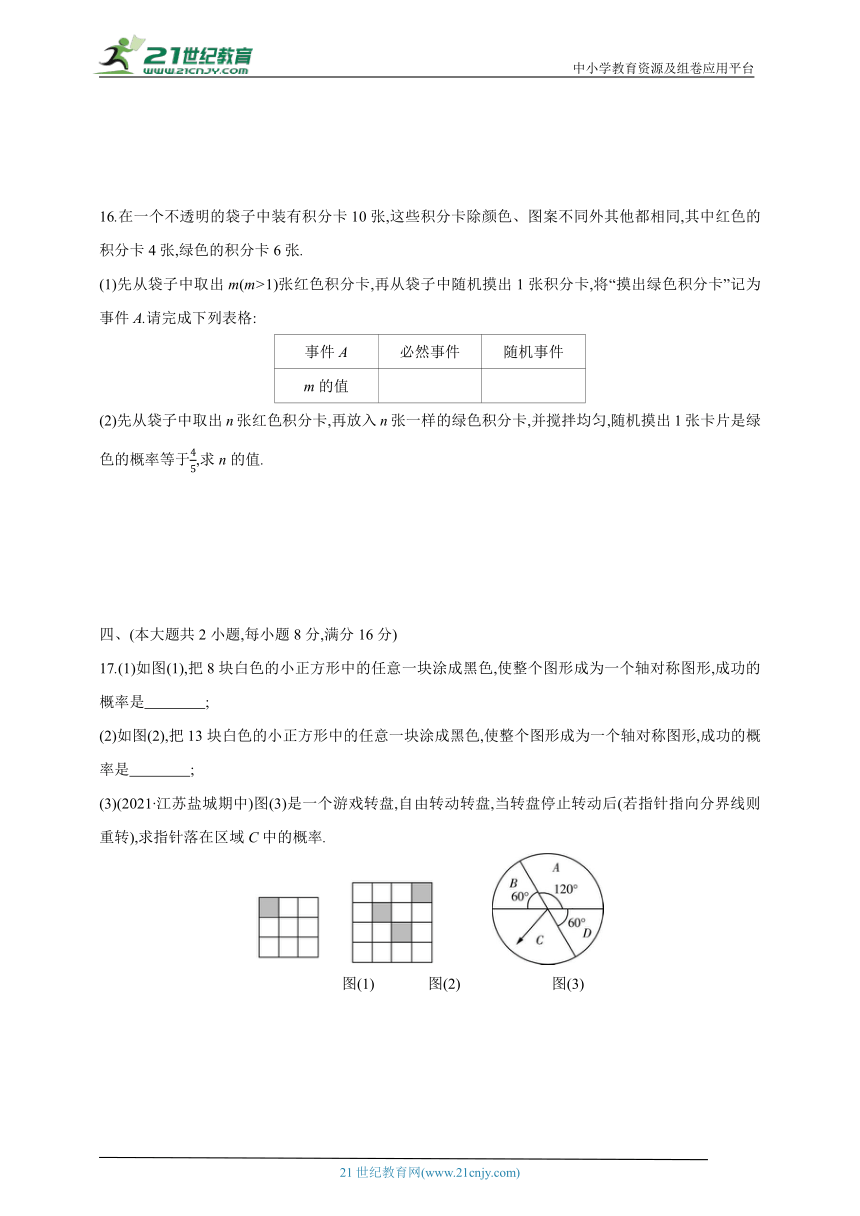
16.在一个不透明的袋子中装有积分卡10张,这些积分卡除颜色、图案不同外其他都相同,其中红色的积分卡4张,绿色的积分卡6张.
(1)先从袋子中取出m(m>1)张红色积分卡,再从袋子中随机摸出1张积分卡,将“摸出绿色积分卡”记为事件A.请完成下列表格:
事件A 必然事件 随机事件
m的值
(2)先从袋子中取出n张红色积分卡,再放入n张一样的绿色积分卡,并搅拌均匀,随机摸出1张卡片是绿色的概率等于,求n的值.
四、(本大题共2小题,每小题8分,满分16分)
17.(1)如图(1),把8块白色的小正方形中的任意一块涂成黑色,使整个图形成为一个轴对称图形,成功的概率是 ;
(2)如图(2),把13块白色的小正方形中的任意一块涂成黑色,使整个图形成为一个轴对称图形,成功的概率是 ;
(3)(2021·江苏盐城期中)图(3)是一个游戏转盘,自由转动转盘,当转盘停止转动后(若指针指向分界线则重转),求指针落在区域C中的概率.
图(1) 图(2) 图(3)
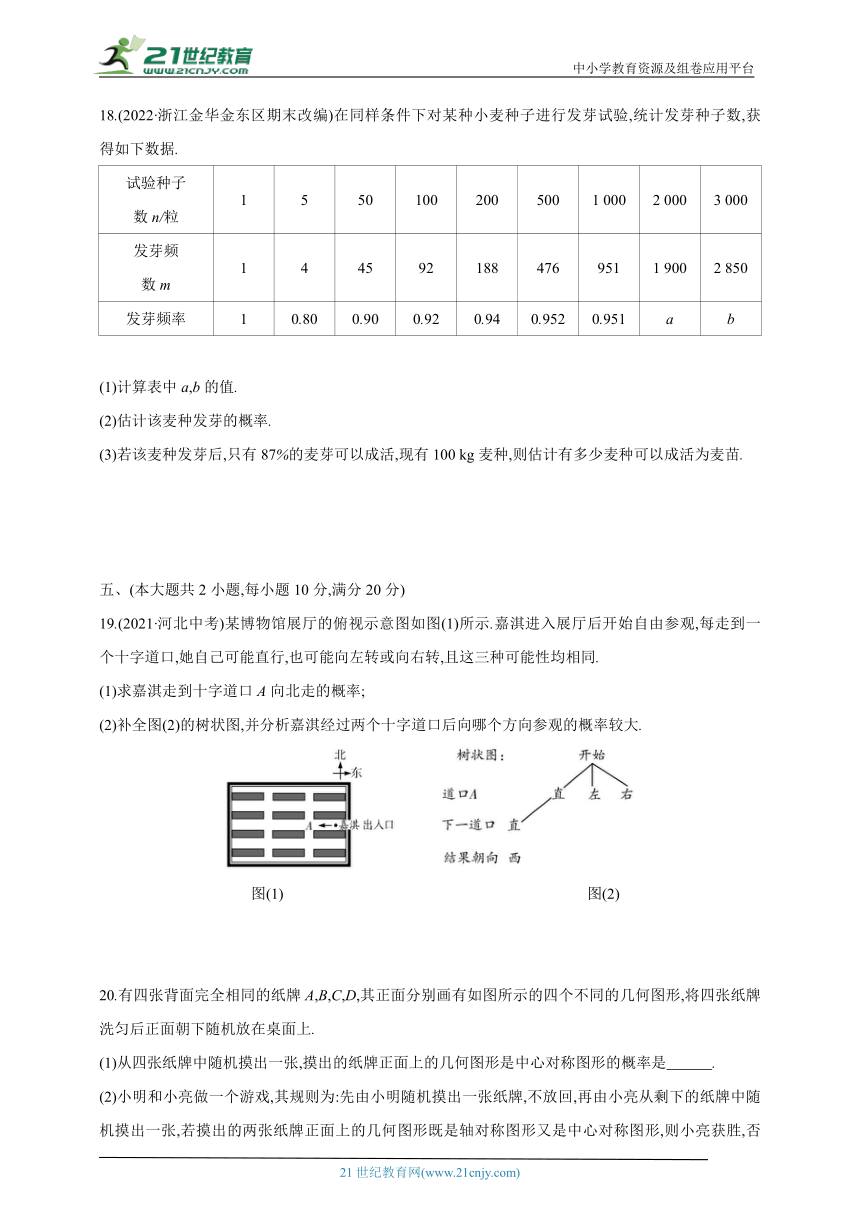
18.(2022·浙江金华金东区期末改编)在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下数据.
试验种子 数n/粒 1 5 50 100 200 500 1 000 2 000 3 000
发芽频 数m 1 4 45 92 188 476 951 1 900 2 850
发芽频率 1 0.80 0.90 0.92 0.94 0.952 0.951 a b
(1)计算表中a,b的值.
(2)估计该麦种发芽的概率.
(3)若该麦种发芽后,只有87%的麦芽可以成活,现有100 kg麦种,则估计有多少麦种可以成活为麦苗.
五、(本大题共2小题,每小题10分,满分20分)
19.(2021·河北中考)某博物馆展厅的俯视示意图如图(1)所示.嘉淇进入展厅后开始自由参观,每走到一个十字道口,她自己可能直行,也可能向左转或向右转,且这三种可能性均相同.
(1)求嘉淇走到十字道口A向北走的概率;
(2)补全图(2)的树状图,并分析嘉淇经过两个十字道口后向哪个方向参观的概率较大.
图(1) 图(2)
20.有四张背面完全相同的纸牌A,B,C,D,其正面分别画有如图所示的四个不同的几何图形,将四张纸牌洗匀后正面朝下随机放在桌面上.
(1)从四张纸牌中随机摸出一张,摸出的纸牌正面上的几何图形是中心对称图形的概率是 .
(2)小明和小亮做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张纸牌正面上的几何图形既是轴对称图形又是中心对称图形,则小亮获胜,否则小明获胜.这个游戏公平吗 请用列表法或画树状图法说明理由.若不公平,请你帮忙修改一下游戏规则,使游戏公平.
六、(本题满分12分)
21. (2021·浙江湖州期中)若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).从由数字1,2,3,4,5,6构成的所有“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)写出所有个位数字是5的“两位递增数”.
(2)请用列表法或画树状图法,求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率.
七、(本题满分12分)
22.体育课上,小明、小强、小华三人在踢足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,踢了两次后,求足球踢到小华处的概率;
(2)如果踢了三次后,球踢到小明处的可能性最小,应从谁开始踢 请说明理由.
八、(本题满分14分)
23.甲乙两人玩数字游戏,先由甲写一个数字,再由乙猜甲写的数字.要求:他们写和猜的数字只在1,2,3,4,5这五个数字中.
(1)请用列表法或画树状图法表示出他们写和猜的所有情况;
(2)如果他们写和猜的数字相同,那么称他们“心灵相通”,求他们“心灵相通”的概率;
(3)将甲写的数字记为a,乙猜的数字记为b,如果他们写和猜的数字满足|a-b|≤1,那么称他们“心有灵犀”,求他们“心有灵犀”的概率.
第26章 概率初步
1 2 3 4 5 6 7 8 9 10
B C B D A C D B D A
11. 12.
13. 14.
1.B 在1个标准大气压下,水沸腾的温度是100 ℃,所以选项A是必然事件;买彩票中奖是随机事件;任意一个三角形,它的内角和都是180°,所以选项C是不可能事件;太阳每天都从东方升起,故选项D是必然事件.
2.C “14人中至少有2人在同一个月过生日”这一事件为必然事件,∴这一事件发生的概率为1.
3.B 根据题意可知,共开放了3+3+2=8(个)网络教室,则随机进入数学教室的概率为.
4.D 一副54张的扑克牌中,有1张大王,1张小王,4张2,13张梅花.因为13>4>1,所以这4个事件发生的可能性最大的是④.故选D.
5.A 将双胞胎哥哥和弟弟分别用M,N表示,妈妈给双胞胎洗澡的情况有MM,NN,MN,NM,共4种,故给弟弟洗两回的事件发生的概率为,故选A.
6.C 因为图钉上、下不一样,所以钉尖着地的概率和钉尖不着地的概率不相同,故A选项不正确;小明前几次的数学测试成绩都在90分以上,小明这次的数学测试成绩不一定在90分以上,故B选项不正确;小明投篮投中的概率是60%,这表明小明平均每投篮10次,可能会投中6次,故C选项正确;随机事件的频率只是概率的近似值,它不一定等于概率,故D选项不正确.
7.D 根据题意画出树状图如下.
由树状图可知,共有6种等可能的情况,其中能让灯泡L1发光的情况有2种,即S1S2,S2S1,所以能让灯泡L1发光的概率为=.
8.B 根据统计图可知,试验结果出现的频率在0.33附近波动,所以可估计其概率为0.33.掷一枚质地均匀的正六面体的骰子,出现5点的概率为,故A选项不符合题意;在“石头、剪刀、布”的游戏中,小明随机出“剪刀”的概率为≈0.33,故B选项符合题意;掷一枚质地均匀的硬币,出现反面朝上的概率为,故C选项不符合题意;从一个装有1个红球和2个白球的袋子中任意摸出一个球,摸到白球的概率是=≈0.67,故D选项不符合题意.
9.D 如图,任选两条横线和两条竖线共可以围成9个不同的矩形,其中含点A的矩形有4个,故从这些矩形中任选一个,所选矩形含点A的概率是.
10.A 由于田忌的上、中等马分别比齐王的中、下等马强,当齐王的3匹马出场顺序为上等马、中等马、下等马时,田忌的马按下等马、上等马、中等马的顺序出场,田忌才能赢得比赛.当田忌的3匹马随机出场时,双方马的对阵情况如下.
齐王 的马 上中下 上中下 上中下 上中下 上中下 上中下
田忌 的马 上中下 上下中 中上下 中下上 下上中 下中上
双方马的对阵中,共有6种等可能的对阵情况,只有1种对阵情况田忌能赢,∴田忌能赢得比赛的概率为.
11.
12. 画树状图如下.
由树状图知,共有4种等可能的结果,两次摸到的球中1个是白球1个是红球的结果有2种,∴两次摸到的球中1个是白球1个是红球的概率为.
13. 油滴恰好落入孔中的概率为=.
14. ∵抛物线y=ax2+c与x轴有交点,∴令ax2+c=0,Δ=02-4ac≥0,解得ac≤0. 画树状图如下.
由树状图可知,共有12种等可能的结果.其中ac≤0的结果有6种,∴抛物线y=ax2+c与x轴有交点的概率为=.
15.【参考答案】(1)AA,AB,AC,BA,BB,BC,CA,CB,CC. (4分)
(2)由(1)得,共有9种等可能的结果,其中甲、乙两名医生随机选到同一个接种点的有3种,则甲、乙两名医生随机选到同一个接种点的概率是=. (8分)
16.【参考答案】(1)4 2或3 (4分)
解法提示:若事件A为必然事件,则袋中应全为绿色卡片,所以m=4;
若事件A为随机事件,则袋中应有红色卡片,
∵m>1,
∴m=2或m=3.
(2)由题意可得,=,
解得n=2. (8分)
17.【参考答案】(1) (3分)
解法提示:
①
②
③ ④
(2) 解法提示:
①
②
③
(5分)
(3)由题意知,区域C的圆心角度数为360°-(60°+120°+60°)=120°.
把区域C,区域A都分成两个圆心角为60°的扇形,则共有6种等可能的结果,其中落在区域C的结果有2种,
故指针落在区域C中的概率为=. (8分)
18.【参考答案】(1)a=1 900÷2 000=0.95,b=2 850÷3 000=0.95. (4分)
(2)观察发现:随着大量重复试验,发芽频率逐渐稳定到常数0.95附近,
所以估计该麦种发芽的概率为0.95. (6分)
(3)100×0.95×87%=82.65(kg).
答:估计有82.65 kg的麦种可以成活为麦苗. (8分)
19.【参考答案】(1)∵当嘉淇走到道口A时,有直、左、右3种等可能结果,只有向右转为北,
∴P(嘉淇向北走)=. (4分)
(2)补全树状图如下. (6分)
由树状图可知,所有等可能的结果有9种,其中朝向东2种,朝向西3种,朝向南2种,朝向北2种.
∴P(朝西)==>P(朝东)=P(朝南)=P(朝北)=, (9分)
∴嘉淇经过两个十字道口后向西参观的概率较大.(10分)
20.【参考答案】(1) (3分)
(2)游戏不公平. (4分)
理由:列表如下.
第二次 第一次
A B C D
A (B,A) (C,A) (D,A)
B (A,B) (C,B) (D,B)
C (A,C) (B,C) (D,C)
D (A,D) (B,D) (C,D)
由表可得,共有12种等可能的结果,其中摸出的两张纸牌正面上的几何图形既是轴对称图形又是中心对称图形的结果有2种,即(A,C)和(C,A),
所以P(两张纸牌正面上的几何图形既是轴对称图形又是中心对称图形)==≠,
所以游戏不公平. (8分)
修改规则:若抽到的两张纸牌正面上的几何图形都是中心对称图形,则小明获胜,否则小亮获胜.(答案不唯一) (10分)
21.【参考答案】(1)根据题意,所有个位数字是5的“两位递增数”有15,25,35,45. (5分)
(2)画树状图如下:
(8分)
由树状图可知,共有15种等可能的结果,其中个位数字与十位数字之积能被10整除的结果有3种,分别是25,45,56,
所以个位数字与十位数字之积能被10整除的概率==. (12分)
22.【参考答案】(1)画树状图如下:
由树状图可知,所有等可能的情况有4种,踢两次后,足球踢到小华处的情况有1种,
所以P(足球踢到小华处)=. (5分)
(2)应从小明开始踢. (6分)
理由:用A,B,C表示这三个人.
从A开始踢,画树状图如下.
(9分)
解法① 由树状图可知,从A开始踢,P(踢到A处)==.
P(踢到B处)=,
P(踢到C处)=.
故A代表小明,即从小明开始踢,踢三次后,球踢到小明处的可能性最小. (12分)
解法② 由树状图可知,从A开始踢,共有8种等可能的结果,
踢三次后,球踢到A处的结果数最小,为2种,
故A代表小明,即从小明开始踢,踢三次后,球踢到小明处的可能性最小. (12分)
23.【参考答案】(1)列表如下:
乙
1 2 3 4 5
甲 1 (1,1) (1,2) (1,3) (1,4) (1,5)
2 (2,1) (2,2) (2,3) (2,4) (2,5)
3 (3,1) (3,2) (3,3) (3,4) (3,5)
4 (4,1) (4,2) (4,3) (4,4) (4,5)
5 (5,1) (5,2) (5,3) (5,4) (5,5)
(4分)
(2)根据(1)中表格可知共有25种等可能的结果,其中他们写和猜的数字相同的情况一共有5种,则他们“心灵相通”的概率为=. (8分)
(3)所有满足条件的a,b的值如下:
①若a=1,则b=1,2;
②若a=2,则b=1,2,3;
③若a=3,则b=2,3,4;
④若a=4,则b=3,4,5;
⑤若a=5,则b=4,5.
综上可知,结果共有2+3+3+3+2=13(种), 所以他们“心有灵犀”的概率为. (14分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024沪科版九年级数学下学期单元测试卷
第26章 概率初步
时间:120分钟 满分:150分
题号 一 二 三 四 五 六 七 八 评价
错题
一、选择题(本大题共10小题,每小题4分,满分40分.每小题有四个选项,其中只有一个选项符合题意)
1.下列事件中,是随机事件的是 ( )
A.在1个标淮大气压下,加热到100 ℃时,水沸腾
B.购买一张彩票,中奖
C.任意画一个三角形,其内角和是360°
D.明天太阳从东方升起
2.(2021·江苏泰州中考)“14人中至少有2人在同一个月过生日”这一事件发生的概率为P,则 ( )
A.P=0 B.0
3.(2022·安徽芜湖期中)为做好课后服务工作,学校组织开展网上答疑活动,在某时间段开放3个数学教室,3个语文教室,2个英语教室.随机进入一个网络教室,则该教室是数学教室的概率为 ( )
A. B. C. D.
4.从一副54张的扑克牌中随意抽出一张,给出以下4个事件:①抽到大王;②抽到小王;③抽到2;④抽到梅花.其中发生的可能性最大的是 ( )
A.① B.② C.③ D.④
5.有一则笑话:妈妈给一对双胞胎洗澡,先洗哥哥,再洗弟弟,刚把两人洗完,就听到两个小家伙在床上笑.“你们笑什么 ”妈妈问.“妈妈!您给弟弟洗了两回,可是还没给我洗呢!”哥哥回答.此事件发生的概率为 ( )
A. B. C. D.1
6.(2021·江苏无锡滨湖区期中)下列关于概率的说法正确的是 ( )
A.因为抛掷一枚图钉不是“钉尖着地”就是“钉尖不着地”(如图所示),所以“钉尖着地”的概率是0.5
B.小明前几次的数学测试成绩都在90分以上,小明这次的数学测试成绩也一定在90分以上
C.小明投篮投中的概率是60%,这表明小明平均每投篮10次,可能会投中6次
D.随机事件发生的频率就是该事件发生的概率
7.(2022·四川南充期末)在如图所示的电路图中,随机闭合开关S1,S2,S3中的两个,能让灯泡L1发光的概率是 ( )
A. B. C. D.
8.(2022·山东青岛期中)甲、乙两名同学在一次用频率估计概率的试验中,统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是 ( )
A.掷一枚质地均匀的正六面体的骰子,出现5点的概率
B.在“石头、剪刀、布”的游戏中,小明随机出“剪刀”的概率
C.掷一枚质地均匀的硬币,出现反面朝上的概率
D.从一个装有1个红球和2个白球的袋子中任意摸出一个球,摸到白球的概率
9.(2021·安徽中考)如图,在由三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以围成一个矩形,从这些矩形中任选一个,则所选矩形含点A的概率是 ( )
A. B. C. D.
10.(2021·浙江嘉兴中考改编)看了《田忌赛马》故事后,小杨用数学模型来分析:齐王与田忌的上中下三个等级的3匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的3匹马出场顺序为上等马、中等马、下等马.若田忌的3匹马随机出场,则田忌能赢得比赛的概率为 ( )
马匹
下等马 中等马 上等马
姓 名 齐王 6 8 10
田忌 5 7 9
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.某班级中有男生和女生各若干,若随机抽取一人,抽到男生的概率是, 则抽到女生的概率是 .
12.(2022·浙江杭州期中)一个布袋里装有2个只有颜色不同的球,其中1个红球,1个白球.从布袋里摸出1个球,记下颜色后放回,搅匀,再摸出1个球,则两次摸到的球中1个是白球1个是红球的概率是 .
13.欧阳修在《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”.如图,可见卖油翁的技艺之高超,若铜钱直径为4 cm,中间有边长为1 cm的正方形小孔,随机向铜钱上滴一滴油(油滴大小忽略不计),则油滴恰好落入孔中的概率是 .
14.(2022·重庆南岸区期中)四张背面相同的卡片,分别标记有-1,1,2,3的数,洗匀后背面朝上,先从中抽取一张,把抽到的卡片上的数记为a,不放回,再从剩下的卡片中抽取一张,把抽到的卡片上的数记为c,则抛物线y=ax2+c与x轴有交点的概率为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12.
13. 14.
三、(本大题共2小题,每小题8分,满分16分)
15.(2021·陕西西安碑林区模拟)甲、乙两名医生各自选择到A,B,C三个接种点中的一个进行新冠疫苗的接种工作.
(1)写出甲、乙两名医生随机选择接种点的所有可能出现的结果(用A,B表示即可)
(2)求甲、乙两名医生随机选到同一个接种点的概率.
16.在一个不透明的袋子中装有积分卡10张,这些积分卡除颜色、图案不同外其他都相同,其中红色的积分卡4张,绿色的积分卡6张.
(1)先从袋子中取出m(m>1)张红色积分卡,再从袋子中随机摸出1张积分卡,将“摸出绿色积分卡”记为事件A.请完成下列表格:
事件A 必然事件 随机事件
m的值
(2)先从袋子中取出n张红色积分卡,再放入n张一样的绿色积分卡,并搅拌均匀,随机摸出1张卡片是绿色的概率等于,求n的值.
四、(本大题共2小题,每小题8分,满分16分)
17.(1)如图(1),把8块白色的小正方形中的任意一块涂成黑色,使整个图形成为一个轴对称图形,成功的概率是 ;
(2)如图(2),把13块白色的小正方形中的任意一块涂成黑色,使整个图形成为一个轴对称图形,成功的概率是 ;
(3)(2021·江苏盐城期中)图(3)是一个游戏转盘,自由转动转盘,当转盘停止转动后(若指针指向分界线则重转),求指针落在区域C中的概率.
图(1) 图(2) 图(3)
18.(2022·浙江金华金东区期末改编)在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下数据.
试验种子 数n/粒 1 5 50 100 200 500 1 000 2 000 3 000
发芽频 数m 1 4 45 92 188 476 951 1 900 2 850
发芽频率 1 0.80 0.90 0.92 0.94 0.952 0.951 a b
(1)计算表中a,b的值.
(2)估计该麦种发芽的概率.
(3)若该麦种发芽后,只有87%的麦芽可以成活,现有100 kg麦种,则估计有多少麦种可以成活为麦苗.
五、(本大题共2小题,每小题10分,满分20分)
19.(2021·河北中考)某博物馆展厅的俯视示意图如图(1)所示.嘉淇进入展厅后开始自由参观,每走到一个十字道口,她自己可能直行,也可能向左转或向右转,且这三种可能性均相同.
(1)求嘉淇走到十字道口A向北走的概率;
(2)补全图(2)的树状图,并分析嘉淇经过两个十字道口后向哪个方向参观的概率较大.
图(1) 图(2)
20.有四张背面完全相同的纸牌A,B,C,D,其正面分别画有如图所示的四个不同的几何图形,将四张纸牌洗匀后正面朝下随机放在桌面上.
(1)从四张纸牌中随机摸出一张,摸出的纸牌正面上的几何图形是中心对称图形的概率是 .
(2)小明和小亮做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张纸牌正面上的几何图形既是轴对称图形又是中心对称图形,则小亮获胜,否则小明获胜.这个游戏公平吗 请用列表法或画树状图法说明理由.若不公平,请你帮忙修改一下游戏规则,使游戏公平.
六、(本题满分12分)
21. (2021·浙江湖州期中)若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).从由数字1,2,3,4,5,6构成的所有“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)写出所有个位数字是5的“两位递增数”.
(2)请用列表法或画树状图法,求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率.
七、(本题满分12分)
22.体育课上,小明、小强、小华三人在踢足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,踢了两次后,求足球踢到小华处的概率;
(2)如果踢了三次后,球踢到小明处的可能性最小,应从谁开始踢 请说明理由.
八、(本题满分14分)
23.甲乙两人玩数字游戏,先由甲写一个数字,再由乙猜甲写的数字.要求:他们写和猜的数字只在1,2,3,4,5这五个数字中.
(1)请用列表法或画树状图法表示出他们写和猜的所有情况;
(2)如果他们写和猜的数字相同,那么称他们“心灵相通”,求他们“心灵相通”的概率;
(3)将甲写的数字记为a,乙猜的数字记为b,如果他们写和猜的数字满足|a-b|≤1,那么称他们“心有灵犀”,求他们“心有灵犀”的概率.
第26章 概率初步
1 2 3 4 5 6 7 8 9 10
B C B D A C D B D A
11. 12.
13. 14.
1.B 在1个标准大气压下,水沸腾的温度是100 ℃,所以选项A是必然事件;买彩票中奖是随机事件;任意一个三角形,它的内角和都是180°,所以选项C是不可能事件;太阳每天都从东方升起,故选项D是必然事件.
2.C “14人中至少有2人在同一个月过生日”这一事件为必然事件,∴这一事件发生的概率为1.
3.B 根据题意可知,共开放了3+3+2=8(个)网络教室,则随机进入数学教室的概率为.
4.D 一副54张的扑克牌中,有1张大王,1张小王,4张2,13张梅花.因为13>4>1,所以这4个事件发生的可能性最大的是④.故选D.
5.A 将双胞胎哥哥和弟弟分别用M,N表示,妈妈给双胞胎洗澡的情况有MM,NN,MN,NM,共4种,故给弟弟洗两回的事件发生的概率为,故选A.
6.C 因为图钉上、下不一样,所以钉尖着地的概率和钉尖不着地的概率不相同,故A选项不正确;小明前几次的数学测试成绩都在90分以上,小明这次的数学测试成绩不一定在90分以上,故B选项不正确;小明投篮投中的概率是60%,这表明小明平均每投篮10次,可能会投中6次,故C选项正确;随机事件的频率只是概率的近似值,它不一定等于概率,故D选项不正确.
7.D 根据题意画出树状图如下.
由树状图可知,共有6种等可能的情况,其中能让灯泡L1发光的情况有2种,即S1S2,S2S1,所以能让灯泡L1发光的概率为=.
8.B 根据统计图可知,试验结果出现的频率在0.33附近波动,所以可估计其概率为0.33.掷一枚质地均匀的正六面体的骰子,出现5点的概率为,故A选项不符合题意;在“石头、剪刀、布”的游戏中,小明随机出“剪刀”的概率为≈0.33,故B选项符合题意;掷一枚质地均匀的硬币,出现反面朝上的概率为,故C选项不符合题意;从一个装有1个红球和2个白球的袋子中任意摸出一个球,摸到白球的概率是=≈0.67,故D选项不符合题意.
9.D 如图,任选两条横线和两条竖线共可以围成9个不同的矩形,其中含点A的矩形有4个,故从这些矩形中任选一个,所选矩形含点A的概率是.
10.A 由于田忌的上、中等马分别比齐王的中、下等马强,当齐王的3匹马出场顺序为上等马、中等马、下等马时,田忌的马按下等马、上等马、中等马的顺序出场,田忌才能赢得比赛.当田忌的3匹马随机出场时,双方马的对阵情况如下.
齐王 的马 上中下 上中下 上中下 上中下 上中下 上中下
田忌 的马 上中下 上下中 中上下 中下上 下上中 下中上
双方马的对阵中,共有6种等可能的对阵情况,只有1种对阵情况田忌能赢,∴田忌能赢得比赛的概率为.
11.
12. 画树状图如下.
由树状图知,共有4种等可能的结果,两次摸到的球中1个是白球1个是红球的结果有2种,∴两次摸到的球中1个是白球1个是红球的概率为.
13. 油滴恰好落入孔中的概率为=.
14. ∵抛物线y=ax2+c与x轴有交点,∴令ax2+c=0,Δ=02-4ac≥0,解得ac≤0. 画树状图如下.
由树状图可知,共有12种等可能的结果.其中ac≤0的结果有6种,∴抛物线y=ax2+c与x轴有交点的概率为=.
15.【参考答案】(1)AA,AB,AC,BA,BB,BC,CA,CB,CC. (4分)
(2)由(1)得,共有9种等可能的结果,其中甲、乙两名医生随机选到同一个接种点的有3种,则甲、乙两名医生随机选到同一个接种点的概率是=. (8分)
16.【参考答案】(1)4 2或3 (4分)
解法提示:若事件A为必然事件,则袋中应全为绿色卡片,所以m=4;
若事件A为随机事件,则袋中应有红色卡片,
∵m>1,
∴m=2或m=3.
(2)由题意可得,=,
解得n=2. (8分)
17.【参考答案】(1) (3分)
解法提示:
①
②
③ ④
(2) 解法提示:
①
②
③
(5分)
(3)由题意知,区域C的圆心角度数为360°-(60°+120°+60°)=120°.
把区域C,区域A都分成两个圆心角为60°的扇形,则共有6种等可能的结果,其中落在区域C的结果有2种,
故指针落在区域C中的概率为=. (8分)
18.【参考答案】(1)a=1 900÷2 000=0.95,b=2 850÷3 000=0.95. (4分)
(2)观察发现:随着大量重复试验,发芽频率逐渐稳定到常数0.95附近,
所以估计该麦种发芽的概率为0.95. (6分)
(3)100×0.95×87%=82.65(kg).
答:估计有82.65 kg的麦种可以成活为麦苗. (8分)
19.【参考答案】(1)∵当嘉淇走到道口A时,有直、左、右3种等可能结果,只有向右转为北,
∴P(嘉淇向北走)=. (4分)
(2)补全树状图如下. (6分)
由树状图可知,所有等可能的结果有9种,其中朝向东2种,朝向西3种,朝向南2种,朝向北2种.
∴P(朝西)==>P(朝东)=P(朝南)=P(朝北)=, (9分)
∴嘉淇经过两个十字道口后向西参观的概率较大.(10分)
20.【参考答案】(1) (3分)
(2)游戏不公平. (4分)
理由:列表如下.
第二次 第一次
A B C D
A (B,A) (C,A) (D,A)
B (A,B) (C,B) (D,B)
C (A,C) (B,C) (D,C)
D (A,D) (B,D) (C,D)
由表可得,共有12种等可能的结果,其中摸出的两张纸牌正面上的几何图形既是轴对称图形又是中心对称图形的结果有2种,即(A,C)和(C,A),
所以P(两张纸牌正面上的几何图形既是轴对称图形又是中心对称图形)==≠,
所以游戏不公平. (8分)
修改规则:若抽到的两张纸牌正面上的几何图形都是中心对称图形,则小明获胜,否则小亮获胜.(答案不唯一) (10分)
21.【参考答案】(1)根据题意,所有个位数字是5的“两位递增数”有15,25,35,45. (5分)
(2)画树状图如下:
(8分)
由树状图可知,共有15种等可能的结果,其中个位数字与十位数字之积能被10整除的结果有3种,分别是25,45,56,
所以个位数字与十位数字之积能被10整除的概率==. (12分)
22.【参考答案】(1)画树状图如下:
由树状图可知,所有等可能的情况有4种,踢两次后,足球踢到小华处的情况有1种,
所以P(足球踢到小华处)=. (5分)
(2)应从小明开始踢. (6分)
理由:用A,B,C表示这三个人.
从A开始踢,画树状图如下.
(9分)
解法① 由树状图可知,从A开始踢,P(踢到A处)==.
P(踢到B处)=,
P(踢到C处)=.
故A代表小明,即从小明开始踢,踢三次后,球踢到小明处的可能性最小. (12分)
解法② 由树状图可知,从A开始踢,共有8种等可能的结果,
踢三次后,球踢到A处的结果数最小,为2种,
故A代表小明,即从小明开始踢,踢三次后,球踢到小明处的可能性最小. (12分)
23.【参考答案】(1)列表如下:
乙
1 2 3 4 5
甲 1 (1,1) (1,2) (1,3) (1,4) (1,5)
2 (2,1) (2,2) (2,3) (2,4) (2,5)
3 (3,1) (3,2) (3,3) (3,4) (3,5)
4 (4,1) (4,2) (4,3) (4,4) (4,5)
5 (5,1) (5,2) (5,3) (5,4) (5,5)
(4分)
(2)根据(1)中表格可知共有25种等可能的结果,其中他们写和猜的数字相同的情况一共有5种,则他们“心灵相通”的概率为=. (8分)
(3)所有满足条件的a,b的值如下:
①若a=1,则b=1,2;
②若a=2,则b=1,2,3;
③若a=3,则b=2,3,4;
④若a=4,则b=3,4,5;
⑤若a=5,则b=4,5.
综上可知,结果共有2+3+3+3+2=13(种), 所以他们“心有灵犀”的概率为. (14分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
