2024沪科版九年级数学下学期单元测试卷--第24章 圆(含答案)
文档属性
| 名称 | 2024沪科版九年级数学下学期单元测试卷--第24章 圆(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024沪科版九年级数学下学期单元测试卷
第24章 圆
时间:120分钟 满分:150分
题号 一 二 三 四 五 六 七 八 评价
错题
一、选择题(本大题共10小题,每小题4分,满分40分.每小题有四个选项,其中只有一个选项符合题意)
1.中华文化博大精深,以下是“育”“才”“水”“井”四字的甲骨文,其中是中心对称、但非轴对称图形的是 ( )
A B C D
2.(2022·河南漯河期中)如图,将△ABC绕点A逆时针旋转100°得到△ADE,若点D在线段BC的延长线上,则∠ADE= ( )
A.60° B.50° C.45° D.40°
(第2题) (第3题)
3.(2021·福建福州期中)如图,AB是☉O的直径,点C,D在☉O上,∠BDC=21°,则∠AOC= ( )
A.136° B.137° C.138° D.139°
4.(2021·江苏苏州期中)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是
A(-3,0),B(-1,2),C(3,2),则△ABC的外心的坐标是 ( )
A.(1,-2) B.(0,0) C.(1,-1) D.(0,-1)
(第4题) (第5题)
5.如图,四边形ABCD是☉O的内接四边形,若∠BAC=35°,∠CBD=70°,则∠BCD的度数为 ( )
A.70° B.75° C.80° D.85°
6.(2022·浙江金华期中改编)如图,☉O与正六边形OABCDE的边OA,OE分别交于点F,G,点M为劣弧FG的中点.连接FM,GM,若FM=2,则☉O的半径为 ( )
A.2 B. C.2 D.2
7.一个圆锥的侧面积恰好等于其底面积的2倍,则该圆锥的侧面展开图所对应扇形的圆心角的度数为 ( )
A.180° B.90° C.120° D.60°
8.如图,已知点O是△ABC的内切圆的圆心,若∠BOC=124°,则∠A= ( )
A.56° B.60° C.62° D.68°
9.(2021·河南焦作期末)如图,四边形ABCD内接于☉O,AD∥BC,直线EF是☉O的切线,B是切点.若∠C=80°,∠ADB=54°,则∠CBF= ( )
A.45° B.46° C.54° D.60°
(第9题) (第10题)
10.如图,MN是☉O的直径,=,点B是劣弧AN的中点,点P是直径MN上一动点.连接AB,若MN=2,AB=-1,则△PAB的周长的最小值是 ( )
A.+1 B.+3 C.2 D.4
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(2022·广东广州海珠区期中改编)如图,E是正方形ABCD的边BC上一点,则△ABE绕点 逆时针至少旋转 后能够与△ADF重合.
(第11题) (第12题)
12.(2022·北京东城区期中)如图,AB是☉O的直径,AC是☉O的切线,A为切点,BC与☉O交于点D,连接OD.若∠C=50°,则∠AOD的度数为 .
13.(2022·江苏盐城景山中学月考)如图,正方形ABCD的边长为2,O为对角线的交点,点E,F分别为BC,AD的中点.以C为圆心,2为半径作,再分别以E,F为圆心,1为半径作,,则图中阴影部分的面积为 .(结果保留π)
(第13题) (第14题)
14.(2022·河北唐山丰南区联考改编)如图,P是抛物线y=-x2-4x-3上的一点,以点P为圆心、1个单位长度为半径作☉P,当☉P与x轴相切时,点P的坐标为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12.
13. 14.
三、(本大题共2小题,每小题8分,满分16分)
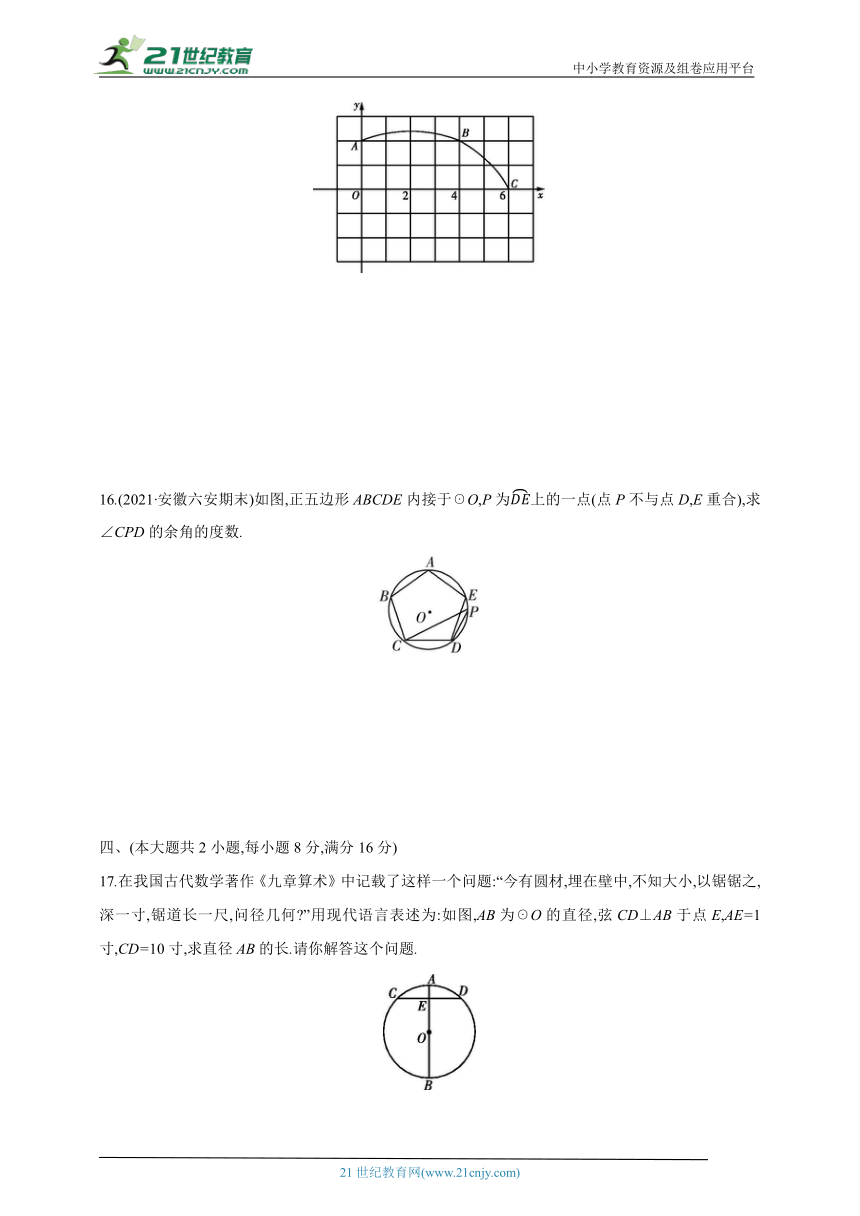
15.(2022·湖南长沙期末改编)如图,在正方形网格图中建立一个平面直角坐标系,一条圆弧经过网格点A(0,2),B(4,2),C(6,0).
(1)请在图中标出该圆弧所在圆的圆心D的位置并写出其坐标;
(2)连接AD,CD,求弧AC的长.(结果保留π)
16.(2021·安徽六安期末)如图,正五边形ABCDE内接于☉O,P为上的一点(点P不与点D,E重合),求∠CPD的余角的度数.
四、(本大题共2小题,每小题8分,满分16分)
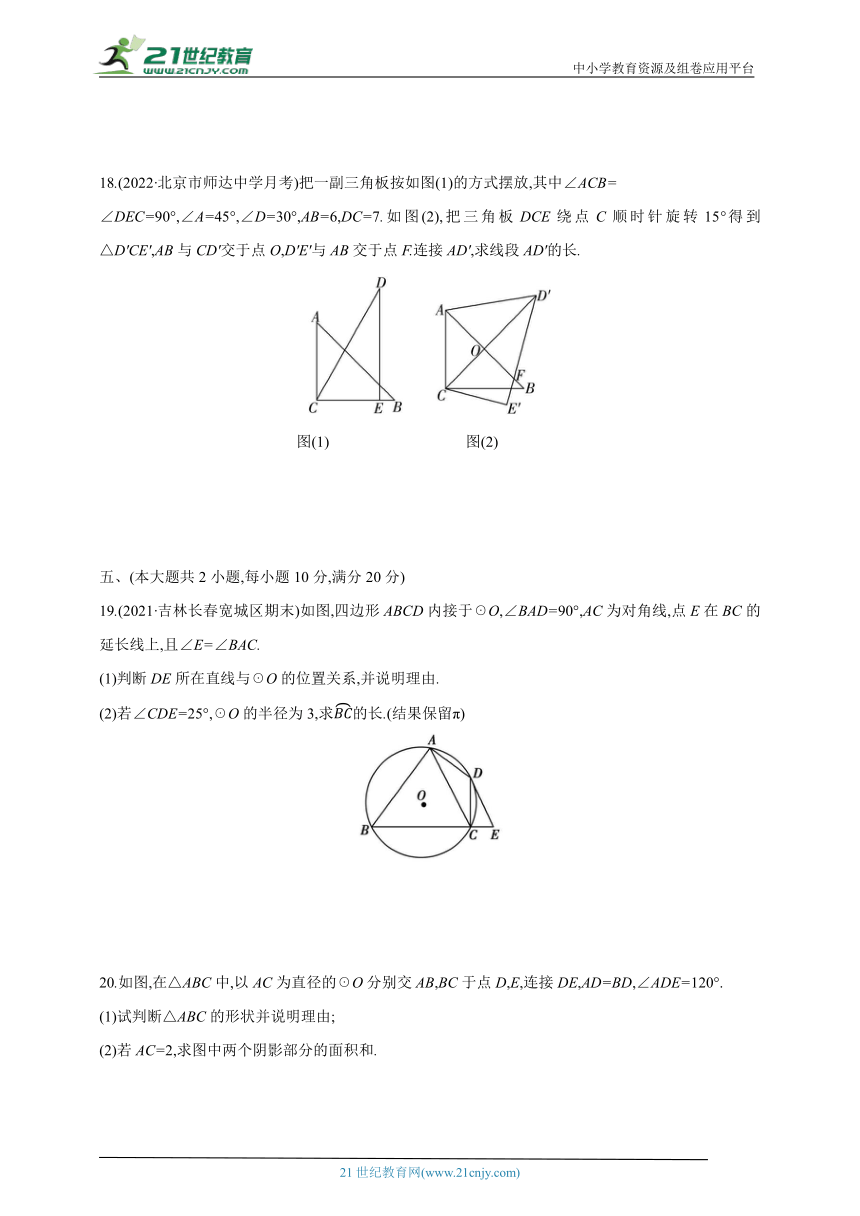
17.在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何 ”用现代语言表述为:如图,AB为☉O的直径,弦CD⊥AB于点E,AE=1寸,CD=10寸,求直径AB的长.请你解答这个问题.
18.(2022·北京市师达中学月考)把一副三角板按如图(1)的方式摆放,其中∠ACB=
∠DEC=90°,∠A=45°,∠D=30°,AB=6,DC=7.如图(2),把三角板DCE绕点C顺时针旋转15°得到△D'CE',AB与CD'交于点O,D'E'与AB交于点F.连接AD',求线段AD'的长.
图(1) 图(2)
五、(本大题共2小题,每小题10分,满分20分)
19.(2021·吉林长春宽城区期末)如图,四边形ABCD内接于☉O,∠BAD=90°,AC为对角线,点E在BC的延长线上,且∠E=∠BAC.
(1)判断DE所在直线与☉O的位置关系,并说明理由.
(2)若∠CDE=25°,☉O的半径为3,求的长.(结果保留π)
20.如图,在△ABC中,以AC为直径的☉O分别交AB,BC于点D,E,连接DE,AD=BD,∠ADE=120°.
(1)试判断△ABC的形状并说明理由;
(2)若AC=2,求图中两个阴影部分的面积和.
六、(本题满分12分)
21.如图,AB与☉O相切于点B,AO交☉O于点C,AO的延长线交☉O于点D,E是上不与B,D重合的点,sin A=.
(1)求∠BED的大小;
(2)若☉O的半径为3,点F在AB的延长线上,且BF=3,求证:DF与☉O相切.
七、(本题满分12分)
22.如图(1),AB是☉O的直径,点C在AB的延长线上,AB=4,BC=2,P是☉O上半部分的一个动点,连接OP,CP.
(1)求△OPC的最大面积;
(2)求∠OCP的最大度数;
(3)如图(2),延长PO交☉O于点D,连接DB.当CP=DB时,求证:CP是☉O的切线.
图(1) 图(2)
八、(本题满分14分)
23.【问题呈现】阿基米德折弦定理:如图(1),AB和BC是☉O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是的中点,则从点M向BC作垂线,垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的部分证明过程.
图(1) 图(2) 图(3) 图(4)
证明:如图(2),在CB上截取CG=AB,连接MA,MB,MC,MG.
∵M是的中点,∴=,∴MA=MC.
……
请按照上面的证明思路,写出该证明的剩余部分.
【实践应用】
(1)如图(3),已知△ABC内接于☉O,BC>AB>AC,D是的中点,请你依据阿基米德折弦定理直接写出图中某三条线段之间的数量关系;
(2)如图(4),已知等腰三角形ABC内接于☉O,AB=AC,D为上一点,连接DB,DC,∠ACD=45°,AE⊥CD于点E,△BDC的周长为4+2,BC=2,请求出AC的长.
第24章 圆
1 2 3 4 5 6 7 8 9 10
C D C A B C A D B A
11.A 90° 12.80°
13.π-2 14.(-2,1),(-2-,-1)或(-2+,-1)
1.C
2.D 连接CD,因为点D在线段BC的延长线上,所以点B,C,D共线.根据旋转可知,AB=AD,
∠B=∠ADE,∠BAD=100°,∴∠B=∠ADB=×(180°-100°)=40°,∴∠ADE=∠B=40°.
3.C ∵∠BOC=2∠BDC,∠BDC=21°,∴∠BOC=42°,∴∠AOC=180°-42°=138°.
4.A ∵三角形的外心到三角形三个顶点的距离相等,∴线段BC,AB的垂直平分线的交点即为外心P,由图可知,点P的坐标为(1,-2).
5.B 由圆周角定理得∠CAD=∠CBD=70°,∴∠BAD=70°+35°=105°.∵四边形ABCD是☉O的内接四边形,∴∠BCD=180°-∠BAD=75°.
6.C 如图,连接OM,由题意知∠FOG=120°.∵点M为劣弧FG的中点,∴∠FOM=60°,OM=OF,∴△OFM是等边三角形,∴OM=OF=FM=2,则☉O的半径为2,故选C.
7.A 设该圆锥的母线长为R,圆锥的侧面展开图所对应扇形的圆心角的度数为n°,底面圆的半径为r,则底面圆的周长为2πr,底面圆的面积为πr2,该扇形的侧面积为×2πr×R=πRr.已知πRr=2×πr2,所以R=2r.因为扇形弧长=底面圆周长,所以=2πr, 解得n=180.
8.D ∵∠BOC=124°,∴∠OBC+∠OCB=180°-124°=56°.∵点O是△ABC的内切圆的圆心,∴OB,OC分别平分∠ABC和∠ACB,∴∠ABC=2∠OBC,∠ACB=2∠OCB,∴∠ABC+∠ACB=2(∠OBC+∠OCB)=112°,∴∠A=
180°-112°=68°.
9.B 如图,连接OD,OB,则∠BOD=2∠C=160°.∵OB=OD,∴∠OBD==10°.∵四边形ABCD内接于☉O,∴∠A=180°-∠C=100°.∵AD∥BC,∴∠DBC=∠ADB=54°,∴∠OBC=54°-10°=44°.∵EF是☉O的切线,
∴∠OBF=90°,∴∠CBF=90°-∠OBC=90°-44°=46°.故选B.
(第9题) (第10题)
10.A (将军饮马模型)如图,作点A关于MN的对称点A',连接A'B,交MN于点P,连接OA',OA,OB,PA.
∵点A与点A'关于MN对称,∴PA=PA'.由题意知∠A'ON=∠AON=60°.∵点B是劣弧AN的中点,
∴∠BON=30°,∴∠A'OB=∠A'ON+∠BON=90°.又OA=OA'=MN=,∴A'B=2,∴PA+PB=PA'+
PB=A'B=2.∵AB=-1,∴△PAB的周长的最小值是2+-1=+1.故选A.
11.A 90°
12.80° 由题意知∠CAB=90°.∵∠C=50°,∴∠ABC=90°-50°=40°.又OB=OD,∴∠ODB=∠OBD=40°,
∴∠AOD=∠OBD+∠ODB=40°+40°=80°.
13.π-2 (转化思想)连接BD,将不规则的阴影图形通过割补法转换成弓形BD,由题意知,阴影部分的面
积=S扇形CBD-S△BCD=π×22-×2×2=π-2.
14.(-2,1),(-2-,-1)或(-2+,-1) (分类讨论思想)如图,分两种情况讨论.①当y=1时,☉P与x轴相切,此时-x2-4x-3=1,解得x1=x2=-2,∴P1(-2,1);②当y=-1时,☉P与x轴相切,此时-x2-4x-3=-1,解得x=-2±,
∴P2(-2-,-1),P3(-2+,-1).故点P的坐标为(-2,1),(-2-,-1)或(-2+,-1).
15.【参考答案】(1)点D的位置如图所示.点D的坐标为(2,-2).
(4分)
(2)如图,易得☉D的半径为=2.
连接AC,则AC==2.
∵(2)2+(2)2=(2)2,
∴△ACD是等腰直角三角形,且∠ADC=90°. (6分)
∴弧AC的长为=π. (8分)
16.【参考答案】如图,连接OC,OD.
∵五边形ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
∴∠CPD的余角的度数为90°-36°=54°. (8分)
17.【参考答案】如图,连接OC. (1分)
∵CD⊥AB,AB为☉O的直径,CD=10寸,
∴CE=DE=CD=5寸. (4分)
设OC=OA=x寸,则OE=(x-1)寸.
由勾股定理,得OE2+CE2=OC2,
即(x-1)2+52=x2,
解得x=13,
∴AB=26寸, (7分)
故直径AB的长为26寸. (8分)
18.【参考答案】∵∠ACB=∠DEC=90°,∠A=45°,∠D=30°,
∴∠DCE=60°,∠B=45°. (2分)
由旋转可得∠D'CE'=∠DCE=60°,∠BCE'=15°,D'C=DC=7,
∴∠OCB=45°, (4分)
∴∠COB=180°-45°-45°=90°,
∴∠AOD'=90°.
又∠CAB=45°,∠ACB=90°,
∴AO=CO=BO=AB=3,
∴D'O=D'C-CO=4,
∴AD'==5. (8分)
19.【参考答案】(1)DE所在直线与☉O相切.
理由:如图,连接BD,
∵∠BAD=90°,
∴BD为☉O的直径.
∴∠DCE=∠DCB=90°,
∴∠E+∠CDE=90°. (2分)
∵∠E=∠BAC,∠BDC=∠BAC,
∴∠E=∠BDC,
∴∠BDE=∠BDC+∠CDE=∠E+∠CDE=90°.
∴DE所在直线与☉O相切. (5分)
(2)如图,连接OC,
∵∠CDE=25°,
∴∠BDC=90°-25°=65°,
∴∠BOC=2∠BDC=2×65°=130°,
∴的长==π. (10分)
(第19题) (第20题)
20.【参考答案】(1)△ABC是等边三角形. (1分)
理由:如图,连接CD.
∵AC为☉O的直径,
∴CD⊥AB.
∵AD=BD,
∴易证得AC=BC.
∵∠ADE=120°,
∴∠ACE=60°,
∴△ABC是等边三角形. (5分)
(2)∵∠ADE=120°,∠CAB=60°,
∴DE∥AC,
∴△BDE是等边三角形. (6分)
∵AD=BD,
∴DE=AD,
∴=,
∴S弓形DE=S弓形AD,
∴S阴影=S△DEB. (8分)
∵AC=2,
∴BD=1,
∴S阴影=S△DEB=. (10分)
21.【参考答案】(1)如图,连接OB.
∵AB与☉O相切于点B,
∴OB⊥AB.
∵sin A=,
∴∠A=30°,
∴∠AOB=60°,
∴∠BOD=120°.
∵点E在上,
∴∠BED=∠BOD=60°. (6分)
(2)证明:如图,连接OF.
由(1)得OB⊥AB,∠BOD=120°.
∵OB=3,BF=3,
∴tan∠BOF==,
∴∠BOF=60°,
∴∠DOF=60°. (9分)
在△BOF与△DOF中,
∴△BOF≌△DOF,
∴∠ODF=∠OBF=90°.
又点D在☉O上,
∴DF与☉O相切. (12分)
22.【参考答案】(1)∵△OPC的边OC的长是定值,
∴当OP⊥OC时,OC边上的高最大,此时△OPC的面积最大.
∵AB=4,BC=2,
∴OP=OB=2,OC=OB+BC=4,
∴S△OPC=OC·OP=×4×2=4,
即△OPC的最大面积为4. (4分)
(2)当PC与☉O相切,即OP⊥PC时,∠OCP的度数最大.
在Rt△OPC中,∠OPC=90°,OC=4,OP=2,
∴sin∠OCP==,
∴∠OCP=30°,即∠OCP的最大度数为30°. (7分)
(3)证明:如图,连接AP,BP.
∵∠AOP=∠DOB,
∴AP=DB.
∵CP=DB,
∴AP=PC,
∴∠PAC=∠C.
∵AB=4,
∴OB=2,
∴OC=4,
∴△PAB≌△PCO,
∴∠BPA=∠OPC.
∵AB是☉O的直径,
∴∠BPA=90°,
∴∠OPC=90°,
∴CP是☉O的切线. (12分)
23.【参考答案】【问题呈现】在△MBA和△MGC中,
∴△MBA≌△MGC,
∴MB=MG. (4分)
∵MD⊥BC,
∴BD=GD,
∴DC=GC+GD=AB+BD. (6分)
【实践应用】(1)BE=CE+AC. (8分)
(2)∵AB=AC,
=,
∴A是的中点.
由AE⊥CD,根据阿基米德折弦定理,
得CE=BD+DE. (10分)
∵△BCD的周长为4+2,
∴BD+CD+BC=4+2,
∴BD+DE+CE+BC=2CE+BC=4+2. (12分)
∵BC=2,
∴CE=2.
在Rt△ACE中,∠ACD=45°,
∴AE=CE=2,
∴AC==4. (14分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024沪科版九年级数学下学期单元测试卷
第24章 圆
时间:120分钟 满分:150分
题号 一 二 三 四 五 六 七 八 评价
错题
一、选择题(本大题共10小题,每小题4分,满分40分.每小题有四个选项,其中只有一个选项符合题意)
1.中华文化博大精深,以下是“育”“才”“水”“井”四字的甲骨文,其中是中心对称、但非轴对称图形的是 ( )
A B C D
2.(2022·河南漯河期中)如图,将△ABC绕点A逆时针旋转100°得到△ADE,若点D在线段BC的延长线上,则∠ADE= ( )
A.60° B.50° C.45° D.40°
(第2题) (第3题)
3.(2021·福建福州期中)如图,AB是☉O的直径,点C,D在☉O上,∠BDC=21°,则∠AOC= ( )
A.136° B.137° C.138° D.139°
4.(2021·江苏苏州期中)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是
A(-3,0),B(-1,2),C(3,2),则△ABC的外心的坐标是 ( )
A.(1,-2) B.(0,0) C.(1,-1) D.(0,-1)
(第4题) (第5题)
5.如图,四边形ABCD是☉O的内接四边形,若∠BAC=35°,∠CBD=70°,则∠BCD的度数为 ( )
A.70° B.75° C.80° D.85°
6.(2022·浙江金华期中改编)如图,☉O与正六边形OABCDE的边OA,OE分别交于点F,G,点M为劣弧FG的中点.连接FM,GM,若FM=2,则☉O的半径为 ( )
A.2 B. C.2 D.2
7.一个圆锥的侧面积恰好等于其底面积的2倍,则该圆锥的侧面展开图所对应扇形的圆心角的度数为 ( )
A.180° B.90° C.120° D.60°
8.如图,已知点O是△ABC的内切圆的圆心,若∠BOC=124°,则∠A= ( )
A.56° B.60° C.62° D.68°
9.(2021·河南焦作期末)如图,四边形ABCD内接于☉O,AD∥BC,直线EF是☉O的切线,B是切点.若∠C=80°,∠ADB=54°,则∠CBF= ( )
A.45° B.46° C.54° D.60°
(第9题) (第10题)
10.如图,MN是☉O的直径,=,点B是劣弧AN的中点,点P是直径MN上一动点.连接AB,若MN=2,AB=-1,则△PAB的周长的最小值是 ( )
A.+1 B.+3 C.2 D.4
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(2022·广东广州海珠区期中改编)如图,E是正方形ABCD的边BC上一点,则△ABE绕点 逆时针至少旋转 后能够与△ADF重合.
(第11题) (第12题)
12.(2022·北京东城区期中)如图,AB是☉O的直径,AC是☉O的切线,A为切点,BC与☉O交于点D,连接OD.若∠C=50°,则∠AOD的度数为 .
13.(2022·江苏盐城景山中学月考)如图,正方形ABCD的边长为2,O为对角线的交点,点E,F分别为BC,AD的中点.以C为圆心,2为半径作,再分别以E,F为圆心,1为半径作,,则图中阴影部分的面积为 .(结果保留π)
(第13题) (第14题)
14.(2022·河北唐山丰南区联考改编)如图,P是抛物线y=-x2-4x-3上的一点,以点P为圆心、1个单位长度为半径作☉P,当☉P与x轴相切时,点P的坐标为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12.
13. 14.
三、(本大题共2小题,每小题8分,满分16分)
15.(2022·湖南长沙期末改编)如图,在正方形网格图中建立一个平面直角坐标系,一条圆弧经过网格点A(0,2),B(4,2),C(6,0).
(1)请在图中标出该圆弧所在圆的圆心D的位置并写出其坐标;
(2)连接AD,CD,求弧AC的长.(结果保留π)
16.(2021·安徽六安期末)如图,正五边形ABCDE内接于☉O,P为上的一点(点P不与点D,E重合),求∠CPD的余角的度数.
四、(本大题共2小题,每小题8分,满分16分)
17.在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何 ”用现代语言表述为:如图,AB为☉O的直径,弦CD⊥AB于点E,AE=1寸,CD=10寸,求直径AB的长.请你解答这个问题.
18.(2022·北京市师达中学月考)把一副三角板按如图(1)的方式摆放,其中∠ACB=
∠DEC=90°,∠A=45°,∠D=30°,AB=6,DC=7.如图(2),把三角板DCE绕点C顺时针旋转15°得到△D'CE',AB与CD'交于点O,D'E'与AB交于点F.连接AD',求线段AD'的长.
图(1) 图(2)
五、(本大题共2小题,每小题10分,满分20分)
19.(2021·吉林长春宽城区期末)如图,四边形ABCD内接于☉O,∠BAD=90°,AC为对角线,点E在BC的延长线上,且∠E=∠BAC.
(1)判断DE所在直线与☉O的位置关系,并说明理由.
(2)若∠CDE=25°,☉O的半径为3,求的长.(结果保留π)
20.如图,在△ABC中,以AC为直径的☉O分别交AB,BC于点D,E,连接DE,AD=BD,∠ADE=120°.
(1)试判断△ABC的形状并说明理由;
(2)若AC=2,求图中两个阴影部分的面积和.
六、(本题满分12分)
21.如图,AB与☉O相切于点B,AO交☉O于点C,AO的延长线交☉O于点D,E是上不与B,D重合的点,sin A=.
(1)求∠BED的大小;
(2)若☉O的半径为3,点F在AB的延长线上,且BF=3,求证:DF与☉O相切.
七、(本题满分12分)
22.如图(1),AB是☉O的直径,点C在AB的延长线上,AB=4,BC=2,P是☉O上半部分的一个动点,连接OP,CP.
(1)求△OPC的最大面积;
(2)求∠OCP的最大度数;
(3)如图(2),延长PO交☉O于点D,连接DB.当CP=DB时,求证:CP是☉O的切线.
图(1) 图(2)
八、(本题满分14分)
23.【问题呈现】阿基米德折弦定理:如图(1),AB和BC是☉O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是的中点,则从点M向BC作垂线,垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的部分证明过程.
图(1) 图(2) 图(3) 图(4)
证明:如图(2),在CB上截取CG=AB,连接MA,MB,MC,MG.
∵M是的中点,∴=,∴MA=MC.
……
请按照上面的证明思路,写出该证明的剩余部分.
【实践应用】
(1)如图(3),已知△ABC内接于☉O,BC>AB>AC,D是的中点,请你依据阿基米德折弦定理直接写出图中某三条线段之间的数量关系;
(2)如图(4),已知等腰三角形ABC内接于☉O,AB=AC,D为上一点,连接DB,DC,∠ACD=45°,AE⊥CD于点E,△BDC的周长为4+2,BC=2,请求出AC的长.
第24章 圆
1 2 3 4 5 6 7 8 9 10
C D C A B C A D B A
11.A 90° 12.80°
13.π-2 14.(-2,1),(-2-,-1)或(-2+,-1)
1.C
2.D 连接CD,因为点D在线段BC的延长线上,所以点B,C,D共线.根据旋转可知,AB=AD,
∠B=∠ADE,∠BAD=100°,∴∠B=∠ADB=×(180°-100°)=40°,∴∠ADE=∠B=40°.
3.C ∵∠BOC=2∠BDC,∠BDC=21°,∴∠BOC=42°,∴∠AOC=180°-42°=138°.
4.A ∵三角形的外心到三角形三个顶点的距离相等,∴线段BC,AB的垂直平分线的交点即为外心P,由图可知,点P的坐标为(1,-2).
5.B 由圆周角定理得∠CAD=∠CBD=70°,∴∠BAD=70°+35°=105°.∵四边形ABCD是☉O的内接四边形,∴∠BCD=180°-∠BAD=75°.
6.C 如图,连接OM,由题意知∠FOG=120°.∵点M为劣弧FG的中点,∴∠FOM=60°,OM=OF,∴△OFM是等边三角形,∴OM=OF=FM=2,则☉O的半径为2,故选C.
7.A 设该圆锥的母线长为R,圆锥的侧面展开图所对应扇形的圆心角的度数为n°,底面圆的半径为r,则底面圆的周长为2πr,底面圆的面积为πr2,该扇形的侧面积为×2πr×R=πRr.已知πRr=2×πr2,所以R=2r.因为扇形弧长=底面圆周长,所以=2πr, 解得n=180.
8.D ∵∠BOC=124°,∴∠OBC+∠OCB=180°-124°=56°.∵点O是△ABC的内切圆的圆心,∴OB,OC分别平分∠ABC和∠ACB,∴∠ABC=2∠OBC,∠ACB=2∠OCB,∴∠ABC+∠ACB=2(∠OBC+∠OCB)=112°,∴∠A=
180°-112°=68°.
9.B 如图,连接OD,OB,则∠BOD=2∠C=160°.∵OB=OD,∴∠OBD==10°.∵四边形ABCD内接于☉O,∴∠A=180°-∠C=100°.∵AD∥BC,∴∠DBC=∠ADB=54°,∴∠OBC=54°-10°=44°.∵EF是☉O的切线,
∴∠OBF=90°,∴∠CBF=90°-∠OBC=90°-44°=46°.故选B.
(第9题) (第10题)
10.A (将军饮马模型)如图,作点A关于MN的对称点A',连接A'B,交MN于点P,连接OA',OA,OB,PA.
∵点A与点A'关于MN对称,∴PA=PA'.由题意知∠A'ON=∠AON=60°.∵点B是劣弧AN的中点,
∴∠BON=30°,∴∠A'OB=∠A'ON+∠BON=90°.又OA=OA'=MN=,∴A'B=2,∴PA+PB=PA'+
PB=A'B=2.∵AB=-1,∴△PAB的周长的最小值是2+-1=+1.故选A.
11.A 90°
12.80° 由题意知∠CAB=90°.∵∠C=50°,∴∠ABC=90°-50°=40°.又OB=OD,∴∠ODB=∠OBD=40°,
∴∠AOD=∠OBD+∠ODB=40°+40°=80°.
13.π-2 (转化思想)连接BD,将不规则的阴影图形通过割补法转换成弓形BD,由题意知,阴影部分的面
积=S扇形CBD-S△BCD=π×22-×2×2=π-2.
14.(-2,1),(-2-,-1)或(-2+,-1) (分类讨论思想)如图,分两种情况讨论.①当y=1时,☉P与x轴相切,此时-x2-4x-3=1,解得x1=x2=-2,∴P1(-2,1);②当y=-1时,☉P与x轴相切,此时-x2-4x-3=-1,解得x=-2±,
∴P2(-2-,-1),P3(-2+,-1).故点P的坐标为(-2,1),(-2-,-1)或(-2+,-1).
15.【参考答案】(1)点D的位置如图所示.点D的坐标为(2,-2).
(4分)
(2)如图,易得☉D的半径为=2.
连接AC,则AC==2.
∵(2)2+(2)2=(2)2,
∴△ACD是等腰直角三角形,且∠ADC=90°. (6分)
∴弧AC的长为=π. (8分)
16.【参考答案】如图,连接OC,OD.
∵五边形ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
∴∠CPD的余角的度数为90°-36°=54°. (8分)
17.【参考答案】如图,连接OC. (1分)
∵CD⊥AB,AB为☉O的直径,CD=10寸,
∴CE=DE=CD=5寸. (4分)
设OC=OA=x寸,则OE=(x-1)寸.
由勾股定理,得OE2+CE2=OC2,
即(x-1)2+52=x2,
解得x=13,
∴AB=26寸, (7分)
故直径AB的长为26寸. (8分)
18.【参考答案】∵∠ACB=∠DEC=90°,∠A=45°,∠D=30°,
∴∠DCE=60°,∠B=45°. (2分)
由旋转可得∠D'CE'=∠DCE=60°,∠BCE'=15°,D'C=DC=7,
∴∠OCB=45°, (4分)
∴∠COB=180°-45°-45°=90°,
∴∠AOD'=90°.
又∠CAB=45°,∠ACB=90°,
∴AO=CO=BO=AB=3,
∴D'O=D'C-CO=4,
∴AD'==5. (8分)
19.【参考答案】(1)DE所在直线与☉O相切.
理由:如图,连接BD,
∵∠BAD=90°,
∴BD为☉O的直径.
∴∠DCE=∠DCB=90°,
∴∠E+∠CDE=90°. (2分)
∵∠E=∠BAC,∠BDC=∠BAC,
∴∠E=∠BDC,
∴∠BDE=∠BDC+∠CDE=∠E+∠CDE=90°.
∴DE所在直线与☉O相切. (5分)
(2)如图,连接OC,
∵∠CDE=25°,
∴∠BDC=90°-25°=65°,
∴∠BOC=2∠BDC=2×65°=130°,
∴的长==π. (10分)
(第19题) (第20题)
20.【参考答案】(1)△ABC是等边三角形. (1分)
理由:如图,连接CD.
∵AC为☉O的直径,
∴CD⊥AB.
∵AD=BD,
∴易证得AC=BC.
∵∠ADE=120°,
∴∠ACE=60°,
∴△ABC是等边三角形. (5分)
(2)∵∠ADE=120°,∠CAB=60°,
∴DE∥AC,
∴△BDE是等边三角形. (6分)
∵AD=BD,
∴DE=AD,
∴=,
∴S弓形DE=S弓形AD,
∴S阴影=S△DEB. (8分)
∵AC=2,
∴BD=1,
∴S阴影=S△DEB=. (10分)
21.【参考答案】(1)如图,连接OB.
∵AB与☉O相切于点B,
∴OB⊥AB.
∵sin A=,
∴∠A=30°,
∴∠AOB=60°,
∴∠BOD=120°.
∵点E在上,
∴∠BED=∠BOD=60°. (6分)
(2)证明:如图,连接OF.
由(1)得OB⊥AB,∠BOD=120°.
∵OB=3,BF=3,
∴tan∠BOF==,
∴∠BOF=60°,
∴∠DOF=60°. (9分)
在△BOF与△DOF中,
∴△BOF≌△DOF,
∴∠ODF=∠OBF=90°.
又点D在☉O上,
∴DF与☉O相切. (12分)
22.【参考答案】(1)∵△OPC的边OC的长是定值,
∴当OP⊥OC时,OC边上的高最大,此时△OPC的面积最大.
∵AB=4,BC=2,
∴OP=OB=2,OC=OB+BC=4,
∴S△OPC=OC·OP=×4×2=4,
即△OPC的最大面积为4. (4分)
(2)当PC与☉O相切,即OP⊥PC时,∠OCP的度数最大.
在Rt△OPC中,∠OPC=90°,OC=4,OP=2,
∴sin∠OCP==,
∴∠OCP=30°,即∠OCP的最大度数为30°. (7分)
(3)证明:如图,连接AP,BP.
∵∠AOP=∠DOB,
∴AP=DB.
∵CP=DB,
∴AP=PC,
∴∠PAC=∠C.
∵AB=4,
∴OB=2,
∴OC=4,
∴△PAB≌△PCO,
∴∠BPA=∠OPC.
∵AB是☉O的直径,
∴∠BPA=90°,
∴∠OPC=90°,
∴CP是☉O的切线. (12分)
23.【参考答案】【问题呈现】在△MBA和△MGC中,
∴△MBA≌△MGC,
∴MB=MG. (4分)
∵MD⊥BC,
∴BD=GD,
∴DC=GC+GD=AB+BD. (6分)
【实践应用】(1)BE=CE+AC. (8分)
(2)∵AB=AC,
=,
∴A是的中点.
由AE⊥CD,根据阿基米德折弦定理,
得CE=BD+DE. (10分)
∵△BCD的周长为4+2,
∴BD+CD+BC=4+2,
∴BD+DE+CE+BC=2CE+BC=4+2. (12分)
∵BC=2,
∴CE=2.
在Rt△ACE中,∠ACD=45°,
∴AE=CE=2,
∴AC==4. (14分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
