2024华师版九年级数学下学期单元测试卷--第26章二次函数测试卷(含答案)
文档属性
| 名称 | 2024华师版九年级数学下学期单元测试卷--第26章二次函数测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024华师版九年级数学下学期单元测试卷
第26章 二次函数
时间:90分钟 满分:100分
一、选择题(每小题3分,共30分)
1.用配方法将二次函数y=x2+8x-9化成顶点式的形式,下列正确的为 ( )
A.y=(x-4)2+7 B.y=(x-4)2-25 C.y=(x+4)2+7 D.y=(x+4)2-25
2.已知二次函数y=x2+bx+c(b,c均为常数)的图象经过点(-2,4),则b,c满足的
关系式是 ( )
A.c=2b B.b=2c C.b=-2c D.c=-2b
3.下列具有二次函数关系的是 ( )
A.正方形的周长C与边长x B.速度不变时,路程s与时间t
C.正方形的面积S与边长x D.三角形的高一定时,面积S与底边长x
4.已知二次函数y=ax2+bx+c,函数y与自变量x的部分对应值如下表,则方程ax2+bx+c=0的一个解x的范围是 ( )
x … 1 1.1 1.2 1.3 1.4 …
y … -1 -0.49 0.04 0.59 1.16 …
A.15.点A(m,n)在二次函数y=x2-4的图象上,则2m-n的最大值是 ( )
A.4 B.5 C.-4 D.-5
6.一枚炮弹发射后第x秒的高度为y米,且y与x之间的关系为y=ax2+bx+c(a≠0).若此炮弹发射后在第5秒与第7秒时的高度相等,则在下列时刻中炮弹所在高度最高的是 ( )
A.第5.1秒 B.第5.8秒 C.第5.9秒 D.第6.9秒
7.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的大致图象为 ( )
A B C D
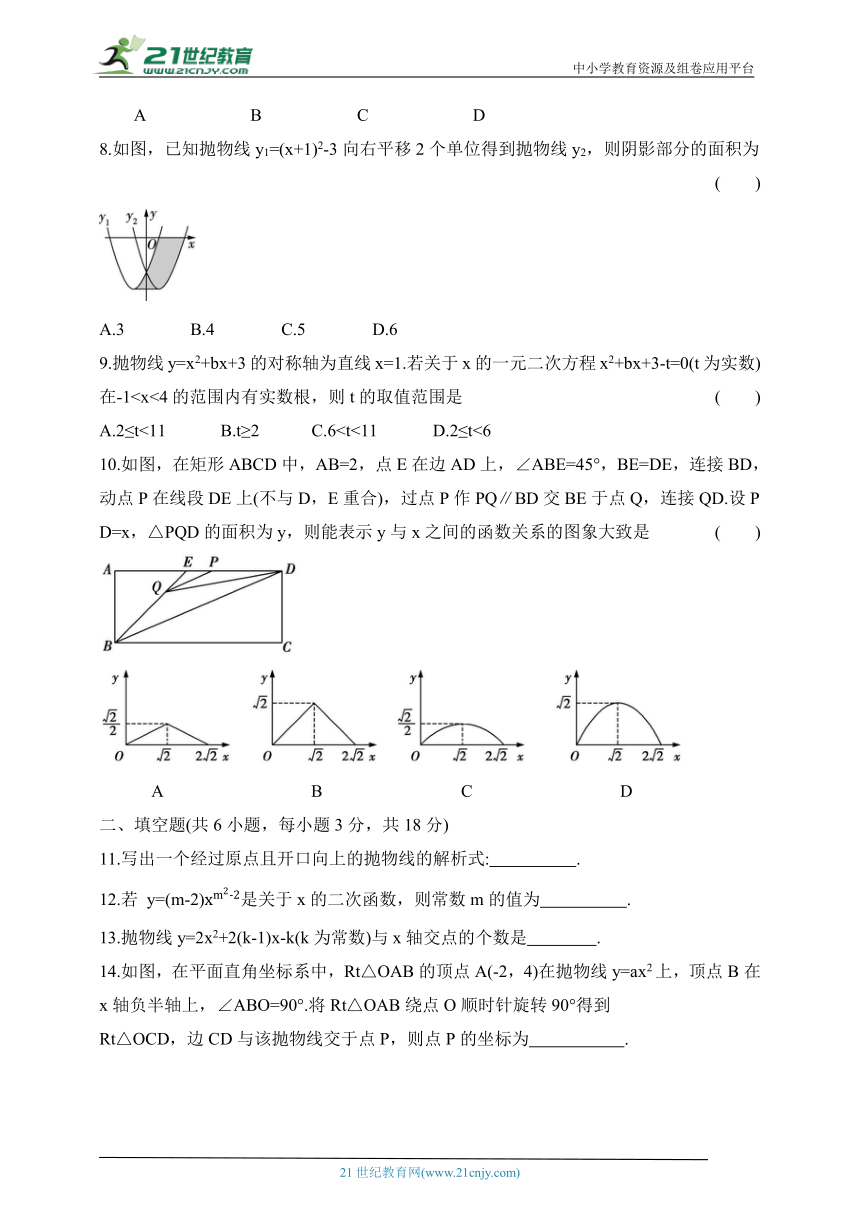
8.如图,已知抛物线y1=(x+1)2-3向右平移2个单位得到抛物线y2,则阴影部分的面积为 ( )
A.3 B.4 C.5 D.6
9.抛物线y=x2+bx+3的对称轴为直线x=1.若关于x的一元二次方程x2+bx+3-t=0(t为实数)在-1A.2≤t<11 B.t≥2 C.610.如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,动点P在线段DE上(不与D,E重合),过点P作PQ∥BD交BE于点Q,连接QD.设PD=x,△PQD的面积为y,则能表示y与x之间的函数关系的图象大致是 ( )
A B C D
二、填空题(共6小题,每小题3分,共18分)
11.写出一个经过原点且开口向上的抛物线的解析式: .
12.若 y=(m-2)是关于x的二次函数,则常数m的值为 .
13.抛物线y=2x2+2(k-1)x-k(k为常数)与x轴交点的个数是 .
14.如图,在平面直角坐标系中,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,顶点B在x轴负半轴上,∠ABO=90°.将Rt△OAB绕点O顺时针旋转90°得到
Rt△OCD,边CD与该抛物线交于点P,则点P的坐标为 .
15.某农场拟用围栏建两间如图所示的矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,所有围栏的总长(不含门)为26 m,若要使得建成的饲养室总面积最大,则利用墙体的长度为 m.
16.如图,二次函数y=ax2+bx+c(a≠0)的图象经过点A,B,C,现有下面四个推断:
①抛物线开口向下;②当x=-2时,y取最大值;③当m<4时,关于x的一元二次方程ax2+bx+c=m必有两个不相等的实数根;④直线y=kx+c(k≠0)经过点A,C,当
kx+c>ax2+bx+c时,x的取值范围是-4三、解答题(共6小题,共52分)
17.(6分)已知二次函数y=x2+2x+c的图象经过点(2,5).
(1)求该二次函数的表达式及其顶点坐标;
(2)若该抛物线向右平移1个单位长度、向上平移2个单位长度后得到新抛物线,判断点(-1,2)是否在新抛物线上.
18.(7分)如图,一个运动员推铅球,铅球在点A处出手,出手后的铅球沿一段抛物线运行,运行至点B处达到最高.已知铅球运行高度y(m)与水平距离x(m)之间的函数关系是y=-(x-4)2+3,按如图所示建立平面直角坐标系.请判断铅球推出的距离能否达到11 m,并说明理由.
19.(8分)小爱同学学习二次函数后,对函数y=-(|x|-1)2进行了探究.在经历列表、描点、连线步骤后,得到如下的函数图象.请根据函数图象,回答下列问题:
(1)观察探究:
①写出该函数的一条性质: ;
②方程-(|x|-1)2=-1的解为 ;
③若方程-(|x|-1)2=a有四个实数根,则a的取值范围是 .
(2)延伸思考:
将函数y=-(|x|-1)2的图象经过怎样的平移可得到函数y1=-(|x-2|-1)2+3的图象 写出平移过程,并直接写出当220.(9分)小李在某景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可销售200件.经市场调查发现,销售单价每提高1元,日销量将会减少10件,而物价部门规定,销售单价不能超过12元.设该纪念品的销售单价为x(元),日销量为y(件),日销售利润为w(元).
(1)求y与x之间的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元
(3)求日销售利润w(元)与销售单价x(元)之间的函数关系式,计算当x为何值时,日销售利润最大,求出最大利润.
21.(10分)在平面直角坐标系中,设二次函数y=-x2+ax+b(a,b为常数,b≠0).
(1)若该函数图象的对称轴为直线x=3,且图象经过点(0,2),求该函数的表达式;
(2)若r(r≠0)是关于x的方程bx2+ax-1=0的根,求证:二次函数y=-x2+ax+b的图象经过点(,0);
(3)若该二次函数的最大值为a,求b的取值范围.
22.(12分)如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点(点A在点B左侧),点B的坐标为(1,0),OC=3BO.
(1)求抛物线所对应的函数表达式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以点A,C,E,P为顶点且以AC为一边的平行四边形 若存在,求出点P的坐标;若不存在,请说明理由.
备用图
参考答案与解析
1.D y=x2+8x-9=x2+8x+16-9-16=(x+4) 2-25.
2.A 将(-2,4)代入y=x2+bx+c,得4=4-2b+c,∴c=2b.
3.C
4.B
5.B 把(m,n)代入y=x2-4,得n=m2-4,∴2m-n=2m-(m2-4)=-m2+2m+4=-(m-1)2
+5.∵-1<0,∴当m=1时,2m-n有最大值,最大值是5.
6.C 由题意得,抛物线y=ax2+bx+c(a<0)的对称轴为直线x==6.∵5.9最接近6,∴第5.9秒时,炮弹所在高度最高.
7.B ∵二次函数的图象开口向上,∴a>0.∵函数图象的对称轴在y轴右侧,∴x=
->0,∴b<0.∵二次函数的图象与y轴的正半轴相交,∴c>0.由a>0,b<0,c>0知y=ax+b的图象经过第一、三、四象限,反比例函数y=的图象位于第一、三象限,只有B选项中的图象符合.故选B.
8.D 如图,设点M为抛物线y1的顶点,点N为抛物线y2的顶点,连接MA,NB,则四边形AMNB的面积和阴影部分的面积相等.由题意得AB∥MN,AB=MN
=2,∴四边形AMNB是平行四边形.∵抛物线y1=(x+1)2-3,∴顶点M的坐标为(-1,-3),∴点M到x轴的距离为3,∴平行四边形AMNB的面积是2×3=6,∴阴影部分面积是6.
9.A 由题意可知-=1,解得b=-2,故该抛物线的解析式为y=x2-2x+3,抛物线如图所示.一元二次方程x2+bx+3-t=0在-1x2+bx+3与直线y=t在-110.C 过点Q作QF⊥AD于点F.在Rt△ABE中,∵∠ABE=45°,∴BE=AB
=2,∴DE=BE=2.∵PQ∥BD,∴∠EPQ=∠EDB,∠EQP=∠EBD.∵BE=DE,∴∠EDB=∠EBD,∴∠EPQ=∠EQP,∴QE=PE=2-x.在Rt△EQF中,∠FEQ=
45°,∴QF=EQ=2-x,∴y=x(2-x)=x-x2(011.y=x2+x(答案不唯一) 设抛物线的解析式为y=ax2+bx+c,∵抛物线开口向上,∴a>0.∵抛物线过原点,∴c=0.∵对称轴没有限制,∴b可取任意值,故该抛物线的解析式满足y=ax2+bx(a>0)即可.
12.-2 ∵y=(m-2)是关于x的二次函数,∴解得m=-2.
13.2 对于y=2x2+2(k-1)x-k,令y=0,则2x2+2(k-1)x-k=0,Δ=b2-4ac=4(k-1)2-4×2×
(-k)=4k2+4>0,∴该抛物线与x轴的交点个数是2.
14.(,2) ∵点A(-2,4)在抛物线y=ax2上,∴4=a×(-2)2,解得a=1,∴抛物线的解析式为y=x2.∵Rt△OAB绕点O顺时针旋转90°得到Rt△OCD,∴OB=OD=2,CD∥x轴,∴yp=2,∴令y=2,得2=x2,解得x=±.∵点P在第一象限,∴点P的坐标为(,2).
15.14 设利用墙体的长度为x m,则垂直于墙体的围栏长为(28-x)m,则饲养室总面积S=x(28-x)=-(x-14)2+,所以要使得建成的饲养室总面积最大,利用墙体的长度为14 m.
16.2 由题图可得抛物线开口向下,∴①正确;∵点A(-4,2),C(0,3)不关于直线x=-2对称,∴当x=-2时,y不取最大值,∴②错误;∵抛物线开口向下,且经过(-2,4),∴当m<4时,ax2+bx+c=m必有两个不相等的实数根,∴③正确;∵直线y=kx+c(k≠0)经过点A,C,即抛物线与直线相交于点A,C,且抛物线开口向下,∴当-417.【参考答案】(1)∵点(2,5)在二次函数y=x2+2x+c的图象上,
∴4+4+c=5,解得c=-3,∴该二次函数的表达式为y=x2+2x-3.
∵y=x2+2x-3=(x+1)2-4,∴该二次函数的顶点坐标为(-1,-4). (3分)
(2)将该抛物线向右平移1个单位长度、向上平移2个单位长度后得到的新抛物线为y=x2-2,把x=-1代入,得y=-1,∴点(-1,2)不在新抛物线上. (6分)
18.【参考答案】不能.理由如下: (1分)
令y=0,则-(x-4)2+3=0,即(x-4)2=36,解得x1=10,x2=-2(舍去). (5分)
∵10<11, (6分)
∴铅球推出的距离不能达到11 m. (7分)
19.【参考答案】(1)①图象关于y轴对称[当x=-1或x=1时,y取最大值,最大值为0;当x<-1或01或-1②x1=-2, x2=0,x3=2 (5分)
③-1(2)将函数y的图象先向右平移2个单位长度,再向上平移3个单位长度(或先向上平移3个单位长度,再向右平移2个单位长度)得到函数y1的图象. (7分)
当220.【参考答案】(1)根据题意,得y=200-10(x-8)=-10x+280,
故y=-10x+280. (2分)
(2)根据题意,得(x-6)(-10x+280)=720,解得x1=10,x2=24(舍去). (4分)
答:要使日销售利润为720元,销售单价应定为10元. (5分)
(3)根据题意,得w=(x-6)(-10x+280)=-10(x-17)2+1 210.
∵-10<0,∴当x<17时,w随x的增大而增大,
∴当x=12时,w最大,最大利润为960元.
答:当x为12时,日销售利润最大,最大利润为960元. (9分)
21.【参考答案】(1)∵函数图象的对称轴为直线x=3,∴=3,∴a=6.
∵图象经过点(0,2),∴b=2,∴函数的表达式为y=-x2+6x+2. (3分)
(2)证明:∵r(r≠0)是关于x的方程bx2+ax-1=0的根,∴br2+ar-1=0. (4分)
对于y=-x2+ax+b,当x=时,y=-()2+a×+b==0,
∴二次函数y=-x2+ax+b的图象经过点(,0). (6分)
(3)∵y=-x2+ax+b的二次项系数为负数,
∴y=-x2+ax+b的图象开口向下,∴y最大值===a, (7分)
化简得,b=-a2+a=-(a-2)2+1. (8分)
∵(a-2)2≥0,∴-(a-2)2≤0,∴-(a-2)2+1≤1,∴b的取值范围为b≤1. (10分)
22.【参考答案】(1)∵B(1,0),∴OB=1.
∵OC=3BO,∴OC=3,即C(0,-3). (1分)
∵抛物线y=ax2+3ax+c经过点B(1,0),C(0,-3),∴解得
故抛物线所对应的函数表达式为y=x2+x-3. (3分)
(2)如图1,过点D作DN∥y轴,分别交线段AC和x轴于点M,N.
图1 图2
对于y=x2+x-3,令y=0,得x2+x-3=0,解得x1=-4,x2=1,∴A(-4,0).
设直线AC的表达式为y=kx+b,则解得
故直线AC的表达式为y=-x-3. (5分)
S四边形ABCD=S△ABC+S△ADC=×5×3+DM·(AN+ON)=+2DM.
设D(x,x2+x-3),M(x,-x-3),则DM=-x-3-(x2+x-3)=-(x+2)2+3.(6分)
当x=-2时,DM有最大值3,
此时四边形ABCD的面积最大,最大值为+2×3=. (7分)
(3)如图2,①当AE为边时,四边形ACP1E1为平行四边形.∵C(0,-3),∴可设P1(n,-3),∴n2+n-3=-3,解得n1=0(舍去),n2=-3,∴P1(-3,-3). (9分)
②当AE为对角线时,四边形ACE2P2,ACE3P3为平行四边形.
∵C(0,-3),∴可设P(m,3),∴m2+m-3=3,解得m=或m=,
此时P2(,3),P3(,3).
综上,点P的坐标为(-3,-3),(,3)或(,3). (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华师版九年级数学下学期单元测试卷
第26章 二次函数
时间:90分钟 满分:100分
一、选择题(每小题3分,共30分)
1.用配方法将二次函数y=x2+8x-9化成顶点式的形式,下列正确的为 ( )
A.y=(x-4)2+7 B.y=(x-4)2-25 C.y=(x+4)2+7 D.y=(x+4)2-25
2.已知二次函数y=x2+bx+c(b,c均为常数)的图象经过点(-2,4),则b,c满足的
关系式是 ( )
A.c=2b B.b=2c C.b=-2c D.c=-2b
3.下列具有二次函数关系的是 ( )
A.正方形的周长C与边长x B.速度不变时,路程s与时间t
C.正方形的面积S与边长x D.三角形的高一定时,面积S与底边长x
4.已知二次函数y=ax2+bx+c,函数y与自变量x的部分对应值如下表,则方程ax2+bx+c=0的一个解x的范围是 ( )
x … 1 1.1 1.2 1.3 1.4 …
y … -1 -0.49 0.04 0.59 1.16 …
A.1
A.4 B.5 C.-4 D.-5
6.一枚炮弹发射后第x秒的高度为y米,且y与x之间的关系为y=ax2+bx+c(a≠0).若此炮弹发射后在第5秒与第7秒时的高度相等,则在下列时刻中炮弹所在高度最高的是 ( )
A.第5.1秒 B.第5.8秒 C.第5.9秒 D.第6.9秒
7.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的大致图象为 ( )
A B C D
8.如图,已知抛物线y1=(x+1)2-3向右平移2个单位得到抛物线y2,则阴影部分的面积为 ( )
A.3 B.4 C.5 D.6
9.抛物线y=x2+bx+3的对称轴为直线x=1.若关于x的一元二次方程x2+bx+3-t=0(t为实数)在-1
A B C D
二、填空题(共6小题,每小题3分,共18分)
11.写出一个经过原点且开口向上的抛物线的解析式: .
12.若 y=(m-2)是关于x的二次函数,则常数m的值为 .
13.抛物线y=2x2+2(k-1)x-k(k为常数)与x轴交点的个数是 .
14.如图,在平面直角坐标系中,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,顶点B在x轴负半轴上,∠ABO=90°.将Rt△OAB绕点O顺时针旋转90°得到
Rt△OCD,边CD与该抛物线交于点P,则点P的坐标为 .
15.某农场拟用围栏建两间如图所示的矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,所有围栏的总长(不含门)为26 m,若要使得建成的饲养室总面积最大,则利用墙体的长度为 m.
16.如图,二次函数y=ax2+bx+c(a≠0)的图象经过点A,B,C,现有下面四个推断:
①抛物线开口向下;②当x=-2时,y取最大值;③当m<4时,关于x的一元二次方程ax2+bx+c=m必有两个不相等的实数根;④直线y=kx+c(k≠0)经过点A,C,当
kx+c>ax2+bx+c时,x的取值范围是-4
17.(6分)已知二次函数y=x2+2x+c的图象经过点(2,5).
(1)求该二次函数的表达式及其顶点坐标;
(2)若该抛物线向右平移1个单位长度、向上平移2个单位长度后得到新抛物线,判断点(-1,2)是否在新抛物线上.
18.(7分)如图,一个运动员推铅球,铅球在点A处出手,出手后的铅球沿一段抛物线运行,运行至点B处达到最高.已知铅球运行高度y(m)与水平距离x(m)之间的函数关系是y=-(x-4)2+3,按如图所示建立平面直角坐标系.请判断铅球推出的距离能否达到11 m,并说明理由.
19.(8分)小爱同学学习二次函数后,对函数y=-(|x|-1)2进行了探究.在经历列表、描点、连线步骤后,得到如下的函数图象.请根据函数图象,回答下列问题:
(1)观察探究:
①写出该函数的一条性质: ;
②方程-(|x|-1)2=-1的解为 ;
③若方程-(|x|-1)2=a有四个实数根,则a的取值范围是 .
(2)延伸思考:
将函数y=-(|x|-1)2的图象经过怎样的平移可得到函数y1=-(|x-2|-1)2+3的图象 写出平移过程,并直接写出当2
(1)求y与x之间的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元
(3)求日销售利润w(元)与销售单价x(元)之间的函数关系式,计算当x为何值时,日销售利润最大,求出最大利润.
21.(10分)在平面直角坐标系中,设二次函数y=-x2+ax+b(a,b为常数,b≠0).
(1)若该函数图象的对称轴为直线x=3,且图象经过点(0,2),求该函数的表达式;
(2)若r(r≠0)是关于x的方程bx2+ax-1=0的根,求证:二次函数y=-x2+ax+b的图象经过点(,0);
(3)若该二次函数的最大值为a,求b的取值范围.
22.(12分)如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点(点A在点B左侧),点B的坐标为(1,0),OC=3BO.
(1)求抛物线所对应的函数表达式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以点A,C,E,P为顶点且以AC为一边的平行四边形 若存在,求出点P的坐标;若不存在,请说明理由.
备用图
参考答案与解析
1.D y=x2+8x-9=x2+8x+16-9-16=(x+4) 2-25.
2.A 将(-2,4)代入y=x2+bx+c,得4=4-2b+c,∴c=2b.
3.C
4.B
5.B 把(m,n)代入y=x2-4,得n=m2-4,∴2m-n=2m-(m2-4)=-m2+2m+4=-(m-1)2
+5.∵-1<0,∴当m=1时,2m-n有最大值,最大值是5.
6.C 由题意得,抛物线y=ax2+bx+c(a<0)的对称轴为直线x==6.∵5.9最接近6,∴第5.9秒时,炮弹所在高度最高.
7.B ∵二次函数的图象开口向上,∴a>0.∵函数图象的对称轴在y轴右侧,∴x=
->0,∴b<0.∵二次函数的图象与y轴的正半轴相交,∴c>0.由a>0,b<0,c>0知y=ax+b的图象经过第一、三、四象限,反比例函数y=的图象位于第一、三象限,只有B选项中的图象符合.故选B.
8.D 如图,设点M为抛物线y1的顶点,点N为抛物线y2的顶点,连接MA,NB,则四边形AMNB的面积和阴影部分的面积相等.由题意得AB∥MN,AB=MN
=2,∴四边形AMNB是平行四边形.∵抛物线y1=(x+1)2-3,∴顶点M的坐标为(-1,-3),∴点M到x轴的距离为3,∴平行四边形AMNB的面积是2×3=6,∴阴影部分面积是6.
9.A 由题意可知-=1,解得b=-2,故该抛物线的解析式为y=x2-2x+3,抛物线如图所示.一元二次方程x2+bx+3-t=0在-1
=2,∴DE=BE=2.∵PQ∥BD,∴∠EPQ=∠EDB,∠EQP=∠EBD.∵BE=DE,∴∠EDB=∠EBD,∴∠EPQ=∠EQP,∴QE=PE=2-x.在Rt△EQF中,∠FEQ=
45°,∴QF=EQ=2-x,∴y=x(2-x)=x-x2(0
12.-2 ∵y=(m-2)是关于x的二次函数,∴解得m=-2.
13.2 对于y=2x2+2(k-1)x-k,令y=0,则2x2+2(k-1)x-k=0,Δ=b2-4ac=4(k-1)2-4×2×
(-k)=4k2+4>0,∴该抛物线与x轴的交点个数是2.
14.(,2) ∵点A(-2,4)在抛物线y=ax2上,∴4=a×(-2)2,解得a=1,∴抛物线的解析式为y=x2.∵Rt△OAB绕点O顺时针旋转90°得到Rt△OCD,∴OB=OD=2,CD∥x轴,∴yp=2,∴令y=2,得2=x2,解得x=±.∵点P在第一象限,∴点P的坐标为(,2).
15.14 设利用墙体的长度为x m,则垂直于墙体的围栏长为(28-x)m,则饲养室总面积S=x(28-x)=-(x-14)2+,所以要使得建成的饲养室总面积最大,利用墙体的长度为14 m.
16.2 由题图可得抛物线开口向下,∴①正确;∵点A(-4,2),C(0,3)不关于直线x=-2对称,∴当x=-2时,y不取最大值,∴②错误;∵抛物线开口向下,且经过(-2,4),∴当m<4时,ax2+bx+c=m必有两个不相等的实数根,∴③正确;∵直线y=kx+c(k≠0)经过点A,C,即抛物线与直线相交于点A,C,且抛物线开口向下,∴当-4
∴4+4+c=5,解得c=-3,∴该二次函数的表达式为y=x2+2x-3.
∵y=x2+2x-3=(x+1)2-4,∴该二次函数的顶点坐标为(-1,-4). (3分)
(2)将该抛物线向右平移1个单位长度、向上平移2个单位长度后得到的新抛物线为y=x2-2,把x=-1代入,得y=-1,∴点(-1,2)不在新抛物线上. (6分)
18.【参考答案】不能.理由如下: (1分)
令y=0,则-(x-4)2+3=0,即(x-4)2=36,解得x1=10,x2=-2(舍去). (5分)
∵10<11, (6分)
∴铅球推出的距离不能达到11 m. (7分)
19.【参考答案】(1)①图象关于y轴对称[当x=-1或x=1时,y取最大值,最大值为0;当x<-1或0
③-1
当2
故y=-10x+280. (2分)
(2)根据题意,得(x-6)(-10x+280)=720,解得x1=10,x2=24(舍去). (4分)
答:要使日销售利润为720元,销售单价应定为10元. (5分)
(3)根据题意,得w=(x-6)(-10x+280)=-10(x-17)2+1 210.
∵-10<0,∴当x<17时,w随x的增大而增大,
∴当x=12时,w最大,最大利润为960元.
答:当x为12时,日销售利润最大,最大利润为960元. (9分)
21.【参考答案】(1)∵函数图象的对称轴为直线x=3,∴=3,∴a=6.
∵图象经过点(0,2),∴b=2,∴函数的表达式为y=-x2+6x+2. (3分)
(2)证明:∵r(r≠0)是关于x的方程bx2+ax-1=0的根,∴br2+ar-1=0. (4分)
对于y=-x2+ax+b,当x=时,y=-()2+a×+b==0,
∴二次函数y=-x2+ax+b的图象经过点(,0). (6分)
(3)∵y=-x2+ax+b的二次项系数为负数,
∴y=-x2+ax+b的图象开口向下,∴y最大值===a, (7分)
化简得,b=-a2+a=-(a-2)2+1. (8分)
∵(a-2)2≥0,∴-(a-2)2≤0,∴-(a-2)2+1≤1,∴b的取值范围为b≤1. (10分)
22.【参考答案】(1)∵B(1,0),∴OB=1.
∵OC=3BO,∴OC=3,即C(0,-3). (1分)
∵抛物线y=ax2+3ax+c经过点B(1,0),C(0,-3),∴解得
故抛物线所对应的函数表达式为y=x2+x-3. (3分)
(2)如图1,过点D作DN∥y轴,分别交线段AC和x轴于点M,N.
图1 图2
对于y=x2+x-3,令y=0,得x2+x-3=0,解得x1=-4,x2=1,∴A(-4,0).
设直线AC的表达式为y=kx+b,则解得
故直线AC的表达式为y=-x-3. (5分)
S四边形ABCD=S△ABC+S△ADC=×5×3+DM·(AN+ON)=+2DM.
设D(x,x2+x-3),M(x,-x-3),则DM=-x-3-(x2+x-3)=-(x+2)2+3.(6分)
当x=-2时,DM有最大值3,
此时四边形ABCD的面积最大,最大值为+2×3=. (7分)
(3)如图2,①当AE为边时,四边形ACP1E1为平行四边形.∵C(0,-3),∴可设P1(n,-3),∴n2+n-3=-3,解得n1=0(舍去),n2=-3,∴P1(-3,-3). (9分)
②当AE为对角线时,四边形ACE2P2,ACE3P3为平行四边形.
∵C(0,-3),∴可设P(m,3),∴m2+m-3=3,解得m=或m=,
此时P2(,3),P3(,3).
综上,点P的坐标为(-3,-3),(,3)或(,3). (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
