2024华师版九年级数学下学期单元测试卷--期末测试卷(含答案)
文档属性
| 名称 | 2024华师版九年级数学下学期单元测试卷--期末测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024华师版九年级数学下学期单元测试卷
期末测试卷
时间:100分钟 满分:120分
一、选择题(每小题3分,共30分)
1.二次函数y=-2(x+2)2的图象的顶点坐标是 ( )
A.(-2,0) B.(-2,2) C.(2,0) D.(2,-2)
2.下列计算正确的是 ( )
A.+= B.-8-=-7
C.×=4 D.=
3.下列说法,正确的是 ( )
A.“打开电视,正在播放中央电视台新闻”是必然事件
B.某种彩票中奖概率为10%是指买十张一定有一张中奖
C.神舟飞船发射前需要对零部件进行抽样调查
D.了解某种节能灯的使用寿命适合抽样调查
4.关于x的一元二次方程x2-3mx-13=0的根的情况是 ( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.没有实数根 D.无法确定
5.若关于x的二次函数y=ax2+bx+c的图象如图所示,则下列判断不正确的( )
A.a>0 B.abc<0 C.b>0 D.c>0
6.袋中有除颜色以外其余都相同的红球3个,黄球2个,摇匀后,从中任意摸出1个球,记录下颜色后放回、摇匀,再从中任意摸出1个球,像这样有放回地先后摸球3次,摸到的都是红球,则第4次摸到红球的概率是 ( )
A.1 B.0 C. D.
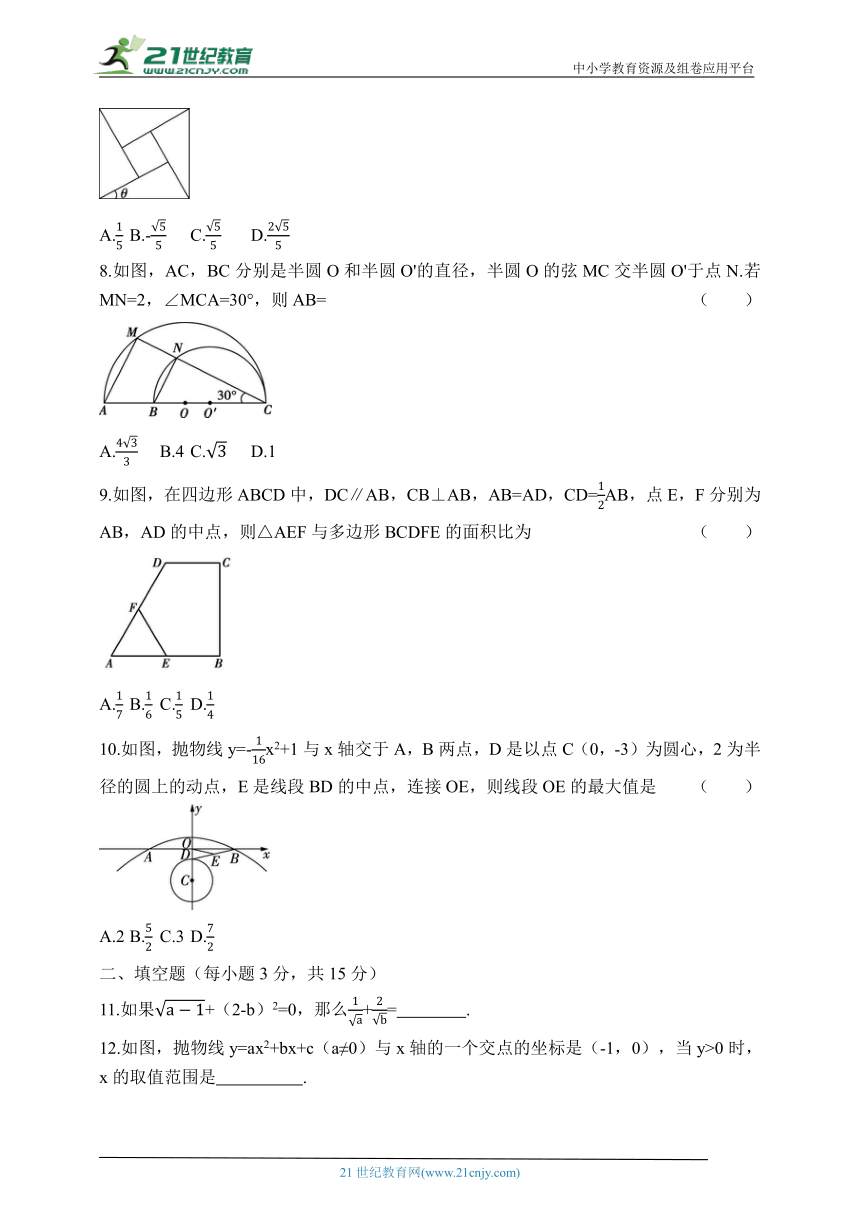
7.我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形组成的一个大正方形.如果大正方形的面积是100,小正方形的面积是20,那么sin θ-cos θ的值是 ( )
A. B.- C. D.
8.如图,AC,BC分别是半圆O和半圆O'的直径,半圆O的弦MC交半圆O'于点N.若MN=2,∠MCA=30°,则AB= ( )
A. B.4 C. D.1
9.如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,CD=AB,点E,F分别为AB,AD的中点,则△AEF与多边形BCDFE的面积比为 ( )
A. B. C. D.
10.如图,抛物线y=-x2+1与x轴交于A,B两点,D是以点C(0,-3)为圆心,2为半径的圆上的动点,E是线段BD的中点,连接OE,则线段OE的最大值是 ( )
A.2 B. C.3 D.
二、填空题(每小题3分,共15分)
11.如果+(2-b)2=0,那么+= .
12.如图,抛物线y=ax2+bx+c(a≠0)与x轴的一个交点的坐标是(-1,0),当y>0时,x的取值范围是 .
13.某校共有1 000名学生.为了解学生的中长跑成绩分布情况,随机抽取100名学生的中长跑成绩,画出条形统计图,如图.根据所学的统计知识可估计该校中长跑成绩优秀的学生人数是 .
14.我们知道,若抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,则一元二次方程ax2+bx+c=0有两个不相等的实数根.由此,若d,e(d15.如图,AB是半圆O的直径,AB=4,点C是半圆O上一点,且∠ABC=60°,∠ABC的平分线交半圆O于点D,点P是BD上一动点,点Q是AB上一动点,连接AP,PQ,则当AP+PQ的值最小时,图中阴影部分的面积为 .
三、解答题(共75分)
16.(7分)化简:|1-|+(2022-)0+-()-1+2 023(sin260°+cos260°).
17.(7分)如图,在5×5的方格纸中,已知格点三角形ABC,请按要求画图.
(1)在图1的方格纸中画一个格点三角形DEF,使△DEF∽△ABC,且△DEF
与△ABC 的周长比是2∶1.
(2)在图2的方格纸中画一个格点三角形MNL,使△MNL与△ABC相似,且△MNL与△ABC的面积比是2∶1.
图1 图2
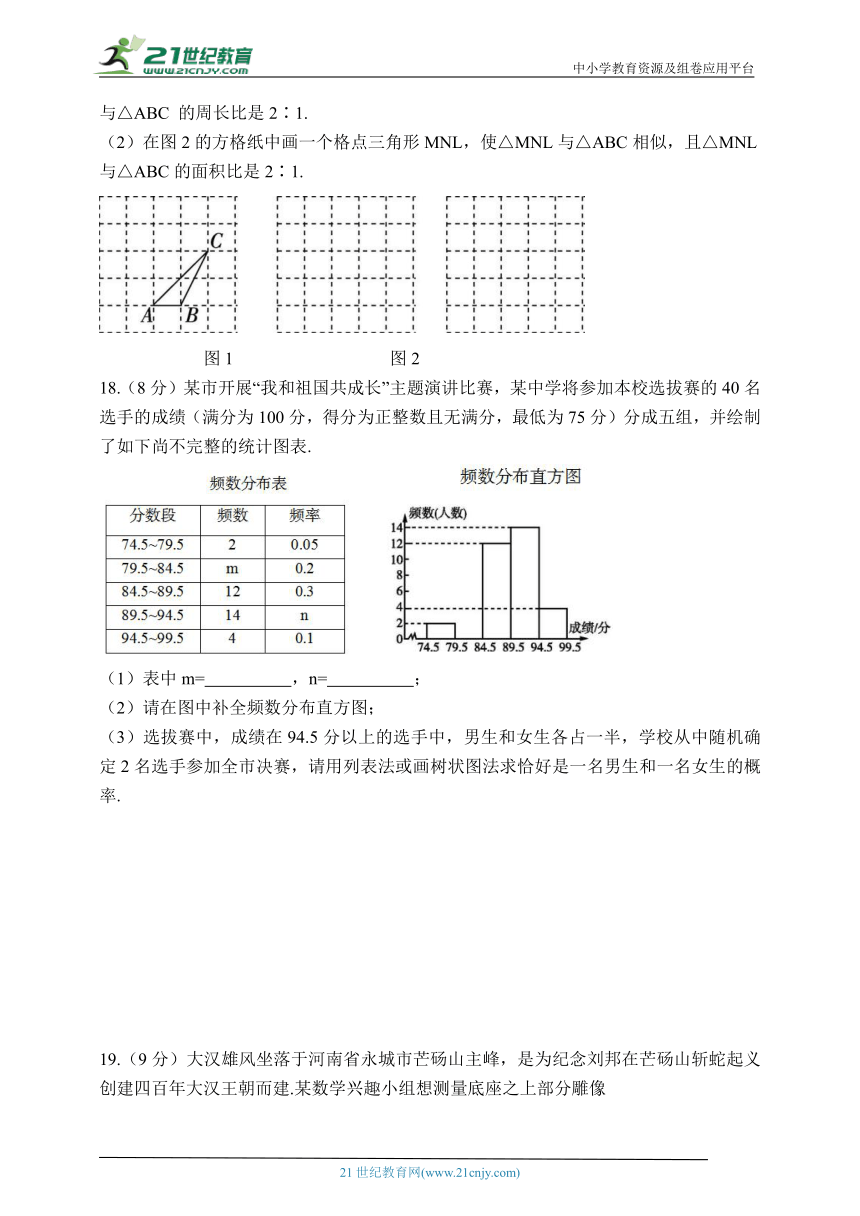
18.(8分)某市开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了如下尚不完整的统计图表.
(1)表中m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)选拔赛中,成绩在94.5分以上的选手中,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列表法或画树状图法求恰好是一名男生和一名女生的概率.
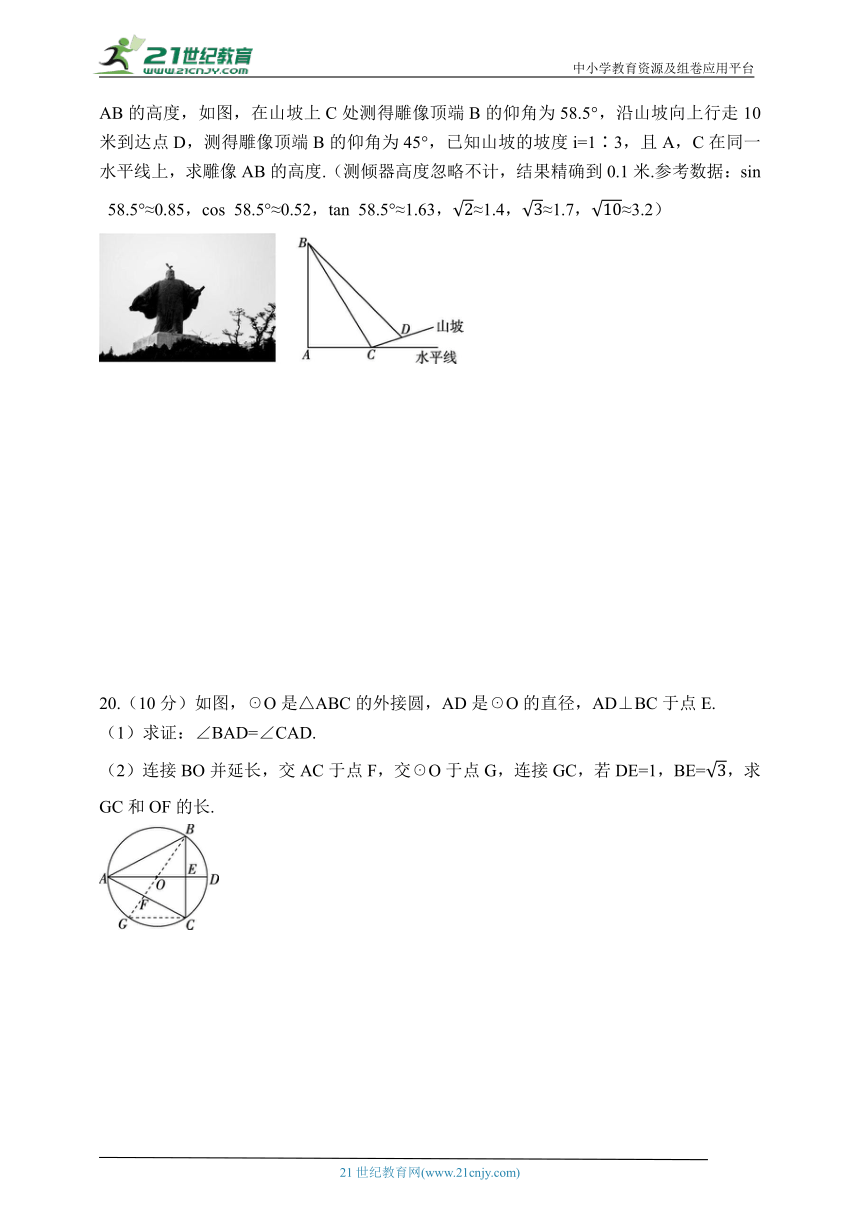
19.(9分)大汉雄风坐落于河南省永城市芒砀山主峰,是为纪念刘邦在芒砀山斩蛇起义创建四百年大汉王朝而建.某数学兴趣小组想测量底座之上部分雕像
AB的高度,如图,在山坡上C处测得雕像顶端B的仰角为58.5°,沿山坡向上行走10米到达点D,测得雕像顶端B的仰角为45°,已知山坡的坡度i=1∶3,且A,C在同一水平线上,求雕像AB的高度.(测倾器高度忽略不计,结果精确到0.1米.参考数据:sin 58.5°≈0.85,cos 58.5°≈0.52,tan 58.5°≈1.63,≈1.4,≈1.7,≈3.2)
20.(10分)如图,☉O是△ABC的外接圆,AD是☉O的直径,AD⊥BC于点E.
(1)求证:∠BAD=∠CAD.
(2)连接BO并延长,交AC于点F,交☉O于点G,连接GC,若DE=1,BE=,求GC和OF的长.
21.(11分)请阅读以下材料,并回答下列相应的问题.
角平分线分线段成比例定理的几何语言如下:如图1,在△ABC中,∵AD平分∠BAC,∴=.下面是这个定理的部分证明过程.
证明:如图2,过点C作CE∥DA,交BA的延长线于点E……
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知在Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,求△ABD的周长.
图1 图2 图3
22.(11分)定义:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的一半,则称这样的方程为“半根方程”.
(1)方程x2-5x+6=0 “半根方程”; (填“是”或“不是”)
(2)若关于x的方程(x-4)(mx+n)=0是“半根方程”,求的值;
(3)若关于x的方程x2+bx+c=0是“半根方程”,求证:2b2=9c.
23.(12分)如图1,在平面直角坐标系中,抛物线F1:y=a(x-)2+与x轴交于点A(-,0)和点B,与y轴交于点C.
(1)求抛物线F1的表达式.
(2)如图2,将抛物线F1先向左平移1个单位长度,再向下平移3个单位长度,得到抛物线F2,若抛物线F1与抛物线F2相交于点D,连接BD,CD,BC.
①求点D的坐标;
②判断△BCD的形状,并说明理由.
(3)在2的条件下,抛物线F2上是否存在点P,使得△BDP为等腰直角三角形 若存在,求出点P的坐标;若不存在,请说明理由.
图1 图2
参考答案与解析
1.A
2.C +=+2,-8-=-9,×==4,=.
3.D “打开电视,正在播放中央电视台新闻”是随机事件;某种彩票中奖概率为10%是指买十张可能中奖,也可能不中奖;神舟飞船发射前需要对零部件进行全面调查;了解某种节能灯的使用寿命,具有破坏性,适合抽样调查.故选D.
4.B 根据题意,得Δ=(-3m)2-4×1×(-13)=9m2+52.因为无论m为何值,9m2
≥0恒成立,所以9m2+52>0,所以一元二次方程x2-3mx-13=0有两个不相等的实数根.
5.B 因为抛物线开口向上,所以a>0.因为抛物线的对称轴在y轴左侧,所以
-<0,所以b>0.因为抛物线与y轴的正半轴相交,所以c>0,所以abc>0.
6.C 因为是有放回地摸球,所以每次红球被摸到的概率跟摸球的次数没有关系,所以在有3个红球,2个黄球的前提下,第4次摸到红球的概率是.
7.B ∵大正方形的面积是100,小正方形的面积是20,∴大正方形的边长为10,小正方形的边长为2,∴10cos θ-10sin θ=2,∴cos θ-sin θ=,∴sin θ -cos θ=-.
8.A ∵AC,BC分别是半圆O和半圆O'的直径,∴∠AMC=∠BNC=90°,∴
cos 30°===,∴CM=AC,CN=BC.∵MN=CM-CN=2,∴AC-BC=2,∴(AC-BC)×=2,即AB×=2,∴AB=.
9.C 如图,连接BD.∵F,E分别为AD,AB的中点,∴EF=BD,EF∥BD,∴△AEF∽△ABD,∴=()2=()2=,∴S△ABD=4S△AEF,∴S四边形BDFE=3S△AEF.∵====2,∴S△ABD=2S△BCD,∴S△BCD=2S△AEF,∴
==.
10.D 如图,连接AD,当y=0时,-x2+1=0,解得x1=4,x2=-4,∴A(-4,0),B(4,0).∵E是线段BD的中点,∴OE为△ABD的中位线,∴OE=
AD,即当AD最大时,OE最大,显然AD经过圆心C时,AD最大,即点D运动到点D'位置时,AD最大.∵AC==5,∴AD'=AC+CD'=5+2=7,∴线段OE的最大值是.
11.1+ ∵+(2-b)2=0,且≥0,(2-b)2≥0,∴a-1=0,2-b=0,解得a=1,b=2,∴原式=+=1+.
12.-10时,x的取值范围是-113.270 1 000×=270.
14.f15.π- 当AP+PQ的值最小时,易知PQ⊥AB,如图1,过点P作PE⊥BC于点E,由BD是∠ABC的平分线,可得PE=PQ,∴PA+PQ=PA+PE.连接AC,∵AB是半圆O的直径,∴∠ACB=90°,∴当点P位于AC与BD的交点处时,PA+PE的值最小,如图2,即PA+PQ的值最小.连接AD,∵AB是半圆O的直径,∴∠ADB=90°,∴AD=ABsin∠ABD=4sin 30°=2.∵∠DAC=∠DBC=30°,∴DP=ADtan∠DAC=2tan 30°=,∴S△DAP=AD·DP=×2×=.连接OD,则∠AOD=2∠ABD=60°,又OA=OD,∴△AOD为等边三角形,∴S弓形AD=S扇形AOD-S△AOD=-×2×=π-,∴S阴影部分=S△DAP+S弓形AD=+π-=π-.
图1 图2
16.【参考答案】原式=2-1+1+3-+2 023[()2+()2] (5分)
=2-1+1+3-5+2 023(+)
=2 023. (7分)
17.【参考答案】(1)如图1,△DEF即为所求. (3分)
图1 图2
(2)如图2,△MNL即为所求. (7分)
(本题答案不唯一,所画图形满足题意即可得分)
18.【参考答案】(1)8 0.35 (2分)
m=40×0.2=8,n==0.35.
(2)补全频数分布直方图略. (3分)
(3)成绩在94.5分以上的选手共4人,男生和女生各占一半,因此有2名男生(分别记为男1、男2)和2名女生(分别记为女1、女2).由题意列表如下:
(6分)
由上表可知,共有12种等可能的结果,其中恰好是一名男生和一名女生的结果有8种,故所求概率为=. (8分)
19.【参考答案】如图,过点D分别作DE⊥AC交AC的延长线于点E,DF⊥AB于点F,则四边形AFDE是矩形.
∵i=1∶3,∴设DE=x米,CE=3x米. (1分)
在Rt△CED中,x2+(3x)2=102,解得x=(负值不合题意,已舍去),
∴DE= 米,CE=3 米. (4分)
易知∠DBF=∠BDF=45°,∴BF=DF.
设BF=DF=m米,则AB=(m+)米,AC=(m-3)米. (6分)
在Rt△CAB中,tan 58.5°==,即m+=tan 58.5°·(m-3),
解得m≈29.92,∴AB=29.92+≈33.1(米).
答:雕像AB的高度约为33.1米. (9分)
20.【参考答案】(1)证明:∵AD是☉O的直径,AD⊥BC,
∴=,∴AB=AC.
∵AD⊥BC,∴∠BAD=∠CAD. (4分)
(2)∵BE=,∴BC=2BE=2.
设☉O的半径为x,则OE=x-1.在Rt△OBE中,OB2=OE2+BE2,
即x2=(x-1)2+()2,解得x=2.
由题意得,BG是☉O的直径,∴∠BCG=90°.
在Rt△BCG中,GC==2. (8分)
∵AD⊥BC,∴AE∥GC,∴△AOF∽△CGF,∴=.
∵OA=GC,∴OF=GF=OG=1. (10分)
21.【参考答案】(1)证明:如图2,过点C作CE∥DA,交BA的延长线于点E.
∵CE∥AD,∴=,∠2=∠ACE,∠1=∠E. (3分)
∵∠1=∠2,∴∠ACE=∠E,∴AE=AC,∴=. (5分)
(2)∵AB=3,BC=4,∠ABC=90°,∴AC=5.
∵AD平分∠BAC,∴=,即=,∴BD=BC=, (7分)
∴在Rt△ADB中,AD===, (9分)
∴△ABD的周长=+3+=. (11分)
22.【参考答案】(1)不是 (2分)
解方程x2-5x+6=0得,x1=2,x2=3,得x1≠x2,∴方程x2-5x+6=0不是“半根方程”.
(2)∵关于x的方程(x-4)(mx+n)=0是“半根方程”,
∴解得x1=4,x2=-, (3分)
结合“半根方程”的定义可知,x2=2或x2=8.
当x2=2时,2m+n=0,∴=-,
当x2=8时,8m+n=0,=-.故的值为-或-. (5分)
(3)证明:方程x2+bx+c=0的根为x1=,x2=, (6分)
根据题意可分为以下两种情况讨论.
①当x1=2x2时,=×2,即-×2=0,∴=0,∴b+3=0,∴3=-b,∴9(b2-4c)=b2,∴2b2=9c. (8分)
②当2x1=x2时,×2=,即×2-=0,∴=0,
∴-b+3=0,∴b=3,∴b2=9(b2-4c),∴2b2=9c. (10分)
故当关于x的方程x2+bx+c=0是“半根方程”时,满足2b2=9c. (11分)
23.【参考答案】(1)将点A(-,0)代入抛物线F1的表达式,得a(--)2+=0,解得a=-,∴y=-(x-)2+=-x2+x+4,
故抛物线F1的表达式为y=-x2+x+4. (3分)
(2)①根据题意知,抛物线F2的表达式为y=-(x-+1)2+-3,
即y=-(x+)2+=-x2-2x+.
由题意得解得则点D的坐标为(-1,1). (5分)
②△BCD是等腰直角三角形.理由如下:
对于y=-x2+x+4,当y=0时,-x2+x+4=0,解得x=2或x=-,
则点B的坐标为(2,0).
当x=0时,y=4,则点C的坐标为(0,4),
∴BC==2,BD==,
CD==,
则BD=CD,BD2+CD2=BC2,∴∠BDC=90°,
故△BCD是等腰直角三角形. (7分)
(3)存在. (8分)
设点P的坐标为(m,n),根据题意可分以下三种情况.
①当∠PDB=90°,PD=BD时,△BDP为等腰直角三角形,
∵△BCD是等腰直角三角形,∠BDC=90°,BD=CD,
∴PD=CD,C,D,P三点共线,∴点D是CP的中点,
则解得即点P的坐标为(-2,-2).
对于抛物线F2:y=-x2-2x+,当x=-2时,y=-×(-2)2-2×(-2)+=-2,
即点P(-2,-2)在抛物线F2上,符合题意.
②当∠PBD=90°,PB=BD时,△BDP为等腰直角三角形,
∵∠BDC=∠PBD=90°,BD=CD,∴CD∥PB,PB=CD,
∴四边形BCDP是平行四边形,
∴点C至点B的平移方式与点D至点P的平移方式相同.
∵C(0,4),B(2,0),∴点C至点B的平移方式为先向下平移4个单位长度,再向右平移2个单位长度.
∵D(-1,1),P(m,n),
∴m=-1+2=1,n=1-4=-3,即点P的坐标为(1,-3).
对于抛物线F2:y=-x2-2x+,当x=1时,y=-×12-2×1+=-3,
即点P(1,-3)在抛物线F2上,符合题意.
③当∠BPD=90°,PB=PD时,△BDP为等腰直角三角形,
则点P在线段BD的垂直平分线上,
设直线BD的表达式为y=kx+b,
将点B(2,0),D(-1,1)分别代入,得解得
则直线BD的表达式为y=-x+.
设线段BD的垂直平分线所在直线的表达式为y=3x+c,
BD的中点的坐标为(,),即(,),
将点(,)代入y=3x+c,得+c=,解得c=-1,
则线段BD的垂直平分线所在直线的表达式为y=3x-1,
则点P的坐标为(m,3m-1),∴PB==.
∵BD=,△BDP为等腰直角三角形,∴PB=BD=,
则=,解得m=0或m=1.
当m=0时,3m-1=3×0-1=-1,即点P的坐标为(0,-1);
当m=1时,3m-1=3×1-1=2,即点P的坐标为(1,2).
对于抛物线F2:y=-x2-2x+,当x=0时,y=-×02-2×0+=,
即点P(0,-1)不在抛物线F2上,不符合题意,舍去.
当x=1时,y=-×12-2×1+=-3.
即点P(1,2)不在抛物线F2上,不符合题意,舍去.
综上,符合条件的点P的坐标为(-2,-2)或(1,-3). (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华师版九年级数学下学期单元测试卷
期末测试卷
时间:100分钟 满分:120分
一、选择题(每小题3分,共30分)
1.二次函数y=-2(x+2)2的图象的顶点坐标是 ( )
A.(-2,0) B.(-2,2) C.(2,0) D.(2,-2)
2.下列计算正确的是 ( )
A.+= B.-8-=-7
C.×=4 D.=
3.下列说法,正确的是 ( )
A.“打开电视,正在播放中央电视台新闻”是必然事件
B.某种彩票中奖概率为10%是指买十张一定有一张中奖
C.神舟飞船发射前需要对零部件进行抽样调查
D.了解某种节能灯的使用寿命适合抽样调查
4.关于x的一元二次方程x2-3mx-13=0的根的情况是 ( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.没有实数根 D.无法确定
5.若关于x的二次函数y=ax2+bx+c的图象如图所示,则下列判断不正确的( )
A.a>0 B.abc<0 C.b>0 D.c>0
6.袋中有除颜色以外其余都相同的红球3个,黄球2个,摇匀后,从中任意摸出1个球,记录下颜色后放回、摇匀,再从中任意摸出1个球,像这样有放回地先后摸球3次,摸到的都是红球,则第4次摸到红球的概率是 ( )
A.1 B.0 C. D.
7.我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形组成的一个大正方形.如果大正方形的面积是100,小正方形的面积是20,那么sin θ-cos θ的值是 ( )
A. B.- C. D.
8.如图,AC,BC分别是半圆O和半圆O'的直径,半圆O的弦MC交半圆O'于点N.若MN=2,∠MCA=30°,则AB= ( )
A. B.4 C. D.1
9.如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,CD=AB,点E,F分别为AB,AD的中点,则△AEF与多边形BCDFE的面积比为 ( )
A. B. C. D.
10.如图,抛物线y=-x2+1与x轴交于A,B两点,D是以点C(0,-3)为圆心,2为半径的圆上的动点,E是线段BD的中点,连接OE,则线段OE的最大值是 ( )
A.2 B. C.3 D.
二、填空题(每小题3分,共15分)
11.如果+(2-b)2=0,那么+= .
12.如图,抛物线y=ax2+bx+c(a≠0)与x轴的一个交点的坐标是(-1,0),当y>0时,x的取值范围是 .
13.某校共有1 000名学生.为了解学生的中长跑成绩分布情况,随机抽取100名学生的中长跑成绩,画出条形统计图,如图.根据所学的统计知识可估计该校中长跑成绩优秀的学生人数是 .
14.我们知道,若抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,则一元二次方程ax2+bx+c=0有两个不相等的实数根.由此,若d,e(d
三、解答题(共75分)
16.(7分)化简:|1-|+(2022-)0+-()-1+2 023(sin260°+cos260°).
17.(7分)如图,在5×5的方格纸中,已知格点三角形ABC,请按要求画图.
(1)在图1的方格纸中画一个格点三角形DEF,使△DEF∽△ABC,且△DEF
与△ABC 的周长比是2∶1.
(2)在图2的方格纸中画一个格点三角形MNL,使△MNL与△ABC相似,且△MNL与△ABC的面积比是2∶1.
图1 图2
18.(8分)某市开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了如下尚不完整的统计图表.
(1)表中m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)选拔赛中,成绩在94.5分以上的选手中,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列表法或画树状图法求恰好是一名男生和一名女生的概率.
19.(9分)大汉雄风坐落于河南省永城市芒砀山主峰,是为纪念刘邦在芒砀山斩蛇起义创建四百年大汉王朝而建.某数学兴趣小组想测量底座之上部分雕像
AB的高度,如图,在山坡上C处测得雕像顶端B的仰角为58.5°,沿山坡向上行走10米到达点D,测得雕像顶端B的仰角为45°,已知山坡的坡度i=1∶3,且A,C在同一水平线上,求雕像AB的高度.(测倾器高度忽略不计,结果精确到0.1米.参考数据:sin 58.5°≈0.85,cos 58.5°≈0.52,tan 58.5°≈1.63,≈1.4,≈1.7,≈3.2)
20.(10分)如图,☉O是△ABC的外接圆,AD是☉O的直径,AD⊥BC于点E.
(1)求证:∠BAD=∠CAD.
(2)连接BO并延长,交AC于点F,交☉O于点G,连接GC,若DE=1,BE=,求GC和OF的长.
21.(11分)请阅读以下材料,并回答下列相应的问题.
角平分线分线段成比例定理的几何语言如下:如图1,在△ABC中,∵AD平分∠BAC,∴=.下面是这个定理的部分证明过程.
证明:如图2,过点C作CE∥DA,交BA的延长线于点E……
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知在Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,求△ABD的周长.
图1 图2 图3
22.(11分)定义:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的一半,则称这样的方程为“半根方程”.
(1)方程x2-5x+6=0 “半根方程”; (填“是”或“不是”)
(2)若关于x的方程(x-4)(mx+n)=0是“半根方程”,求的值;
(3)若关于x的方程x2+bx+c=0是“半根方程”,求证:2b2=9c.
23.(12分)如图1,在平面直角坐标系中,抛物线F1:y=a(x-)2+与x轴交于点A(-,0)和点B,与y轴交于点C.
(1)求抛物线F1的表达式.
(2)如图2,将抛物线F1先向左平移1个单位长度,再向下平移3个单位长度,得到抛物线F2,若抛物线F1与抛物线F2相交于点D,连接BD,CD,BC.
①求点D的坐标;
②判断△BCD的形状,并说明理由.
(3)在2的条件下,抛物线F2上是否存在点P,使得△BDP为等腰直角三角形 若存在,求出点P的坐标;若不存在,请说明理由.
图1 图2
参考答案与解析
1.A
2.C +=+2,-8-=-9,×==4,=.
3.D “打开电视,正在播放中央电视台新闻”是随机事件;某种彩票中奖概率为10%是指买十张可能中奖,也可能不中奖;神舟飞船发射前需要对零部件进行全面调查;了解某种节能灯的使用寿命,具有破坏性,适合抽样调查.故选D.
4.B 根据题意,得Δ=(-3m)2-4×1×(-13)=9m2+52.因为无论m为何值,9m2
≥0恒成立,所以9m2+52>0,所以一元二次方程x2-3mx-13=0有两个不相等的实数根.
5.B 因为抛物线开口向上,所以a>0.因为抛物线的对称轴在y轴左侧,所以
-<0,所以b>0.因为抛物线与y轴的正半轴相交,所以c>0,所以abc>0.
6.C 因为是有放回地摸球,所以每次红球被摸到的概率跟摸球的次数没有关系,所以在有3个红球,2个黄球的前提下,第4次摸到红球的概率是.
7.B ∵大正方形的面积是100,小正方形的面积是20,∴大正方形的边长为10,小正方形的边长为2,∴10cos θ-10sin θ=2,∴cos θ-sin θ=,∴sin θ -cos θ=-.
8.A ∵AC,BC分别是半圆O和半圆O'的直径,∴∠AMC=∠BNC=90°,∴
cos 30°===,∴CM=AC,CN=BC.∵MN=CM-CN=2,∴AC-BC=2,∴(AC-BC)×=2,即AB×=2,∴AB=.
9.C 如图,连接BD.∵F,E分别为AD,AB的中点,∴EF=BD,EF∥BD,∴△AEF∽△ABD,∴=()2=()2=,∴S△ABD=4S△AEF,∴S四边形BDFE=3S△AEF.∵====2,∴S△ABD=2S△BCD,∴S△BCD=2S△AEF,∴
==.
10.D 如图,连接AD,当y=0时,-x2+1=0,解得x1=4,x2=-4,∴A(-4,0),B(4,0).∵E是线段BD的中点,∴OE为△ABD的中位线,∴OE=
AD,即当AD最大时,OE最大,显然AD经过圆心C时,AD最大,即点D运动到点D'位置时,AD最大.∵AC==5,∴AD'=AC+CD'=5+2=7,∴线段OE的最大值是.
11.1+ ∵+(2-b)2=0,且≥0,(2-b)2≥0,∴a-1=0,2-b=0,解得a=1,b=2,∴原式=+=1+.
12.-1
14.f
图1 图2
16.【参考答案】原式=2-1+1+3-+2 023[()2+()2] (5分)
=2-1+1+3-5+2 023(+)
=2 023. (7分)
17.【参考答案】(1)如图1,△DEF即为所求. (3分)
图1 图2
(2)如图2,△MNL即为所求. (7分)
(本题答案不唯一,所画图形满足题意即可得分)
18.【参考答案】(1)8 0.35 (2分)
m=40×0.2=8,n==0.35.
(2)补全频数分布直方图略. (3分)
(3)成绩在94.5分以上的选手共4人,男生和女生各占一半,因此有2名男生(分别记为男1、男2)和2名女生(分别记为女1、女2).由题意列表如下:
(6分)
由上表可知,共有12种等可能的结果,其中恰好是一名男生和一名女生的结果有8种,故所求概率为=. (8分)
19.【参考答案】如图,过点D分别作DE⊥AC交AC的延长线于点E,DF⊥AB于点F,则四边形AFDE是矩形.
∵i=1∶3,∴设DE=x米,CE=3x米. (1分)
在Rt△CED中,x2+(3x)2=102,解得x=(负值不合题意,已舍去),
∴DE= 米,CE=3 米. (4分)
易知∠DBF=∠BDF=45°,∴BF=DF.
设BF=DF=m米,则AB=(m+)米,AC=(m-3)米. (6分)
在Rt△CAB中,tan 58.5°==,即m+=tan 58.5°·(m-3),
解得m≈29.92,∴AB=29.92+≈33.1(米).
答:雕像AB的高度约为33.1米. (9分)
20.【参考答案】(1)证明:∵AD是☉O的直径,AD⊥BC,
∴=,∴AB=AC.
∵AD⊥BC,∴∠BAD=∠CAD. (4分)
(2)∵BE=,∴BC=2BE=2.
设☉O的半径为x,则OE=x-1.在Rt△OBE中,OB2=OE2+BE2,
即x2=(x-1)2+()2,解得x=2.
由题意得,BG是☉O的直径,∴∠BCG=90°.
在Rt△BCG中,GC==2. (8分)
∵AD⊥BC,∴AE∥GC,∴△AOF∽△CGF,∴=.
∵OA=GC,∴OF=GF=OG=1. (10分)
21.【参考答案】(1)证明:如图2,过点C作CE∥DA,交BA的延长线于点E.
∵CE∥AD,∴=,∠2=∠ACE,∠1=∠E. (3分)
∵∠1=∠2,∴∠ACE=∠E,∴AE=AC,∴=. (5分)
(2)∵AB=3,BC=4,∠ABC=90°,∴AC=5.
∵AD平分∠BAC,∴=,即=,∴BD=BC=, (7分)
∴在Rt△ADB中,AD===, (9分)
∴△ABD的周长=+3+=. (11分)
22.【参考答案】(1)不是 (2分)
解方程x2-5x+6=0得,x1=2,x2=3,得x1≠x2,∴方程x2-5x+6=0不是“半根方程”.
(2)∵关于x的方程(x-4)(mx+n)=0是“半根方程”,
∴解得x1=4,x2=-, (3分)
结合“半根方程”的定义可知,x2=2或x2=8.
当x2=2时,2m+n=0,∴=-,
当x2=8时,8m+n=0,=-.故的值为-或-. (5分)
(3)证明:方程x2+bx+c=0的根为x1=,x2=, (6分)
根据题意可分为以下两种情况讨论.
①当x1=2x2时,=×2,即-×2=0,∴=0,∴b+3=0,∴3=-b,∴9(b2-4c)=b2,∴2b2=9c. (8分)
②当2x1=x2时,×2=,即×2-=0,∴=0,
∴-b+3=0,∴b=3,∴b2=9(b2-4c),∴2b2=9c. (10分)
故当关于x的方程x2+bx+c=0是“半根方程”时,满足2b2=9c. (11分)
23.【参考答案】(1)将点A(-,0)代入抛物线F1的表达式,得a(--)2+=0,解得a=-,∴y=-(x-)2+=-x2+x+4,
故抛物线F1的表达式为y=-x2+x+4. (3分)
(2)①根据题意知,抛物线F2的表达式为y=-(x-+1)2+-3,
即y=-(x+)2+=-x2-2x+.
由题意得解得则点D的坐标为(-1,1). (5分)
②△BCD是等腰直角三角形.理由如下:
对于y=-x2+x+4,当y=0时,-x2+x+4=0,解得x=2或x=-,
则点B的坐标为(2,0).
当x=0时,y=4,则点C的坐标为(0,4),
∴BC==2,BD==,
CD==,
则BD=CD,BD2+CD2=BC2,∴∠BDC=90°,
故△BCD是等腰直角三角形. (7分)
(3)存在. (8分)
设点P的坐标为(m,n),根据题意可分以下三种情况.
①当∠PDB=90°,PD=BD时,△BDP为等腰直角三角形,
∵△BCD是等腰直角三角形,∠BDC=90°,BD=CD,
∴PD=CD,C,D,P三点共线,∴点D是CP的中点,
则解得即点P的坐标为(-2,-2).
对于抛物线F2:y=-x2-2x+,当x=-2时,y=-×(-2)2-2×(-2)+=-2,
即点P(-2,-2)在抛物线F2上,符合题意.
②当∠PBD=90°,PB=BD时,△BDP为等腰直角三角形,
∵∠BDC=∠PBD=90°,BD=CD,∴CD∥PB,PB=CD,
∴四边形BCDP是平行四边形,
∴点C至点B的平移方式与点D至点P的平移方式相同.
∵C(0,4),B(2,0),∴点C至点B的平移方式为先向下平移4个单位长度,再向右平移2个单位长度.
∵D(-1,1),P(m,n),
∴m=-1+2=1,n=1-4=-3,即点P的坐标为(1,-3).
对于抛物线F2:y=-x2-2x+,当x=1时,y=-×12-2×1+=-3,
即点P(1,-3)在抛物线F2上,符合题意.
③当∠BPD=90°,PB=PD时,△BDP为等腰直角三角形,
则点P在线段BD的垂直平分线上,
设直线BD的表达式为y=kx+b,
将点B(2,0),D(-1,1)分别代入,得解得
则直线BD的表达式为y=-x+.
设线段BD的垂直平分线所在直线的表达式为y=3x+c,
BD的中点的坐标为(,),即(,),
将点(,)代入y=3x+c,得+c=,解得c=-1,
则线段BD的垂直平分线所在直线的表达式为y=3x-1,
则点P的坐标为(m,3m-1),∴PB==.
∵BD=,△BDP为等腰直角三角形,∴PB=BD=,
则=,解得m=0或m=1.
当m=0时,3m-1=3×0-1=-1,即点P的坐标为(0,-1);
当m=1时,3m-1=3×1-1=2,即点P的坐标为(1,2).
对于抛物线F2:y=-x2-2x+,当x=0时,y=-×02-2×0+=,
即点P(0,-1)不在抛物线F2上,不符合题意,舍去.
当x=1时,y=-×12-2×1+=-3.
即点P(1,2)不在抛物线F2上,不符合题意,舍去.
综上,符合条件的点P的坐标为(-2,-2)或(1,-3). (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
