2024人教版九年级数学下学期单元测试卷--第二十八章锐角三角函数测试卷(含答案)
文档属性
| 名称 | 2024人教版九年级数学下学期单元测试卷--第二十八章锐角三角函数测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024人教版九年级数学下学期单元测试卷
第二十八章 锐角三角函数
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·天津红桥区模拟)如图,在Rt △ABC中,∠B=90°,下列结论正确的是 ( )
A.sin A= B.cos A= C.tan C= D.cos C=
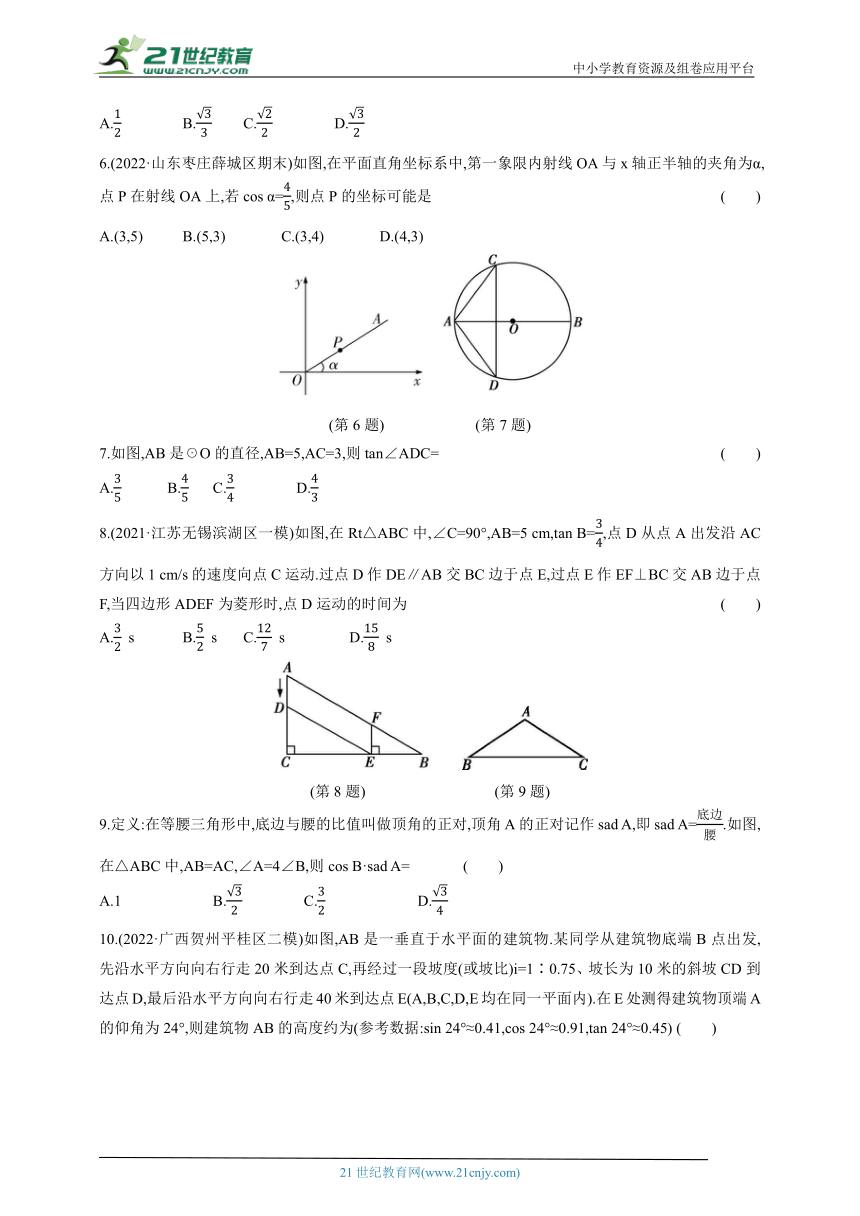
2.(2022·陕西西安长安区期末)在Rt△ABC中,∠C=90°,AC=2,BC=,则cos A的值为 ( )
A. B.3 C. D.
3.按如图所示的运算程序,能使输出y值为的是 ( )
A.α=60°,β=45° B.α=30°,β=45°
C.α=45°,β=30° D.α=30°,β=30°
4.(2021·广东深圳龙岗区二模)“儿童散学归来早,忙趁东风放纸鸢”描绘出一幅充满生机的春天景象.小明周末制作了一只风筝在公园里放飞,如图所示,风筝拉线长100米,且拉线与地面夹角为65°,假设拉线是直的,小明身高忽略不计,则风筝离地面的高度可以表示为 ( )
A.100sin 65° 米 B.100cos 65° 米
C.100tan 65° 米 D.米
(第4题) (第5题)
5.(2022·江苏淮安淮阴区模拟)如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO的长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为 ( )
A. B. C. D.
6.(2022·山东枣庄薛城区期末)如图,在平面直角坐标系中,第一象限内射线OA与x轴正半轴的夹角为α,点P在射线OA上,若cos α=,则点P的坐标可能是 ( )
A.(3,5) B.(5,3) C.(3,4) D.(4,3)
(第6题) (第7题)
7.如图,AB是☉O的直径,AB=5,AC=3,则tan∠ADC= ( )
A. B. C. D.
8.(2021·江苏无锡滨湖区一模)如图,在Rt△ABC中,∠C=90°,AB=5 cm,tan B=,点D从点A出发沿AC方向以1 cm/s的速度向点C运动.过点D作DE∥AB交BC边于点E,过点E作EF⊥BC交AB边于点F,当四边形ADEF为菱形时,点D运动的时间为 ( )
A. s B. s C. s D. s
(第8题) (第9题)
9.定义:在等腰三角形中,底边与腰的比值叫做顶角的正对,顶角A的正对记作sad A,即sad A=.如图,在△ABC中,AB=AC,∠A=4∠B,则cos B·sad A= ( )
A.1 B. C. D.
10.(2022·广西贺州平桂区二模)如图,AB是一垂直于水平面的建筑物.某同学从建筑物底端B点出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)i=1∶0.75、坡长为10米的斜坡CD到达点D,最后沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin 24°≈0.41,cos 24°≈0.91,tan 24°≈0.45) ( )
A.21.7米 B.22.4米 C.27.4米 D.28.8米
二、填空题(共6小题,每小题3分,共18分)
11.(2022·上海徐汇区期中)60°角的 值等于.
12.(2022·四川宜宾二模)在△ABC中,∠A为锐角.若|sin A-|+(-cos B)2=0,则∠C= .
13.在Rt△ABC中,∠C=90°,BC=10,若△ABC的面积为,则∠A= .
14.(2022·湖北武汉中考)如图,沿AB方向架桥修路,为加快施工进度,在直线AB上湖的另一边的D处同时施工.取∠ABC=150°,BC=1 600 m,∠BCD=105°,则C,D两点的距离是 m.
15.(2022·湖南张家界中考)我国魏晋时期的数学家赵爽在为天文学著作《周髀算经》作注解时,用4个全等的直角三角形和中间的小正方形拼成一个大正方形,这个图被称为“弦图”,它体现了中国古代数学的成就.如图,已知大正方形ABCD的面积是100,小正方形EFGH的面积是4,那么tan∠ADF= .
(第15题) (第16题)
16.(2022·福建福州三牧中学一模)如图为两个边长为1的正方形组成的2×1格点图,点A,B,C,D都在格点上,AB,CD交于点P,则tan∠BPD= .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15. 16.
三、解答题(共6小题,共52分)
17.(共2小题,每小题3分,共6分)计算:
(1)sin 60°·tan 30°+.
(2)-2tan 45°·sin 60°.
18.(8分)(2022·江苏泰州海陵区二模)已知△ABC为钝角三角形,其中∠A>90°,有下列条件:
①AB=10;②AC=6;
③tan B=;④tan C=.
(1)你认为从中至少选择 个条件,可以求出BC边的长;
(2)你选择的条件是 (直接填写序号),并写出求BC边的长的解答过程.
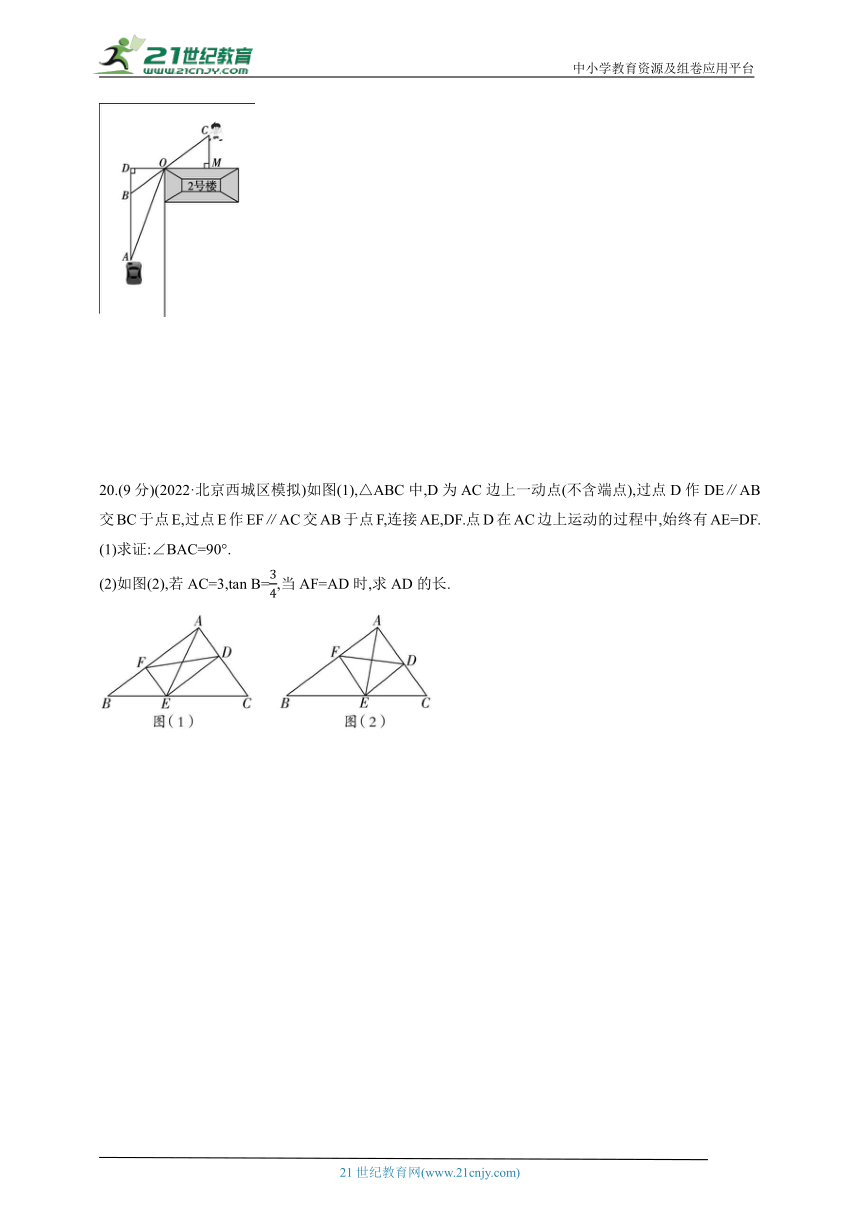
19.(8分)(2021·山东临沂中考)如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来.已知CM=3 m,CO=5 m,DO=3 m,B,O,C共线,∠AOD=70°,汽车从A处前行多少米才能发现C处的儿童(结果保留整数)
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,sin 70°≈0.94,cos 70°≈0.34,tan 70°≈2.75)
20.(9分)(2022·北京西城区模拟)如图(1),△ABC中,D为AC边上一动点(不含端点),过点D作DE∥AB交BC于点E,过点E作EF∥AC交AB于点F,连接AE,DF.点D在AC边上运动的过程中,始终有AE=DF.
(1)求证:∠BAC=90°.
(2)如图(2),若AC=3,tan B=,当AF=AD时,求AD的长.
21. (10分)(2022·陕西西安灞桥区四模改编)如图,在南北方向的海岸线 MN上,有A,B两艘巡逻船,现均收到故障船 C的求救信号.已知A,B两船相距100(+1)海里,船 C在船 A的北偏东 60°方向上,船 C在船 B的东南方向上,MN上有一观测点 D,测得船 C正好在观测点D的南偏东 75°方向上.
(1)分别求出 A与C,A与D之间的距离.(结果有根号的保留根号)
(2)已知距观测点 D处 100海里范围内有暗礁,若巡逻船 A沿直线 AC去营救船 C,在去营救的途中有无触礁危险
(参考数据:≈1.41,≈1.73)
22.(11分)(2022·山东济宁中考)知识再现
如图(1),在Rt △ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
∵sin A=,sin B=,
∴c=,c=,
∴=.
拓展探究
如图(2),在锐角三角形ABC中,∠A,∠B,∠C的对边分别为a,b,c.
请探究,,之间的关系,并写出探究过程.
解决问题
如图(3),为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60 m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.
图(1) 图(2) 图(3)
第二十八章 锐角三角函数
1 2 3 4 5 6 7 8 9 10
C A D A D D C D C A
11.正切 12.105° 13.60°
14.800 15. 16.3
1.C 在Rt△ABC中,∠B=90°,则sin A=,cos A=,tan C=,cos C=.故选C.
2.A
如图,∵∠C=90°,AC=2,BC=,∴AB===3,∴cos A==.
3.D (直接代入法)A选项中,α=60°,β=45°,α>β,则y=sin α=;B选项中,
α=30°,β=45°,α<β,则y=cos β=;C选项中,α=45°,β=30°,α>β,则y=
sin α=;D选项中,α=30°,β=30°,α=β,则y=sin α=.
4.A 如图,过点A作AC⊥BC于点C,在Rt△ABC中,sin B=,即AC=AB·sin B=
100sin 65°(米).
(第4题) (第5题)
5.D 如图,连接BC,由题意可得OB=OC=BC,则△OBC是等边三角形,∴∠AOC=60°,
∴sin∠AOC=sin 60°=.
6.D 如图,过点P作PB⊥x轴于点B,∵cos α==,∴可假设OB=4,则OP=5
∴PB==3,∴点P的坐标可能是(4,3).
7.C 连接BC,∵AB为☉O的直径,∴∠ACB=90°.∵AB=5,AC=3,∴根据勾股定理,得BC=4.∵∠ADC=∠ABC,∴tan∠ADC=tan∠ABC==.
8.D ∵在Rt△ABC中,AB=5 cm,tan B=,∴AC=3 cm,BC=4 cm.设点D运动t s后,四边形ADEF是菱形,∴DE=AD=t cm,CD=(3-t)cm.∵DE∥AB,∴∠ABC=∠DEC,
∴sin∠DEC=sin∠ABC==,即=,解得t=.
9.C ∵在△ABC中,AB=AC,∠A=4∠B,∴∠B=∠C.∵∠A+∠B+∠C=180°,∴6∠B=180°,解得∠B=30°,∴cos B=.如图,过点A作AD⊥BC于点D,设AD=a,则AB=2a,BD=a.∵BC=2BD,∴BC=2a,
∴sad∠BAC===,∴cos B·sad∠BAC=×=.
10.A 如图,延长AB交ED的延长线于点M,过点C作CN⊥DE于点N,则BM⊥ME,且MN=BC=20米.∵斜坡CD的坡度i=1∶0.75,∴令CN=x米,则DN=0.75x米.在Rt△CDN中,有x2+(0.75x)2=102,解得x=8,从而CN=8米,DN=6米.∵DE=40米,
∴ME=MN+ND+DE=20+6+40=66(米).∵在Rt△AME中,tan E=,∴tan 24°=,即0.45≈,解得AB≈21.7(米).故选A.
11.正切
12.105° 由题意得,sin A-=0,-cos B=0,∴sin A=,cos B=,∴∠A=45°,
∠B=30°.∴∠C=105°.
13.60° ∵BC=10,∴S△ABC===,则AC=,∴tan A===,
∴∠A=60°.
14.800 如图,过点C作CE⊥BD,垂足为E,∵∠ABC=150°,∴∠DBC=30°.在Rt△BCE中,∵BC=1 600,∴CE=BC=800,∠BCE=60°.∵∠BCD=105°,∴∠ECD=45°.在Rt△DCE中,∵cos∠ECD=,∴CD===800(m).
15. ∵大正方形ABCD的面积是100,∴AD=10.∵小正方形EFGH的面积是4,
∴FG=2.由题意得,DF=AG,∴DF-AF=AG-AF=FG=2.设AF=x,则DF=x+2,由勾股定理得,
x2+(x+2)2=102,解得x=6(负值已舍去),∴AF=6,DF=8,∴tan∠ADF===.
16.3 如图,连接BE交CD于点O.∵四边形BCED是边长为1的正方形,∴BE⊥
CD,OB=OC=OD=OE=×1=,∴CD=.∵BC∥AD,∴△BCP∽△ADP,∴==,∴CP=
CD=,∴OP=OC-CP=-=.在Rt△BOP中,tan∠BPD===3.
一题多解 如图,作DE⊥AB,垂足为E.在Rt△ABD中,AB===.又AB·DE=AD·BD,∴DE=.∵BC∥AD,∴△BCP∽△ADP,∴==,∴DP=CD==.在Rt△DPE中,PE==,∴tan∠BPD===3.
17.【参考答案】(1)原式=×+÷1 (2分)
=+
=1. (3分)
(2)原式=-1-2×1× (2分)
=-1-
=-1. (3分)
18.【参考答案】(1)3 (2分)
(2)①②④ (3分)
解答过程如下.
如图,过点A作AD⊥BC于点D,
设AD=x,
∵tan C=,
∴CD=2x.
∵AC=6,
∴在Rt△ACD中,根据勾股定理,得x2+(2x)2=(6)2,
解得x=6或x=-6(不合题意,舍去),
∴AD=6,CD=2x=12.
∵AB=10,
∴在Rt△ABD中,根据勾股定理,得BD==8,
∴BC=CD+BD=12+8=20. (8分)
(本大题答案不唯一,也可选择①②③)
一题多解
(2)①②④ (4分)
解答过程如下.
如图,过点B作BE⊥CA,交CA的延长线于点E.
在Rt△BCE中,tan C==,
∴设BE=x,则CE=2x,
∴AE=2x-6.
在Rt△BAE中,由勾股定理得,AE2+BE2=AB2,
即(2x-6)2+x2=102,
解得x=4或x=(不合题意,舍去),
∴BE=4,CE=8,
∴在Rt△BCE中,BC===20.(8分)
(本大题答案不唯一,也可选择①②③)
19.【参考答案】在Rt△COM中,OM===4(m).
∵∠BOD=∠COM,
∴tan∠BOD=tan∠COM,
∴==,
∴BD=2.25 m. (3分)
在Rt△AOD中,AD=OD×tan∠AOD=3×tan 70°≈3×2.75=8.25(m),(6分)
∴AB=AD-BD=8.25-2.25=6(m).
答:汽车从A处前行6 m才能发现C处的儿童. (8分)
20.【参考答案】(1)证明:∵DE∥AB,EF∥AC,
∴四边形ADEF是平行四边形.
∵AE=DF,
∴平行四边形ADEF是矩形,
∴∠BAC=90°. (3分)
(2)当AF=AD时,
由(1)知,此时四边形ADEF是正方形.
∵DE∥AB,
∴∠DEC=∠B,∠EDC=∠BAC=90°,
∴tan∠DEC=tan B=.
在Rt△DEC中,设DC=3x,则DE=4x.
∵四边形ADEF是正方形,
∴AD=DE=4x,
∴AC=AD+DC=7x=3,
∴x=,
∴AD=4x=. (9分)
21.【解题思路】(1)过点C作CE⊥AB于点E,设AE=a海里.根据AB=AE+BE,求得a的值后即可求得AC的长,由三角形相似定理求出AD的长;(2)过点D作DF⊥AC于点F,根据(1)中的结论求出DF的长,再与100比较即可得到答案.
【参考答案】(1)如图,过点C作CE⊥AB于点E.
设AE=a海里,
在Rt△ACE中,∠AEC=90°,∠EAC=60°,
∴AC===2a(海里),
CE=AE·tan 60°=a(海里).
在Rt△BCE中,∠EBC=45°,
∴BE=CE=a海里.
由AB=AE+BE得100(+1)=a+a,
解得a=100,
∴AC=2a=200海里. (4分)
在△ACD和△ABC中,∠ACB=180°-45°-60°=75°=∠ADC,∠CAD=∠BAC,
∴△ACD∽△ABC,
∴=,即=,
∴AD=(200-200)海里.
故A与C之间的距离为200海里,A与D之间的距离为(200-200)海里. (6分)
(2)如图,过点D作DF⊥AC于点F.
在Rt△ADF中,∠DAF=60°,
∴DF=AD·sin 60°=(200-200)×≈127(海里),
∵127>100,
∴巡逻船A在去营救船C的途中无触礁危险. (10分)
22.【参考答案】拓展探究
如图,作△ABC的外接圆☉O,连接BO并延长,交☉O于点D,连接CD,则∠A=∠D.
设☉O的直径为2r.
∵BD是☉O的直径,∴∠BCD=90°.
在Rt△BCD中,sin D=,
∴BD=,即2r=.
同理可得,=2r,=2r,
故==. (5分)
解决问题
在△ABC中,∠B=180°-∠A-∠C=45°.
由拓展探究中的结论,得=,即=,
∴AB===30(m).
答:点A到点B的距离为30 m. (11分)
一题多解
拓展探究
如图,作CD⊥AB于点D,AE⊥BC于点E,
在Rt△ABE中,sin B==,
同理得,sin B==,
sin∠BAC==,
sin∠BCA==,
∴AE=csin B,AE=bsin∠BCA,CD=asin B,CD=bsin∠BAC,
∴=,=,
∴==. (5分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版九年级数学下学期单元测试卷
第二十八章 锐角三角函数
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·天津红桥区模拟)如图,在Rt △ABC中,∠B=90°,下列结论正确的是 ( )
A.sin A= B.cos A= C.tan C= D.cos C=
2.(2022·陕西西安长安区期末)在Rt△ABC中,∠C=90°,AC=2,BC=,则cos A的值为 ( )
A. B.3 C. D.
3.按如图所示的运算程序,能使输出y值为的是 ( )
A.α=60°,β=45° B.α=30°,β=45°
C.α=45°,β=30° D.α=30°,β=30°
4.(2021·广东深圳龙岗区二模)“儿童散学归来早,忙趁东风放纸鸢”描绘出一幅充满生机的春天景象.小明周末制作了一只风筝在公园里放飞,如图所示,风筝拉线长100米,且拉线与地面夹角为65°,假设拉线是直的,小明身高忽略不计,则风筝离地面的高度可以表示为 ( )
A.100sin 65° 米 B.100cos 65° 米
C.100tan 65° 米 D.米
(第4题) (第5题)
5.(2022·江苏淮安淮阴区模拟)如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO的长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为 ( )
A. B. C. D.
6.(2022·山东枣庄薛城区期末)如图,在平面直角坐标系中,第一象限内射线OA与x轴正半轴的夹角为α,点P在射线OA上,若cos α=,则点P的坐标可能是 ( )
A.(3,5) B.(5,3) C.(3,4) D.(4,3)
(第6题) (第7题)
7.如图,AB是☉O的直径,AB=5,AC=3,则tan∠ADC= ( )
A. B. C. D.
8.(2021·江苏无锡滨湖区一模)如图,在Rt△ABC中,∠C=90°,AB=5 cm,tan B=,点D从点A出发沿AC方向以1 cm/s的速度向点C运动.过点D作DE∥AB交BC边于点E,过点E作EF⊥BC交AB边于点F,当四边形ADEF为菱形时,点D运动的时间为 ( )
A. s B. s C. s D. s
(第8题) (第9题)
9.定义:在等腰三角形中,底边与腰的比值叫做顶角的正对,顶角A的正对记作sad A,即sad A=.如图,在△ABC中,AB=AC,∠A=4∠B,则cos B·sad A= ( )
A.1 B. C. D.
10.(2022·广西贺州平桂区二模)如图,AB是一垂直于水平面的建筑物.某同学从建筑物底端B点出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)i=1∶0.75、坡长为10米的斜坡CD到达点D,最后沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin 24°≈0.41,cos 24°≈0.91,tan 24°≈0.45) ( )
A.21.7米 B.22.4米 C.27.4米 D.28.8米
二、填空题(共6小题,每小题3分,共18分)
11.(2022·上海徐汇区期中)60°角的 值等于.
12.(2022·四川宜宾二模)在△ABC中,∠A为锐角.若|sin A-|+(-cos B)2=0,则∠C= .
13.在Rt△ABC中,∠C=90°,BC=10,若△ABC的面积为,则∠A= .
14.(2022·湖北武汉中考)如图,沿AB方向架桥修路,为加快施工进度,在直线AB上湖的另一边的D处同时施工.取∠ABC=150°,BC=1 600 m,∠BCD=105°,则C,D两点的距离是 m.
15.(2022·湖南张家界中考)我国魏晋时期的数学家赵爽在为天文学著作《周髀算经》作注解时,用4个全等的直角三角形和中间的小正方形拼成一个大正方形,这个图被称为“弦图”,它体现了中国古代数学的成就.如图,已知大正方形ABCD的面积是100,小正方形EFGH的面积是4,那么tan∠ADF= .
(第15题) (第16题)
16.(2022·福建福州三牧中学一模)如图为两个边长为1的正方形组成的2×1格点图,点A,B,C,D都在格点上,AB,CD交于点P,则tan∠BPD= .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15. 16.
三、解答题(共6小题,共52分)
17.(共2小题,每小题3分,共6分)计算:
(1)sin 60°·tan 30°+.
(2)-2tan 45°·sin 60°.
18.(8分)(2022·江苏泰州海陵区二模)已知△ABC为钝角三角形,其中∠A>90°,有下列条件:
①AB=10;②AC=6;
③tan B=;④tan C=.
(1)你认为从中至少选择 个条件,可以求出BC边的长;
(2)你选择的条件是 (直接填写序号),并写出求BC边的长的解答过程.
19.(8分)(2021·山东临沂中考)如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来.已知CM=3 m,CO=5 m,DO=3 m,B,O,C共线,∠AOD=70°,汽车从A处前行多少米才能发现C处的儿童(结果保留整数)
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,sin 70°≈0.94,cos 70°≈0.34,tan 70°≈2.75)
20.(9分)(2022·北京西城区模拟)如图(1),△ABC中,D为AC边上一动点(不含端点),过点D作DE∥AB交BC于点E,过点E作EF∥AC交AB于点F,连接AE,DF.点D在AC边上运动的过程中,始终有AE=DF.
(1)求证:∠BAC=90°.
(2)如图(2),若AC=3,tan B=,当AF=AD时,求AD的长.
21. (10分)(2022·陕西西安灞桥区四模改编)如图,在南北方向的海岸线 MN上,有A,B两艘巡逻船,现均收到故障船 C的求救信号.已知A,B两船相距100(+1)海里,船 C在船 A的北偏东 60°方向上,船 C在船 B的东南方向上,MN上有一观测点 D,测得船 C正好在观测点D的南偏东 75°方向上.
(1)分别求出 A与C,A与D之间的距离.(结果有根号的保留根号)
(2)已知距观测点 D处 100海里范围内有暗礁,若巡逻船 A沿直线 AC去营救船 C,在去营救的途中有无触礁危险
(参考数据:≈1.41,≈1.73)
22.(11分)(2022·山东济宁中考)知识再现
如图(1),在Rt △ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
∵sin A=,sin B=,
∴c=,c=,
∴=.
拓展探究
如图(2),在锐角三角形ABC中,∠A,∠B,∠C的对边分别为a,b,c.
请探究,,之间的关系,并写出探究过程.
解决问题
如图(3),为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60 m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.
图(1) 图(2) 图(3)
第二十八章 锐角三角函数
1 2 3 4 5 6 7 8 9 10
C A D A D D C D C A
11.正切 12.105° 13.60°
14.800 15. 16.3
1.C 在Rt△ABC中,∠B=90°,则sin A=,cos A=,tan C=,cos C=.故选C.
2.A
如图,∵∠C=90°,AC=2,BC=,∴AB===3,∴cos A==.
3.D (直接代入法)A选项中,α=60°,β=45°,α>β,则y=sin α=;B选项中,
α=30°,β=45°,α<β,则y=cos β=;C选项中,α=45°,β=30°,α>β,则y=
sin α=;D选项中,α=30°,β=30°,α=β,则y=sin α=.
4.A 如图,过点A作AC⊥BC于点C,在Rt△ABC中,sin B=,即AC=AB·sin B=
100sin 65°(米).
(第4题) (第5题)
5.D 如图,连接BC,由题意可得OB=OC=BC,则△OBC是等边三角形,∴∠AOC=60°,
∴sin∠AOC=sin 60°=.
6.D 如图,过点P作PB⊥x轴于点B,∵cos α==,∴可假设OB=4,则OP=5
∴PB==3,∴点P的坐标可能是(4,3).
7.C 连接BC,∵AB为☉O的直径,∴∠ACB=90°.∵AB=5,AC=3,∴根据勾股定理,得BC=4.∵∠ADC=∠ABC,∴tan∠ADC=tan∠ABC==.
8.D ∵在Rt△ABC中,AB=5 cm,tan B=,∴AC=3 cm,BC=4 cm.设点D运动t s后,四边形ADEF是菱形,∴DE=AD=t cm,CD=(3-t)cm.∵DE∥AB,∴∠ABC=∠DEC,
∴sin∠DEC=sin∠ABC==,即=,解得t=.
9.C ∵在△ABC中,AB=AC,∠A=4∠B,∴∠B=∠C.∵∠A+∠B+∠C=180°,∴6∠B=180°,解得∠B=30°,∴cos B=.如图,过点A作AD⊥BC于点D,设AD=a,则AB=2a,BD=a.∵BC=2BD,∴BC=2a,
∴sad∠BAC===,∴cos B·sad∠BAC=×=.
10.A 如图,延长AB交ED的延长线于点M,过点C作CN⊥DE于点N,则BM⊥ME,且MN=BC=20米.∵斜坡CD的坡度i=1∶0.75,∴令CN=x米,则DN=0.75x米.在Rt△CDN中,有x2+(0.75x)2=102,解得x=8,从而CN=8米,DN=6米.∵DE=40米,
∴ME=MN+ND+DE=20+6+40=66(米).∵在Rt△AME中,tan E=,∴tan 24°=,即0.45≈,解得AB≈21.7(米).故选A.
11.正切
12.105° 由题意得,sin A-=0,-cos B=0,∴sin A=,cos B=,∴∠A=45°,
∠B=30°.∴∠C=105°.
13.60° ∵BC=10,∴S△ABC===,则AC=,∴tan A===,
∴∠A=60°.
14.800 如图,过点C作CE⊥BD,垂足为E,∵∠ABC=150°,∴∠DBC=30°.在Rt△BCE中,∵BC=1 600,∴CE=BC=800,∠BCE=60°.∵∠BCD=105°,∴∠ECD=45°.在Rt△DCE中,∵cos∠ECD=,∴CD===800(m).
15. ∵大正方形ABCD的面积是100,∴AD=10.∵小正方形EFGH的面积是4,
∴FG=2.由题意得,DF=AG,∴DF-AF=AG-AF=FG=2.设AF=x,则DF=x+2,由勾股定理得,
x2+(x+2)2=102,解得x=6(负值已舍去),∴AF=6,DF=8,∴tan∠ADF===.
16.3 如图,连接BE交CD于点O.∵四边形BCED是边长为1的正方形,∴BE⊥
CD,OB=OC=OD=OE=×1=,∴CD=.∵BC∥AD,∴△BCP∽△ADP,∴==,∴CP=
CD=,∴OP=OC-CP=-=.在Rt△BOP中,tan∠BPD===3.
一题多解 如图,作DE⊥AB,垂足为E.在Rt△ABD中,AB===.又AB·DE=AD·BD,∴DE=.∵BC∥AD,∴△BCP∽△ADP,∴==,∴DP=CD==.在Rt△DPE中,PE==,∴tan∠BPD===3.
17.【参考答案】(1)原式=×+÷1 (2分)
=+
=1. (3分)
(2)原式=-1-2×1× (2分)
=-1-
=-1. (3分)
18.【参考答案】(1)3 (2分)
(2)①②④ (3分)
解答过程如下.
如图,过点A作AD⊥BC于点D,
设AD=x,
∵tan C=,
∴CD=2x.
∵AC=6,
∴在Rt△ACD中,根据勾股定理,得x2+(2x)2=(6)2,
解得x=6或x=-6(不合题意,舍去),
∴AD=6,CD=2x=12.
∵AB=10,
∴在Rt△ABD中,根据勾股定理,得BD==8,
∴BC=CD+BD=12+8=20. (8分)
(本大题答案不唯一,也可选择①②③)
一题多解
(2)①②④ (4分)
解答过程如下.
如图,过点B作BE⊥CA,交CA的延长线于点E.
在Rt△BCE中,tan C==,
∴设BE=x,则CE=2x,
∴AE=2x-6.
在Rt△BAE中,由勾股定理得,AE2+BE2=AB2,
即(2x-6)2+x2=102,
解得x=4或x=(不合题意,舍去),
∴BE=4,CE=8,
∴在Rt△BCE中,BC===20.(8分)
(本大题答案不唯一,也可选择①②③)
19.【参考答案】在Rt△COM中,OM===4(m).
∵∠BOD=∠COM,
∴tan∠BOD=tan∠COM,
∴==,
∴BD=2.25 m. (3分)
在Rt△AOD中,AD=OD×tan∠AOD=3×tan 70°≈3×2.75=8.25(m),(6分)
∴AB=AD-BD=8.25-2.25=6(m).
答:汽车从A处前行6 m才能发现C处的儿童. (8分)
20.【参考答案】(1)证明:∵DE∥AB,EF∥AC,
∴四边形ADEF是平行四边形.
∵AE=DF,
∴平行四边形ADEF是矩形,
∴∠BAC=90°. (3分)
(2)当AF=AD时,
由(1)知,此时四边形ADEF是正方形.
∵DE∥AB,
∴∠DEC=∠B,∠EDC=∠BAC=90°,
∴tan∠DEC=tan B=.
在Rt△DEC中,设DC=3x,则DE=4x.
∵四边形ADEF是正方形,
∴AD=DE=4x,
∴AC=AD+DC=7x=3,
∴x=,
∴AD=4x=. (9分)
21.【解题思路】(1)过点C作CE⊥AB于点E,设AE=a海里.根据AB=AE+BE,求得a的值后即可求得AC的长,由三角形相似定理求出AD的长;(2)过点D作DF⊥AC于点F,根据(1)中的结论求出DF的长,再与100比较即可得到答案.
【参考答案】(1)如图,过点C作CE⊥AB于点E.
设AE=a海里,
在Rt△ACE中,∠AEC=90°,∠EAC=60°,
∴AC===2a(海里),
CE=AE·tan 60°=a(海里).
在Rt△BCE中,∠EBC=45°,
∴BE=CE=a海里.
由AB=AE+BE得100(+1)=a+a,
解得a=100,
∴AC=2a=200海里. (4分)
在△ACD和△ABC中,∠ACB=180°-45°-60°=75°=∠ADC,∠CAD=∠BAC,
∴△ACD∽△ABC,
∴=,即=,
∴AD=(200-200)海里.
故A与C之间的距离为200海里,A与D之间的距离为(200-200)海里. (6分)
(2)如图,过点D作DF⊥AC于点F.
在Rt△ADF中,∠DAF=60°,
∴DF=AD·sin 60°=(200-200)×≈127(海里),
∵127>100,
∴巡逻船A在去营救船C的途中无触礁危险. (10分)
22.【参考答案】拓展探究
如图,作△ABC的外接圆☉O,连接BO并延长,交☉O于点D,连接CD,则∠A=∠D.
设☉O的直径为2r.
∵BD是☉O的直径,∴∠BCD=90°.
在Rt△BCD中,sin D=,
∴BD=,即2r=.
同理可得,=2r,=2r,
故==. (5分)
解决问题
在△ABC中,∠B=180°-∠A-∠C=45°.
由拓展探究中的结论,得=,即=,
∴AB===30(m).
答:点A到点B的距离为30 m. (11分)
一题多解
拓展探究
如图,作CD⊥AB于点D,AE⊥BC于点E,
在Rt△ABE中,sin B==,
同理得,sin B==,
sin∠BAC==,
sin∠BCA==,
∴AE=csin B,AE=bsin∠BCA,CD=asin B,CD=bsin∠BAC,
∴=,=,
∴==. (5分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
