2024人教版九年级数学下学期单元测试卷--第二十九章投影与视图测试卷(含答案)
文档属性
| 名称 | 2024人教版九年级数学下学期单元测试卷--第二十九章投影与视图测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024人教版九年级数学下学期单元测试卷
第二十九章 投影与视图
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.下列现象不属于投影的是 ( )
A.皮影 B.素描画 C.手影 D.树影
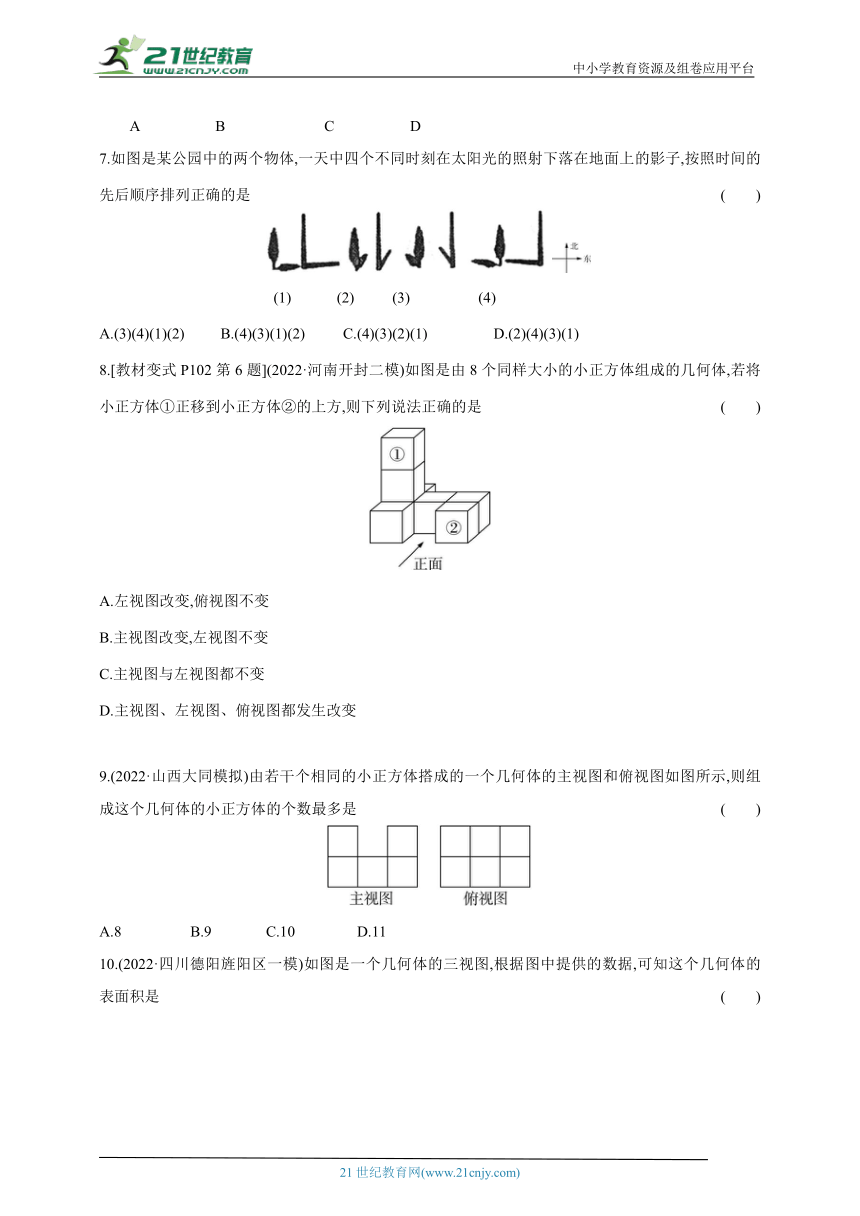
2.(2022·湖北黄冈中考改编)某几何体的三视图如图所示,则该几何体是 ( )
A.圆锥 B.三棱锥 C.四棱柱 D.三棱柱
(第2题) (第3题)
3. (2022·四川成都龙泉驿区模拟)唐代诗人李白《日出行》中有:“日出东方隈,似从地底来.”描述的是看日出的景象,意思是太阳从东方升起,似从地底而来.如图所示,此时观测到地平线和太阳所成的视图可能是 ( )
A B C D
4.(2021·四川成都模拟)如图,晚上小明在路灯下从A处径直走到B处,这一过程中他在地上的影子
( )
A.一直都在变短 B.先变短后变长
C.一直都在变长 D.先变长后变短
5.当某一几何体在投影面P前的摆放位置确定以后,改变它与投影面P的距离,其正投影的形状 ( )
A.不发生变化 B.变大 C.变小 D.无法确定
6.[教材变式P93第5题](2022·北京朝阳区二模)在太阳光的照射下,一个矩形框在水平地面上形成的投影不可能是 ( )
A B C D
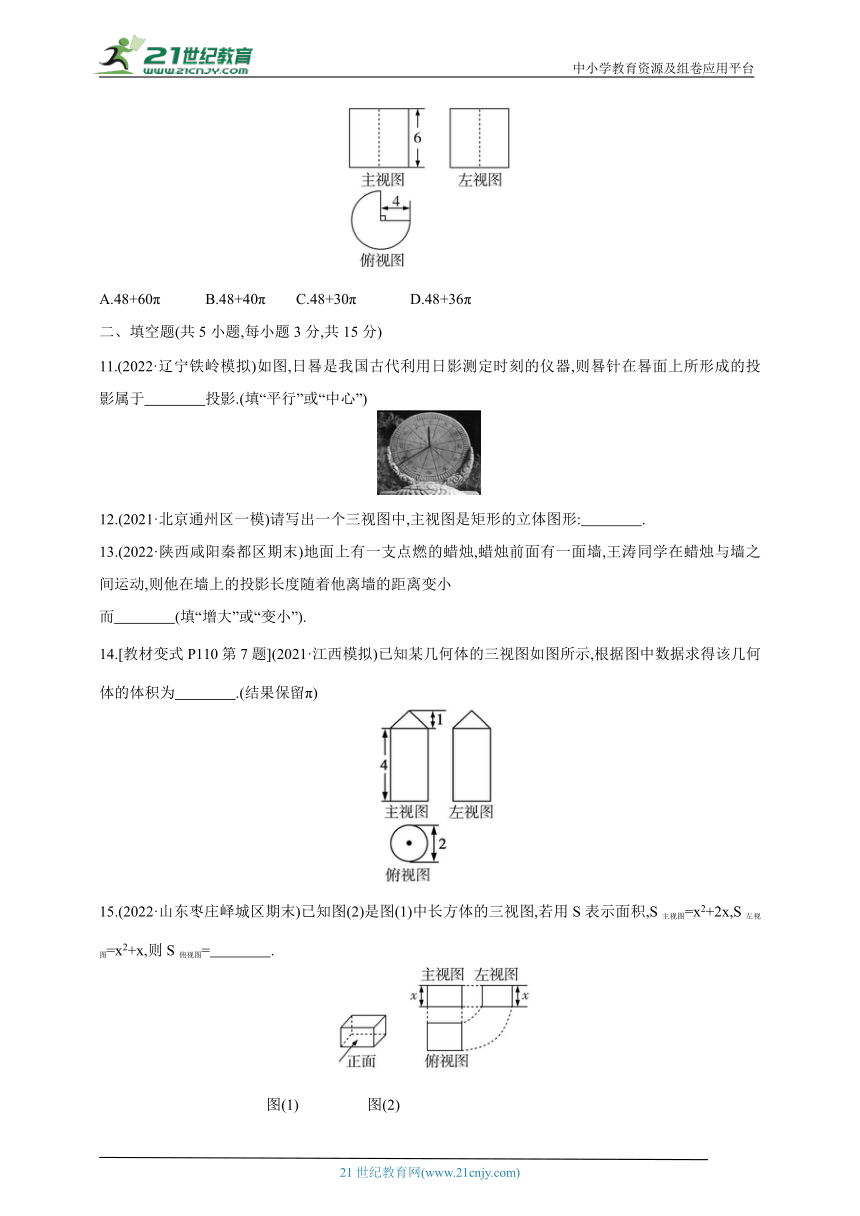
7.如图是某公园中的两个物体,一天中四个不同时刻在太阳光的照射下落在地面上的影子,按照时间的先后顺序排列正确的是 ( )
(1) (2) (3) (4)
A.(3)(4)(1)(2) B.(4)(3)(1)(2) C.(4)(3)(2)(1) D.(2)(4)(3)(1)
8.[教材变式P102第6题](2022·河南开封二模)如图是由8个同样大小的小正方体组成的几何体,若将小正方体①正移到小正方体②的上方,则下列说法正确的是 ( )
A.左视图改变,俯视图不变
B.主视图改变,左视图不变
C.主视图与左视图都不变
D.主视图、左视图、俯视图都发生改变
9.(2022·山西大同模拟)由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数最多是 ( )
A.8 B.9 C.10 D.11
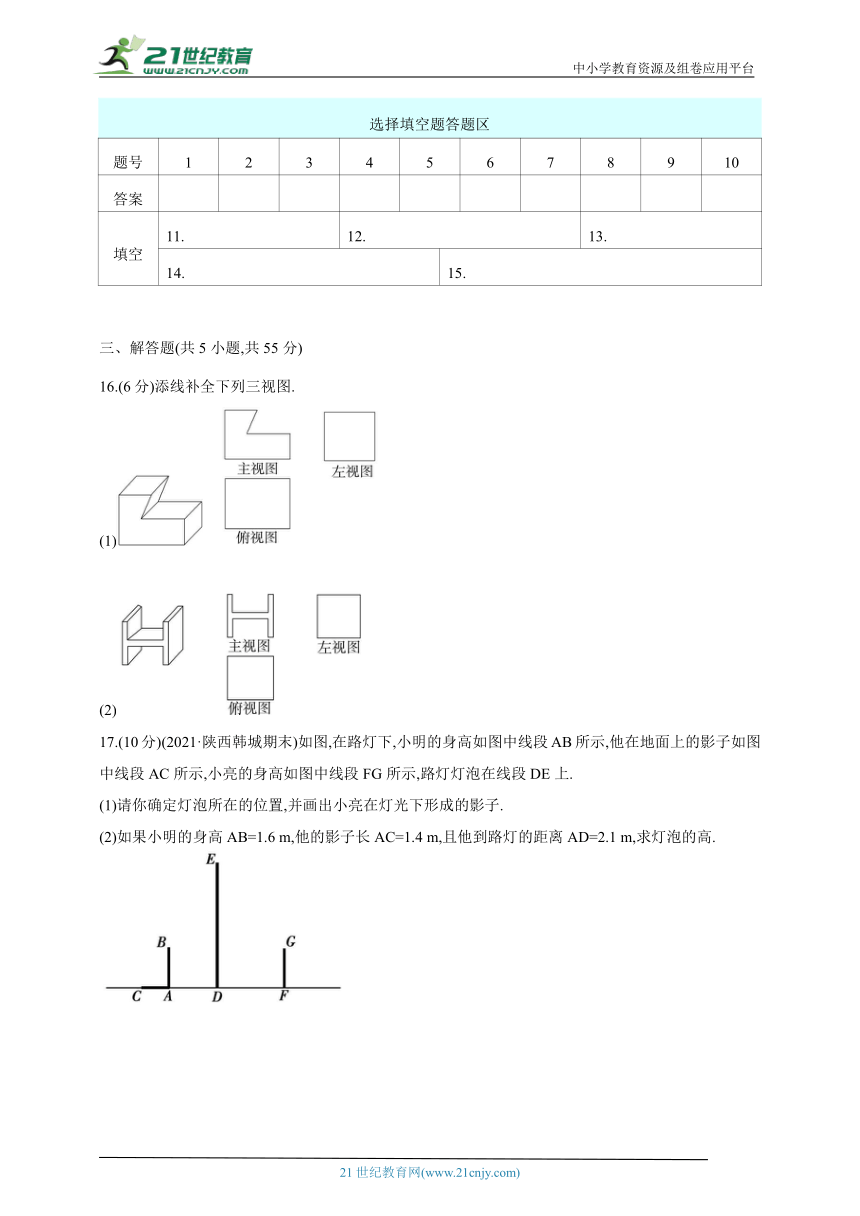
10.(2022·四川德阳旌阳区一模)如图是一个几何体的三视图,根据图中提供的数据,可知这个几何体的表面积是 ( )
A.48+60π B.48+40π C.48+30π D.48+36π
二、填空题(共5小题,每小题3分,共15分)
11.(2022·辽宁铁岭模拟)如图,日晷是我国古代利用日影测定时刻的仪器,则晷针在晷面上所形成的投影属于 投影.(填“平行”或“中心”)
12.(2021·北京通州区一模)请写出一个三视图中,主视图是矩形的立体图形: .
13.(2022·陕西咸阳秦都区期末)地面上有一支点燃的蜡烛,蜡烛前面有一面墙,王涛同学在蜡烛与墙之间运动,则他在墙上的投影长度随着他离墙的距离变小
而 (填“增大”或“变小”).
14.[教材变式P110第7题](2021·江西模拟)已知某几何体的三视图如图所示,根据图中数据求得该几何体的体积为 .(结果保留π)
15.(2022·山东枣庄峄城区期末)已知图(2)是图(1)中长方体的三视图,若用S表示面积,S主视图=x2+2x,S左视图=x2+x,则S俯视图= .
图(1) 图(2)
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15.
三、解答题(共5小题,共55分)
16.(6分)添线补全下列三视图.
(1)
(2)
17.(10分)(2021·陕西韩城期末)如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6 m,他的影子长AC=1.4 m,且他到路灯的距离AD=2.1 m,求灯泡的高.
18.(12分)[教材变式P110第7题](2022·辽宁铁岭模拟改编)如图(1)是一个直四棱柱,如图(2)是它的三视图,其俯视图是等腰梯形.
(1)根据图(2)中的数据,可知a= ,b= ,c= ,d= .
(2)请你根据图(1)和问题(1)中的结果,计算这个直四棱柱的侧面积.(结果可保留根号)
图(1) 图(2)
19.(13分)在“测量物体的高度” 活动中,某数学兴趣小组的3名同学选择了测量学校里的3棵树的高度.在同一时刻的阳光下,他们分别做了以下工作:
小芳:测得一根长为1 m的竹竿的影长为0.8 m,甲树的影长为4 m[如图(1)].
小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上[如图(2)],墙壁上的影长为1.2 m,落在地面上的影长为2.4 m.
小丽:丙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上[如图(3)],测得第一级台阶上影子长为0.2 m,一级台阶高为0.3 m,落在地面上的影长为4.4 m.
图(1) 图(2) 图(3)
(1)甲树的高度为 m;
(2)求乙树的高度;
(3)选择丙树的高度为 .
A.5.5 m B.5.95 m C.6.05 m D.6.5 m
20.(14分)(2021·江苏扬州邗江区一模)“双十一”期间,某店铺对某品牌玩具推出买一送一活动.已知单个玩具的包装盒为双层上盖的长方体纸箱[上盖纸板面积刚好等于底面面积的2倍,如图(1),纸板厚度都忽略不计].长方体纸箱的长为a cm,宽为b cm,高为c cm.
图(1) 图(2) 图(3)
(1)制作长方体纸箱需要 cm2纸板(请用含有a,b,c的代数式表示);
(2)图(2)为若干玩具包装盒堆成几何体的三视图,则组成这个几何体的玩具个数最少为 个;
(3)由于该店铺在“双十一”期间推出买一送一活动,现要将两个包装好的玩具放在同一个大长方体快递箱内(双层上盖,且上盖朝上,箱内无多余空隙).现有甲、乙两种摆放方式[如图(3)],请分别计算甲、乙两种摆放方式所需快递箱的纸板面积,并比较当b第二十九章 投影与视图
1 2 3 4 5 6 7 8 9 10
B D B B A C C A C A
11.平行 12.圆柱(答案不唯一) 13.变小
14.π 15.x2+3x+2
1.B 皮影、手影、树影都是由光线照射形成的,都是投影,而素描画不是由光线照射形成的,不是投影.故选B.
2.D
3.B
4.B 小明由A处径直走到路灯下方时,他在地上的影子逐渐变短;当他从路灯下方走到B处时,他在地上的影子逐渐变长.故选B.
5.A
6.C
7.C 太阳从东边升起,从西边落下,按照时间的先后顺序排列正确的是(4)(3)(2)(1).故选C.
8.A
图示速解
移动前后的几何体的三视图如下,所以主视图和左视图改变,俯视图不变.故选A.
9.C 综合俯视图和主视图可知,由前向后看,这个几何体的右边一列最多有4个小正方体,中间一列最多有2个小正方体,左边一列最多有4个小正方体,所以组成这个几何体的小正方体的个数最多是10.
10.A 由题图中的三视图知,该几何体是底面半径为4、高为6的圆柱被沿高的方向切掉一个圆柱的几何体,所以其表面积为×2π×4×6+2×4×6+2××π×42
=60π+48.
11.平行 因为太阳光属于平行光线,而日晷利用日影测定时刻,所以晷针在晷面上所形成的投影属于平行投影.
12.圆柱(答案不唯一) 主视图是矩形的立体图形可以是圆柱、长方体等.
13.变小
14.π 由三视图可知,该几何体是由圆柱和圆锥构成,圆柱和圆锥的底面直径均为2,高分别为4和1,∴圆锥和圆柱的底面积为π,该几何体的体积为π+π×1
=π.
15.x2+3x+2 ∵S主视图=x2+2x=x(x+2),S左视图=x2+x=x(x+1),∴俯视图的长为x+2,宽为x+1,则S俯视图=(x+2)(x+1)=x2+3x+2.
16.【参考答案】(1)补全三视图如图所示. (3分)
(2)补全三视图如图所示. (6分)
17.【参考答案】(1)如图,点O为灯泡所在的位置, (2分)
线段FH为小亮在灯光下形成的影子. (5分)
(2)由题意可得,=,
即=,
解得OD=4.
答:灯泡的高为4 m. (10分)
18.【参考答案】(1)2 3 2 6 (8分)
解法提示:如图,过点A作AE⊥BC于点E,
则BE=(7-3)÷2=2.
∵∠B=60°,
∴∠BAE=90°-60°=30°,
∴AB=4,AE=6,
∴a=2,b=3,c=2,d=6.
(2)3×20+4×20×2+7×20
=60+160+140
=360.
故这个直四棱柱的侧面积是360. (12分)
19.【解题思路】(1)根据测得一根长为1 m的竹竿的影长为0.8 m,利用比例式直接得出树高;(2)画出几何图形,把树高分成两个部分,其中一部分等于墙壁上的影长,另一部分利用比例式求出;(3)先求出第一级台阶上影子所对应的树的高度,再求出落在地面上的影子所对应的树的高度,即可得出答案.
【参考答案】(1)5 (3分)
解法提示:设甲树的高度为x m.
根据题意,可得=,
解得x=5.
(2)如图(1),设乙树的高度为AB,则其落在地面上的影长BC=2.4 m,乙树的AE部分的影子落在墙上的DC处,
易知四边形AECD是平行四边形,
∴AE=CD=1.2 m.
由题意,得==,
解得BE=3 m,
故乙树的高度AB=AE+BE=1.2+3=4.2(m). (9分)
图(1)
(3)C(13分)
解法提示:如图(2),设丙树的高度为AB,则丙树上的AG部分落在第一级台阶上的影长EF=0.2 m,
由题意得=,
解得DE=0.25 m,
则CD=0.25+0.3=0.55(m).
易知四边形AGCD是平行四边形,
∴AG=CD=0.55 m,
又由题意得==,
∴BG=5.5 m,
∴AB=AG+BG=0.55+5.5=6.05(m).
图(2)
20.【参考答案】(1)(2ac+2bc+3ab) (3分)
(2)9 (7分)
(3)甲:2(ac+2bc+2ab)+2ab=(2ac+4bc+6ab)cm2,
乙:2(2ab+2ac+bc)+2ab=(4ac+2bc+6ab)cm2. (9分)
甲种摆放方式所需纸板面积-乙种摆放方式所需纸板面积=2ac+4bc+6ab-4ac-2bc-6ab=2c(b-a). (12分)
∵b∴b-a<0,
∴2c(b-a)<0,
∴甲种摆放方式所需快递箱的纸板面积更少. (14分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版九年级数学下学期单元测试卷
第二十九章 投影与视图
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.下列现象不属于投影的是 ( )
A.皮影 B.素描画 C.手影 D.树影
2.(2022·湖北黄冈中考改编)某几何体的三视图如图所示,则该几何体是 ( )
A.圆锥 B.三棱锥 C.四棱柱 D.三棱柱
(第2题) (第3题)
3. (2022·四川成都龙泉驿区模拟)唐代诗人李白《日出行》中有:“日出东方隈,似从地底来.”描述的是看日出的景象,意思是太阳从东方升起,似从地底而来.如图所示,此时观测到地平线和太阳所成的视图可能是 ( )
A B C D
4.(2021·四川成都模拟)如图,晚上小明在路灯下从A处径直走到B处,这一过程中他在地上的影子
( )
A.一直都在变短 B.先变短后变长
C.一直都在变长 D.先变长后变短
5.当某一几何体在投影面P前的摆放位置确定以后,改变它与投影面P的距离,其正投影的形状 ( )
A.不发生变化 B.变大 C.变小 D.无法确定
6.[教材变式P93第5题](2022·北京朝阳区二模)在太阳光的照射下,一个矩形框在水平地面上形成的投影不可能是 ( )
A B C D
7.如图是某公园中的两个物体,一天中四个不同时刻在太阳光的照射下落在地面上的影子,按照时间的先后顺序排列正确的是 ( )
(1) (2) (3) (4)
A.(3)(4)(1)(2) B.(4)(3)(1)(2) C.(4)(3)(2)(1) D.(2)(4)(3)(1)
8.[教材变式P102第6题](2022·河南开封二模)如图是由8个同样大小的小正方体组成的几何体,若将小正方体①正移到小正方体②的上方,则下列说法正确的是 ( )
A.左视图改变,俯视图不变
B.主视图改变,左视图不变
C.主视图与左视图都不变
D.主视图、左视图、俯视图都发生改变
9.(2022·山西大同模拟)由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数最多是 ( )
A.8 B.9 C.10 D.11
10.(2022·四川德阳旌阳区一模)如图是一个几何体的三视图,根据图中提供的数据,可知这个几何体的表面积是 ( )
A.48+60π B.48+40π C.48+30π D.48+36π
二、填空题(共5小题,每小题3分,共15分)
11.(2022·辽宁铁岭模拟)如图,日晷是我国古代利用日影测定时刻的仪器,则晷针在晷面上所形成的投影属于 投影.(填“平行”或“中心”)
12.(2021·北京通州区一模)请写出一个三视图中,主视图是矩形的立体图形: .
13.(2022·陕西咸阳秦都区期末)地面上有一支点燃的蜡烛,蜡烛前面有一面墙,王涛同学在蜡烛与墙之间运动,则他在墙上的投影长度随着他离墙的距离变小
而 (填“增大”或“变小”).
14.[教材变式P110第7题](2021·江西模拟)已知某几何体的三视图如图所示,根据图中数据求得该几何体的体积为 .(结果保留π)
15.(2022·山东枣庄峄城区期末)已知图(2)是图(1)中长方体的三视图,若用S表示面积,S主视图=x2+2x,S左视图=x2+x,则S俯视图= .
图(1) 图(2)
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15.
三、解答题(共5小题,共55分)
16.(6分)添线补全下列三视图.
(1)
(2)
17.(10分)(2021·陕西韩城期末)如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6 m,他的影子长AC=1.4 m,且他到路灯的距离AD=2.1 m,求灯泡的高.
18.(12分)[教材变式P110第7题](2022·辽宁铁岭模拟改编)如图(1)是一个直四棱柱,如图(2)是它的三视图,其俯视图是等腰梯形.
(1)根据图(2)中的数据,可知a= ,b= ,c= ,d= .
(2)请你根据图(1)和问题(1)中的结果,计算这个直四棱柱的侧面积.(结果可保留根号)
图(1) 图(2)
19.(13分)在“测量物体的高度” 活动中,某数学兴趣小组的3名同学选择了测量学校里的3棵树的高度.在同一时刻的阳光下,他们分别做了以下工作:
小芳:测得一根长为1 m的竹竿的影长为0.8 m,甲树的影长为4 m[如图(1)].
小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上[如图(2)],墙壁上的影长为1.2 m,落在地面上的影长为2.4 m.
小丽:丙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上[如图(3)],测得第一级台阶上影子长为0.2 m,一级台阶高为0.3 m,落在地面上的影长为4.4 m.
图(1) 图(2) 图(3)
(1)甲树的高度为 m;
(2)求乙树的高度;
(3)选择丙树的高度为 .
A.5.5 m B.5.95 m C.6.05 m D.6.5 m
20.(14分)(2021·江苏扬州邗江区一模)“双十一”期间,某店铺对某品牌玩具推出买一送一活动.已知单个玩具的包装盒为双层上盖的长方体纸箱[上盖纸板面积刚好等于底面面积的2倍,如图(1),纸板厚度都忽略不计].长方体纸箱的长为a cm,宽为b cm,高为c cm.
图(1) 图(2) 图(3)
(1)制作长方体纸箱需要 cm2纸板(请用含有a,b,c的代数式表示);
(2)图(2)为若干玩具包装盒堆成几何体的三视图,则组成这个几何体的玩具个数最少为 个;
(3)由于该店铺在“双十一”期间推出买一送一活动,现要将两个包装好的玩具放在同一个大长方体快递箱内(双层上盖,且上盖朝上,箱内无多余空隙).现有甲、乙两种摆放方式[如图(3)],请分别计算甲、乙两种摆放方式所需快递箱的纸板面积,并比较当b
1 2 3 4 5 6 7 8 9 10
B D B B A C C A C A
11.平行 12.圆柱(答案不唯一) 13.变小
14.π 15.x2+3x+2
1.B 皮影、手影、树影都是由光线照射形成的,都是投影,而素描画不是由光线照射形成的,不是投影.故选B.
2.D
3.B
4.B 小明由A处径直走到路灯下方时,他在地上的影子逐渐变短;当他从路灯下方走到B处时,他在地上的影子逐渐变长.故选B.
5.A
6.C
7.C 太阳从东边升起,从西边落下,按照时间的先后顺序排列正确的是(4)(3)(2)(1).故选C.
8.A
图示速解
移动前后的几何体的三视图如下,所以主视图和左视图改变,俯视图不变.故选A.
9.C 综合俯视图和主视图可知,由前向后看,这个几何体的右边一列最多有4个小正方体,中间一列最多有2个小正方体,左边一列最多有4个小正方体,所以组成这个几何体的小正方体的个数最多是10.
10.A 由题图中的三视图知,该几何体是底面半径为4、高为6的圆柱被沿高的方向切掉一个圆柱的几何体,所以其表面积为×2π×4×6+2×4×6+2××π×42
=60π+48.
11.平行 因为太阳光属于平行光线,而日晷利用日影测定时刻,所以晷针在晷面上所形成的投影属于平行投影.
12.圆柱(答案不唯一) 主视图是矩形的立体图形可以是圆柱、长方体等.
13.变小
14.π 由三视图可知,该几何体是由圆柱和圆锥构成,圆柱和圆锥的底面直径均为2,高分别为4和1,∴圆锥和圆柱的底面积为π,该几何体的体积为π+π×1
=π.
15.x2+3x+2 ∵S主视图=x2+2x=x(x+2),S左视图=x2+x=x(x+1),∴俯视图的长为x+2,宽为x+1,则S俯视图=(x+2)(x+1)=x2+3x+2.
16.【参考答案】(1)补全三视图如图所示. (3分)
(2)补全三视图如图所示. (6分)
17.【参考答案】(1)如图,点O为灯泡所在的位置, (2分)
线段FH为小亮在灯光下形成的影子. (5分)
(2)由题意可得,=,
即=,
解得OD=4.
答:灯泡的高为4 m. (10分)
18.【参考答案】(1)2 3 2 6 (8分)
解法提示:如图,过点A作AE⊥BC于点E,
则BE=(7-3)÷2=2.
∵∠B=60°,
∴∠BAE=90°-60°=30°,
∴AB=4,AE=6,
∴a=2,b=3,c=2,d=6.
(2)3×20+4×20×2+7×20
=60+160+140
=360.
故这个直四棱柱的侧面积是360. (12分)
19.【解题思路】(1)根据测得一根长为1 m的竹竿的影长为0.8 m,利用比例式直接得出树高;(2)画出几何图形,把树高分成两个部分,其中一部分等于墙壁上的影长,另一部分利用比例式求出;(3)先求出第一级台阶上影子所对应的树的高度,再求出落在地面上的影子所对应的树的高度,即可得出答案.
【参考答案】(1)5 (3分)
解法提示:设甲树的高度为x m.
根据题意,可得=,
解得x=5.
(2)如图(1),设乙树的高度为AB,则其落在地面上的影长BC=2.4 m,乙树的AE部分的影子落在墙上的DC处,
易知四边形AECD是平行四边形,
∴AE=CD=1.2 m.
由题意,得==,
解得BE=3 m,
故乙树的高度AB=AE+BE=1.2+3=4.2(m). (9分)
图(1)
(3)C(13分)
解法提示:如图(2),设丙树的高度为AB,则丙树上的AG部分落在第一级台阶上的影长EF=0.2 m,
由题意得=,
解得DE=0.25 m,
则CD=0.25+0.3=0.55(m).
易知四边形AGCD是平行四边形,
∴AG=CD=0.55 m,
又由题意得==,
∴BG=5.5 m,
∴AB=AG+BG=0.55+5.5=6.05(m).
图(2)
20.【参考答案】(1)(2ac+2bc+3ab) (3分)
(2)9 (7分)
(3)甲:2(ac+2bc+2ab)+2ab=(2ac+4bc+6ab)cm2,
乙:2(2ab+2ac+bc)+2ab=(4ac+2bc+6ab)cm2. (9分)
甲种摆放方式所需纸板面积-乙种摆放方式所需纸板面积=2ac+4bc+6ab-4ac-2bc-6ab=2c(b-a). (12分)
∵b
∴2c(b-a)<0,
∴甲种摆放方式所需快递箱的纸板面积更少. (14分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
