2024人教版九年级数学下学期单元测试卷--期中综合测试卷(含答案)
文档属性
| 名称 | 2024人教版九年级数学下学期单元测试卷--期中综合测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024人教版九年级数学下学期单元测试卷
期中综合能力测评卷
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.若反比例函数y=(k≠0)的图象过点(1,),则该函数的图象位于 ( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
2.已知y=(m-2)是反比例函数,则m的值为 ( )
A.2 B.-2 C.±2 D.任意实数
3.如图,是某位同学用带有刻度的直尺在数轴上作图的方法,若图中的虚线相互平行,则点P表示的数是 ( )
A.1 B. C. D.5
(第3题) (第4题)
4.如图,在 ABCD中,E是AD的中点,EC交对角线BD于点F,则= ( )
A. B.2 C. D.
5.已知正比例函数y1=kx的图象与反比例函数y2=的图象相交于点A(2,4),则下列说法正确的是 ( )
A.y1与y2都随x的增大而增大
B.两个函数图象的另一交点坐标为(2,-4)
C.当x<-2或0D.反比例函数的解析式是y2=-
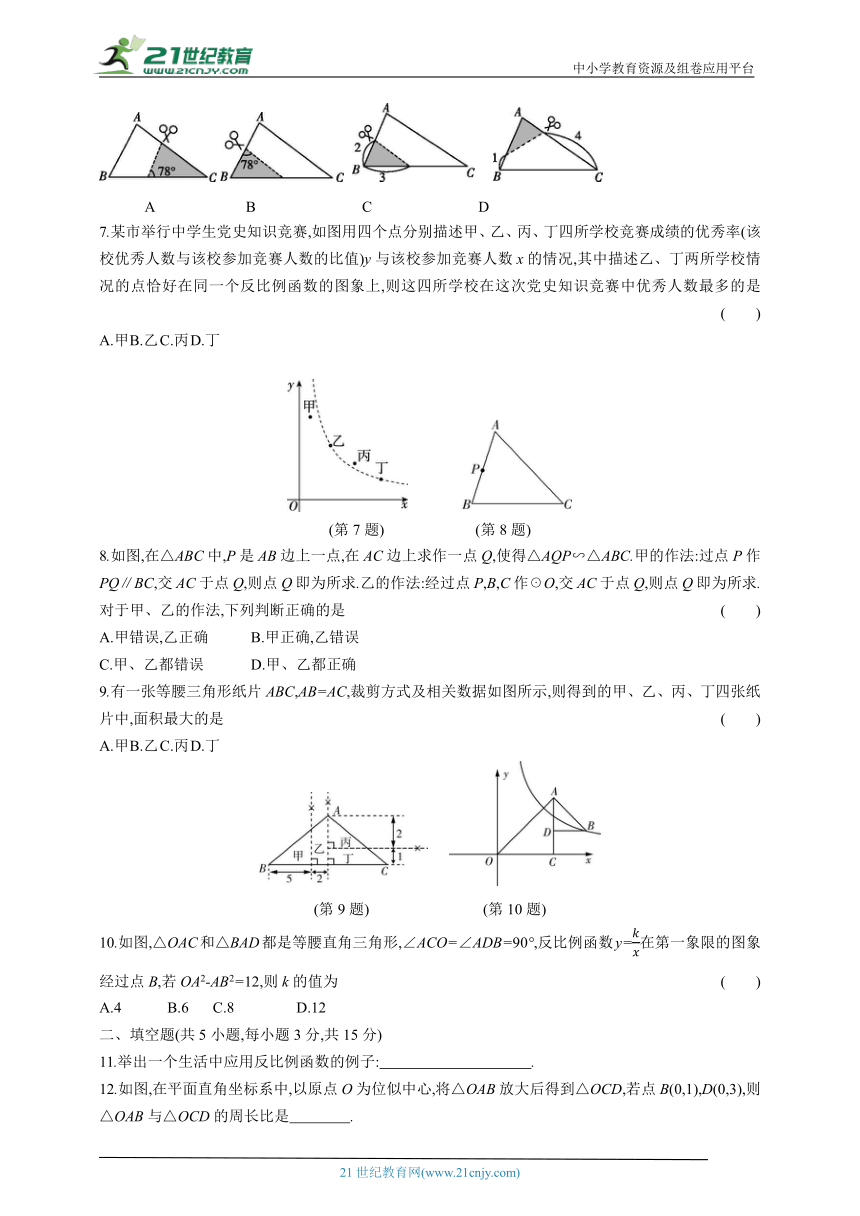
6.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不一定相似的是 ( )
A B C D
7.某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次党史知识竞赛中优秀人数最多的是 ( )
A.甲 B.乙 C.丙 D.丁
(第7题) (第8题)
8.如图,在△ABC中,P是AB边上一点,在AC边上求作一点Q,使得△AQP∽△ABC.甲的作法:过点P作PQ∥BC,交AC于点Q,则点Q即为所求.乙的作法:经过点P,B,C作☉O,交AC于点Q,则点Q即为所求.对于甲、乙的作法,下列判断正确的是 ( )
A.甲错误,乙正确 B.甲正确,乙错误
C.甲、乙都错误 D.甲、乙都正确
9.有一张等腰三角形纸片ABC,AB=AC,裁剪方式及相关数据如图所示,则得到的甲、乙、丙、丁四张纸片中,面积最大的是 ( )
A.甲 B.乙 C.丙 D.丁
(第9题) (第10题)
10.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,若OA2-AB2=12,则k的值为 ( )
A.4 B.6 C.8 D.12
二、填空题(共5小题,每小题3分,共15分)
11.举出一个生活中应用反比例函数的例子: .
12.如图,在平面直角坐标系中,以原点O为位似中心,将△OAB放大后得到△OCD,若点B(0,1),D(0,3),则△OAB与△OCD的周长比是 .
(第12题) (第13题)
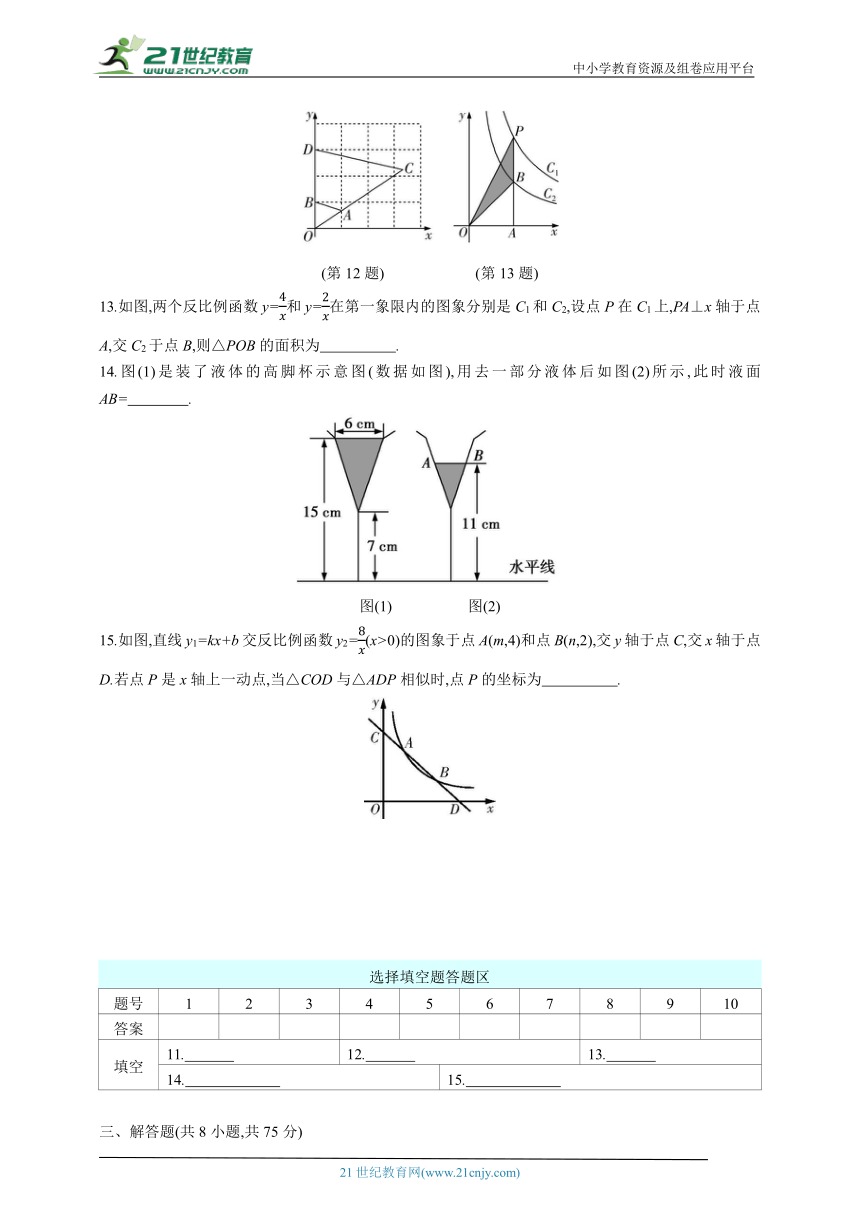
13.如图,两个反比例函数y=和y=在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为 .
14.图(1)是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图(2)所示,此时液面AB= .
图(1) 图(2)
15.如图,直线y1=kx+b交反比例函数y2=(x>0)的图象于点A(m,4)和点B(n,2),交y轴于点C,交x轴于点D.若点P是x轴上一动点,当△COD与△ADP相似时,点P的坐标为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15.
三、解答题(共8小题,共75分)
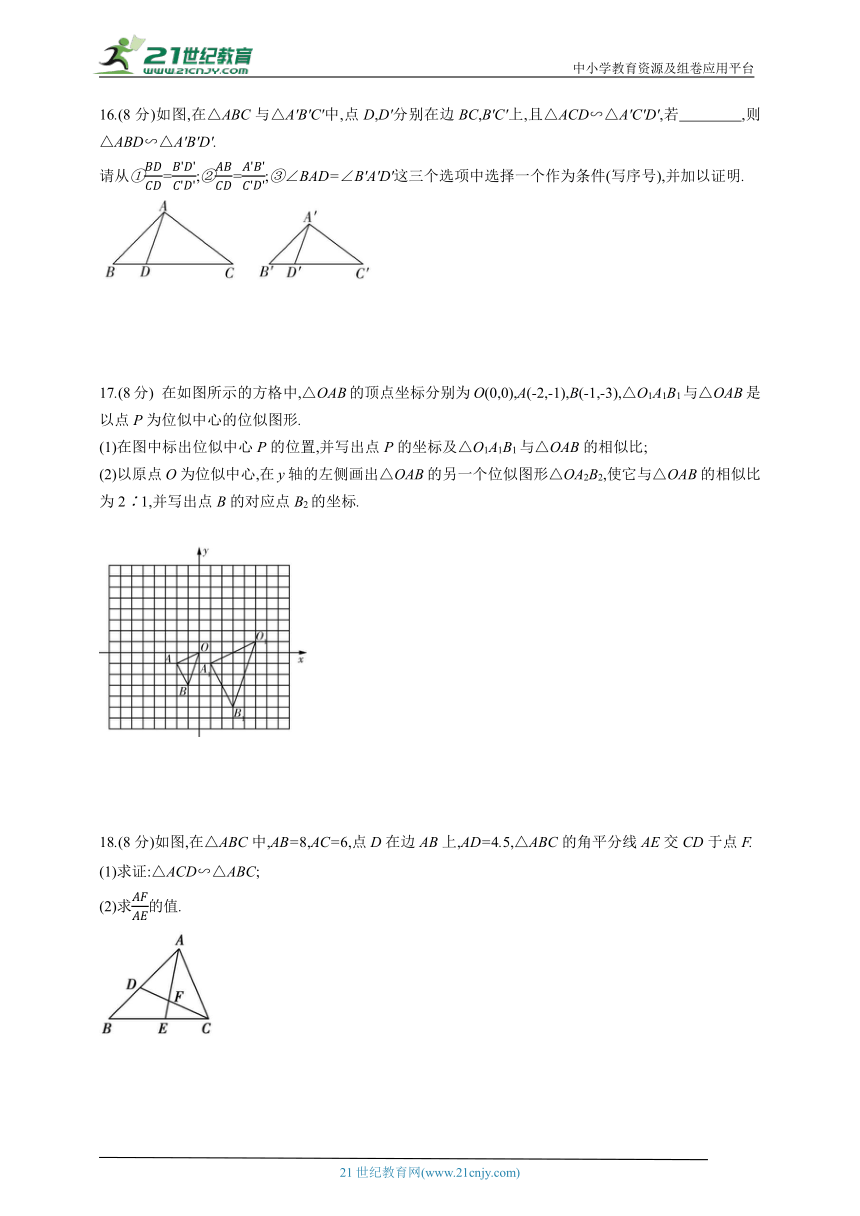
16.(8分)如图,在△ABC与△A'B'C'中,点D,D'分别在边BC,B'C'上,且△ACD∽△A'C'D',若 ,则△ABD∽△A'B'D'.
请从①=;②=;③∠BAD=∠B'A'D'这三个选项中选择一个作为条件(写序号),并加以证明.
17.(8分) 在如图所示的方格中,△OAB的顶点坐标分别为O(0,0),A(-2,-1),B(-1,-3),△O1A1B1与△OAB是以点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点P的坐标及△O1A1B1与△OAB的相似比;
(2)以原点O为位似中心,在y轴的左侧画出△OAB的另一个位似图形△OA2B2,使它与△OAB的相似比为2∶1,并写出点B的对应点B2的坐标.
18.(8分)如图,在△ABC中,AB=8,AC=6,点D在边AB上,AD=4.5,△ABC的角平分线AE交CD于点F.
(1)求证:△ACD∽△ABC;
(2)求的值.
19.(9分)如图,已知反比例函数y= 与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4).
(1)求点A的坐标;
(2)求出这两个函数图象的另一个交点B的坐标,及△AOB的面积;
(3)根据图象直接写出反比例函数值大于一次函数值的x的取值范围.
20.(9分)一辆客车从甲地出发前往乙地,平均速度v(km/h)与所用时间t(h)之间的函数关系如图所示,其中60≤v≤120.
(1)求v关于t的函数解析式.
(2)客车上午8:00从甲地出发.
①客车需在当天14:40至15:30(含14:40和15:30)间到达乙地,求客车行驶的平均速度v的范围;
②客车能否在当天12:30前到达乙地 说明理由.
21.(10分)如图,在平面直角坐标系中,平行四边形ABCD的边AB在x轴上,点D在反比例函数y=(k≠0,x>0)的图象上,已知点C的坐标为(12,8),平行四边形ABCD的面积为64.
(1)求k的值;
(2)若点E为反比例函数y=(k≠0,x>0)的图象与BC边的交点,且=,求点E的坐标.
22.(11分)背景:点A在反比例函数y=(k>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,分别在射线AC,BO上取点D,E,使得四边形ABED为正方形.如图(1),点A在第一象限,当AC=4时,小李测得CD=3.
探究:通过改变点A的位置,小李发现点D,A的横坐标之间存在函数关系,请帮助小李解决下列问题.
(1)求反比例函数的解析式.
(2)设点A,D的横坐标分别为x,z,将z关于x的函数称为“Z函数”,如图(2),小李画出了当x>0时,“Z函数”的图象.
①求这个“Z函数”的解析式.
②补画当x<0时,“Z函数”的图象.
③若y=-x与“Z函数”相交于A,B两点,则A,B两点横坐标之间的距离是 .
23.(12分)如图所示,点A,C在BD的同侧,AB⊥BD于点B,CD⊥BD于点D,E,F是直线BD上的两点,AE交CF于点H,且HP⊥BD于点P.已知AB=CD=10,HP=3,BD=12.
(1)当点P在线段BD上时(B,D两点除外),如图(1).
①若BP=6,求PE的长.
②试猜想EF的长是一个确定的值吗 如果是,请将这个值求出来;如果不是,请说明理由.
(2)若点P是BD延长线上任意一点,如图(2),EF的长与(1)中相同吗 如果相同,请说明理由;如果不同,求EF的长.
图(1) 图(2)
九年级下册期中综合能力测评卷
1 2 3 4 5 6 7 8 9 10
B B D A C C C A D B
11.要编织一块面积为2米2的矩形地毯,地毯的长x(米)与宽y(米)之间的函数解析式为y=(x>0)(答案不唯一)
12.1∶3 13.1 14.3 cm 15.(2,0)或(-2,0)
1.B 由题意得k=>0,∴该函数的图象位于第一、三象限.
2.B ∵y=(m-2)是反比例函数,∴解得m=-2.
3.D 如图,OB=1.5,OA=3,OC=10,∵PB∥AC,∴=,∴=,∴OP=5,∴点P表示的数是5.
4.A ∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴△EDF∽△CBF,∴=.∵E是AD的中点,∴DE=AD,∴==,∴=.
5.C ∵正比例函数y1=kx的图象与反比例函数y2=的图象相交于点A(2,4),∴正比例函数的解析式为y1=2x,反比例函数的解析式为y2=,∴y1随x的增大而增大,y2在每个象限内,随x的增大而减小.两个函数图象的另一个交点坐标为(-2,-4).∵当x<-2或06.C 选项A中,阴影三角形与原三角形有两个角相等,故两三角形相似;选项B中,阴影三角形与原三角形有两个角相等,故两三角形相似;选项C中,阴影三角形与原三角形有两边成比例,但成比例的两边的夹角不一定相等,故两三角形不一定相似;选项D中,阴影三角形与原三角形的两边成比例且夹角相等,故两三角形相似.故选C.
7.C 根据题意可知,xy的值表示优秀人数.∵描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,∴乙、丁两所学校的优秀人数相同.∵描述丙学校情况的点在反比例函数图象的上方,∴丙校的xy的值最大,即优秀人数最多.故选C.
8.A
图示速解 如图(1),∵PQ∥BC,∴△AQP∽△ACB,∴甲的作法错误.如图(2),∵B,C,Q,P四点共圆,
∴∠B+∠CQP=180°.∵∠AQP+∠CQP=180°,∴∠AQP=∠B.∵∠A=∠A,∴△AQP∽△ABC,∴乙的作法正确.故选A.
9.D 如图,∵AD⊥BC,AB=AC,∴CD=BD=5+2=7.∵AD=2+1=3,∴S△ABD=S△ACD=×7×3=.
∵EF∥AD,∴△EBF∽△ABD,∴=()2=,∴S甲=,∴S乙=-=.同理可得=()2=,∴S丙=,∴S丁=-=.∵>>>,∴面积最大的是丁.
一题多解 如图,∵△ABC是等腰三角形,AD⊥BC,∴S△ABD=S△ACD.∵EF∥AD,MN∥BC,∴△EBF∽△ABD,
△AMN∽△ADC.∵=()2=,∴=1-=.∵=()2=,∴=1-=.∵>>>,
∴S丁>S甲>S乙>S丙,∴面积最大的是丁.
10.B 设B点坐标为(a,b),因为△OAC和△BAD都是等腰直角三角形,所以OA= AC,AB=AD,OC=AC,AD=BD.由于OA2-AB2=12,则(AC)2-(AD)2=12,化简得AC2-AD2=6,即(AC+AD)(AC-AD)=6,所以(OC+BD)·CD=6,从而a·b=6,所以反比例函数y=中k=6.故选B.
11.要编织一块面积为2米2的矩形地毯,地毯的长x(米)与宽y(米)之间的函数解析式为y=(x>0)(答案不唯一)
12.1∶3 ∵点B(0,1),D(0,3),∴OB=1,OD=3.∵△OAB与△OCD位似,∴△OAB∽△OCD,
∴△OAB与△OCD的相似比是OB∶OD=1∶3,∴△OAB与△OCD的周长比是1∶3.
13.1 ∵PA⊥x轴于点A,交C2于点B,∴S△POA=×4=2,S△BOA=×2=1,
∴S△POB=S△POA-S△BOA=2-1=1.
14.3 cm 如图,过点O作OM⊥CD,垂足为M,过点O作ON⊥AB,垂足为N,∵CD∥AB,
∴△CDO∽△ABO,即相似比为,∴=.∵OM=15-7=8(cm),ON=11-7=4(cm),
∴=,∴AB=3 cm.
15.(2,0)或(-2,0) (分类讨论思想)∵点A(m,4)和点B(n,2)在反比例函数y2=(x>0)的图象上,∴4=,2=,解得m=2,n=4,∴A(2,4),B(4,2).把A(2,4),B(4,2)代入直线y1=kx+b,得解得∴y1=-x+6.当x=0时,y1=6,∴C(0,6),∴OC=6.当y1=0时,x=6,
∴D(6,0),∴OD=6,∴CD==6.易得AD=4.设P(a,0),由题可知,点P在点D的左侧,则PD=6-a.①当△COD∽△APD时,=,即=,解得a=2,故P(2,0).②当△COD∽△PAD时,=,即=,解得a=-2,故P(-2,0).∴当△COD与△ADP相似时,点P的坐标为(2,0)或(-2,0).
16.【参考答案】选择③. (2分)
证明:∵△ACD∽△A'C'D',
∴∠ADC=∠A'D'C',
∴∠ADB=∠A'D'B'.
又∠BAD=∠B'A'D',
∴△ABD∽△A'B'D'. (8分)
一题多解
选择①. (2分)
证明:∵△ACD∽△A'C'D' ,
∴= ,∠ADC=∠A'D'C',
∴∠ADB=∠A'D'B'.
又=,
∴==,
∴=.
又∠ADB=∠A'D'B',
∴△ABD∽△A'B'D'. (8分)
高分锦囊 证明两个三角形相似的几种思路
(1)有平行截线——用平行线的性质找“等角”.
(2)有一对等角——找“另一对等角”或“夹边对应成比例”.
(3)有两边对应成比例——找“夹角相等”或“第三边也对应成比例”.
(4)直角三角形——找“一对锐角相等”或“两直角边对应成比例”.
(5)等腰三角形——找“顶角相等”或“一对底角相等”或“底和腰对应成比例”.
17.【参考答案】(1)如图所示.P(-5,-1). (2分)
△O1A1B1与△OAB的相似比等于2∶1. (4分)
(2)如图所示,△OA2B2即为所求.
(6分)
点B2的坐标为(-2,-6). (8分)
18.【参考答案】(1)证明:∵AB=8,AC=6,AD=4.5,
∴==.
又∠CAD=∠BAC,
∴△ACD∽△ABC. (5分)
(2)由(1)知,△ACD∽△ABC,
∴∠ACD=∠B.
∵AE平分∠BAC,
∴∠CAF=∠BAE,
∴△ACF∽△ABE,
∴==. (8分)
19.【参考答案】(1)∵反比例函数y=的图象与一次函数y=x+b的图象在第一象限交于点A(1,-k+4),
∴-k+4=,解得k=2. (2分)
∴点A的坐标为(1,2). (3分)
(2)将点A的坐标(1,2)代入y=x+b,得2=1+b,
解得b=1,
∴一次函数的解析式为y=x+1.
由(1)得,反比例函数的解析式为y=.
联立两函数解析式,得
解得或
则这两个函数图象的另一个交点B的坐标是(-2,-1). (5分)
设直线y=x+1与x轴交于点C.
把y=0代入y=x+1中,解得x=-1,则C(-1,0),
∴OC=1, ( 6分)
∴S△AOB=S△AOC+S△BOC=+=,
即△AOB的面积是. (7分)
(3)观察图象知反比例函数值大于一次函数值时,x的取值范围是x<-2或0高分锦囊 一次函数与反比例函数综合题的解题通法
(1)求函数表达式:一般通过其中一个函数表达式得到交点坐标,再代入另一函数表达式求解即可.
(2)求两函数图象的交点坐标:联立一次函数与反比例函数的表达式,求解即可.
(3)求三角形的面积:当三角形有一边在坐标轴上或与坐标轴平行时,通常作该边上的高,再利用面积公式求解;当三边均不在坐标轴上且均不与坐标轴平行时,通常采用“S=×铅垂高×水平宽”来求解.
(4)比较两函数值的大小,求自变量的取值范围:找到交点后结合函数图象解答.
20.【参考答案】(1)设v关于t的函数解析式为v=,
将(5,120)代入v=,得120=,
解得k=600,
∴v关于t的函数解析式为v=(5≤t≤10). (4分)
(2)①当14:40到达乙地时,
t=,v==600÷=90(km/h);
当15:30到达乙地时,
t=,v==600÷=80(km/h).
∴客车行驶的平均速度v的范围为80≤v≤90. (7分)
②若客车在当天12:30到达时,t=4.5,
此时v==>120,
故客车不能在当天12:30前到达乙地. (9分)
21.【参考答案】(1)如图(1),过点D作DF⊥x轴,垂足为F,
∵四边形ABCD是平行四边形,点C的坐标为(12,8),
∴DF=8.
∵平行四边形ABCD的面积为64,
∴DF·DC=64,
∴DC=8,
∴OF=4,
∴D(4,8).
把点D(4,8)代入y=中,
得8=,
∴k=32. (5分)
(2)如图(2),过点E作NM∥DF,分别交DC,AB延长线于点N,M,
∵四边形ABCD是平行四边形,
∴AB∥CD,MN=DF=8,
∴易得△MEB∽△NEC,
∴==.
设ME=3x,NE=5x,
则MN=ME+NE=3x+5x=8,
∴x=1,
∴ME=3.
由(1)得,反比例函数的解析式为y=(x>0),
∴令y=3,即=3,
∴x=,
∴点E的坐标为(,3). (10分)
22.【参考答案】(1)∵当AC=4时,CD=3,
∴AD=1.
∵四边形ABED是正方形,
∴AB=AD=1,
∴A(4,1).
∵点A在反比例函数y=(k>0)的图象上,
∴k=4×1=4,
∴反比例函数的解析式为y=. (3分)
(2)①由题意知,点A(x,x-z),
∴x(x-z)=4,
∴z=x-. (5分)
②如图所示. (9分)
②2 (11分)
解法提示:令-x=x-,解得x=±,
∴-(-)=2.
23.【解题思路】(1)①根据题中条件,可以证明△HPE∽△ABE,利用相似三角形的性质即可求出PE的长;②由①可知,=,由此可得BE与PE的数量关系,同理可得PF与DF的数量关系,由EF=PE+PF,通过等量代换,可得到关于EF的方程,解方程即可得出答案.(2)根据(1)中的解题思路,同理可得答案.
【参考答案】(1)①∵AB⊥BD,HP⊥BD,
∴AB∥HP,
∴△HPE∽△ABE.
∴=. (2分)
∵AB=10,HP=3,BP=6,
∴=,
解得PE=. (4分)
②EF的长是一个确定的值. (5分)
由①知,==,
∴PE=BE.
同理可得PF=FD. (6分)
∴EF=PE+PF
=BE+FD
=(BE+FD)
=(12+EF),
解得EF=. (7分)
∴EF的长是一个确定的值,其值为. (8分)
(2)相同.
理由:∵AB∥HP,
∴△HPE∽△ABE,
∴==,
∴PE=BE.
同理可得PF=FD. (10分)
∴EF=PE-PF
=BE-FD
=(BE-FD)
=(12+EF),
解得EF=.
∴EF的长与(1)中相同. (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版九年级数学下学期单元测试卷
期中综合能力测评卷
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.若反比例函数y=(k≠0)的图象过点(1,),则该函数的图象位于 ( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
2.已知y=(m-2)是反比例函数,则m的值为 ( )
A.2 B.-2 C.±2 D.任意实数
3.如图,是某位同学用带有刻度的直尺在数轴上作图的方法,若图中的虚线相互平行,则点P表示的数是 ( )
A.1 B. C. D.5
(第3题) (第4题)
4.如图,在 ABCD中,E是AD的中点,EC交对角线BD于点F,则= ( )
A. B.2 C. D.
5.已知正比例函数y1=kx的图象与反比例函数y2=的图象相交于点A(2,4),则下列说法正确的是 ( )
A.y1与y2都随x的增大而增大
B.两个函数图象的另一交点坐标为(2,-4)
C.当x<-2或0
6.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不一定相似的是 ( )
A B C D
7.某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次党史知识竞赛中优秀人数最多的是 ( )
A.甲 B.乙 C.丙 D.丁
(第7题) (第8题)
8.如图,在△ABC中,P是AB边上一点,在AC边上求作一点Q,使得△AQP∽△ABC.甲的作法:过点P作PQ∥BC,交AC于点Q,则点Q即为所求.乙的作法:经过点P,B,C作☉O,交AC于点Q,则点Q即为所求.对于甲、乙的作法,下列判断正确的是 ( )
A.甲错误,乙正确 B.甲正确,乙错误
C.甲、乙都错误 D.甲、乙都正确
9.有一张等腰三角形纸片ABC,AB=AC,裁剪方式及相关数据如图所示,则得到的甲、乙、丙、丁四张纸片中,面积最大的是 ( )
A.甲 B.乙 C.丙 D.丁
(第9题) (第10题)
10.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,若OA2-AB2=12,则k的值为 ( )
A.4 B.6 C.8 D.12
二、填空题(共5小题,每小题3分,共15分)
11.举出一个生活中应用反比例函数的例子: .
12.如图,在平面直角坐标系中,以原点O为位似中心,将△OAB放大后得到△OCD,若点B(0,1),D(0,3),则△OAB与△OCD的周长比是 .
(第12题) (第13题)
13.如图,两个反比例函数y=和y=在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为 .
14.图(1)是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图(2)所示,此时液面AB= .
图(1) 图(2)
15.如图,直线y1=kx+b交反比例函数y2=(x>0)的图象于点A(m,4)和点B(n,2),交y轴于点C,交x轴于点D.若点P是x轴上一动点,当△COD与△ADP相似时,点P的坐标为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15.
三、解答题(共8小题,共75分)
16.(8分)如图,在△ABC与△A'B'C'中,点D,D'分别在边BC,B'C'上,且△ACD∽△A'C'D',若 ,则△ABD∽△A'B'D'.
请从①=;②=;③∠BAD=∠B'A'D'这三个选项中选择一个作为条件(写序号),并加以证明.
17.(8分) 在如图所示的方格中,△OAB的顶点坐标分别为O(0,0),A(-2,-1),B(-1,-3),△O1A1B1与△OAB是以点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点P的坐标及△O1A1B1与△OAB的相似比;
(2)以原点O为位似中心,在y轴的左侧画出△OAB的另一个位似图形△OA2B2,使它与△OAB的相似比为2∶1,并写出点B的对应点B2的坐标.
18.(8分)如图,在△ABC中,AB=8,AC=6,点D在边AB上,AD=4.5,△ABC的角平分线AE交CD于点F.
(1)求证:△ACD∽△ABC;
(2)求的值.
19.(9分)如图,已知反比例函数y= 与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4).
(1)求点A的坐标;
(2)求出这两个函数图象的另一个交点B的坐标,及△AOB的面积;
(3)根据图象直接写出反比例函数值大于一次函数值的x的取值范围.
20.(9分)一辆客车从甲地出发前往乙地,平均速度v(km/h)与所用时间t(h)之间的函数关系如图所示,其中60≤v≤120.
(1)求v关于t的函数解析式.
(2)客车上午8:00从甲地出发.
①客车需在当天14:40至15:30(含14:40和15:30)间到达乙地,求客车行驶的平均速度v的范围;
②客车能否在当天12:30前到达乙地 说明理由.
21.(10分)如图,在平面直角坐标系中,平行四边形ABCD的边AB在x轴上,点D在反比例函数y=(k≠0,x>0)的图象上,已知点C的坐标为(12,8),平行四边形ABCD的面积为64.
(1)求k的值;
(2)若点E为反比例函数y=(k≠0,x>0)的图象与BC边的交点,且=,求点E的坐标.
22.(11分)背景:点A在反比例函数y=(k>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,分别在射线AC,BO上取点D,E,使得四边形ABED为正方形.如图(1),点A在第一象限,当AC=4时,小李测得CD=3.
探究:通过改变点A的位置,小李发现点D,A的横坐标之间存在函数关系,请帮助小李解决下列问题.
(1)求反比例函数的解析式.
(2)设点A,D的横坐标分别为x,z,将z关于x的函数称为“Z函数”,如图(2),小李画出了当x>0时,“Z函数”的图象.
①求这个“Z函数”的解析式.
②补画当x<0时,“Z函数”的图象.
③若y=-x与“Z函数”相交于A,B两点,则A,B两点横坐标之间的距离是 .
23.(12分)如图所示,点A,C在BD的同侧,AB⊥BD于点B,CD⊥BD于点D,E,F是直线BD上的两点,AE交CF于点H,且HP⊥BD于点P.已知AB=CD=10,HP=3,BD=12.
(1)当点P在线段BD上时(B,D两点除外),如图(1).
①若BP=6,求PE的长.
②试猜想EF的长是一个确定的值吗 如果是,请将这个值求出来;如果不是,请说明理由.
(2)若点P是BD延长线上任意一点,如图(2),EF的长与(1)中相同吗 如果相同,请说明理由;如果不同,求EF的长.
图(1) 图(2)
九年级下册期中综合能力测评卷
1 2 3 4 5 6 7 8 9 10
B B D A C C C A D B
11.要编织一块面积为2米2的矩形地毯,地毯的长x(米)与宽y(米)之间的函数解析式为y=(x>0)(答案不唯一)
12.1∶3 13.1 14.3 cm 15.(2,0)或(-2,0)
1.B 由题意得k=>0,∴该函数的图象位于第一、三象限.
2.B ∵y=(m-2)是反比例函数,∴解得m=-2.
3.D 如图,OB=1.5,OA=3,OC=10,∵PB∥AC,∴=,∴=,∴OP=5,∴点P表示的数是5.
4.A ∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴△EDF∽△CBF,∴=.∵E是AD的中点,∴DE=AD,∴==,∴=.
5.C ∵正比例函数y1=kx的图象与反比例函数y2=的图象相交于点A(2,4),∴正比例函数的解析式为y1=2x,反比例函数的解析式为y2=,∴y1随x的增大而增大,y2在每个象限内,随x的增大而减小.两个函数图象的另一个交点坐标为(-2,-4).∵当x<-2或0
7.C 根据题意可知,xy的值表示优秀人数.∵描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,∴乙、丁两所学校的优秀人数相同.∵描述丙学校情况的点在反比例函数图象的上方,∴丙校的xy的值最大,即优秀人数最多.故选C.
8.A
图示速解 如图(1),∵PQ∥BC,∴△AQP∽△ACB,∴甲的作法错误.如图(2),∵B,C,Q,P四点共圆,
∴∠B+∠CQP=180°.∵∠AQP+∠CQP=180°,∴∠AQP=∠B.∵∠A=∠A,∴△AQP∽△ABC,∴乙的作法正确.故选A.
9.D 如图,∵AD⊥BC,AB=AC,∴CD=BD=5+2=7.∵AD=2+1=3,∴S△ABD=S△ACD=×7×3=.
∵EF∥AD,∴△EBF∽△ABD,∴=()2=,∴S甲=,∴S乙=-=.同理可得=()2=,∴S丙=,∴S丁=-=.∵>>>,∴面积最大的是丁.
一题多解 如图,∵△ABC是等腰三角形,AD⊥BC,∴S△ABD=S△ACD.∵EF∥AD,MN∥BC,∴△EBF∽△ABD,
△AMN∽△ADC.∵=()2=,∴=1-=.∵=()2=,∴=1-=.∵>>>,
∴S丁>S甲>S乙>S丙,∴面积最大的是丁.
10.B 设B点坐标为(a,b),因为△OAC和△BAD都是等腰直角三角形,所以OA= AC,AB=AD,OC=AC,AD=BD.由于OA2-AB2=12,则(AC)2-(AD)2=12,化简得AC2-AD2=6,即(AC+AD)(AC-AD)=6,所以(OC+BD)·CD=6,从而a·b=6,所以反比例函数y=中k=6.故选B.
11.要编织一块面积为2米2的矩形地毯,地毯的长x(米)与宽y(米)之间的函数解析式为y=(x>0)(答案不唯一)
12.1∶3 ∵点B(0,1),D(0,3),∴OB=1,OD=3.∵△OAB与△OCD位似,∴△OAB∽△OCD,
∴△OAB与△OCD的相似比是OB∶OD=1∶3,∴△OAB与△OCD的周长比是1∶3.
13.1 ∵PA⊥x轴于点A,交C2于点B,∴S△POA=×4=2,S△BOA=×2=1,
∴S△POB=S△POA-S△BOA=2-1=1.
14.3 cm 如图,过点O作OM⊥CD,垂足为M,过点O作ON⊥AB,垂足为N,∵CD∥AB,
∴△CDO∽△ABO,即相似比为,∴=.∵OM=15-7=8(cm),ON=11-7=4(cm),
∴=,∴AB=3 cm.
15.(2,0)或(-2,0) (分类讨论思想)∵点A(m,4)和点B(n,2)在反比例函数y2=(x>0)的图象上,∴4=,2=,解得m=2,n=4,∴A(2,4),B(4,2).把A(2,4),B(4,2)代入直线y1=kx+b,得解得∴y1=-x+6.当x=0时,y1=6,∴C(0,6),∴OC=6.当y1=0时,x=6,
∴D(6,0),∴OD=6,∴CD==6.易得AD=4.设P(a,0),由题可知,点P在点D的左侧,则PD=6-a.①当△COD∽△APD时,=,即=,解得a=2,故P(2,0).②当△COD∽△PAD时,=,即=,解得a=-2,故P(-2,0).∴当△COD与△ADP相似时,点P的坐标为(2,0)或(-2,0).
16.【参考答案】选择③. (2分)
证明:∵△ACD∽△A'C'D',
∴∠ADC=∠A'D'C',
∴∠ADB=∠A'D'B'.
又∠BAD=∠B'A'D',
∴△ABD∽△A'B'D'. (8分)
一题多解
选择①. (2分)
证明:∵△ACD∽△A'C'D' ,
∴= ,∠ADC=∠A'D'C',
∴∠ADB=∠A'D'B'.
又=,
∴==,
∴=.
又∠ADB=∠A'D'B',
∴△ABD∽△A'B'D'. (8分)
高分锦囊 证明两个三角形相似的几种思路
(1)有平行截线——用平行线的性质找“等角”.
(2)有一对等角——找“另一对等角”或“夹边对应成比例”.
(3)有两边对应成比例——找“夹角相等”或“第三边也对应成比例”.
(4)直角三角形——找“一对锐角相等”或“两直角边对应成比例”.
(5)等腰三角形——找“顶角相等”或“一对底角相等”或“底和腰对应成比例”.
17.【参考答案】(1)如图所示.P(-5,-1). (2分)
△O1A1B1与△OAB的相似比等于2∶1. (4分)
(2)如图所示,△OA2B2即为所求.
(6分)
点B2的坐标为(-2,-6). (8分)
18.【参考答案】(1)证明:∵AB=8,AC=6,AD=4.5,
∴==.
又∠CAD=∠BAC,
∴△ACD∽△ABC. (5分)
(2)由(1)知,△ACD∽△ABC,
∴∠ACD=∠B.
∵AE平分∠BAC,
∴∠CAF=∠BAE,
∴△ACF∽△ABE,
∴==. (8分)
19.【参考答案】(1)∵反比例函数y=的图象与一次函数y=x+b的图象在第一象限交于点A(1,-k+4),
∴-k+4=,解得k=2. (2分)
∴点A的坐标为(1,2). (3分)
(2)将点A的坐标(1,2)代入y=x+b,得2=1+b,
解得b=1,
∴一次函数的解析式为y=x+1.
由(1)得,反比例函数的解析式为y=.
联立两函数解析式,得
解得或
则这两个函数图象的另一个交点B的坐标是(-2,-1). (5分)
设直线y=x+1与x轴交于点C.
把y=0代入y=x+1中,解得x=-1,则C(-1,0),
∴OC=1, ( 6分)
∴S△AOB=S△AOC+S△BOC=+=,
即△AOB的面积是. (7分)
(3)观察图象知反比例函数值大于一次函数值时,x的取值范围是x<-2或0
(1)求函数表达式:一般通过其中一个函数表达式得到交点坐标,再代入另一函数表达式求解即可.
(2)求两函数图象的交点坐标:联立一次函数与反比例函数的表达式,求解即可.
(3)求三角形的面积:当三角形有一边在坐标轴上或与坐标轴平行时,通常作该边上的高,再利用面积公式求解;当三边均不在坐标轴上且均不与坐标轴平行时,通常采用“S=×铅垂高×水平宽”来求解.
(4)比较两函数值的大小,求自变量的取值范围:找到交点后结合函数图象解答.
20.【参考答案】(1)设v关于t的函数解析式为v=,
将(5,120)代入v=,得120=,
解得k=600,
∴v关于t的函数解析式为v=(5≤t≤10). (4分)
(2)①当14:40到达乙地时,
t=,v==600÷=90(km/h);
当15:30到达乙地时,
t=,v==600÷=80(km/h).
∴客车行驶的平均速度v的范围为80≤v≤90. (7分)
②若客车在当天12:30到达时,t=4.5,
此时v==>120,
故客车不能在当天12:30前到达乙地. (9分)
21.【参考答案】(1)如图(1),过点D作DF⊥x轴,垂足为F,
∵四边形ABCD是平行四边形,点C的坐标为(12,8),
∴DF=8.
∵平行四边形ABCD的面积为64,
∴DF·DC=64,
∴DC=8,
∴OF=4,
∴D(4,8).
把点D(4,8)代入y=中,
得8=,
∴k=32. (5分)
(2)如图(2),过点E作NM∥DF,分别交DC,AB延长线于点N,M,
∵四边形ABCD是平行四边形,
∴AB∥CD,MN=DF=8,
∴易得△MEB∽△NEC,
∴==.
设ME=3x,NE=5x,
则MN=ME+NE=3x+5x=8,
∴x=1,
∴ME=3.
由(1)得,反比例函数的解析式为y=(x>0),
∴令y=3,即=3,
∴x=,
∴点E的坐标为(,3). (10分)
22.【参考答案】(1)∵当AC=4时,CD=3,
∴AD=1.
∵四边形ABED是正方形,
∴AB=AD=1,
∴A(4,1).
∵点A在反比例函数y=(k>0)的图象上,
∴k=4×1=4,
∴反比例函数的解析式为y=. (3分)
(2)①由题意知,点A(x,x-z),
∴x(x-z)=4,
∴z=x-. (5分)
②如图所示. (9分)
②2 (11分)
解法提示:令-x=x-,解得x=±,
∴-(-)=2.
23.【解题思路】(1)①根据题中条件,可以证明△HPE∽△ABE,利用相似三角形的性质即可求出PE的长;②由①可知,=,由此可得BE与PE的数量关系,同理可得PF与DF的数量关系,由EF=PE+PF,通过等量代换,可得到关于EF的方程,解方程即可得出答案.(2)根据(1)中的解题思路,同理可得答案.
【参考答案】(1)①∵AB⊥BD,HP⊥BD,
∴AB∥HP,
∴△HPE∽△ABE.
∴=. (2分)
∵AB=10,HP=3,BP=6,
∴=,
解得PE=. (4分)
②EF的长是一个确定的值. (5分)
由①知,==,
∴PE=BE.
同理可得PF=FD. (6分)
∴EF=PE+PF
=BE+FD
=(BE+FD)
=(12+EF),
解得EF=. (7分)
∴EF的长是一个确定的值,其值为. (8分)
(2)相同.
理由:∵AB∥HP,
∴△HPE∽△ABE,
∴==,
∴PE=BE.
同理可得PF=FD. (10分)
∴EF=PE-PF
=BE-FD
=(BE-FD)
=(12+EF),
解得EF=.
∴EF的长与(1)中相同. (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
