初中数学华师版七上4.2.2由视图到立体图形 学案(含答案)
文档属性
| 名称 | 初中数学华师版七上4.2.2由视图到立体图形 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 459.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览

文档简介
4.2.2 由视图到立体图形 学案
学习目标:
1.能根据三视图描述立体图形.
2.培养动手实践的能力和空间想像的能力.
学习重难点:
【重点】由三视图判断出相应的立体图形.
【难点】由三视图想像或者借助实物确定立体图形的形状.
学习过程:
温故而知新:
上节课我们学习了立体图形的三视图,请你画出下列几何体的三视图.
二、创设情境:
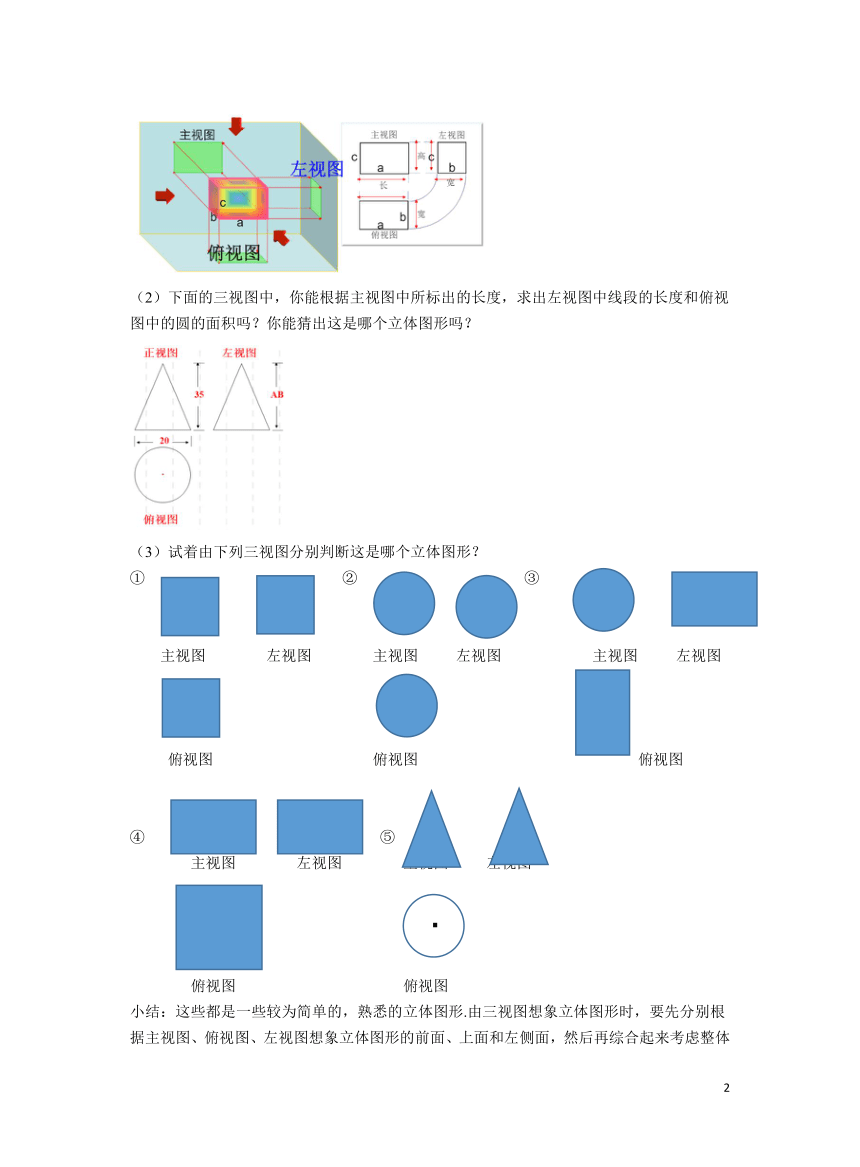
如图是一个螺栓的三视图,工人师傅根据这个三视图就可以制造出这个螺栓了,你知道他是怎么做出来的吗?
主视图 左视图 俯视图
三、新知探究:
1.自主思考,回答问题:
主视图是长方形的是哪个立体图形?
俯视图是圆的是哪个立体图形?
主视图和左视图都是长方形的是哪个立体图形?
主视图、左视图,俯视图都是长方形的是哪个立体图形?
通过上面四个题目,你发现由视图得到立体图形时需要几个视图可以确定立体图形的形状?
小组合作,探究新知:
想一想,我们当时由立体图形得到三视图时,三视图分别反映的是立体图形的哪些量?
(2)下面的三视图中,你能根据主视图中所标出的长度,求出左视图中线段的长度和俯视图中的圆的面积吗?你能猜出这是哪个立体图形吗?
(3)试着由下列三视图分别判断这是哪个立体图形?
① ② ③
主视图 左视图 主视图 左视图 主视图 左视图
俯视图 俯视图 俯视图
④ ⑤
主视图 左视图 主视图 左视图
俯视图 俯视图
小结:这些都是一些较为简单的,熟悉的立体图形.由三视图想象立体图形时,要先分别根据主视图、俯视图、左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
精讲例题:
精讲例1:
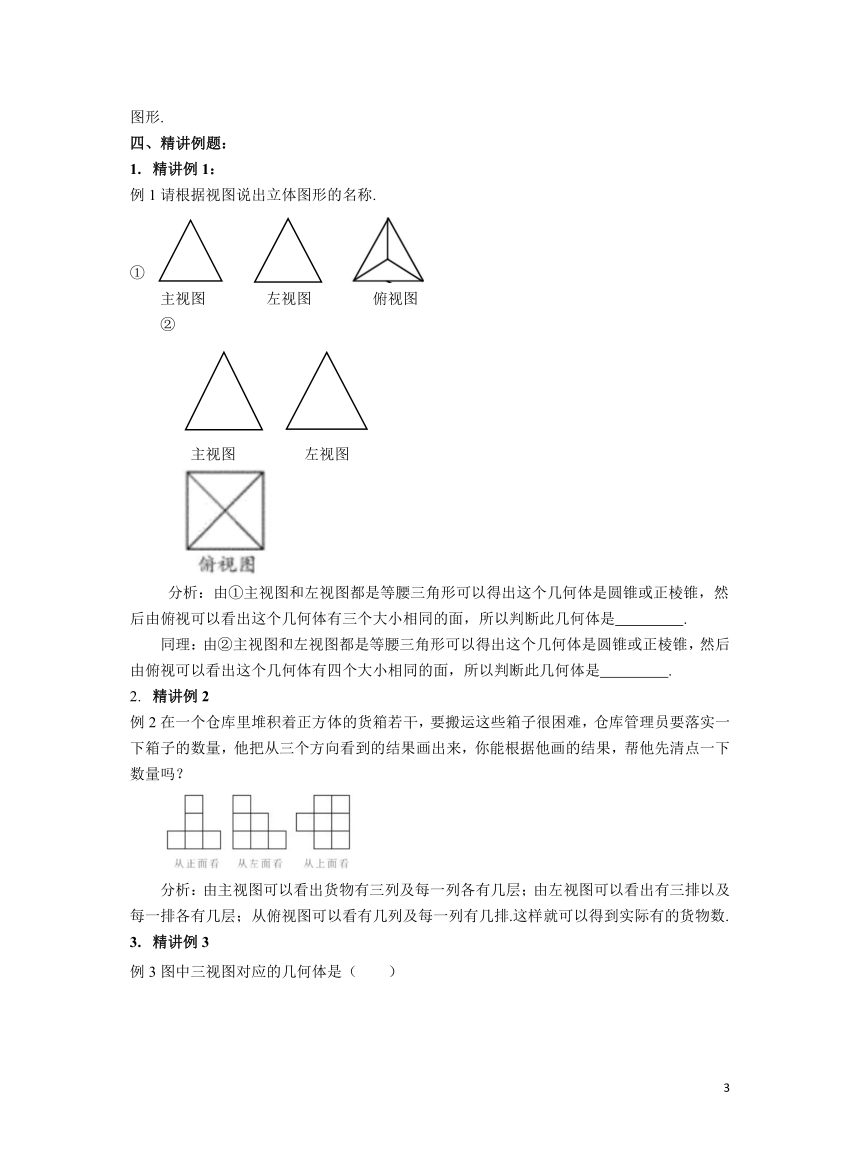
例1请根据视图说出立体图形的名称.
①
主视图 左视图 俯视图
②
主视图 左视图
分析:由①主视图和左视图都是等腰三角形可以得出这个几何体是圆锥或正棱锥,然后由俯视可以看出这个几何体有三个大小相同的面,所以判断此几何体是 .
同理:由②主视图和左视图都是等腰三角形可以得出这个几何体是圆锥或正棱锥,然后由俯视可以看出这个几何体有四个大小相同的面,所以判断此几何体是 .
精讲例2
例2在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,仓库管理员要落实一下箱子的数量,他把从三个方向看到的结果画出来,你能根据他画的结果,帮他先清点一下数量吗?
分析:由主视图可以看出货物有三列及每一列各有几层;由左视图可以看出有三排以及每一排各有几层;从俯视图可以看有几列及每一列有几排.这样就可以得到实际有的货物数.
精讲例3
例3图中三视图对应的几何体是( )
A. B.
C. D.
分析:由主视图和左视图可得此几何体为柱体,根据俯视图可判断出此上面是圆柱体,由此观察图形即可得出结论.
学生试求.
温馨提示:由主视图和左视图可得几何体是柱体,锥体还是球体,由俯视图可确定几何体的具体形状.
小组讨论,总结归纳:
我们由视图到立体图形的,可以先看俯视图,再看主视图,最后看左视图.
堆,码组合图形由视图到立体图形时,俯视图确定列和排;主视图确定列和层;左视图确定排和层。
为了验证“由视图到立体图表”的正确性,可以画出得到立体图形的视图,相同为正确,不同就是出错了.
课堂练习:
1..某几何体的三视图如图所示,该几何体是( )
A.圆柱 B.正方体 C.圆锥 D.三棱柱
2.如图所示三视图的几何体是( )
A. B. C. D.
3.用3个大小相同的小正方体搭成的几何体,从三个方向看到的形状图如图所示,则这个几何体可能是( )
A. B. C. D.
4.如图是从三个方向看到的由一些相同的小正方体构成的几何体的形状图,则构成这个几何体的小正方体的个数是( )
A.8 B.7 C.6 D.5
5.几何体的三视图如图所示,这个几何体是( )
A. B.
C. D.
6.某个几何体的三视图如图所示,该几何体是( )
A. B.
C. D.
7.如图是一个几何体的三视图,则该几何体可能是( )
A. B. C. D.
8.一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,若该几何体所用小立方块的个数为n,则n的最大值为( )
A.10 B.11 C.12 D.13
课堂总结:
本节课你有什么收获?还有哪些疑惑?
布置作业:
课本P
参考答案:
新知探究:
1.自主思考,回答问题:
(1)主视图是长方形的是四棱柱,圆柱等.
(2)俯视图是圆的是圆柱,圆锥,球等.
(3)主视图和左视图都是长方形的是圆柱或四棱柱等.
(4)主视图、左视图,俯视图都是长方形的是长方体(四棱柱)
(5)由视图得到立体图形时需要3个视图可以确定立体图形的形状.
小组合作,探究新知:
(1)由立体图形得到三视图时,主视图分别反映的是立体图形的长和高,左视图反映的是立体图形的宽和高,俯视图反映的是立体图形的长和宽.
(2)左视图中线段AB的长度为35,俯视图中的圆的面积为100,这个几何体是圆锥.
(3)试着由下列三视图分别判断这是哪个立体图形?
①正方体②球③圆柱④长方体⑤圆锥
四、精讲例题:
例1解:正三棱锥.
例2解:由俯视图可得最底层有7个,由正视图和左视力可得第二层有2个,第三层有1个,共有7+2+1=10个,所以实际有10个货箱.
例3解:由主视图可以推出这个几何体是上下两个大小不同柱体,
从主视图推出这两个柱体的宽度不相同,
从俯视图推出上面是圆柱体,直径小于下面柱体的宽.
由此可以判断对应的几何体是选项B.
故选:B.
四、课堂练习:ADBABABD
1
学习目标:
1.能根据三视图描述立体图形.
2.培养动手实践的能力和空间想像的能力.
学习重难点:
【重点】由三视图判断出相应的立体图形.
【难点】由三视图想像或者借助实物确定立体图形的形状.
学习过程:
温故而知新:
上节课我们学习了立体图形的三视图,请你画出下列几何体的三视图.
二、创设情境:
如图是一个螺栓的三视图,工人师傅根据这个三视图就可以制造出这个螺栓了,你知道他是怎么做出来的吗?
主视图 左视图 俯视图
三、新知探究:
1.自主思考,回答问题:
主视图是长方形的是哪个立体图形?
俯视图是圆的是哪个立体图形?
主视图和左视图都是长方形的是哪个立体图形?
主视图、左视图,俯视图都是长方形的是哪个立体图形?
通过上面四个题目,你发现由视图得到立体图形时需要几个视图可以确定立体图形的形状?
小组合作,探究新知:
想一想,我们当时由立体图形得到三视图时,三视图分别反映的是立体图形的哪些量?
(2)下面的三视图中,你能根据主视图中所标出的长度,求出左视图中线段的长度和俯视图中的圆的面积吗?你能猜出这是哪个立体图形吗?
(3)试着由下列三视图分别判断这是哪个立体图形?
① ② ③
主视图 左视图 主视图 左视图 主视图 左视图
俯视图 俯视图 俯视图
④ ⑤
主视图 左视图 主视图 左视图
俯视图 俯视图
小结:这些都是一些较为简单的,熟悉的立体图形.由三视图想象立体图形时,要先分别根据主视图、俯视图、左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
精讲例题:
精讲例1:
例1请根据视图说出立体图形的名称.
①
主视图 左视图 俯视图
②
主视图 左视图
分析:由①主视图和左视图都是等腰三角形可以得出这个几何体是圆锥或正棱锥,然后由俯视可以看出这个几何体有三个大小相同的面,所以判断此几何体是 .
同理:由②主视图和左视图都是等腰三角形可以得出这个几何体是圆锥或正棱锥,然后由俯视可以看出这个几何体有四个大小相同的面,所以判断此几何体是 .
精讲例2
例2在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,仓库管理员要落实一下箱子的数量,他把从三个方向看到的结果画出来,你能根据他画的结果,帮他先清点一下数量吗?
分析:由主视图可以看出货物有三列及每一列各有几层;由左视图可以看出有三排以及每一排各有几层;从俯视图可以看有几列及每一列有几排.这样就可以得到实际有的货物数.
精讲例3
例3图中三视图对应的几何体是( )
A. B.
C. D.
分析:由主视图和左视图可得此几何体为柱体,根据俯视图可判断出此上面是圆柱体,由此观察图形即可得出结论.
学生试求.
温馨提示:由主视图和左视图可得几何体是柱体,锥体还是球体,由俯视图可确定几何体的具体形状.
小组讨论,总结归纳:
我们由视图到立体图形的,可以先看俯视图,再看主视图,最后看左视图.
堆,码组合图形由视图到立体图形时,俯视图确定列和排;主视图确定列和层;左视图确定排和层。
为了验证“由视图到立体图表”的正确性,可以画出得到立体图形的视图,相同为正确,不同就是出错了.
课堂练习:
1..某几何体的三视图如图所示,该几何体是( )
A.圆柱 B.正方体 C.圆锥 D.三棱柱
2.如图所示三视图的几何体是( )
A. B. C. D.
3.用3个大小相同的小正方体搭成的几何体,从三个方向看到的形状图如图所示,则这个几何体可能是( )
A. B. C. D.
4.如图是从三个方向看到的由一些相同的小正方体构成的几何体的形状图,则构成这个几何体的小正方体的个数是( )
A.8 B.7 C.6 D.5
5.几何体的三视图如图所示,这个几何体是( )
A. B.
C. D.
6.某个几何体的三视图如图所示,该几何体是( )
A. B.
C. D.
7.如图是一个几何体的三视图,则该几何体可能是( )
A. B. C. D.
8.一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,若该几何体所用小立方块的个数为n,则n的最大值为( )
A.10 B.11 C.12 D.13
课堂总结:
本节课你有什么收获?还有哪些疑惑?
布置作业:
课本P
参考答案:
新知探究:
1.自主思考,回答问题:
(1)主视图是长方形的是四棱柱,圆柱等.
(2)俯视图是圆的是圆柱,圆锥,球等.
(3)主视图和左视图都是长方形的是圆柱或四棱柱等.
(4)主视图、左视图,俯视图都是长方形的是长方体(四棱柱)
(5)由视图得到立体图形时需要3个视图可以确定立体图形的形状.
小组合作,探究新知:
(1)由立体图形得到三视图时,主视图分别反映的是立体图形的长和高,左视图反映的是立体图形的宽和高,俯视图反映的是立体图形的长和宽.
(2)左视图中线段AB的长度为35,俯视图中的圆的面积为100,这个几何体是圆锥.
(3)试着由下列三视图分别判断这是哪个立体图形?
①正方体②球③圆柱④长方体⑤圆锥
四、精讲例题:
例1解:正三棱锥.
例2解:由俯视图可得最底层有7个,由正视图和左视力可得第二层有2个,第三层有1个,共有7+2+1=10个,所以实际有10个货箱.
例3解:由主视图可以推出这个几何体是上下两个大小不同柱体,
从主视图推出这两个柱体的宽度不相同,
从俯视图推出上面是圆柱体,直径小于下面柱体的宽.
由此可以判断对应的几何体是选项B.
故选:B.
四、课堂练习:ADBABABD
1
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
