江西省上饶县中学2014-2015学年高一上学期第三次月考数学试题
文档属性
| 名称 | 江西省上饶县中学2014-2015学年高一上学期第三次月考数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 229.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-27 00:00:00 | ||
图片预览


文档简介
时间:120分钟 总分:150分
一、选择题
1、函数的定义域为
A. (0,3) B. C. D.
2、已知集合,,则使成立的实数的取值范围是
A. B. C. D. φ
3、设函数,则的值为
A. B. C. D. 18
4、一个球的表面积是16,那么这个球的体积为
A. B. C. 16 D. 24
5、△ABC的斜二侧直观图如图所示,则△ABC的在面积为
A. 1 B. 2
C. D.
6、在△ABC中,AB=3,BC=4,ABC=120,若把△ABC
绕直线AB旋转一周,则所形成的几何体体积是
A. 11π B. 12π
C. 13π D. 14π
7、已知函数,,则的值是
A. 19 B. 13 C. -19 D. -13
8、下列式子中成立的是
A. B. C. D.
9、已知m,n表示两条不同直线,表示平面,下列说法正确的是
A. 若,,则 B. 若,则
C. 若,,则 D. 若,,则
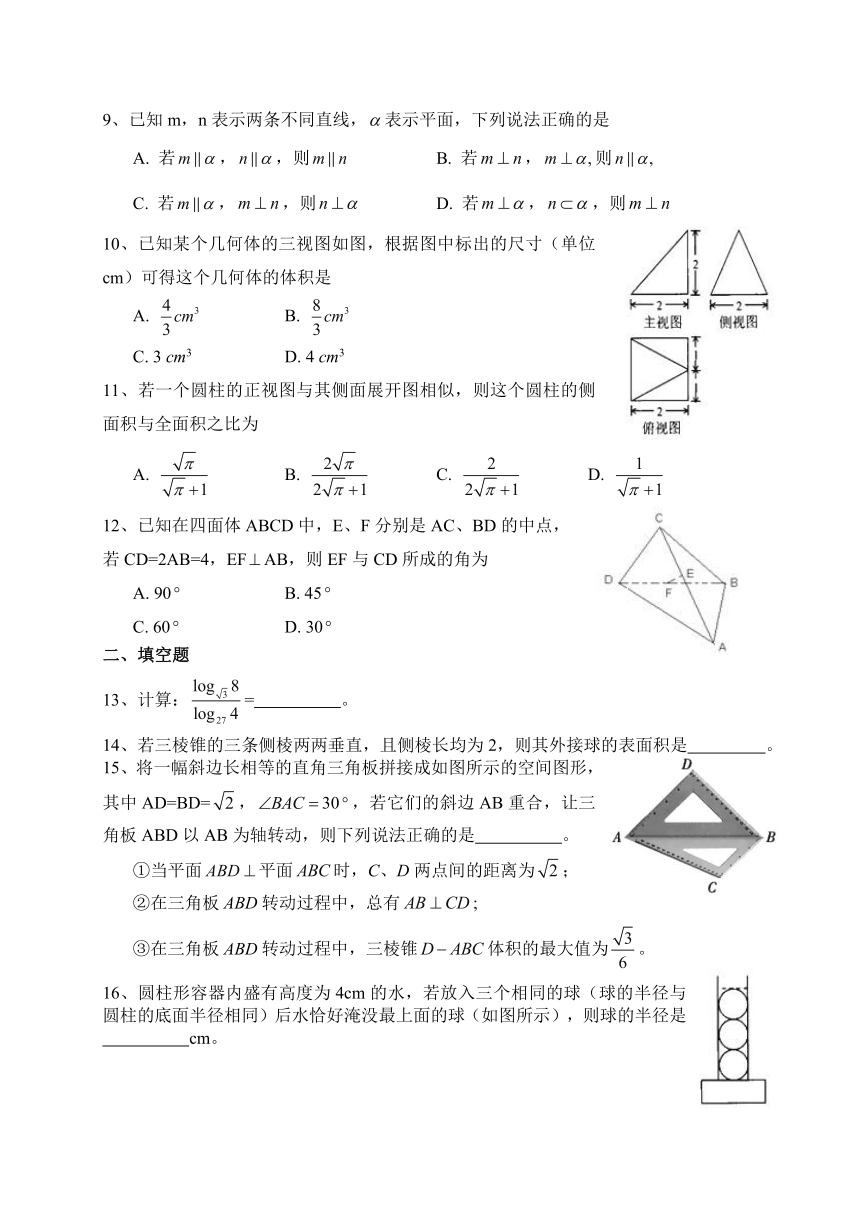
10、已知某个几何体的三视图如图,根据图中标出的尺寸(单位cm)可得这个几何体的体积是
A. B.
C. 3 cm3 D. 4 cm3
11、若一个圆柱的正视图与其侧面展开图相似,则这个圆柱的侧面积与全面积之比为
A. B. C. D.
12、已知在四面体ABCD中,E、F分别是AC、BD的中点,
若CD=2AB=4,EFAB,则EF与CD所成的角为
A. 90 B. 45
C. 60 D. 30
二、填空题
13、计算:= 。
14、若三棱锥的三条侧棱两两垂直,且侧棱长均为2,则其外接球的表面积是 。
15、将一幅斜边长相等的直角三角板拼接成如图所示的空间图形,其中AD=BD=,30,若它们的斜边AB重合,让三角板ABD以AB为轴转动,则下列说法正确的是 。
①当平面平面时,C、D两点间的距离为;
②在三角板ABD转动过程中,总有;
③在三角板ABD转动过程中,三棱锥体积的最大值为。
16、圆柱形容器内盛有高度为4cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后水恰好淹没最上面的球(如图所示),则球的半径是
cm。
三、解答题
17、已知是偶函数,当时,。
(1)求的解析式;
(2)若不等式在时都成立,求m的取值范围。
18、如图,在正方体中,
(1)求证:直线面;
(2)若,求四棱锥的体积。
19、如图,在棱长为2的正方体中,E为棱CC1的中点。
(1)求证:;
(2)求点A到平面BDE的距离。
20、设函数,
(1)若,求t取值范围;
(2)求的最值,并给出最值时对应的x的值。
21、三棱柱中,侧棱与底面垂直,,,M,N分别是A1B1,AC1的中点。
(1)求证:;
(2)求证:平面
22、已知多面体ABCDFE中,四边形ABCD为矩形,,,平面平面ABCD,O、M分别为AB、FC的中点,且AB=2,AD=EF=1。
(1)求证:AF⊥平面FBC;
(2)求证:OM∥平面DAF;
(3)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD∶VF-CBE 的值.
上饶县中学高一第三次月考数学试卷答案
18.解:(1)BB1⊥平面A1B1C1D1,且A1C1?平面A1B1C1D1, ∴BB1⊥A1C1…(2分)
∵四边形A1B1C1D1为正方形, ∴B1D1⊥A1C1
又∵BB1?平面BDD1B1,B1D1?平面BDD1B1,BB1∩B1D1=B ∴直线A1C1⊥面BDD1B1;
(2)∵AA1=2,可得正方形ABCD的边长等于2, ∴正方形ABCD的面积S=2×2=4
∵DD1⊥平面ABCD,∴DD1为四棱锥D1-ABCD的高∴V?D1?ABCD=×SABCD×DD1=, 即四棱锥四棱锥D1-ABCD的体积为.
19.(1)连结AC
∵ABCD-A1B1C1D1是正方体,∴
又∵, ∴
又∵, ∴
又∵,∴
(2)设A到面BDE的距离为h
∵正方体的棱长为2,E为CC中点,
∴BE=DE=,,∴
∴ ∴
20. :(1)
即
当
21.解:(1)取BC1的中点D,连接B1D、ND
∵D、N分别是BC1、AC1的中点
∴
∴MNDB1为平行四边形
∴,且B1D面BCC1B1
∴
(2)由题可知
且
∴
又
∴MN
∴面
22. 解:(Ⅰ)平面ABEF⊥平面ABCD ,平面ABEF平面ABCD=AB
BC平面ABCD,而四边形ABCD为矩形 BC⊥AB ,
BC⊥平面ABEF
AF平面ABEF BCAF BFAF,BCBF=B
AF⊥平面FBC
(Ⅱ)取FD中点N,连接MN、AN,则MN∥CD,且 MN=CD,又四边形ABCD为矩形,
MN∥OA,且MN=OA 四边形AOMN为平行四边形,OM∥ON
又OM平面DAF,ON平面DAF OM∥平面DAF
(Ⅲ)过F作FGAB与G ,由题意可得:FG平面ABCD
VF-ABCD =S矩形ABCDE·FG = FG
CF平面ABEF VF-CBE = VC-BFE =S△BFE·CB = = FG
VF-ABCD∶VF-CBE = 4∶1
同课章节目录
