吉林省长春市第四十五中学2023-2024学年九年级上学期9月月考数学试题(无答案)
文档属性
| 名称 | 吉林省长春市第四十五中学2023-2024学年九年级上学期9月月考数学试题(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 385.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览

文档简介
九年级数学阶段练习B
一、选择题(每小题3分,共24分)
1.下列各数中比小的是
(A). (B). (C). (D).
2.最新发售的华为Mate X5的芯片是麒麟9000S,这是一款5G芯片,采用7纳米工艺制程.已知1纳米米,用科学记数法将7纳米表示为
(A)米. (B)米. (C)米. (D)米
3.将“厉害了我的国”这六个字分别写在一个正方体的六个面上.若这个正方体的展开图如图所示,则在这个正方体中,与“厉”字相对的字是
(A)“了” (B)“我” (C)“的” (D)“国”
4.某校“校园好声音”比赛中,某组参赛选手得分如下(单位:分):) 9,7,8,7,9,7,6.则该组参赛选手得分的中位数是
(A)9分. (B)8分 (C)7分 (D)6分
5.下列整数中与的结果最接近的是
(A)3. (B)4. (C)9. (D)18.
6.如图,在地面上的A点处测得树顶B的仰角为α度,若米,则树高为
(A)米 (B)米. (C)米 (D)米.
7.如图,,正五边形的顶点A、B分别落在、上,若,则的大小为
(A) (B) (C) (D)
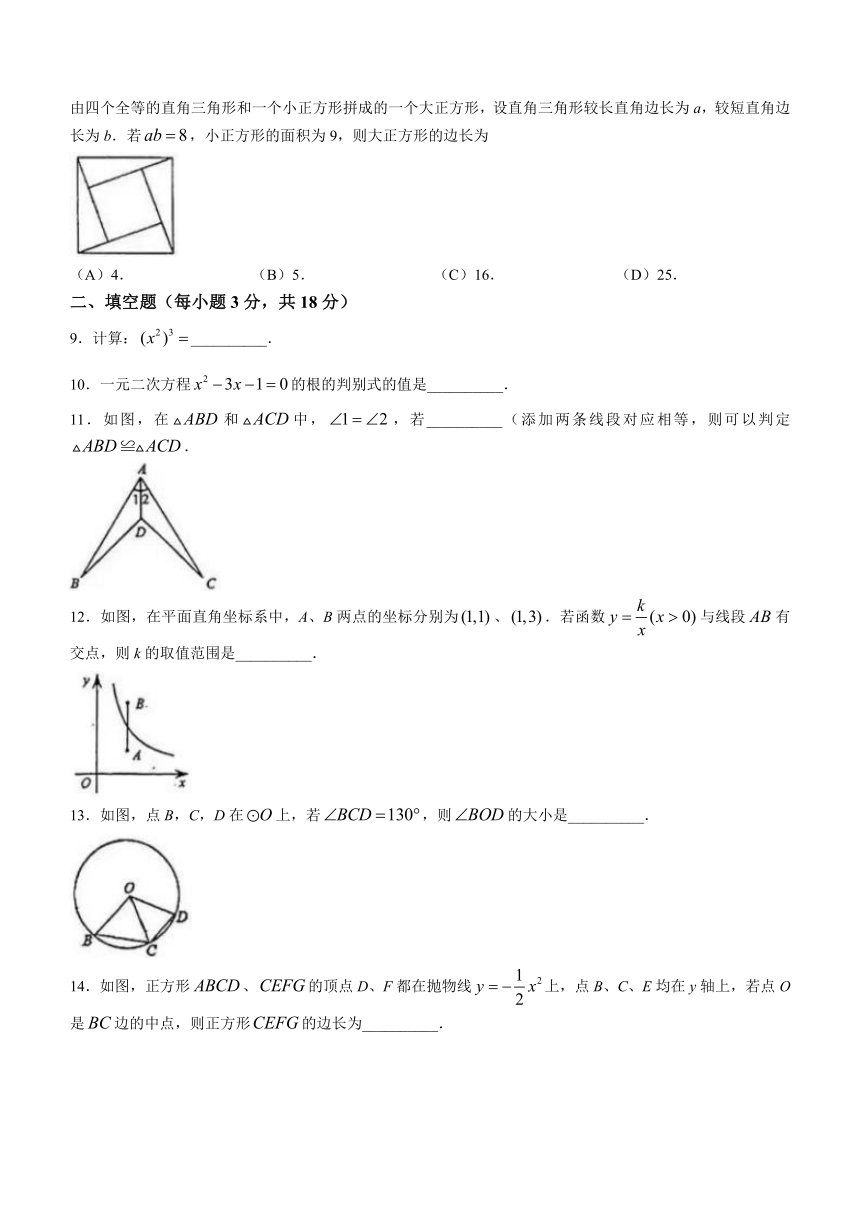
8.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“:赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b.若,小正方形的面积为9,则大正方形的边长为
(A)4. (B)5. (C)16. (D)25.
二、填空题(每小题3分,共18分)
9.计算:__________.
10.一元二次方程的根的判别式的值是__________.
11.如图,在和中,,若__________(添加两条线段对应相等,则可以判定.
12.如图,在平面直角坐标系中,A、B两点的坐标分别为、.若函数与线段有交点,则k的取值范围是__________.
13.如图,点B,C,D在上,若,则的大小是__________.
14.如图,正方形、的顶点D、F都在抛物线上,点B、C、E均在y轴上,若点O是边的中点,则正方形的边长为__________.
三、解答题(本大题10小题,共78分)
15.(6分)先化简,再求值:,其中,.
16.(6分)在一个不透明的布袋中只装有2个白色围棋子和1个黑色围棋子,围棋子除颜色外其余均相同.从这个布袋中随机地摸出1个围棋子,记下颜色后放回,搅匀后再随机地摸出1个围棋子记下颜色,请用画树状图(或列表)的方法,求两次摸出的围棋子颜色都是白色的概率.
17.(6分)小明准备抄写600个汉字练习书法,原计划每天抄写相同数量的汉字.在抄写100个汉字后,为了提前完成任务,每天的练字数量是原来的2倍,结果共用7天完成了任务.求小明原来每天抄写汉字的个数.
18.(7分)图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,线段、的端点均在格点上,在图①、图②、图③给定的网格中以、为边各画一个四边形,使第四个顶点在格点上,要求:
(1)所画的三个四边形均有一组邻边相等.
(2)所画的三个四边形不全等.
19.(7分)在学校组织的“反电诈”安全教育竞赛中,每班参加比赛的人数相同,成绩分为A、B、C、D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.学校将九年级一班和二班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩为D级的人数为_________人;
(2)请你将表格补充完整:
平均数(分) 中位数(分) 众数(分)
一班 87.6 90
二班 87.6 100
(3)若该校九年级共有学生800人,试估计九年级学生成绩等级为A级的人数.
20.(7分)如图,直线经过上的点A,且,.求证:直线是的切线.
21.(8分)如图①,水平放置的空圆柱形容器内放着一个实心的铁“柱锥体”(由一个高为的圆柱和一个同底面的高为圆锥组成的铁几何体)向这个容器内匀速注水,水流速度为,注满为止.整个注水过程中,水面高度与注水时间之间的函数关系如图②所示.
(1)圆柱形容器的高为_________.
(2)求线段所对应的函数表达式.
(3)直接写出“锥体”顶端距离水面时的值.
22.(9分)如图,在矩形中,,.点P从点C出发,沿折线以每秒1个单位长度的速度运动至点A.连接,设点P运动的时间为x(秒).
(1)当点P在线段上时,用含x的式子表示P、A两点间的距离.
(2)当点P不与A、C重合时,设线段与线段所夹锐角的正切值为y,求y与x之间的函数关系式.
(3)直接写出线段的垂直平分线经过矩形的顶点时x的值.
23.(10分)如图,在边长为9的正方形中,动点E、F分别在边、上,将正方形沿直线折叠,使点B的对应点始终落在边上(点不与点A、D重合),点C落在点处,与交于点P,连接,作点H.
(1)感知:①当时,的大小为________.
②求的长.
(2)探究:当在边上位置变化时,的周长是否发生变化?如变化,请说明理由;如不变,请求出该定值.
(3)应用:若,直接写出五边形的周长.
24.(12分)已知函数(n为常数)
(1)当时,
①求此函数与y轴交点坐标.
②若点在此函数图象上,求b的值.
(2)当此函数图象的最高点到x轴的距离为1时,求n的值.
(3)已知、,当此函数的图象与线段只有一个交点时,直接写出n的取值范围.
一、选择题(每小题3分,共24分)
1.下列各数中比小的是
(A). (B). (C). (D).
2.最新发售的华为Mate X5的芯片是麒麟9000S,这是一款5G芯片,采用7纳米工艺制程.已知1纳米米,用科学记数法将7纳米表示为
(A)米. (B)米. (C)米. (D)米
3.将“厉害了我的国”这六个字分别写在一个正方体的六个面上.若这个正方体的展开图如图所示,则在这个正方体中,与“厉”字相对的字是
(A)“了” (B)“我” (C)“的” (D)“国”
4.某校“校园好声音”比赛中,某组参赛选手得分如下(单位:分):) 9,7,8,7,9,7,6.则该组参赛选手得分的中位数是
(A)9分. (B)8分 (C)7分 (D)6分
5.下列整数中与的结果最接近的是
(A)3. (B)4. (C)9. (D)18.
6.如图,在地面上的A点处测得树顶B的仰角为α度,若米,则树高为
(A)米 (B)米. (C)米 (D)米.
7.如图,,正五边形的顶点A、B分别落在、上,若,则的大小为
(A) (B) (C) (D)
8.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“:赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b.若,小正方形的面积为9,则大正方形的边长为
(A)4. (B)5. (C)16. (D)25.
二、填空题(每小题3分,共18分)
9.计算:__________.
10.一元二次方程的根的判别式的值是__________.
11.如图,在和中,,若__________(添加两条线段对应相等,则可以判定.
12.如图,在平面直角坐标系中,A、B两点的坐标分别为、.若函数与线段有交点,则k的取值范围是__________.
13.如图,点B,C,D在上,若,则的大小是__________.
14.如图,正方形、的顶点D、F都在抛物线上,点B、C、E均在y轴上,若点O是边的中点,则正方形的边长为__________.
三、解答题(本大题10小题,共78分)
15.(6分)先化简,再求值:,其中,.
16.(6分)在一个不透明的布袋中只装有2个白色围棋子和1个黑色围棋子,围棋子除颜色外其余均相同.从这个布袋中随机地摸出1个围棋子,记下颜色后放回,搅匀后再随机地摸出1个围棋子记下颜色,请用画树状图(或列表)的方法,求两次摸出的围棋子颜色都是白色的概率.
17.(6分)小明准备抄写600个汉字练习书法,原计划每天抄写相同数量的汉字.在抄写100个汉字后,为了提前完成任务,每天的练字数量是原来的2倍,结果共用7天完成了任务.求小明原来每天抄写汉字的个数.
18.(7分)图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,线段、的端点均在格点上,在图①、图②、图③给定的网格中以、为边各画一个四边形,使第四个顶点在格点上,要求:
(1)所画的三个四边形均有一组邻边相等.
(2)所画的三个四边形不全等.
19.(7分)在学校组织的“反电诈”安全教育竞赛中,每班参加比赛的人数相同,成绩分为A、B、C、D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.学校将九年级一班和二班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩为D级的人数为_________人;
(2)请你将表格补充完整:
平均数(分) 中位数(分) 众数(分)
一班 87.6 90
二班 87.6 100
(3)若该校九年级共有学生800人,试估计九年级学生成绩等级为A级的人数.
20.(7分)如图,直线经过上的点A,且,.求证:直线是的切线.
21.(8分)如图①,水平放置的空圆柱形容器内放着一个实心的铁“柱锥体”(由一个高为的圆柱和一个同底面的高为圆锥组成的铁几何体)向这个容器内匀速注水,水流速度为,注满为止.整个注水过程中,水面高度与注水时间之间的函数关系如图②所示.
(1)圆柱形容器的高为_________.
(2)求线段所对应的函数表达式.
(3)直接写出“锥体”顶端距离水面时的值.
22.(9分)如图,在矩形中,,.点P从点C出发,沿折线以每秒1个单位长度的速度运动至点A.连接,设点P运动的时间为x(秒).
(1)当点P在线段上时,用含x的式子表示P、A两点间的距离.
(2)当点P不与A、C重合时,设线段与线段所夹锐角的正切值为y,求y与x之间的函数关系式.
(3)直接写出线段的垂直平分线经过矩形的顶点时x的值.
23.(10分)如图,在边长为9的正方形中,动点E、F分别在边、上,将正方形沿直线折叠,使点B的对应点始终落在边上(点不与点A、D重合),点C落在点处,与交于点P,连接,作点H.
(1)感知:①当时,的大小为________.
②求的长.
(2)探究:当在边上位置变化时,的周长是否发生变化?如变化,请说明理由;如不变,请求出该定值.
(3)应用:若,直接写出五边形的周长.
24.(12分)已知函数(n为常数)
(1)当时,
①求此函数与y轴交点坐标.
②若点在此函数图象上,求b的值.
(2)当此函数图象的最高点到x轴的距离为1时,求n的值.
(3)已知、,当此函数的图象与线段只有一个交点时,直接写出n的取值范围.
同课章节目录
