浙江省高考数学自主命题特点分析与后期复习安排
文档属性
| 名称 | 浙江省高考数学自主命题特点分析与后期复习安排 |

|
|
| 格式 | rar | ||
| 文件大小 | 304.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-12 00:00:00 | ||
图片预览









文档简介
课件50张PPT。浙江省高考数学自主命题特点分析
与后期复习安排杭州市学军中学 冯定应
Fengdy@hzxjhs.com一.命题者如是说:(1)稳定不固定
(2)前进不急进
(3)简约不简单从内容上看:
十分关注大纲和考试说明,不超、不偏、不怪;
不追求覆盖率;背景公平、叙述简洁、清楚,没有
歧义。重视通性、通法,不追求特殊技巧。
从数学本质上看:
十分关注对数学概念和问题本质的理解,重视理性思维;
理科重在思维的深刻性、逻辑性和分析问题的能力;
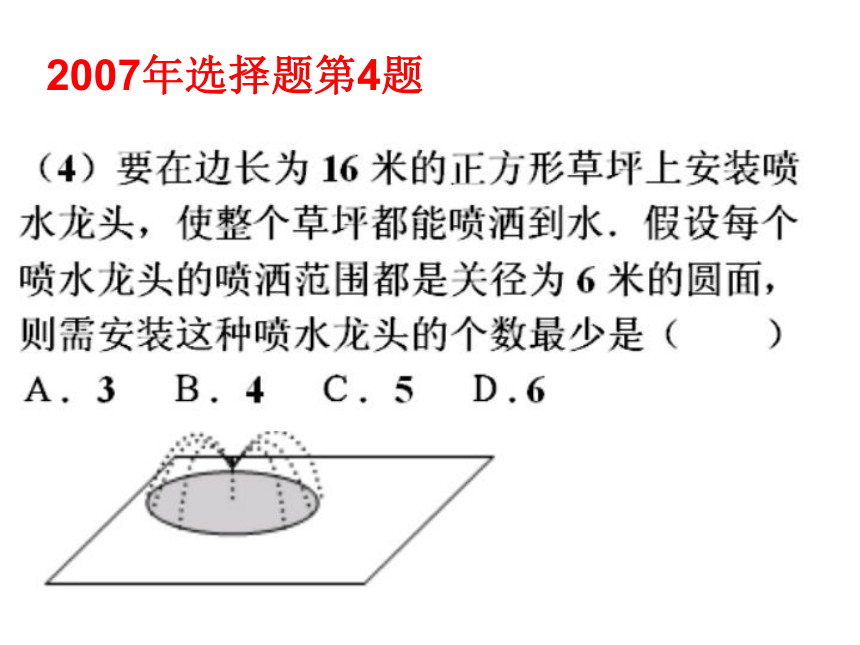
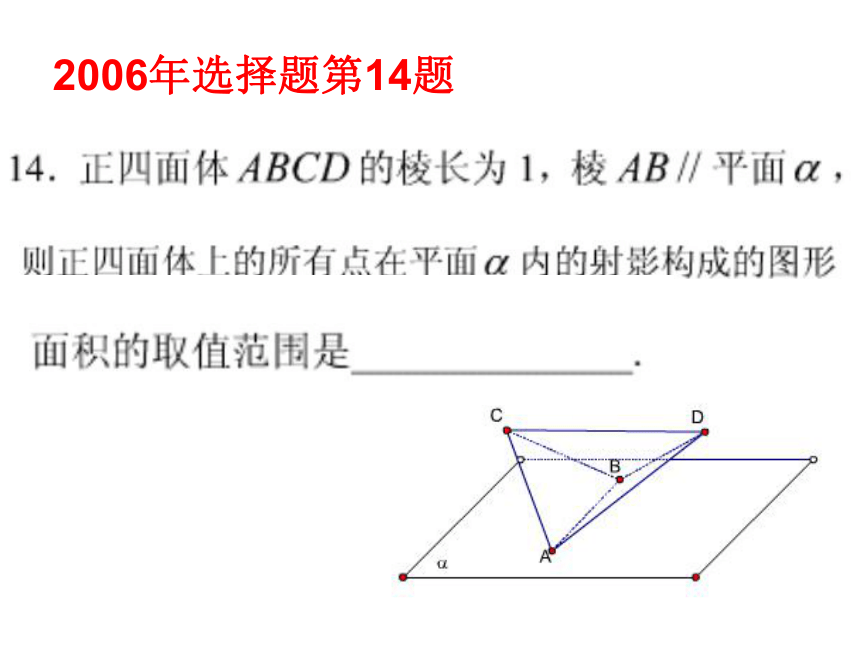
文科重在知识的应用性、基础性和数学运算、表达能力。二、具有浙江高考命题特色的考题分析1.概念的深刻性2004年选择题第11题2006年选择题第10题2007年选择题第10题二、具有浙江高考命题特色的考题分析2.思维的灵活性2006年选择题第8题2007年选择题第4题2006年选择题第14题浙江省考试说明中的最后一道题:
已知数列{xn},(n为正整数)
满足xnn +xn –1=0, xn >0,证明:
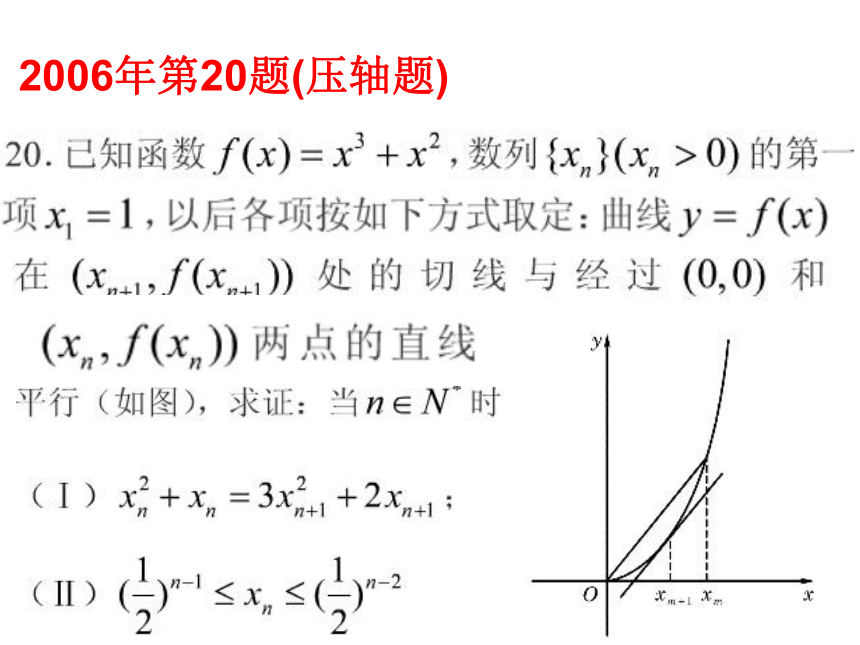
2006年第20题(压轴题)4.立体几何
立体几何的考查是“一大两小”.
除了“一小”是线面位置关系外,
其余主要是:
(1)线线角?
(2)线面角?
(3)面面角?
(4)点到面的距离
(5)平行与垂直立体几何大题作为高考试验田的地位有所下降??? 18.如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= , AF=1,
M是线段EF的中点。 (1)求证AM//平面BDE; (2)求二面角A?DF?B; (3)试在线段AC上确定一点P,使得PF与BC所成的角是60?。
04年高考:
一题两法考察全面04年第18题05年:难度加大,题序后置,思想方法一致5.解析几何:一大三小或一大二小
?解几的考查重点是直线与圆锥曲线的关系,
设问灵活,立意较高.
两大重点内容是:轨迹(注意定义法求轨迹)与最值.
运算量正在增大,参数讨论问题蓄势待发.
参数范围题以及融综合性,开放性,探索性为一体的能力题.设立为压轴题的可能性进一步下降21.已知双曲线的中心在原点,右顶点为A(1,0),点P、Q在双曲线的右支上,点M(m,0)到直线AP的距离为1, (1)若直线AP的斜率为k,且|k|?[ ], 求实数m的取值范围; (2)当m= +1时,△APQ的内心恰好是点M,求此双曲线的方程。 04年高考:倒数第二题
平实、通法,要有比较强的运算能力 (Ⅱ)若直线上 的动点,使 最大的点P记为Q,求点Q的坐标(用m表示).?
17.如图,已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,长轴A1A2的长为4,左准线 轴的交点为M,|MA1|∶|A1F1|=2∶1.
(Ⅰ)求椭圆的方程;
05年高考:倒数第四题
思想方法全面,
难度与去年基本相同二、具有浙江高考命题特色的考题分析6.三角函数突出”函数与变换”的双重特性.
7.线性规划、分布列、正态分布、统计重视知识点
的落实.
8.应用题:有好的应用题不拒绝,没有恰当的应用题
也不强求.
9.函数、导数、不等式、数列的综合问题作为压轴
题的可能性仍然比较大。
10.主干内容保持了较高的比例复习中既全面有要
突出重点。重点问题重点考、热点问题不回避、
设置难点考能力.
三、第二轮复习的基本思路(一)、 分析高考试题,明确考试热点;
(二)、学习考试说明,调整复习策略;
(三)、剖析重点章节,重视联系转化;
(四)、研究通性通法,提高复习实效;
(一)、 分析高考试题,明确考试热点;
三条建议
(1)老师逐个题目作一遍.
(2)同一备课组的老师再进行演讨.
(3)把自己出的模拟题逐个与高考题比较. 确定复习策略的依据有两条:
一是高考的考试大纲(或《考试说明》),
二是自己的学生的实际情况。
因为复习工作的目的:
就是努力使自己的数学水平达到考试大纲的要求。
经常梳理自己的知识系统,结合自己学生的具体
情况制定数学复习策略,及时调整数学复习方法,
是每一位老师都需要重视的工作。
只有摸清自己学生的易忘、易错、易混点,
才能有的放矢地完善学科知识和能力结构,
明确复习重点。 (二)、学习考试说明,调整复习策略;第一轮复习:
老师是矛盾的主要方面,
高考的内容,要求是复习的主要依据第二轮复习:
学生是矛盾的主要方面,
学生尽可能努力适应高考的要求,
是复习工作的主要依据.第二轮复习:
真正让学生成为复习的主体,主动查漏补缺 :
老师应该:种好自己责任田,不占学生自留地指导学生回到课本:在第一轮复习后,
(1)每个章节都勾出一些课本题目,
要求人人过关。
(2)将解决这一些问题的通性通法,
常见的变形思路、方法
以及这部分的知识可能与哪些知识有联系.
印成讲义发给学生,
让学生对这章学习内容再作一次强化。保证人人得好基本分(三)、剖析重点章节,重视联系转化;综合运用能力的四个核心内容:
函数、数列、不等式和解析几何<1> “基本不等式”
<2>“平面向量的数量积”
<3>“同角三角函数的基本关系式”
<4>“两角和与差的正弦、余弦、正切”综合运用能力还涉及到的11个知识点<5>“等差数列” ;<6>“等比数列”
<7>“椭圆的标准方程和几何性质
<8>“双曲线的标准方程和几何性质
<9>“抛物线的标准方程和几何性质
<10>“函数的基本性质”
<11>“直线和平面垂直的判定和性质”1、强化练习讲评
第一、题组式讲评
练习中经常出现相似错误的题型或概念性题型,
常采用题组方式进行讲评,矫正出现的错误.
第二、发散式讲评
对于一些重要题型,常采用一题多解、一题多变
的方式进行讲评,培养求异思维,促进能力形成,
强化重点题型、重要方法的理解与领悟,起到触类
旁通的作用.
第三、收敛式讲评
对一些解法相同或相近题型常采用多题一解的收敛
方式进行讲评,讲评侧重对通性通法进行归纳,真
正起到“一把钥匙能开千把锁”的作用.(四)、研究通性通法,提高复习实效;2.从高考阅卷情况,看提高教学的实效
阅卷中发现考生存在的一些问题:
<1>“概念不清”;
<2>“推理过程混乱、不规范”;
<3>“计算能力较差”;
<4>“平面几何知识薄弱”等。做好回归课本与反思注重解题规范训练注重独立解题训练注重平面几何小、活、巧的结论应用3.注意四种数学思想方法的运用(1).函数方程思想
(2).分类讨论思想
(3).数形结合思想
(4).化归转化思想课例一:研究性问题1.y2=4x上有一条长为m的弦,求AB中点
横坐标的最小值.
2.x2=4y上的一部分恰好是高为4cm的酒
杯的横截面.要让半径为r冰球能够直接落
到酒杯的底部,求冰球半径r最大值.课例二:分类讨论问题知识背景 ---没有无缘无故的分类 1.为什么要分类讨论 例1.解不等式. 或或例1.解不等式. 例2.设函数
(Ⅰ)判断函数的奇偶数;
(Ⅱ)求函数的最小值.例3.已知轴截面的顶角为 ,母线长为 ,求经过两条母线的截面面积最大值.问题4解答:设两母线所成的角为把握分类依据---不重不漏 分类讨论问题1.为什么要分类讨论 2.如何进行分类讨论 例4.设函数
(Ⅰ)判断函数的奇偶数;
(Ⅱ)求函数的最小值.归纳要全面,不重也不漏例5.甲、乙两地相距1000公里,汽车运货物从甲地匀速运往乙地,为保证安全, 汽车的最高时速不得超过100公里,若汽车每小时的运输成本(以元为单位)由两部分组成: ⑴ 固定成本为100;
⑵ 可变成本部分与速度平方成正比例,比例系数是b(b>0);
为使全程运输成本最低,求汽车的行驶速度。解:假设行驶速度为v,y=固定成本+可变成本例5解答:有化有归例6. 设点P到M(-1,0)、
N(1,0)两点距离之差为2m,到x轴、y轴距离之比为2,求m的取值范围.分析(略)例7.某城市2001年末汽车保有量
为30万辆,预计此后每年报废上一
年末汽车保有量的6%,并且每年新
增汽车数量相同.为保护城市环境,
要求该城市汽车保有量不超过60万
辆,那么每年新增汽车数量不应超
过多少辆?解:设从2001年起每年的汽车保有量
则:……(1)当 时, 递增,要使
即只需 万辆
即
(2)当 时, 递减,
即 时,成立.
(3)当 时,
综上, 万时,满足要求.有化有归( 小 结 ) (1).知识背景----清 (2).分类依据----明 (3).不重不漏,有化有归 没有无缘无故的分类分类讨论问题3.把握分类的几个基本原则 欢迎老师们批评指正!以上个人主观意见,
难免有许多失之偏颇。再见!
与后期复习安排杭州市学军中学 冯定应
Fengdy@hzxjhs.com一.命题者如是说:(1)稳定不固定
(2)前进不急进
(3)简约不简单从内容上看:
十分关注大纲和考试说明,不超、不偏、不怪;
不追求覆盖率;背景公平、叙述简洁、清楚,没有
歧义。重视通性、通法,不追求特殊技巧。
从数学本质上看:
十分关注对数学概念和问题本质的理解,重视理性思维;
理科重在思维的深刻性、逻辑性和分析问题的能力;
文科重在知识的应用性、基础性和数学运算、表达能力。二、具有浙江高考命题特色的考题分析1.概念的深刻性2004年选择题第11题2006年选择题第10题2007年选择题第10题二、具有浙江高考命题特色的考题分析2.思维的灵活性2006年选择题第8题2007年选择题第4题2006年选择题第14题浙江省考试说明中的最后一道题:
已知数列{xn},(n为正整数)
满足xnn +xn –1=0, xn >0,证明:
2006年第20题(压轴题)4.立体几何
立体几何的考查是“一大两小”.
除了“一小”是线面位置关系外,
其余主要是:
(1)线线角?
(2)线面角?
(3)面面角?
(4)点到面的距离
(5)平行与垂直立体几何大题作为高考试验田的地位有所下降??? 18.如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= , AF=1,
M是线段EF的中点。 (1)求证AM//平面BDE; (2)求二面角A?DF?B; (3)试在线段AC上确定一点P,使得PF与BC所成的角是60?。
04年高考:
一题两法考察全面04年第18题05年:难度加大,题序后置,思想方法一致5.解析几何:一大三小或一大二小
?解几的考查重点是直线与圆锥曲线的关系,
设问灵活,立意较高.
两大重点内容是:轨迹(注意定义法求轨迹)与最值.
运算量正在增大,参数讨论问题蓄势待发.
参数范围题以及融综合性,开放性,探索性为一体的能力题.设立为压轴题的可能性进一步下降21.已知双曲线的中心在原点,右顶点为A(1,0),点P、Q在双曲线的右支上,点M(m,0)到直线AP的距离为1, (1)若直线AP的斜率为k,且|k|?[ ], 求实数m的取值范围; (2)当m= +1时,△APQ的内心恰好是点M,求此双曲线的方程。 04年高考:倒数第二题
平实、通法,要有比较强的运算能力 (Ⅱ)若直线上 的动点,使 最大的点P记为Q,求点Q的坐标(用m表示).?
17.如图,已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,长轴A1A2的长为4,左准线 轴的交点为M,|MA1|∶|A1F1|=2∶1.
(Ⅰ)求椭圆的方程;
05年高考:倒数第四题
思想方法全面,
难度与去年基本相同二、具有浙江高考命题特色的考题分析6.三角函数突出”函数与变换”的双重特性.
7.线性规划、分布列、正态分布、统计重视知识点
的落实.
8.应用题:有好的应用题不拒绝,没有恰当的应用题
也不强求.
9.函数、导数、不等式、数列的综合问题作为压轴
题的可能性仍然比较大。
10.主干内容保持了较高的比例复习中既全面有要
突出重点。重点问题重点考、热点问题不回避、
设置难点考能力.
三、第二轮复习的基本思路(一)、 分析高考试题,明确考试热点;
(二)、学习考试说明,调整复习策略;
(三)、剖析重点章节,重视联系转化;
(四)、研究通性通法,提高复习实效;
(一)、 分析高考试题,明确考试热点;
三条建议
(1)老师逐个题目作一遍.
(2)同一备课组的老师再进行演讨.
(3)把自己出的模拟题逐个与高考题比较. 确定复习策略的依据有两条:
一是高考的考试大纲(或《考试说明》),
二是自己的学生的实际情况。
因为复习工作的目的:
就是努力使自己的数学水平达到考试大纲的要求。
经常梳理自己的知识系统,结合自己学生的具体
情况制定数学复习策略,及时调整数学复习方法,
是每一位老师都需要重视的工作。
只有摸清自己学生的易忘、易错、易混点,
才能有的放矢地完善学科知识和能力结构,
明确复习重点。 (二)、学习考试说明,调整复习策略;第一轮复习:
老师是矛盾的主要方面,
高考的内容,要求是复习的主要依据第二轮复习:
学生是矛盾的主要方面,
学生尽可能努力适应高考的要求,
是复习工作的主要依据.第二轮复习:
真正让学生成为复习的主体,主动查漏补缺 :
老师应该:种好自己责任田,不占学生自留地指导学生回到课本:在第一轮复习后,
(1)每个章节都勾出一些课本题目,
要求人人过关。
(2)将解决这一些问题的通性通法,
常见的变形思路、方法
以及这部分的知识可能与哪些知识有联系.
印成讲义发给学生,
让学生对这章学习内容再作一次强化。保证人人得好基本分(三)、剖析重点章节,重视联系转化;综合运用能力的四个核心内容:
函数、数列、不等式和解析几何<1> “基本不等式”
<2>“平面向量的数量积”
<3>“同角三角函数的基本关系式”
<4>“两角和与差的正弦、余弦、正切”综合运用能力还涉及到的11个知识点<5>“等差数列” ;<6>“等比数列”
<7>“椭圆的标准方程和几何性质
<8>“双曲线的标准方程和几何性质
<9>“抛物线的标准方程和几何性质
<10>“函数的基本性质”
<11>“直线和平面垂直的判定和性质”1、强化练习讲评
第一、题组式讲评
练习中经常出现相似错误的题型或概念性题型,
常采用题组方式进行讲评,矫正出现的错误.
第二、发散式讲评
对于一些重要题型,常采用一题多解、一题多变
的方式进行讲评,培养求异思维,促进能力形成,
强化重点题型、重要方法的理解与领悟,起到触类
旁通的作用.
第三、收敛式讲评
对一些解法相同或相近题型常采用多题一解的收敛
方式进行讲评,讲评侧重对通性通法进行归纳,真
正起到“一把钥匙能开千把锁”的作用.(四)、研究通性通法,提高复习实效;2.从高考阅卷情况,看提高教学的实效
阅卷中发现考生存在的一些问题:
<1>“概念不清”;
<2>“推理过程混乱、不规范”;
<3>“计算能力较差”;
<4>“平面几何知识薄弱”等。做好回归课本与反思注重解题规范训练注重独立解题训练注重平面几何小、活、巧的结论应用3.注意四种数学思想方法的运用(1).函数方程思想
(2).分类讨论思想
(3).数形结合思想
(4).化归转化思想课例一:研究性问题1.y2=4x上有一条长为m的弦,求AB中点
横坐标的最小值.
2.x2=4y上的一部分恰好是高为4cm的酒
杯的横截面.要让半径为r冰球能够直接落
到酒杯的底部,求冰球半径r最大值.课例二:分类讨论问题知识背景 ---没有无缘无故的分类 1.为什么要分类讨论 例1.解不等式. 或或例1.解不等式. 例2.设函数
(Ⅰ)判断函数的奇偶数;
(Ⅱ)求函数的最小值.例3.已知轴截面的顶角为 ,母线长为 ,求经过两条母线的截面面积最大值.问题4解答:设两母线所成的角为把握分类依据---不重不漏 分类讨论问题1.为什么要分类讨论 2.如何进行分类讨论 例4.设函数
(Ⅰ)判断函数的奇偶数;
(Ⅱ)求函数的最小值.归纳要全面,不重也不漏例5.甲、乙两地相距1000公里,汽车运货物从甲地匀速运往乙地,为保证安全, 汽车的最高时速不得超过100公里,若汽车每小时的运输成本(以元为单位)由两部分组成: ⑴ 固定成本为100;
⑵ 可变成本部分与速度平方成正比例,比例系数是b(b>0);
为使全程运输成本最低,求汽车的行驶速度。解:假设行驶速度为v,y=固定成本+可变成本例5解答:有化有归例6. 设点P到M(-1,0)、
N(1,0)两点距离之差为2m,到x轴、y轴距离之比为2,求m的取值范围.分析(略)例7.某城市2001年末汽车保有量
为30万辆,预计此后每年报废上一
年末汽车保有量的6%,并且每年新
增汽车数量相同.为保护城市环境,
要求该城市汽车保有量不超过60万
辆,那么每年新增汽车数量不应超
过多少辆?解:设从2001年起每年的汽车保有量
则:……(1)当 时, 递增,要使
即只需 万辆
即
(2)当 时, 递减,
即 时,成立.
(3)当 时,
综上, 万时,满足要求.有化有归( 小 结 ) (1).知识背景----清 (2).分类依据----明 (3).不重不漏,有化有归 没有无缘无故的分类分类讨论问题3.把握分类的几个基本原则 欢迎老师们批评指正!以上个人主观意见,
难免有许多失之偏颇。再见!
同课章节目录
