苏科版七年级数学上册 3.6整式的加减课件(共18张PPT)
文档属性
| 名称 | 苏科版七年级数学上册 3.6整式的加减课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 36.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-12 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
3.6 整式的加减
第3章 代数式
教学目标
01
理解整式的加减的实质,掌握整式加减的一般步骤
02
熟练地进行整式的化简求值运算
整式的加减
b
a
b
b
a
b
b
a
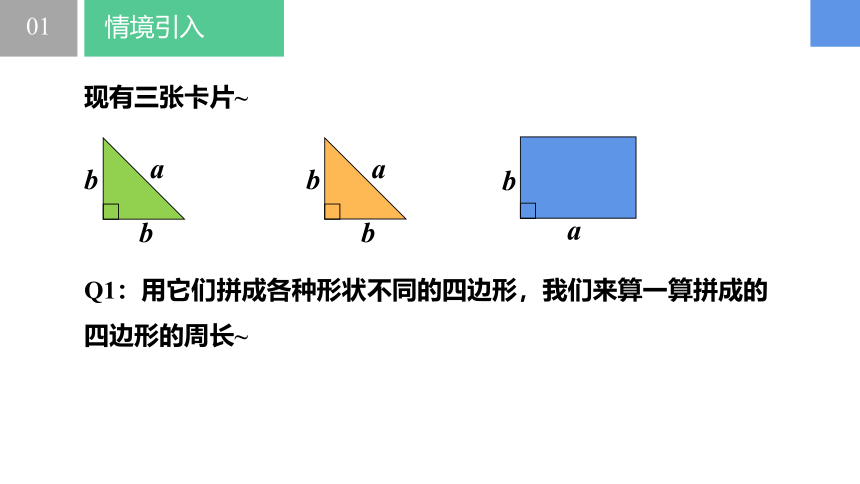
Q1:用它们拼成各种形状不同的四边形,我们来算一算拼成的四边形的周长~
现有三张卡片~
01
情境引入
b
a
a
a
a
b
b
b
b
a
a
a
b
b
b
b
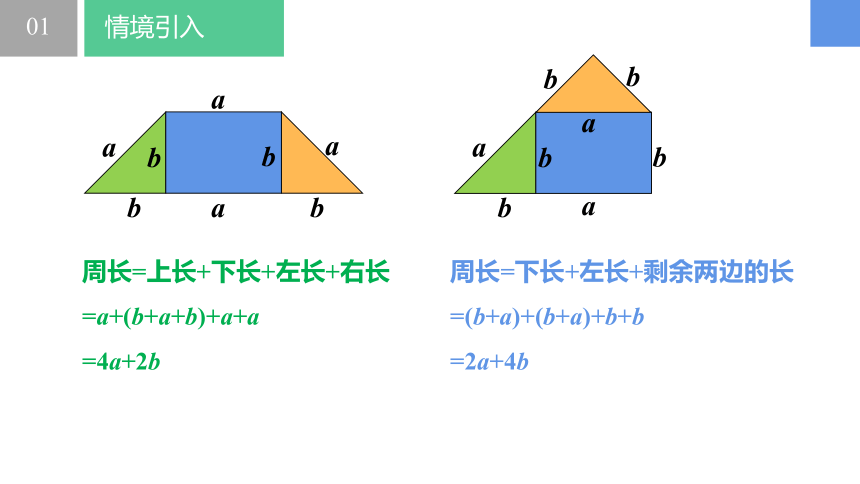
周长=上长+下长+左长+右长
=a+(b+a+b)+a+a
=4a+2b
周长=下长+左长+剩余两边的长
=(b+a)+(b+a)+b+b
=2a+4b
01
情境引入
Q2-1:这两个四边形周长的和是
Q2-2:这两个四边形周长的差是
两个四边形周长的和:
(4a+2b)+(2a+4b)
=6a+6b
01
情境引入
两个四边形周长的差:
(4a+2b)-(2a+4b)
=2a-2b
去括号、合并同类项,像这样的计算,就是整式的加减。
整式的加减的实质就是去括号、合并同类项。
02
知识精讲
整式加减的一般步骤:1.去括号;2.合并同类项。
整式的加减
例1、(1)已知A-2B=8a2-7ab,B=-4a2+6ab+7,求多项式A;
解:∵A-2B=8a2-7ab,B=-4a2+6ab+7,
∴A=2B+8a2-7ab
=2(-4a2+6ab+7)+8a2-7ab
=-8a2+12ab+14+8a2-7ab
=5ab+14。
03
典例精析
例1、(2)一个多项式与3a2-2a+1的和是多项式5a2-7a+2,求这个多项式。
解:设这个多项式为A,
由题意可知:A+(3a2-2a+1)=5a2-7a+2,
∴A=5a2-7a+2-(3a2-2a+1)
=5a2-7a+2-3a2+2a-1
=2a2-5a+1。
03
典例精析
例2、小优同学在计算一个多项式减去2x2-4x+5时,误以为加上此式,计算出错结果为-2x2+x-1,请你求出正确的答案。
解:法一:设这个多项式为A,
由题意可知:A+(2x2-4x+5)=-2x2+x-1,
∴A=-2x2+x-1-(2x2-4x+5)
=-2x2+x-1-2x2+4x-5
=-4x2+5x-6,
03
典例精析
A-(2x2-4x+5)
=-4x2+5x-6-(2x2-4x+5)
=-4x2+5x-6-2x2+4x-5
=-6x2+9x-11。
例2、小优同学在计算一个多项式减去2x2-4x+5时,误以为加上此式,计算出错结果为-2x2+x-1,请你求出正确的答案。
法二:设这个多项式为A,
由题意可知:A+(2x2-4x+5)=-2x2+x-1,
∴A=-2x2+x-1-(2x2-4x+5)
∴A-(2x2-4x+5)
=-2x2+x-1-2(2x2-4x+5)
=-2x2+x-1-4x2+8x-10
=-6x2+9x-11。
03
典例精析
整式的加减
—化简求值
例1、先化简,再求值:5(3a2b-ab2)-2(-ab2+4a2b),其中a=2,b=-3。
解:原式=15a2b-5ab2+2ab2-8a2b
=7a2b-3ab2,
将a=2,b=-3代入,
7a2b-3ab2
=7×22×(-3)-3×2×(-3)2
=-138。
先化简
后求值
03
典例精析
整式的加减—化简求值:
1.先化简:①去括号,②合并同类项;
2.后求值:将数值代入计算。
03
典例精析
例2、已知M=3a2+4ab-1,N=a2-2ab-1,
(1)用含a、b的代数式表示M-3N;
(2)若a、b满足(a-1)2+|b-2|=0,求M-3N的值。
03
典例精析
解:(1)M-3N
=3a2+4ab-1-3(a2-2ab-1)
=3a2+4ab-1-3a2+6ab+3
=10ab+2;
(2)∵(a-1)2+|b-2|=0,
∴a=1,b=2,
∴M-3N=10ab+2=10×1×2+2=22。
例3、先化简,再求值:已知8x2ay与-3x4y2+b是同类项,且A=a2+ab-2b2,B=3a2-ab-6b2,求2B-3(B-A)的值。
∵8x2ay与-3x4y2+b是同类项,
∴2a=4,1=2+b,
∴a=2,b=-1,
∴2B-3(B-A)=4ab=4×2×(-1)=-8。
解:2B-3(B-A)
=2B-3B+3A
=3A-B
=3(a2+ab-2b2)-(3a2-ab-6b2)
=3a2+3ab-6b2-3a2+ab+6b2
=4ab;
03
典例精析
课后总结
整式的加减—化简求值:
1.先化简:①去括号,②合并同类项;
2.后求值:将数值代入计算。
整式的加减的实质就是去括号、合并同类项。
整式加减的一般步骤:1.去括号;2.合并同类项。
3.6 整式的加减
3.6 整式的加减
第3章 代数式
教学目标
01
理解整式的加减的实质,掌握整式加减的一般步骤
02
熟练地进行整式的化简求值运算
整式的加减
b
a
b
b
a
b
b
a
Q1:用它们拼成各种形状不同的四边形,我们来算一算拼成的四边形的周长~
现有三张卡片~
01
情境引入
b
a
a
a
a
b
b
b
b
a
a
a
b
b
b
b
周长=上长+下长+左长+右长
=a+(b+a+b)+a+a
=4a+2b
周长=下长+左长+剩余两边的长
=(b+a)+(b+a)+b+b
=2a+4b
01
情境引入
Q2-1:这两个四边形周长的和是
Q2-2:这两个四边形周长的差是
两个四边形周长的和:
(4a+2b)+(2a+4b)
=6a+6b
01
情境引入
两个四边形周长的差:
(4a+2b)-(2a+4b)
=2a-2b
去括号、合并同类项,像这样的计算,就是整式的加减。
整式的加减的实质就是去括号、合并同类项。
02
知识精讲
整式加减的一般步骤:1.去括号;2.合并同类项。
整式的加减
例1、(1)已知A-2B=8a2-7ab,B=-4a2+6ab+7,求多项式A;
解:∵A-2B=8a2-7ab,B=-4a2+6ab+7,
∴A=2B+8a2-7ab
=2(-4a2+6ab+7)+8a2-7ab
=-8a2+12ab+14+8a2-7ab
=5ab+14。
03
典例精析
例1、(2)一个多项式与3a2-2a+1的和是多项式5a2-7a+2,求这个多项式。
解:设这个多项式为A,
由题意可知:A+(3a2-2a+1)=5a2-7a+2,
∴A=5a2-7a+2-(3a2-2a+1)
=5a2-7a+2-3a2+2a-1
=2a2-5a+1。
03
典例精析
例2、小优同学在计算一个多项式减去2x2-4x+5时,误以为加上此式,计算出错结果为-2x2+x-1,请你求出正确的答案。
解:法一:设这个多项式为A,
由题意可知:A+(2x2-4x+5)=-2x2+x-1,
∴A=-2x2+x-1-(2x2-4x+5)
=-2x2+x-1-2x2+4x-5
=-4x2+5x-6,
03
典例精析
A-(2x2-4x+5)
=-4x2+5x-6-(2x2-4x+5)
=-4x2+5x-6-2x2+4x-5
=-6x2+9x-11。
例2、小优同学在计算一个多项式减去2x2-4x+5时,误以为加上此式,计算出错结果为-2x2+x-1,请你求出正确的答案。
法二:设这个多项式为A,
由题意可知:A+(2x2-4x+5)=-2x2+x-1,
∴A=-2x2+x-1-(2x2-4x+5)
∴A-(2x2-4x+5)
=-2x2+x-1-2(2x2-4x+5)
=-2x2+x-1-4x2+8x-10
=-6x2+9x-11。
03
典例精析
整式的加减
—化简求值
例1、先化简,再求值:5(3a2b-ab2)-2(-ab2+4a2b),其中a=2,b=-3。
解:原式=15a2b-5ab2+2ab2-8a2b
=7a2b-3ab2,
将a=2,b=-3代入,
7a2b-3ab2
=7×22×(-3)-3×2×(-3)2
=-138。
先化简
后求值
03
典例精析
整式的加减—化简求值:
1.先化简:①去括号,②合并同类项;
2.后求值:将数值代入计算。
03
典例精析
例2、已知M=3a2+4ab-1,N=a2-2ab-1,
(1)用含a、b的代数式表示M-3N;
(2)若a、b满足(a-1)2+|b-2|=0,求M-3N的值。
03
典例精析
解:(1)M-3N
=3a2+4ab-1-3(a2-2ab-1)
=3a2+4ab-1-3a2+6ab+3
=10ab+2;
(2)∵(a-1)2+|b-2|=0,
∴a=1,b=2,
∴M-3N=10ab+2=10×1×2+2=22。
例3、先化简,再求值:已知8x2ay与-3x4y2+b是同类项,且A=a2+ab-2b2,B=3a2-ab-6b2,求2B-3(B-A)的值。
∵8x2ay与-3x4y2+b是同类项,
∴2a=4,1=2+b,
∴a=2,b=-1,
∴2B-3(B-A)=4ab=4×2×(-1)=-8。
解:2B-3(B-A)
=2B-3B+3A
=3A-B
=3(a2+ab-2b2)-(3a2-ab-6b2)
=3a2+3ab-6b2-3a2+ab+6b2
=4ab;
03
典例精析
课后总结
整式的加减—化简求值:
1.先化简:①去括号,②合并同类项;
2.后求值:将数值代入计算。
整式的加减的实质就是去括号、合并同类项。
整式加减的一般步骤:1.去括号;2.合并同类项。
3.6 整式的加减
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
