冀教版数学六年级下册第四、五单元综合素质达标卷(含答案)
文档属性
| 名称 | 冀教版数学六年级下册第四、五单元综合素质达标卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 470.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览




文档简介
第四、五单元综合素质达标
一、填空。 (每空 1 分,共 23 分)
1.7.5m3=( )dm3 108dm2=( ) m2
5.18L=( )L( )mL 8m360dm3=( )m3
2. 把一根长是 4m,底面半径是 2dm 的圆柱形木料截成 4 段相同的小圆柱,表面积比原来增加了( )dm2。
3. 右图是一个( ),3dm 是它的( ),10dm 是它的( ),它的体积是( )dm3,与它等底等高的圆柱的体积是( )dm3。
4. 一个圆柱形木料,底面半径是 3cm,高是 8cm,这个圆柱的表面积是 ( ) cm2。如果把它削成一个最大的圆锥,削去部分的体积是( )cm3。
5.从顶点沿着圆锥的高把一个圆锥切成完全相同的两部分, 切 面是一个底边长4cm、高 6cm 的等腰三角形,原来这个圆锥的体积是( )cm3。
6. 梦梦把右图这块长方体橡皮泥捏成一个高是 8cm 的圆柱,捏成的圆柱的底面积是( )cm2。如果捏成与圆柱底面相等的圆锥,这个圆锥的高是( )cm。 (橡皮泥无损耗)
7. 如图,这根圆木的底面直径是( )m。如果将这根圆木加工成最大的方木,方木的体积是( )m3,加工成的方木与原来圆木的体积比是( )。
8. 一个圆锥和一个圆柱的体积相等,圆锥和圆柱底面半径的比是 3:2,圆锥的高是16cm,圆柱的高是( )cm。
9.42118219751117061X 是某位老师的身份证号码,这是一位( )老师(填“男”或“女”) ,2024 年( )岁。
10. 如果密码锁的密码是由三个数字组成的,那么 0 ~ 9 这十个数字能组成( )个数字不重复的密码。
二、选择。 (将正确答案的字母填在括号里。每题 2 分,共 16 分)
1.营养学家建议,儿童每天水的摄入量约为 1500mL,要达到这个要求,明明每天用底面内直径为 8cm、高为 10cm 的圆柱形水杯喝水,他每天喝( )杯水比较合适。
A. 1 B. 2 C. 3 D. 7
2. 把一个正方体木块削成一个最大的圆柱,削去部分的体积约是正方体体积的( )。
A.80% B.78% C.78.5% D.21.5%
3.一桶饮料有1.57升,要分装到从里面量底面周长是 31.4厘米、高是 10 厘米的圆柱形水杯中,可以装满 ( )杯。
A. 1 B. 2 C. 3 D. 4
4.如图,用不同的方法将两个底面半径是 5 厘米,高是 10 厘米的圆柱切成相同的两部分,切开后( )的表面积之和比较大。
A. 甲 B. 乙
C. 一样大 D. 无法比较
5. 如图,把一个高是 4 厘米的圆柱切成若干等份,再拼成一个近似的长方体,表面积增加了 40 平方厘米。原来圆柱的侧面积是( ) 平方厘米。
A. 40 B. 62.8 C. 125.6 D. 502.4
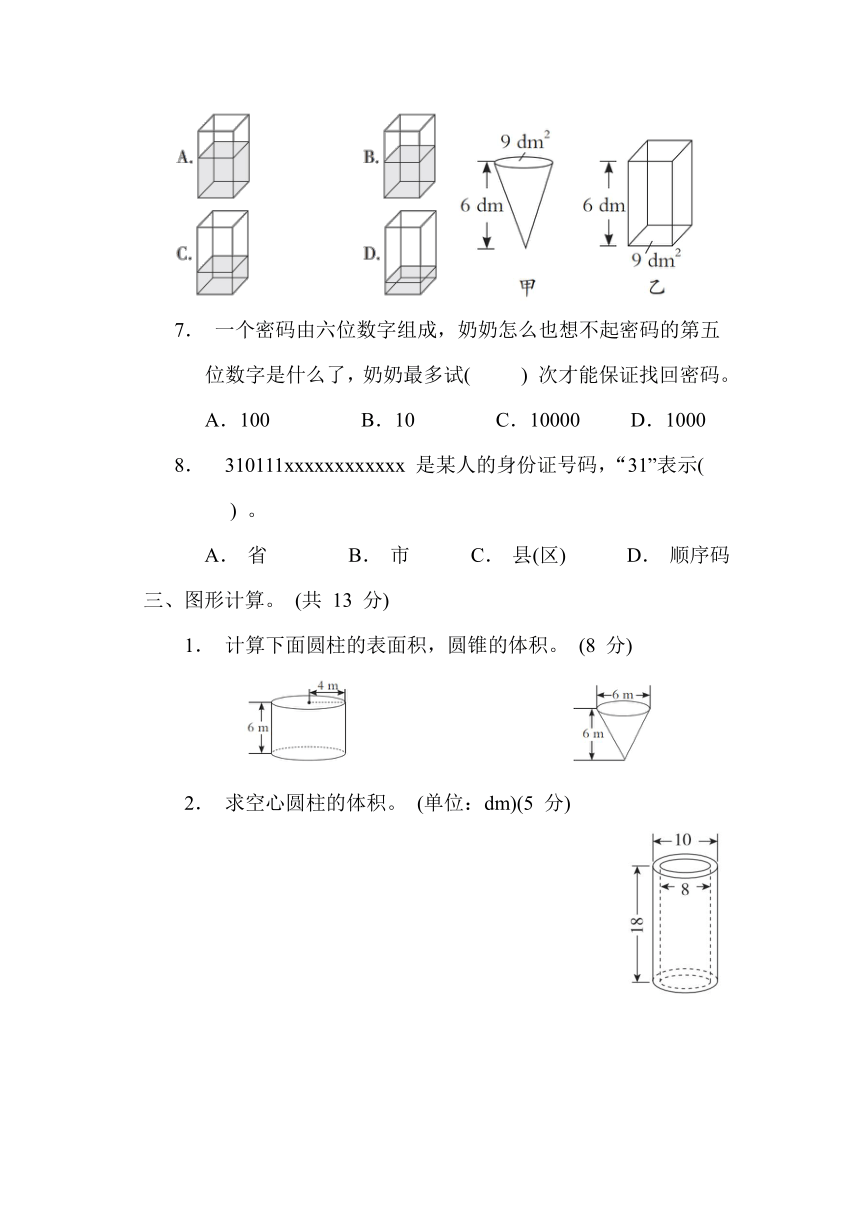
6. 如图,将甲容器中的水倒入乙容器中,下列表示倒入水后乙容器中的水位正确的是( ) 。
7. 一个密码由六位数字组成,奶奶怎么也想不起密码的第五位数字是什么了,奶奶最多试( ) 次才能保证找回密码。
A.100 B.10 C.10000 D.1000
8. 310111xxxxxxxxxxxx 是某人的身份证号码,“31”表示( ) 。
A. 省 B. 市 C. 县(区) D. 顺序码
三、图形计算。 (共 13 分)
1. 计算下面圆柱的表面积,圆锥的体积。 (8 分)
2. 求空心圆柱的体积。 (单位:dm)(5 分)
四、动手操作。 (8 分)
你能算出水面下降了多少厘米吗?
五、解决问题。 (共 40 分)
1.在“建筑中的美学”讲座上,明明和同学们了解到月亮门的相关知识。学校要在教学区和操场之间修一道厚度为25 cm 的围墙,原计划用土石 35m3,为了方便大家的通行,在围墙上多开了一个月亮门(如图所示) 。明明运用学到的数学知识,很快便计算出实际用了多少立方米土石。同学们,你们知道他是怎么算的吗?写一写吧! (5 分)
2. 人民广场上有两根高是2.5米,底面半径是0.5米的圆柱形花柱。在端午节来临之际,工作人员把花柱的侧面和顶部都用月季花装饰,计划平均每平方米插33朵月季花,插满两根花柱至少需要准备多少朵月季花?(得数保留整数)(5分)
3. 智慧农场要修建一个底面半径为 2 米、高为 2 米的圆柱形观赏水池,并且要在这个水池的底面和内壁贴上瓷砖。
(1)贴瓷砖部分的面积是多少平方米? (5 分)
(2) 建好后,向这个水池中注入水,水面高度为 1.8 米,一共向水池内注入了多少立方米的水? (瓷砖厚度忽略不计)(5 分)
4.【新情境】 龙卷风是一种强烈的涡旋现象, 常发生于夏季的雷雨天气,在下午至傍晚最为常见,影响范围虽小,但破坏力极大。某次龙卷风的高度约120米,顶部直径约100 米,那么这次龙卷风所形成的近似圆锥形空间的体积约为多少立方米? (6 分)
5. 一个圆柱形的容器,底面直径是 20cm,容器中装有一些水,水面离容器口 2cm,将一个高为 10cm 的圆锥形铁块完全浸没在水中后,有 50mL 的水溢出。这个圆锥形铁块的底面积是多少平方厘米? (6 分)
6. 航模小组制作了一个火箭助推器模型(如下图),它的上面是圆锥形, 下面是圆柱形。圆柱和圆锥的底面半径都是3cm,圆锥的高和圆柱的高都是 6cm。
(1) 要求火箭助推器模型的体积是多少立方厘米,下面是三位同学的做法,请在做法正确的同学名字后面的里打“√”。 (4 分)
(2)请你选择一种正确的方法,写出解题思路。 (4 分)
我选择的是( )的方法。
解题思路:
答案
一、 1.7500 5 180 8.06
2.75.36 3. 圆锥 底面半径 高 94.2 282.6
4. 207.24 150.72 5. 25.12
6. 9 24 7. 0.4 0.24 100 ∶ 157
8. 12 9. 男 49 10.720
二、 1.C 2.D 3.B 4.B
5.C 6.C 7.B 8.A
三、 1.3.14×42×2+3.14×4×2×6=251.2(m2)
×3.14×(6÷2) 2×6=56.52(m3)
2.3.14×[(10÷2) 2-(8÷2) 2]×18=508.68(dm3)
四、 ×40×6÷100=0.8(cm)
答: 水面下降了 0.8 cm。
五、 1.25 cm = 0.25 m
3.14×(2÷2) 2×0.25=0.785(m3)
35-0.785=34.215(m3)
答: 实际用了 34.215 m3 土石。
2.(2×3.14×0.5×2.5+3.14×0.5 2)×2×33 ≈ 570(朵)
答: 插满两根花柱至少需要准备 570 朵月季花。
3.(1)3.14×22+2×2×3.14×2=37.68(平方米)
答: 贴瓷砖部分的面积是 37.68 平方米。
(2)3.14×22×1.8=22.608(立方米)
答: 一共向水池内注入了 22.608 立方米的水。
4.× 3.14×(100÷2) 2×120=314000(立方米)
答: 这次龙卷风所形成的近似圆锥形空间的体积约为 314000 立方米。
5.50 mL=50cm3
[3.14×(20÷2) 2×2+50]×3÷10=203.4(cm2)
答: 这个圆锥形铁块的底面积是 203.4cm2。
6.(1)
(2)(答案不唯一) 蓝蓝
先求出圆柱的体积,再求出圆锥的体积,最后把它们的体积相加即可。
10/ 10
一、填空。 (每空 1 分,共 23 分)
1.7.5m3=( )dm3 108dm2=( ) m2
5.18L=( )L( )mL 8m360dm3=( )m3
2. 把一根长是 4m,底面半径是 2dm 的圆柱形木料截成 4 段相同的小圆柱,表面积比原来增加了( )dm2。
3. 右图是一个( ),3dm 是它的( ),10dm 是它的( ),它的体积是( )dm3,与它等底等高的圆柱的体积是( )dm3。
4. 一个圆柱形木料,底面半径是 3cm,高是 8cm,这个圆柱的表面积是 ( ) cm2。如果把它削成一个最大的圆锥,削去部分的体积是( )cm3。
5.从顶点沿着圆锥的高把一个圆锥切成完全相同的两部分, 切 面是一个底边长4cm、高 6cm 的等腰三角形,原来这个圆锥的体积是( )cm3。
6. 梦梦把右图这块长方体橡皮泥捏成一个高是 8cm 的圆柱,捏成的圆柱的底面积是( )cm2。如果捏成与圆柱底面相等的圆锥,这个圆锥的高是( )cm。 (橡皮泥无损耗)
7. 如图,这根圆木的底面直径是( )m。如果将这根圆木加工成最大的方木,方木的体积是( )m3,加工成的方木与原来圆木的体积比是( )。
8. 一个圆锥和一个圆柱的体积相等,圆锥和圆柱底面半径的比是 3:2,圆锥的高是16cm,圆柱的高是( )cm。
9.42118219751117061X 是某位老师的身份证号码,这是一位( )老师(填“男”或“女”) ,2024 年( )岁。
10. 如果密码锁的密码是由三个数字组成的,那么 0 ~ 9 这十个数字能组成( )个数字不重复的密码。
二、选择。 (将正确答案的字母填在括号里。每题 2 分,共 16 分)
1.营养学家建议,儿童每天水的摄入量约为 1500mL,要达到这个要求,明明每天用底面内直径为 8cm、高为 10cm 的圆柱形水杯喝水,他每天喝( )杯水比较合适。
A. 1 B. 2 C. 3 D. 7
2. 把一个正方体木块削成一个最大的圆柱,削去部分的体积约是正方体体积的( )。
A.80% B.78% C.78.5% D.21.5%
3.一桶饮料有1.57升,要分装到从里面量底面周长是 31.4厘米、高是 10 厘米的圆柱形水杯中,可以装满 ( )杯。
A. 1 B. 2 C. 3 D. 4
4.如图,用不同的方法将两个底面半径是 5 厘米,高是 10 厘米的圆柱切成相同的两部分,切开后( )的表面积之和比较大。
A. 甲 B. 乙
C. 一样大 D. 无法比较
5. 如图,把一个高是 4 厘米的圆柱切成若干等份,再拼成一个近似的长方体,表面积增加了 40 平方厘米。原来圆柱的侧面积是( ) 平方厘米。
A. 40 B. 62.8 C. 125.6 D. 502.4
6. 如图,将甲容器中的水倒入乙容器中,下列表示倒入水后乙容器中的水位正确的是( ) 。
7. 一个密码由六位数字组成,奶奶怎么也想不起密码的第五位数字是什么了,奶奶最多试( ) 次才能保证找回密码。
A.100 B.10 C.10000 D.1000
8. 310111xxxxxxxxxxxx 是某人的身份证号码,“31”表示( ) 。
A. 省 B. 市 C. 县(区) D. 顺序码
三、图形计算。 (共 13 分)
1. 计算下面圆柱的表面积,圆锥的体积。 (8 分)
2. 求空心圆柱的体积。 (单位:dm)(5 分)
四、动手操作。 (8 分)
你能算出水面下降了多少厘米吗?
五、解决问题。 (共 40 分)
1.在“建筑中的美学”讲座上,明明和同学们了解到月亮门的相关知识。学校要在教学区和操场之间修一道厚度为25 cm 的围墙,原计划用土石 35m3,为了方便大家的通行,在围墙上多开了一个月亮门(如图所示) 。明明运用学到的数学知识,很快便计算出实际用了多少立方米土石。同学们,你们知道他是怎么算的吗?写一写吧! (5 分)
2. 人民广场上有两根高是2.5米,底面半径是0.5米的圆柱形花柱。在端午节来临之际,工作人员把花柱的侧面和顶部都用月季花装饰,计划平均每平方米插33朵月季花,插满两根花柱至少需要准备多少朵月季花?(得数保留整数)(5分)
3. 智慧农场要修建一个底面半径为 2 米、高为 2 米的圆柱形观赏水池,并且要在这个水池的底面和内壁贴上瓷砖。
(1)贴瓷砖部分的面积是多少平方米? (5 分)
(2) 建好后,向这个水池中注入水,水面高度为 1.8 米,一共向水池内注入了多少立方米的水? (瓷砖厚度忽略不计)(5 分)
4.【新情境】 龙卷风是一种强烈的涡旋现象, 常发生于夏季的雷雨天气,在下午至傍晚最为常见,影响范围虽小,但破坏力极大。某次龙卷风的高度约120米,顶部直径约100 米,那么这次龙卷风所形成的近似圆锥形空间的体积约为多少立方米? (6 分)
5. 一个圆柱形的容器,底面直径是 20cm,容器中装有一些水,水面离容器口 2cm,将一个高为 10cm 的圆锥形铁块完全浸没在水中后,有 50mL 的水溢出。这个圆锥形铁块的底面积是多少平方厘米? (6 分)
6. 航模小组制作了一个火箭助推器模型(如下图),它的上面是圆锥形, 下面是圆柱形。圆柱和圆锥的底面半径都是3cm,圆锥的高和圆柱的高都是 6cm。
(1) 要求火箭助推器模型的体积是多少立方厘米,下面是三位同学的做法,请在做法正确的同学名字后面的里打“√”。 (4 分)
(2)请你选择一种正确的方法,写出解题思路。 (4 分)
我选择的是( )的方法。
解题思路:
答案
一、 1.7500 5 180 8.06
2.75.36 3. 圆锥 底面半径 高 94.2 282.6
4. 207.24 150.72 5. 25.12
6. 9 24 7. 0.4 0.24 100 ∶ 157
8. 12 9. 男 49 10.720
二、 1.C 2.D 3.B 4.B
5.C 6.C 7.B 8.A
三、 1.3.14×42×2+3.14×4×2×6=251.2(m2)
×3.14×(6÷2) 2×6=56.52(m3)
2.3.14×[(10÷2) 2-(8÷2) 2]×18=508.68(dm3)
四、 ×40×6÷100=0.8(cm)
答: 水面下降了 0.8 cm。
五、 1.25 cm = 0.25 m
3.14×(2÷2) 2×0.25=0.785(m3)
35-0.785=34.215(m3)
答: 实际用了 34.215 m3 土石。
2.(2×3.14×0.5×2.5+3.14×0.5 2)×2×33 ≈ 570(朵)
答: 插满两根花柱至少需要准备 570 朵月季花。
3.(1)3.14×22+2×2×3.14×2=37.68(平方米)
答: 贴瓷砖部分的面积是 37.68 平方米。
(2)3.14×22×1.8=22.608(立方米)
答: 一共向水池内注入了 22.608 立方米的水。
4.× 3.14×(100÷2) 2×120=314000(立方米)
答: 这次龙卷风所形成的近似圆锥形空间的体积约为 314000 立方米。
5.50 mL=50cm3
[3.14×(20÷2) 2×2+50]×3÷10=203.4(cm2)
答: 这个圆锥形铁块的底面积是 203.4cm2。
6.(1)
(2)(答案不唯一) 蓝蓝
先求出圆柱的体积,再求出圆锥的体积,最后把它们的体积相加即可。
10/ 10
