北师大版七年级数学上册3.4整式的加减 课件(共22张PPT)
文档属性
| 名称 | 北师大版七年级数学上册3.4整式的加减 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 506.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-12 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
北师大版 数学 七年级上册
4 整式的加减
第三章 整式及其加减
学习目标
1.进一步经历用字母表示数量关系的过程,发展符号感.(重点)
2.灵活准确的运用整式的加减的步骤进行运算.(难点)
一、导入新课
复习回顾
3.化简:(1)4(x+2x2-5)+(-2x-x2+1); (2)-5(x2-2x-3)-3(3x2+5);
解:(1)原式=4x+8x2-20-2x-x2+1
=7x2+2x-19.
(2)原式=-(5x2-10x-15)-(9x2+15)
=-5x2+10x+15-9x2-15
=-14x2+10x.
1.合并同类项法则:合并同类项时,把同类项的 相加,字母和字母的 不变.
2.去括号法则:括号前是“+”号,把括号和它前面的“+”号去掉后,原括号里各项的符号__________;括号前是“-”号,把括号和它前面的“-”号去掉后,原括号里各项的符号__________.
都不改变
都要改变
系数
指数
一、导入新课
情境导入
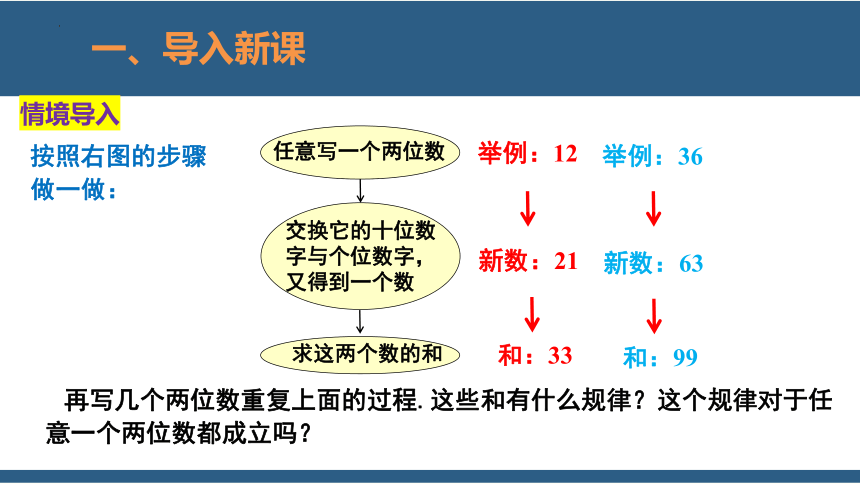
再写几个两位数重复上面的过程.这些和有什么规律?这个规律对于任意一个两位数都成立吗?
举例:12
举例:36
新数:21
和:33
新数:63
和:99
任意写一个两位数
交换它的十位数字与个位数字,又得到一个数
求这两个数的和
按照右图的步骤做一做:
二、新知探究
如果用a,b分别表示一个两位数的十位数字和个位数字,那么这个两位数可以表示为: .交换这个两位数的十位数字和个位数字,得到的数是: .将这两个数相加:
+ =
.
10a+b+10b+a=11a+11b=11(a+b)
10a+b
10b+a
(10a+b)
(10b+a)
结论:
这些和都是11的倍数.
探究一:整式的加减
二、新知探究
做一做
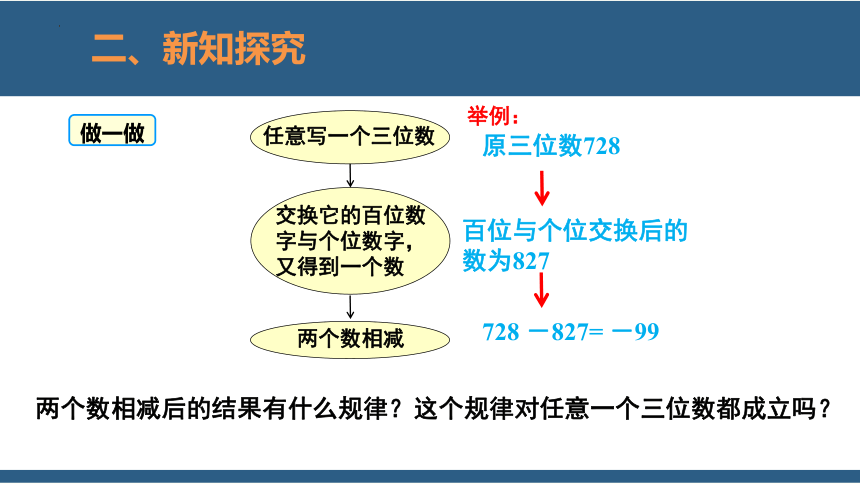
任意写一个三位数
交换它的百位数字与个位数字,又得到一个数
两个数相减
两个数相减后的结果有什么规律?这个规律对任意一个三位数都成立吗?
原三位数728
举例:
百位与个位交换后的数为827
728 -827= -99
如果用a,b,c分别表示一个三位数的百位数字、十位数字和个位数字,那么这个三位数可以表示为: .交换这个三位数的百位数字和个位数字,得到的数是: .将这两个数相减: - .
二、新知探究
100a+10b+c
100c+10b+a
(100a+10b+c) ( 100c+10b+a)
(100a+10b+c)-( 100c+10b+a)
= 100a+10b+c-100c-10b-a
=99a-99c
=99(a-c).
结论:
原三位数与交换后的三位数之差是99的倍数.
利用整式的加减运算很容易解释其中的规律
=?
议一议
在上面的两个问题中,分别涉及了整式的什么运算?说说你是如何运算的?
二、新知探究
合并同类项
去括号
整式的加减运算
二、新知探究
解:(1)(2x2-3x+1)+(-3x2+5x-7)
=2x2-3x2-3x+5x+1-7
=-x2+2x-6.
(2)
计算:
跟踪练习1
二、新知探究
知识归纳
通过上面的学习,你能得到整式加减的运算法则吗?
进行整式加减运算时,如果有括号要先去括号,再合并同类项.
对整式加减运算的结果的要求:
(1)结果中不能再含有同类项;
(2)结果中不能再含有括号.
解:(1)原式=6a2b-3ab2-4ab2+12a2b
=18a2b-7ab2.
二、新知探究
跟踪练习2
(2)原式=-3x2+6x+3x2-4x-1
=2x-1.
二、新知探究
做一做
先对整式去括号、合并同类项,再将字母的值代入化简后的代数式中求值.
做大小两个长方体纸盒,尺寸如下(单位:cm):
(1)做这两个纸盒共用料多少?
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
(1)做这两个纸盒共用料= (2ab+2bc+2ca)+(6ab+8bc+6ca)
=2ab+2bc+2ca+6ab+8bc+6ca
=(8ab+10bc+8ca) (cm2 ).
a
b
c
1.5a
2b
2c
解:小纸盒的表面积是( )cm2
2ab
+2bc
+2ca
大纸盒的表面积是( )cm2
6ab
+ 8bc
+ 6ca
探究二:整式加减的应用
二、新知探究
(2)做大纸盒比做小纸盒多用料
(6ab+8bc+6ca)- (2ab+2bc+2ca)
=6ab+8bc+6ca-2ab-2bc-2ca
=(4ab+6bc+4ca)(cm2)
(2)做大纸盒比小纸盒多用料多少平方厘米?
a
b
c
1.5a
2b
2c
二、新知探究
三、典例精析
解:(1)(2x2-3x-1)+(-x2+3x-5)
=2x2-3x-1-x2+3x-5
=x2-6.
(2)原式=-2mn+6m2-m2+5mn-5m2-2mn
=mn.
三、典例精析
四、当堂练习
1.计算x-2(y-z)的结果是( )
A.x-2y-z B.x-2y-2z
C.x-2y+2z D.x+2y-2z
2.若A和B都是五次多项式,则A+B一定是( )
A.十次多项式 B.五次多项式
C.次数不高于5的整式 D.次数不低于5的多项式
C
C
四、当堂练习
3.10a-5减去(-5a+7)的结果是________.
15a-12
4.计算:(1)(3a2+b2-5ab)+(4ab-b2+7a2)=__________;
(2)-(m-2n)-(-m+n)=________.
10a2-ab
n
5.已知A=a2-ab,B=ab+b2,则A+B=________,
A-B=____________,3A-2B=_______________.
a2+b2
a2-2ab-b2
3a2-5ab-2b2
四、当堂练习
6.计算:(1)3b+5a-(2a-4b);(2)4a3-(7ab-1)+2(3ab-2a3).
解:(1)原式=3b+5a-2a+4b
=3a+7b.
(2)原式=4a3-7ab+1+6ab-4a3
=1-ab.
四、当堂练习
7.先化简,再求值:5a2+3b2+2(a2-b2)-(5a2-3b2),其中a为最大的负整数,b为2的倒数.
由a为最大的负整数,b为2的倒数,得a=-1,b=.5a2+3b2+2(a2-b2)-(5a2-3b2)=5a2+3b2+2a2-2b2-5a2+3b2=2a2+4b2.当a=-1,b=时,原式=2×(-1)2+4×=2+1=3.
五、课堂小结
整式加减的步骤
整式加减的应用
整式的加减
去括号
合并同类项
六、作业布置
习题3.7
北师大版 数学 七年级上册
4 整式的加减
第三章 整式及其加减
学习目标
1.进一步经历用字母表示数量关系的过程,发展符号感.(重点)
2.灵活准确的运用整式的加减的步骤进行运算.(难点)
一、导入新课
复习回顾
3.化简:(1)4(x+2x2-5)+(-2x-x2+1); (2)-5(x2-2x-3)-3(3x2+5);
解:(1)原式=4x+8x2-20-2x-x2+1
=7x2+2x-19.
(2)原式=-(5x2-10x-15)-(9x2+15)
=-5x2+10x+15-9x2-15
=-14x2+10x.
1.合并同类项法则:合并同类项时,把同类项的 相加,字母和字母的 不变.
2.去括号法则:括号前是“+”号,把括号和它前面的“+”号去掉后,原括号里各项的符号__________;括号前是“-”号,把括号和它前面的“-”号去掉后,原括号里各项的符号__________.
都不改变
都要改变
系数
指数
一、导入新课
情境导入
再写几个两位数重复上面的过程.这些和有什么规律?这个规律对于任意一个两位数都成立吗?
举例:12
举例:36
新数:21
和:33
新数:63
和:99
任意写一个两位数
交换它的十位数字与个位数字,又得到一个数
求这两个数的和
按照右图的步骤做一做:
二、新知探究
如果用a,b分别表示一个两位数的十位数字和个位数字,那么这个两位数可以表示为: .交换这个两位数的十位数字和个位数字,得到的数是: .将这两个数相加:
+ =
.
10a+b+10b+a=11a+11b=11(a+b)
10a+b
10b+a
(10a+b)
(10b+a)
结论:
这些和都是11的倍数.
探究一:整式的加减
二、新知探究
做一做
任意写一个三位数
交换它的百位数字与个位数字,又得到一个数
两个数相减
两个数相减后的结果有什么规律?这个规律对任意一个三位数都成立吗?
原三位数728
举例:
百位与个位交换后的数为827
728 -827= -99
如果用a,b,c分别表示一个三位数的百位数字、十位数字和个位数字,那么这个三位数可以表示为: .交换这个三位数的百位数字和个位数字,得到的数是: .将这两个数相减: - .
二、新知探究
100a+10b+c
100c+10b+a
(100a+10b+c) ( 100c+10b+a)
(100a+10b+c)-( 100c+10b+a)
= 100a+10b+c-100c-10b-a
=99a-99c
=99(a-c).
结论:
原三位数与交换后的三位数之差是99的倍数.
利用整式的加减运算很容易解释其中的规律
=?
议一议
在上面的两个问题中,分别涉及了整式的什么运算?说说你是如何运算的?
二、新知探究
合并同类项
去括号
整式的加减运算
二、新知探究
解:(1)(2x2-3x+1)+(-3x2+5x-7)
=2x2-3x2-3x+5x+1-7
=-x2+2x-6.
(2)
计算:
跟踪练习1
二、新知探究
知识归纳
通过上面的学习,你能得到整式加减的运算法则吗?
进行整式加减运算时,如果有括号要先去括号,再合并同类项.
对整式加减运算的结果的要求:
(1)结果中不能再含有同类项;
(2)结果中不能再含有括号.
解:(1)原式=6a2b-3ab2-4ab2+12a2b
=18a2b-7ab2.
二、新知探究
跟踪练习2
(2)原式=-3x2+6x+3x2-4x-1
=2x-1.
二、新知探究
做一做
先对整式去括号、合并同类项,再将字母的值代入化简后的代数式中求值.
做大小两个长方体纸盒,尺寸如下(单位:cm):
(1)做这两个纸盒共用料多少?
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
(1)做这两个纸盒共用料= (2ab+2bc+2ca)+(6ab+8bc+6ca)
=2ab+2bc+2ca+6ab+8bc+6ca
=(8ab+10bc+8ca) (cm2 ).
a
b
c
1.5a
2b
2c
解:小纸盒的表面积是( )cm2
2ab
+2bc
+2ca
大纸盒的表面积是( )cm2
6ab
+ 8bc
+ 6ca
探究二:整式加减的应用
二、新知探究
(2)做大纸盒比做小纸盒多用料
(6ab+8bc+6ca)- (2ab+2bc+2ca)
=6ab+8bc+6ca-2ab-2bc-2ca
=(4ab+6bc+4ca)(cm2)
(2)做大纸盒比小纸盒多用料多少平方厘米?
a
b
c
1.5a
2b
2c
二、新知探究
三、典例精析
解:(1)(2x2-3x-1)+(-x2+3x-5)
=2x2-3x-1-x2+3x-5
=x2-6.
(2)原式=-2mn+6m2-m2+5mn-5m2-2mn
=mn.
三、典例精析
四、当堂练习
1.计算x-2(y-z)的结果是( )
A.x-2y-z B.x-2y-2z
C.x-2y+2z D.x+2y-2z
2.若A和B都是五次多项式,则A+B一定是( )
A.十次多项式 B.五次多项式
C.次数不高于5的整式 D.次数不低于5的多项式
C
C
四、当堂练习
3.10a-5减去(-5a+7)的结果是________.
15a-12
4.计算:(1)(3a2+b2-5ab)+(4ab-b2+7a2)=__________;
(2)-(m-2n)-(-m+n)=________.
10a2-ab
n
5.已知A=a2-ab,B=ab+b2,则A+B=________,
A-B=____________,3A-2B=_______________.
a2+b2
a2-2ab-b2
3a2-5ab-2b2
四、当堂练习
6.计算:(1)3b+5a-(2a-4b);(2)4a3-(7ab-1)+2(3ab-2a3).
解:(1)原式=3b+5a-2a+4b
=3a+7b.
(2)原式=4a3-7ab+1+6ab-4a3
=1-ab.
四、当堂练习
7.先化简,再求值:5a2+3b2+2(a2-b2)-(5a2-3b2),其中a为最大的负整数,b为2的倒数.
由a为最大的负整数,b为2的倒数,得a=-1,b=.5a2+3b2+2(a2-b2)-(5a2-3b2)=5a2+3b2+2a2-2b2-5a2+3b2=2a2+4b2.当a=-1,b=时,原式=2×(-1)2+4×=2+1=3.
五、课堂小结
整式加减的步骤
整式加减的应用
整式的加减
去括号
合并同类项
六、作业布置
习题3.7
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
