贵州省贵阳市普通中学2014-2015学年高一上学期期末监测数学试题(word版)
文档属性
| 名称 | 贵州省贵阳市普通中学2014-2015学年高一上学期期末监测数学试题(word版) |

|
|
| 格式 | zip | ||
| 文件大小 | 567.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-27 00:00:00 | ||
图片预览


文档简介
贵阳市普通中学2014—2015学年度第一学期期末监测考试试卷
高一数学
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则( )。
A. B. C. D.
2. 函数是( )。
A.周期为的奇函数 B. 周期为的偶函数
C.周期为的偶函数 D.周期为的奇函数
3. 已知向量,,且,则
A. B. C. D.
4.函数的图像恒过定点为( )。
A. B. C. D.
5.已知,则三者的大小关系是( )。
A. B. C. D.
6.已知,则的值为( )。
A. B. C. D.
7.已知函数,则的值是( )。
A. B. C. D.
若向量满足: ,且则与的夹角是( )。
A. B. C. D.
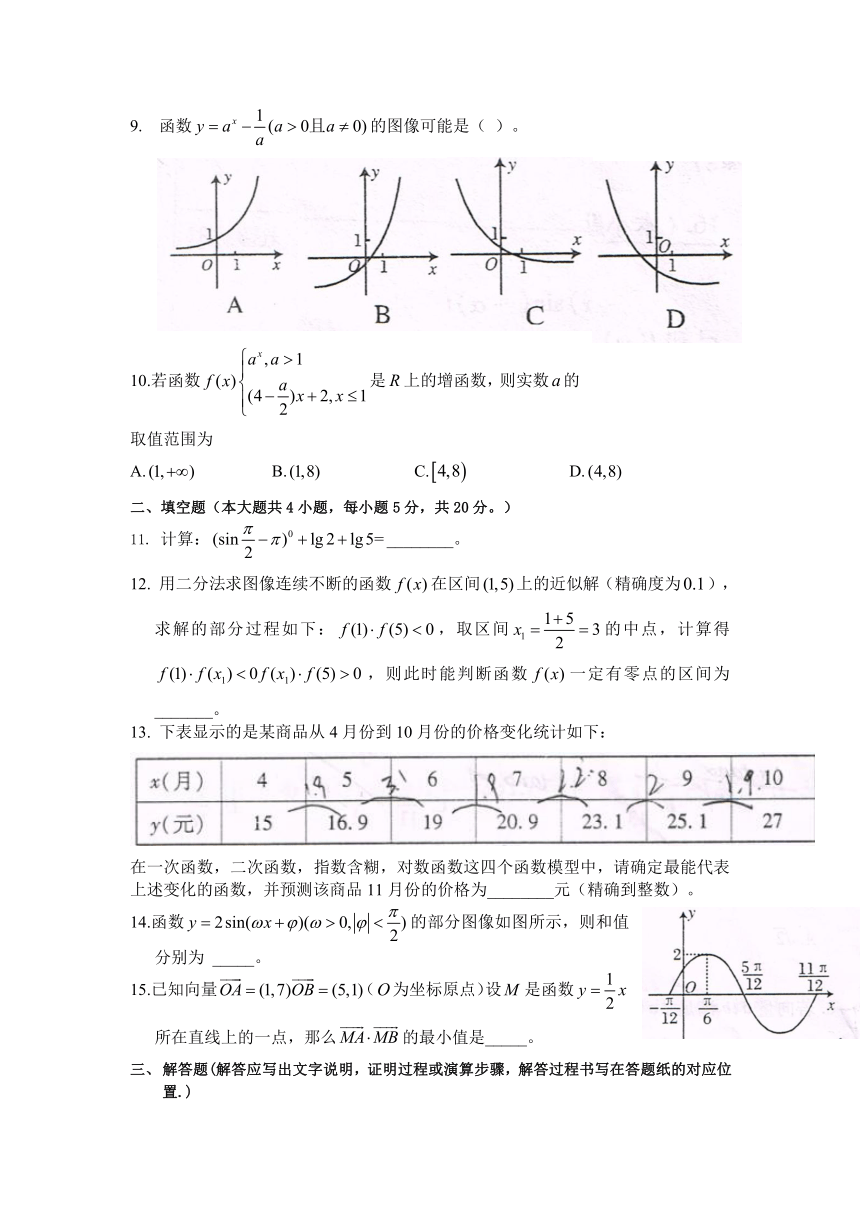
9. 函数的图像可能是( )。
10.若函数是上的增函数,则实数的取值范围为
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分。)
11. 计算:________。
12. 用二分法求图像连续不断的函数在区间上的近似解(精确度为),求解的部分过程如下:,取区间的中点,计算得,则此时能判断函数一定有零点的区间为_______。
13. 下表显示的是某商品从4月份到10月份的价格变化统计如下:
在一次函数,二次函数,指数含糊,对数函数这四个函数模型中,请确定最能代表上述变化的函数,并预测该商品11月份的价格为________元(精确到整数)。
14.函数的部分图像如图所示,则和值分别为 _____。
15.已知向量(为坐标原点)设是函数所在直线上的一点,那么的最小值是_____。
解答题(解答应写出文字说明,证明过程或演算步骤,解答过程书写在答题纸的对应位置.)
16.(本小题满分8分)
已知。
化简。
若为第三象限角,且,求的值
17. (本小题满分8分)
在梯形中,,分别是的中点,设。
在图上作出向量(不要求写出作法)
请将用表示。
18(本小题满分8分)
已知函数,设。
求函数的定义域
判断函数的奇偶性,并说明理由
19. (本小题满分8分)
已知。
若,求的值;
设函数,求函数的最大值及相应的的值
20. (本小题满分8分)
已知二次函数且其图像的顶点恰好在函数的图像上。
求函数的解析式
若函数恰有两个零点,求的取值范围。
高一数学
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合,则( )。
A. B. C. D.
2. 函数是( )。
A.周期为的奇函数 B. 周期为的偶函数
C.周期为的偶函数 D.周期为的奇函数
3. 已知向量,,且,则
A. B. C. D.
4.函数的图像恒过定点为( )。
A. B. C. D.
5.已知,则三者的大小关系是( )。
A. B. C. D.
6.已知,则的值为( )。
A. B. C. D.
7.已知函数,则的值是( )。
A. B. C. D.
若向量满足: ,且则与的夹角是( )。
A. B. C. D.
9. 函数的图像可能是( )。
10.若函数是上的增函数,则实数的取值范围为
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分。)
11. 计算:________。
12. 用二分法求图像连续不断的函数在区间上的近似解(精确度为),求解的部分过程如下:,取区间的中点,计算得,则此时能判断函数一定有零点的区间为_______。
13. 下表显示的是某商品从4月份到10月份的价格变化统计如下:
在一次函数,二次函数,指数含糊,对数函数这四个函数模型中,请确定最能代表上述变化的函数,并预测该商品11月份的价格为________元(精确到整数)。
14.函数的部分图像如图所示,则和值分别为 _____。
15.已知向量(为坐标原点)设是函数所在直线上的一点,那么的最小值是_____。
解答题(解答应写出文字说明,证明过程或演算步骤,解答过程书写在答题纸的对应位置.)
16.(本小题满分8分)
已知。
化简。
若为第三象限角,且,求的值
17. (本小题满分8分)
在梯形中,,分别是的中点,设。
在图上作出向量(不要求写出作法)
请将用表示。
18(本小题满分8分)
已知函数,设。
求函数的定义域
判断函数的奇偶性,并说明理由
19. (本小题满分8分)
已知。
若,求的值;
设函数,求函数的最大值及相应的的值
20. (本小题满分8分)
已知二次函数且其图像的顶点恰好在函数的图像上。
求函数的解析式
若函数恰有两个零点,求的取值范围。
同课章节目录
