北京市延庆县2014-2015学年高一数学上学期1月期末考试数学试题及答案
文档属性
| 名称 | 北京市延庆县2014-2015学年高一数学上学期1月期末考试数学试题及答案 |  | |
| 格式 | zip | ||
| 文件大小 | 201.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-27 19:49:52 | ||
图片预览



文档简介
北京市延庆县2014-2015学年高一数学上学期1月期末考试数学试题及答案 2015.1
满分共150分。考试时间120分钟。
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集,集合,,则
A.
B.
C.
D.
2.已知,与角终边相同的角是
A.
B.
C.
D.
3.若 ,且 ,则角是
A.第一象限角
B.第二象限角
C.第三象限角
D.第四象限角
4.若角的终边经过点,则
A.
B.
C.
D.
5.函数的定义域为
A.
B.
C.
D.
6.已知向量,那么向量的坐标是
A.
B.
C.
D.
7.函数的图像过定点
A.
B.
C.
D.
8.若,则的值为
A.
B.
C.
D.
9.设A、B、C是三角形的三个内角,下列关系恒成立的是
A.
B.
C.
D.
10.已知向量,满足,且则与的夹角为
A.
B.
C.
D.
11. 要得到的图象只需将的图象
A.向左平移个单位
B.向右平移个单位
C.向右平移个单位
D.向左平移个单位
12.已知函数是定义在上的偶函数,且在区间上单调递增,若实数满足,则的取值范围是
A.
B.
C.
D.
二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在题中横线上.
13.不等式的解集为____ ___.
14.已知,则______.
15.已知向量,若,则_____;若,则_____.
16.已知是圆上两点,弧度,,则劣弧长度是__ ____.
17.已知,则大小关系是_____ __.
18.设函数,若对任意,存在x1,x2使恒成立,则的最小值是_______.
三、解答题:本大题共6小题,共60分. 解答应写出文字说明,证明过程或演算步骤 .
19.(本题8分)求下列各式的植:
(Ⅰ);
(Ⅱ) .
解:
20.(本题8分)设全集为,集合,.
(Ⅰ)若,求;
(Ⅱ)若,求实数的取值范围.
解:
21.(本题10分)设函数.
(Ⅰ)求函数的定义域;
(Ⅱ)已知,且,求的值.
解:
22.(本题10分)已知函数.
(Ⅰ)求的最小正周期;
(Ⅱ)求函数的单调减区间;
(Ⅲ)当时,求函数的最小值.
解:
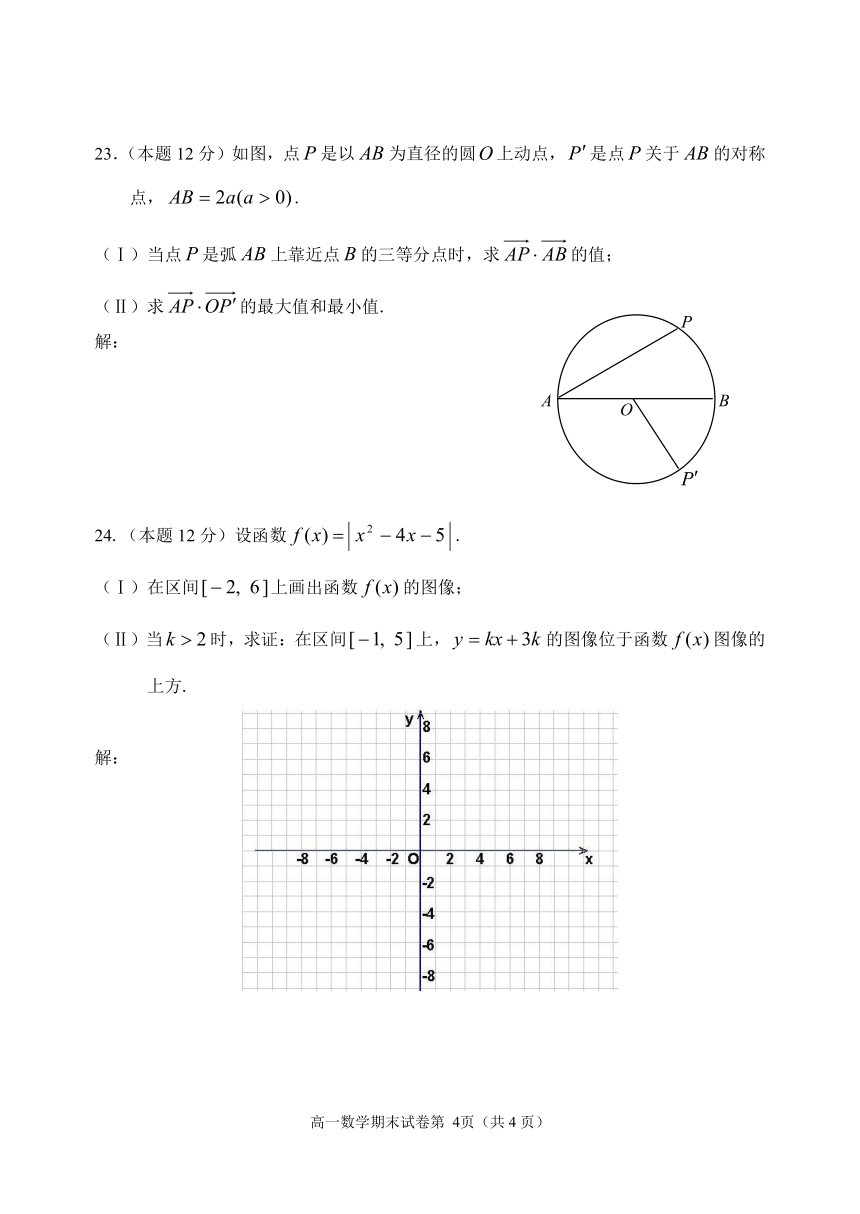
23.(本题12分)如图,点是以为直径的圆上动点,是点关于的对称点,.
(Ⅰ)当点是弧上靠近点的三等分点时,求的值;
(Ⅱ)求的最大值和最小值.
解:
24.(本题12分)设函数.
(Ⅰ)在区间上画出函数的图像;
(Ⅱ)当时,求证:在区间上,的图像位于函数图像的上方.
解:
延庆县2014—2015学年度第一学期期末考试参考答案
高一数学 2015.1
一、选择题(本大题共12小题,每小题5分,共60分.)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
B
C
B
D
C
C
A
B
D
A
二、填空题(本大题共6小题,每小题5分,共30分.)
13. 14. 15.; 16. 17. 18.
三、解答题:本大题共6小题,共60分. 解答应写出文字说明,证明过程或演算步骤 .
19.(本题8分)
解:(Ⅰ)原式. ………………………………4分
(Ⅱ)原式. …………………8分
20.(本题8分)
解:(Ⅰ)当时,,或,
∴. ………………………………4分
(Ⅱ)若,则,∴或,解得或.
∴实数的取值范围. …………………………………8分
21.(本题10分)
解:(Ⅰ)要使函数有意义,只要使,
∴函数的定义域为且. ………………3分
(Ⅱ)由,得,∴. …………5分
∵,∴. ………………7分
∴
. ………………10分
22.(本题10分)
解:(Ⅰ)∵
, ……………………2分
∴的最小正周期. ……………………4分
(Ⅱ)由得
∴函数的单调减区间. …………………7分
(Ⅲ)由.
∴当时,即时,取得最小值. …………10分
23.(本题12分)
解法一:(Ⅰ)连接,,
∵是弧靠近点的三等分点,
∴. ……………………2分
∴ ………………………4分
(Ⅱ)设, 则,
此时向量与的夹角为, ………………………6分
∴
, ………………………10分
∴ 当时,的最小值为.
当时,的最大值为. ………………12分
解法二:(Ⅰ)以直径所在直线为轴,以为坐标原点建立平面直角坐标系.
∵是弧靠近点的三等分点,连接,则, …………1分
∴点坐标为. …………2分
又点坐标是,点坐标是,
∴,,
∴. …………4分
(Ⅱ)设,,则,
∴,. ………………6分
∴
. ………10分
当时,有最小值,
当时,有最大值. …………………12分
24.(本题12分)
解]:(Ⅰ)
…………………………3分
(Ⅱ)当时,.
, ………………………5分
∵ ,∴. ………………………6分
① 当,即时,取,
.
∵ ,∴ 则.………9分
② 当,即时,取,=.
由 ①、②可知,当时,在上,
∴在区间上,的图像位于函数图像的上方.……12分
满分共150分。考试时间120分钟。
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集,集合,,则
A.
B.
C.
D.
2.已知,与角终边相同的角是
A.
B.
C.
D.
3.若 ,且 ,则角是
A.第一象限角
B.第二象限角
C.第三象限角
D.第四象限角
4.若角的终边经过点,则
A.
B.
C.
D.
5.函数的定义域为
A.
B.
C.
D.
6.已知向量,那么向量的坐标是
A.
B.
C.
D.
7.函数的图像过定点
A.
B.
C.
D.
8.若,则的值为
A.
B.
C.
D.
9.设A、B、C是三角形的三个内角,下列关系恒成立的是
A.
B.
C.
D.
10.已知向量,满足,且则与的夹角为
A.
B.
C.
D.
11. 要得到的图象只需将的图象
A.向左平移个单位
B.向右平移个单位
C.向右平移个单位
D.向左平移个单位
12.已知函数是定义在上的偶函数,且在区间上单调递增,若实数满足,则的取值范围是
A.
B.
C.
D.
二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在题中横线上.
13.不等式的解集为____ ___.
14.已知,则______.
15.已知向量,若,则_____;若,则_____.
16.已知是圆上两点,弧度,,则劣弧长度是__ ____.
17.已知,则大小关系是_____ __.
18.设函数,若对任意,存在x1,x2使恒成立,则的最小值是_______.
三、解答题:本大题共6小题,共60分. 解答应写出文字说明,证明过程或演算步骤 .
19.(本题8分)求下列各式的植:
(Ⅰ);
(Ⅱ) .
解:
20.(本题8分)设全集为,集合,.
(Ⅰ)若,求;
(Ⅱ)若,求实数的取值范围.
解:
21.(本题10分)设函数.
(Ⅰ)求函数的定义域;
(Ⅱ)已知,且,求的值.
解:
22.(本题10分)已知函数.
(Ⅰ)求的最小正周期;
(Ⅱ)求函数的单调减区间;
(Ⅲ)当时,求函数的最小值.
解:
23.(本题12分)如图,点是以为直径的圆上动点,是点关于的对称点,.
(Ⅰ)当点是弧上靠近点的三等分点时,求的值;
(Ⅱ)求的最大值和最小值.
解:
24.(本题12分)设函数.
(Ⅰ)在区间上画出函数的图像;
(Ⅱ)当时,求证:在区间上,的图像位于函数图像的上方.
解:
延庆县2014—2015学年度第一学期期末考试参考答案
高一数学 2015.1
一、选择题(本大题共12小题,每小题5分,共60分.)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
B
C
B
D
C
C
A
B
D
A
二、填空题(本大题共6小题,每小题5分,共30分.)
13. 14. 15.; 16. 17. 18.
三、解答题:本大题共6小题,共60分. 解答应写出文字说明,证明过程或演算步骤 .
19.(本题8分)
解:(Ⅰ)原式. ………………………………4分
(Ⅱ)原式. …………………8分
20.(本题8分)
解:(Ⅰ)当时,,或,
∴. ………………………………4分
(Ⅱ)若,则,∴或,解得或.
∴实数的取值范围. …………………………………8分
21.(本题10分)
解:(Ⅰ)要使函数有意义,只要使,
∴函数的定义域为且. ………………3分
(Ⅱ)由,得,∴. …………5分
∵,∴. ………………7分
∴
. ………………10分
22.(本题10分)
解:(Ⅰ)∵
, ……………………2分
∴的最小正周期. ……………………4分
(Ⅱ)由得
∴函数的单调减区间. …………………7分
(Ⅲ)由.
∴当时,即时,取得最小值. …………10分
23.(本题12分)
解法一:(Ⅰ)连接,,
∵是弧靠近点的三等分点,
∴. ……………………2分
∴ ………………………4分
(Ⅱ)设, 则,
此时向量与的夹角为, ………………………6分
∴
, ………………………10分
∴ 当时,的最小值为.
当时,的最大值为. ………………12分
解法二:(Ⅰ)以直径所在直线为轴,以为坐标原点建立平面直角坐标系.
∵是弧靠近点的三等分点,连接,则, …………1分
∴点坐标为. …………2分
又点坐标是,点坐标是,
∴,,
∴. …………4分
(Ⅱ)设,,则,
∴,. ………………6分
∴
. ………10分
当时,有最小值,
当时,有最大值. …………………12分
24.(本题12分)
解]:(Ⅰ)
…………………………3分
(Ⅱ)当时,.
, ………………………5分
∵ ,∴. ………………………6分
① 当,即时,取,
.
∵ ,∴ 则.………9分
② 当,即时,取,=.
由 ①、②可知,当时,在上,
∴在区间上,的图像位于函数图像的上方.……12分
同课章节目录
