运用公式法进行因式分解(平方差)
图片预览




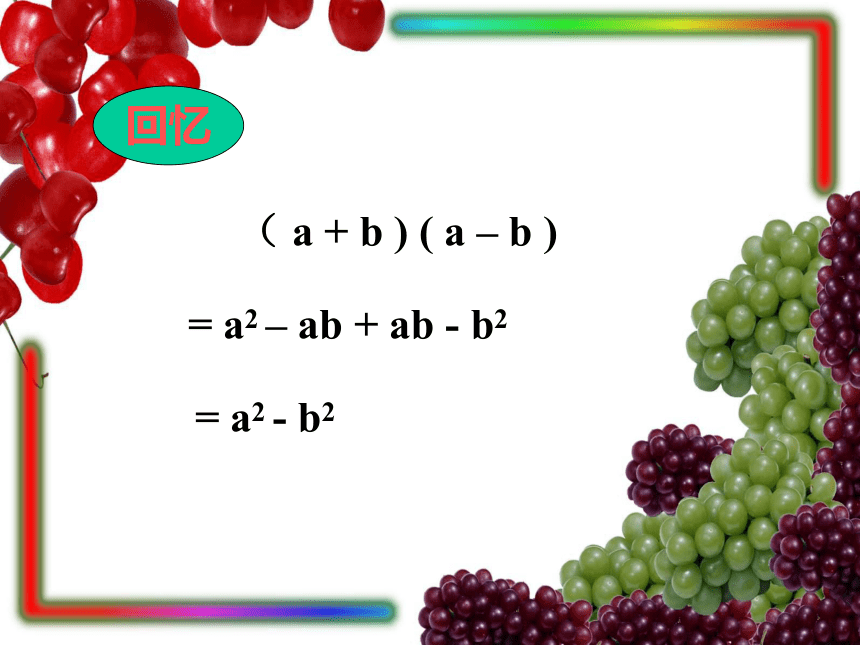






文档简介
课件30张PPT。运用公式法进行因式分解华师版《数学》八年级上因式分解(公式法)教学目标,重点难点新课导入掌握平方差公式典型例题讲解换元思想的应用课堂练习小结,布置作业教学目标1 能运用公式将简单的多项式进行分解。2 能初步接受和掌握换元思想,分解较为复杂的多项式重点掌握平方差公式难点平方差公式和换元思想的应用我们知道,整式乘法与因式分解相反,因此,利用整式乘法与因式分解的这种关系,可以得到因式分解的方法.如果把乘法公式反过来,就可以用来把某些多项式分解因式,这种分解因式的方法叫做运用公式法.回忆( a + b ) ( a – b )= a2 – ab + ab - b2= a2 - b2反过来,就得到:a2 - b2 = ( a + b ) ( a – b )也就是说,两个数的平方差,等于这两个数的和与这两个数的差的积。这个公式就是平方差公式。看两个例子:
(1) x2 - 16
(2) 9m2 - 4n2能否将这两个多项式进行因式分解。显然,在以上两个多项式中,不能找到公因式,因此不能使用提公因式法进行分解。但是通过观察我们能够发现,两个多项式都能够写成平方差的形式,由此我们可以利用刚才学习的平方差公式进行分解。(1) x2 - 16
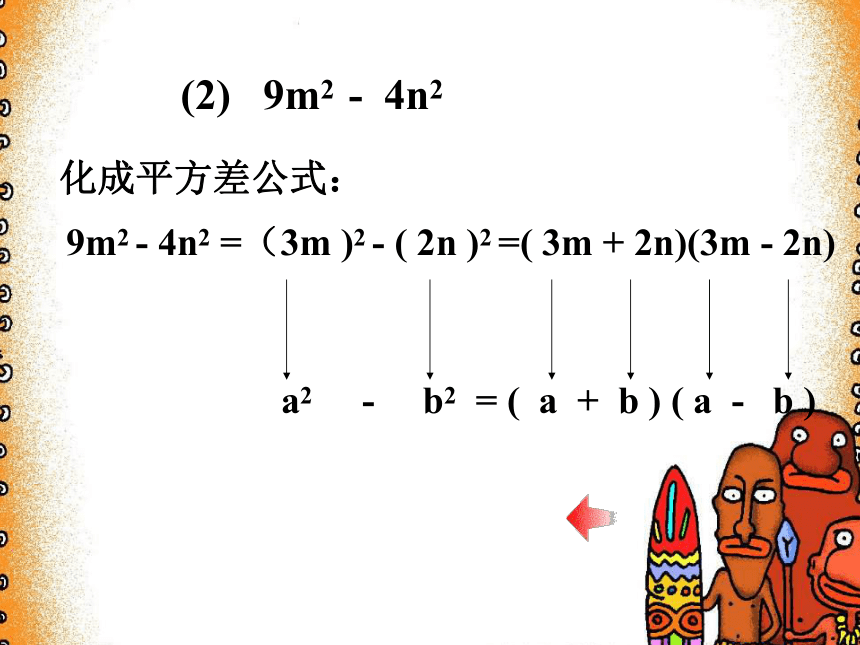
(2) 9m2 - 4n2 要用平方差公式把 x2 - 16 分解因式,只要 x2 - 16 具有平方差的形式。因为16 = 42,所以 x2 - 16=x2 - 42,它是 x 与 4 的平方差。既然 x2 - 16 确实具有平方差的形式,那么就能够运用平方差公式来分解 (1) x2 - 16分析:(1) x2 - 16x2 - 16 = x2 - 42 =( x + 4 ) ( x – 4 )a2 - b2 =( a + b ) ( a - b )利用平方差公式:(2) 9m2 - 4n2分析:因为9m2 = ( 3m )2,4n2 = ( 2n )2,所以9m2-4n2=(3m)2-(2n)2,而(3m)2-(2n)2是m与2n的平方差,那么它能够运用平方差公式来分解因式(2) 9m2 - 4n2化成平方差公式:9m2 - 4n2 =(3m )2 - ( 2n )2 =( 3m + 2n)(3m - 2n)a2 - b2 = ( a + b ) ( a - b )注意:平方差公式中的字母a,b不仅可以代表数,而且可以代表代数式。例如,第(2)题中,利用a2 - b2 =( a + b ) ( a - b )分解因式时,其中a表示3m,b表示2n
例1(1) 1 - 25b2(2) x2y2 - z2(3) 0.25m2 - 0.01n2 (1) 1 - 25b2解: 原式= 12 - ( 5b )2a2 - b2根据平方差公式得:原式=( 1 + 5b )( 1 - 5b )(2) x2y2 - z2解: 原式= (xy)2 - z2 a2 - b2根据平方差公式得:原式=( xy + z )( xy - z )(3) 0.25m2 - 0.01n2解: 原式= (0.5m)2- ( 0.1n )2 a2 - b2 根据平方差公式得:原式=( 0.5m + 0.1n )( 0.5m – 0.1n )例2(1) ( x + p )2 - ( x + q )2(2) 16(a-b)2-9(a+b)2(3) ( a + b + c )2 - ( a – b – c )2 (1) ( x + p )2 - ( x + q )2分析:(x+p)2-(x+q)2是x+p与x+q的平方差;,所以能够运用平方差公式分解因式。所以,原式=[(x+p)+(x+q)][(x+p)-(x+q)]=(2x+p+q)(p-q)(2) 16(a-b)2-9(a+b)2分析:把式子16(a-b)2-9(a+b)2改写成[4(a-b)]2-[3(a+b)]2后,可以看出它是4(a-b)与3(a+b)的平方差,所以能够运用平方差公式分解因式。
所以,原式=[4(a–b)+3(a+b)][4(a-b)-3(a+b)]=(7a-b)(a-7b)(3) ( a + b + c )2 - ( a – b – c )2根据平方差公式可以分解为:原式=[(a+b+c)+(a-b-c)][(a+b+c)-(a-b-c)]=2a(2b+2c)=4a(b+c)例3(1) x5 - x3(2) x4 - y4(1) x5 - x3解:原式= x3x2 - x3= x3 ( x 2- 1 )= x3 ( x + 1 ) ( x – 1 )(2) x4 - y4解:原式= ( x2 )2 - ( y2 )2=( x2 + y2 )( x2 - y2 )=( x2 + y2 ) ( x + y ) ( x - y )注意:(1)如果多项式各项有公因式,那么先提公因式,再进一步分解 。(2)因式分解,必须进行到每个多项式因式不能分解为止.
课堂练习:(1) a2 - 0.25x2 (2) 36 - m2
(3) 4x2 - 9y2 (4) 0.81a2 - 16b2
(5) 36n2 - 1 (6) 25p2 - 49q2
(7)4a2 - ( b + c )2 (8) (3m+2n)2-(m-n)2课堂小结 1 多项式各项有公因式时, 应先提取公因式,然后考虑运用公式法2 注意变号3 提取某一项后,“1”不能省略4 负号提前回家作业(1) a2 - 49 (2) 64 - x2
(3) 1 - 36b2 (4) m2 - 81n2
(5)0.49p2-144q2 (6) 121x2-4y2
(7) (m+n)2-n2 (8) (x2+y2)2-x2y2
(1) x2 - 16
(2) 9m2 - 4n2能否将这两个多项式进行因式分解。显然,在以上两个多项式中,不能找到公因式,因此不能使用提公因式法进行分解。但是通过观察我们能够发现,两个多项式都能够写成平方差的形式,由此我们可以利用刚才学习的平方差公式进行分解。(1) x2 - 16
(2) 9m2 - 4n2 要用平方差公式把 x2 - 16 分解因式,只要 x2 - 16 具有平方差的形式。因为16 = 42,所以 x2 - 16=x2 - 42,它是 x 与 4 的平方差。既然 x2 - 16 确实具有平方差的形式,那么就能够运用平方差公式来分解 (1) x2 - 16分析:(1) x2 - 16x2 - 16 = x2 - 42 =( x + 4 ) ( x – 4 )a2 - b2 =( a + b ) ( a - b )利用平方差公式:(2) 9m2 - 4n2分析:因为9m2 = ( 3m )2,4n2 = ( 2n )2,所以9m2-4n2=(3m)2-(2n)2,而(3m)2-(2n)2是m与2n的平方差,那么它能够运用平方差公式来分解因式(2) 9m2 - 4n2化成平方差公式:9m2 - 4n2 =(3m )2 - ( 2n )2 =( 3m + 2n)(3m - 2n)a2 - b2 = ( a + b ) ( a - b )注意:平方差公式中的字母a,b不仅可以代表数,而且可以代表代数式。例如,第(2)题中,利用a2 - b2 =( a + b ) ( a - b )分解因式时,其中a表示3m,b表示2n
例1(1) 1 - 25b2(2) x2y2 - z2(3) 0.25m2 - 0.01n2 (1) 1 - 25b2解: 原式= 12 - ( 5b )2a2 - b2根据平方差公式得:原式=( 1 + 5b )( 1 - 5b )(2) x2y2 - z2解: 原式= (xy)2 - z2 a2 - b2根据平方差公式得:原式=( xy + z )( xy - z )(3) 0.25m2 - 0.01n2解: 原式= (0.5m)2- ( 0.1n )2 a2 - b2 根据平方差公式得:原式=( 0.5m + 0.1n )( 0.5m – 0.1n )例2(1) ( x + p )2 - ( x + q )2(2) 16(a-b)2-9(a+b)2(3) ( a + b + c )2 - ( a – b – c )2 (1) ( x + p )2 - ( x + q )2分析:(x+p)2-(x+q)2是x+p与x+q的平方差;,所以能够运用平方差公式分解因式。所以,原式=[(x+p)+(x+q)][(x+p)-(x+q)]=(2x+p+q)(p-q)(2) 16(a-b)2-9(a+b)2分析:把式子16(a-b)2-9(a+b)2改写成[4(a-b)]2-[3(a+b)]2后,可以看出它是4(a-b)与3(a+b)的平方差,所以能够运用平方差公式分解因式。
所以,原式=[4(a–b)+3(a+b)][4(a-b)-3(a+b)]=(7a-b)(a-7b)(3) ( a + b + c )2 - ( a – b – c )2根据平方差公式可以分解为:原式=[(a+b+c)+(a-b-c)][(a+b+c)-(a-b-c)]=2a(2b+2c)=4a(b+c)例3(1) x5 - x3(2) x4 - y4(1) x5 - x3解:原式= x3x2 - x3= x3 ( x 2- 1 )= x3 ( x + 1 ) ( x – 1 )(2) x4 - y4解:原式= ( x2 )2 - ( y2 )2=( x2 + y2 )( x2 - y2 )=( x2 + y2 ) ( x + y ) ( x - y )注意:(1)如果多项式各项有公因式,那么先提公因式,再进一步分解 。(2)因式分解,必须进行到每个多项式因式不能分解为止.
课堂练习:(1) a2 - 0.25x2 (2) 36 - m2
(3) 4x2 - 9y2 (4) 0.81a2 - 16b2
(5) 36n2 - 1 (6) 25p2 - 49q2
(7)4a2 - ( b + c )2 (8) (3m+2n)2-(m-n)2课堂小结 1 多项式各项有公因式时, 应先提取公因式,然后考虑运用公式法2 注意变号3 提取某一项后,“1”不能省略4 负号提前回家作业(1) a2 - 49 (2) 64 - x2
(3) 1 - 36b2 (4) m2 - 81n2
(5)0.49p2-144q2 (6) 121x2-4y2
(7) (m+n)2-n2 (8) (x2+y2)2-x2y2
